Klimatrends in Temperaturreihen

1. Was ist Persistenz in Temperaturzeitreihen?
Zeitreihen sind wichtige Werkzeuge, um Informationen über komplexe Prozesse zu gewinnen. Herzspezialisten nehmen Zeitreihen des Herzschlags oder des Blutdrucks auf, um Aufschlüsse über den gesundheitlichen Zustand eines Patienten zu erhalten. Finanz- und Versicherungsmathematiker analysieren Zeitreihen, um die finanziellen oder versicherungstechnischen Risken von Unternehmen zu bewerten. Klimatologen verwenden Temperaturzeitreihen (Tages-, Monats- oder Jahresmittelwerte), um langfristige Klimatrends aufzufinden. Im Folgenden geht es hier um Temperaturzeitreihen.
Der englische Wasserbau-Ingenieur Harold Edwin Hurst untersuchte in den 1950-er Jahren  die Tief- und Höchststände des Nils und entdeckte dabei als erster, dass hydrologische Zeitreihen ein Gedächtnis besitzen. Die aktuell gemessenen Werte hängen von den vergangenen, zum Teil weit zurückliegenden Werten ab. Später wurde erkannt, dass auch viele weitere Zeitreihen der Natur wie z.B. Baumringe ein Gedächtnis aufweisen. Man nennt dieses Phänomen Persistenz oder Autokorrelation. Die Schwankungen der Zeitreihe um ihren Mittelwert erfolgen in persistenten Zeitreihen nicht mehr unabhängig, sondern sie werden von der Vergangenheit der Zeitreihe beeinflusst.
Betrachtet man Temperaturzeitreihen, so erscheint dieses Verhalten zunächst nicht einmal so ungewöhnlich. Eine Temperaturzeitreihe weist zumindest ein "Gedächtnis" über die momentan herrschende Jahreszeit auf. Es kommt nie vor, dass auf einen warmen Sommertag plötzlich ein kalter Wintertag folgt, bzw. umgekehrt. Da jahreszeitlich bedingte Schwankungen im Allgemeinen weniger interessieren, werden die saisonalen Einflüsse vor der Persistenzanalyse aus einer Temperaturzeitreihe entfernt. Aber auch danach beobachtet man noch, dass ein Tagestemperaturmittelwert zumindest vom Vortag abhängt. So wird ein über dem längerfristigen Mittel liegender Temperaturwert am nächsten Tag mit über 50% Wahrscheinlichkeit ebenfalls über diesem Mittel liegen, Entsprechendes trifft für einen unter dem Mittel liegenden Temperaturwert zu. Eine Erklärung für dieses Phänomen liefern anhaltende Wetterlagen. Persistenz über mehrere Wochen kann man mit meteorologischen Blocksituationen, wie etwa einem lang anhaltendes Azorenhoch erklären. Für noch längere Zeiträume ist freilich über die Ursachen von Persistenz wenig bekannt. Es werden dekadale Oszillationen wie z.B. der El Nino, Einflüsse aus den sich ändernden Planetenkonstellationen und weiteres mehr diskutiert. Erstaunlicherweise findet man in Temperaturzeitreihen Persistenz bis über mehrere Jahrzehnte. Die Ursachen solch langreichweitiger Persistenz sind bis heute völlig unbekannt.
Persistenz in Temperaturzeitreihen kann bemerkenswerterweise empirisch mit nur einem Parameter beschrieben werden, dem berühmten Hurst-Exponenten alpha. Mit der Fluktuationsanalyse (FA) bzw. der auf der FA aufbauenden, trendbereinigten Fluktuationsanalyse (DFA) wird alpha ermittelt. Der hier interessierende Bereich von alpha in Temperaturreihen ist 0,5 ≤ alpha < 1. Eine Zeitreihe mit alpha = 0,5 ist rein zufällig (weißes Rauschen) und besitzt keine Persistenz . Für alpha > 1 (alpha ≈ 1 entspricht rotem Rauschen) wird die Zeitreihe instationär, ihre Werte können "weglaufen" und niemals wieder den Anfangswert erreichen. Stationäre Zeitreihen behalten dagegen ihren Mittelwert über längere Zeiten bei. Gemessene Temperaturzeitreihen sind stationär, ihre Hurst-Exponenten liegen deutlich unter alpha = 1. Nur fragwürdige Homogenisierungen [22], Glättungsprozeduren oder ähnliche Manipulationen können dies ändern. Die Hurst-Exponenten von sorgfältig gemessenen Temperaturzeitreihen, bei denen nur die unbedingt notwendigen Homogenisierungen vorgenommen wurden, bewegen sich im Bereich von etwa 0,55 bis 0,65. Temperaturzeitreihen von Stationen auf Inseln oder in Meeresnähe weisen höhere alpha-Werte bis maximal etwa 0,9 auf.
2. Persistenz, Trends und Extreme
Persistenz von Temperaturzeitreihen sieht zuerst wie eine mathematische Rarität aus, tatsächlich ist sie jedoch von maßgebender Relevanz. Die Analyse von Zeitreihen ist nämlich vorrangig an dem Auftreten von Trends sowie von Extremen interessiert. Dabei hat man die Vorstellung, dass ausgeprägte Trends oder Extreme durch äußere Einflüsse bedingt sind. Tatsächlich kommen aber extreme Temperaturanstiege bzw. -abfälle oder ungewöhnlich lange Serien von Jahren mit Maximaltemperaturen bzw. Minimaltemperaturen auch ohne äußere Einflüsse vor. Ist dies der Fall, sind diese Trends oder Extreme "natürlich". Zumindest von stark ausgeprägten Extremen vermutet man freilich, dass sie unnatürlich sind. d.h. durch externe Einflüsse erzeugt wurden. Diese unzutreffende Annahme ist aus der Erfahrung täglichen Lebens abgeleitet. Ein Würfelspieler freut sich darüber, wenn die von ihm bevorzugte Zahl in Serie erscheint. Ist die Serie allerdings ungewöhnlich lang oder kommen gar solche Serien ungewöhnlich oft vor, argwöhnt man zutreffend eine externe Ursache, einen „gezinkten“ Würfel oder betrügerische Manipulation. Für Temperaturzeitreihen geht diese intuitive Beurteilung allerdings fehl. Der Grund dafür ist Persistenz.
Die entscheidende Folge von Persistenz in Zeitreihen ist, dass ausgeprägte Trends und Extreme auf natürliche Weise mit zunehmender Persistenzstärke ebenfalls zunehmen.

Diese Folge von Persistenz ist anschaulich verständlich. Persistenz bewirkt, dass die Zeitreihe die Tendenz aufweist, einen einmal angenommenen Wert beizubehalten. Auf diese Weise entstehen mehr Extreme und längere Trends. Damit wird der Stellenwert von Persistenz für Temperaturzeitreihen-Analye deutlich. Finden wir beispielsweise in einer Temperaturzeitreihe des 20. Jahrhunderts einen Erwärmungstrend, so besagt dies keineswegs zwingend, dass hierfür eine unnatürliche Ursache, wie z.B. zunehmendes CO2 oder Stadterwärmung (UHI) verantwortlich sein muss. Der Trend könnte auch eine ganz natürliche Folge der Persistenz der Zeitreihe sein.
Vor näherem Eingehen auf  Persistenz in Temperaturreihen soll zur Veranschaulichung des Phänomens gezeigt werden, wie man einem Würfel zu Persistenz verhelfen kann. Ein solcher Persistenzwürfel wird deutlich mehr Trends in Form von ungewöhnlich langen Serien gleicher Augenzahlen liefern. Dennoch bleibt er „fair“, d.h. alle Augenzahlen kommen auf Dauer gleich oft vor. Der Persistenzwürfel ist ein gewöhnlicher Würfel mit einer Besonderheit: wird er geworfen, und es erscheint beispielsweise die 5, hängt der Spieler ein kleines Gewicht an die gegenüberliegende Seite, also an die 2. Dies erhöht die Wahrscheinlichkeit, dass auch weiterhin die 5 gewürfelt wird. Dennoch wird irgendwann eine andere Zahl auftauchen. Nun hängt der Spieler das Gewicht auf deren Unterseite. Würfelt man lange genug, kommen alle Augen mit gleicher Wahrscheinlichkeit vor. Dennoch erscheinen ungewöhnlich lange Serien von jeweils gleicher Augenzahl. Sie sind jedoch nur durch das zum System gehörige Gewicht bestimmt, nicht durch äußere Einflüsse (man kann sich den Mechanismus intern gesteuert vorstellen, ein Spieler, der die Gewichte anbringt, ist prinzipiell unnötig). Die langen Serien gleicher Zahlen treten rein zufällig auf und sind völlig natürlich.
Im Gegensatz zu Temperaturreihen reicht das Gedächtnis des Persistenzwürfels allerdings nur einen einzigen Wurf zurück. Man kann dieses Verhalten mit einem sog. AR(1) Prozess modellieren. Persistenz in Temperaturreihen hat dagegen mit Modellprozessen, wie in AR-, MA- oder ARMA-Modellen [13] nichts zu tun. Persistenz ist eine empirische Eigenschaft ohne Modellgrundlage und sie ist prinzipiell beliebig langreichweitig. Man kann mit dem Computer synthetische Zufallszeitreihen erzeugen, die eine vorgegebene Persistenz, d.h. einen vorgegebenen Hurst-Exponenten alpha aufweisen [1]. Mit Hilfe solcher Surrogatreihen lassen sich die durch Persistenz entstehenden Phänomene studieren.
3. Surrogatzeitreihen mit „Gedächtnis“
Surrogatzeitreihen, d.h. mit dem Computer erzeugte künstliche Zeitreihen, die zudem Persistenz aufweisen, sind ein entscheidendes Hilfsmittel zur Persistenzanalyse. Die Erzeugung von rechteckverteilten Zufallszahlen (Pseudozufallszahlen) mit dem Computer ist jedem EXCEL-Benutzer bekannt. Bildet man solche Zufallszahlen auf den Bereich von Jahresmitteltemperaturen ab, erhält man eine Temperaturzeitreihe mit dem Hurst-Exponenten von alpha = 0,5. Eine solche Reihe sieht freilich unrealistisch aus, sie entspricht bereits dem Augenschein nach noch nicht der Gestalt einer real gemessenen Temperaturzeitreihe.
Surrogatreihen werden „lebensechter“, wenn man ihnen zu Persistenz verhilft. Zur Veranschaulichung sei an das oben beschriebene Beispiel des Persistenzwürfels erinnert. Die Vermittelung von Persistenz an eine Temperaturzeitreihe erfolgt allerdings mit dem Computer – Details finden sich in der Originalliteratur [1], [24]. Surrogatreihen des gleichen alpha wie eine gemessene reale Reihe, weisen schon beim bloßen Anschauen eine große Ähnlichkeit mit  gemessenen Reihen auf. Allerdings können reale Temperaturreihen einen externen Trend enthalten, Surrogatreihen nicht. Man könnte Surrogatreihen daher zutreffend als „natürlich“ bezeichnen, obwohl diese Bezeichnung etwas paradox erscheint, denn sie wurden schließlich vom Computer erzeugt. In konsequent gleichem Sprachgebrauch sind reale Temperaturreihen mit einem externen Trend „unnatürlich“. 
Bild 1 (s. Titelbild oben) zeigt ein Anschauungsbeispiel, wie sich Persistenz in Surrogatreihen auswirken kann: Im linken Teilbild ist eine ausgewählte Zeitreihe mit alpha = 0,5 (keine Persistenz) gezeigt, im rechten Teilbild eine von alpha = 0,73. Beide Zeitreihen sind Surrogate und enthalten keinen externen Trend. Dennoch ist im rechten Teilbild deutlich ein „Trend“ erkennbar, der ein wenig an den Verlauf der globalen Erwärmung im 20. Jahrhundert erinnert. Er ist rein zufällig, natürlich und nur durch Persistenz bedingt. Nun entsteht die wichtige Frage: Woher erkennt man im konkreten Fall, ob ein Trend in einer real gemessenen Temperaturreihe extern ist?
4. Die Suche nach externen  Trends
Externe Trends in Temperaturreihen stehen zweifellos im Mittelpunkt der heutigen Klimadiskussion. So möchte man gerne wissen, ob die in den letzten Jahrzehnten des 20. Jahrhunderts von vielen Stationen gemessene globale Erwärmung ein vom industrialisierten Menschen verantworteter Trend oder aber nur ein durch Persistenz bedingter Artefakt ist. In diesem Zusammenhang ist zu betonen, dass die von den weltweit verstreuten Stationen gemessene Erwärmung im 20. Jahrhundert keinesfalls global einheitlich ausfällt.  Etwa ein Viertel aller Stationen zeigt in diesem Zeitraum nämlich Abkühlung [6], [12]. Die mathematischen Hilfsmittel zur Persistenzanalyse von Temperaturreihen liefern die schon erwähnten Methoden der FA und der DFA. Eine ausführliche Beschreibung dieser Verfahren findet sich in [2], hier werden insbesondere auch sämtliche Originalliteraturquellen bis zum Jahre 2004 aufgeführt. Auf der Webseite von em. Prof. Bunde (Univ. Gießen) sind viele Originalpaper zur Persistenzanalyse, auf denen er als Mit- oder Hauptautor zeichnete, als pdf abgreifbar [23]. In [6] finden sich ebenfalls Literaturquellen. Schlussendlich ist der ausführliche und gut allgemeinverständlich gefasste Übersichtsaufsatz zur Persistenzanalyse von Bunde und Kantelhardt in den physikalischen Blättern hervorzuheben [21]. Die Originalarbeiten der hier im Mittelpunkt stehenden neuesten Methode der Persistenzanalyse, die schließlich unter 5. näher beschrieben wird, finden sich in [3] und [4].
In groben Zügen sieht die Arbeitsweise der „klassischen“ Persistenzanalye wie folgt aus: Mit der FA wird aus einer Zeitreihe der Hurst-Exponent alphaFA ermittelt. Enthält die Reihe einen externen Trend, ergibt sich ein höheres alphaFA als ohne diesen Trend. Daher liefert die FA im Prinzip nur für Zeitreihen, die keine externen Trends enthalten, unverfälschte Ergebnisse des Hurst-Exponenten. Zur Behebung dieses Mangels wurde die DFA entwickelt. Sie beseitigt während des Berechnungsvorgangs automatisch polynominale Trends einer vorgegebenen Ordnung aus der Zeitreihe. Zur Vereinfachung beschränkt man sich hierbei meist auf die Beseitigung von linearen Trends. Wird mit der DFA überhaupt kein Trend entfernt, liegt wieder die FA vor. Mit der DFA kann der automatisch beseitigte Trend leider nicht explizit angegeben werden. Da der Hurst-Exponent der DFA alphaDFA ist naturgemäß stets größer als der der FA alphaFA, kann die Differenz (alühaDFA – alphaFA) als Stärke des externen Trends in der analysierten Temperaturreihe angesehen werden.
Bild 2 zeigt als Beispiel die Ergebnisse von FA- und DFA-Analysen (Beseitigung von linearen Trends) der Monatsmittelwertreihen von fünf der am weitesten bis ins 18. Jahrhundert zurückreichenden europäischen Wetterstationen.

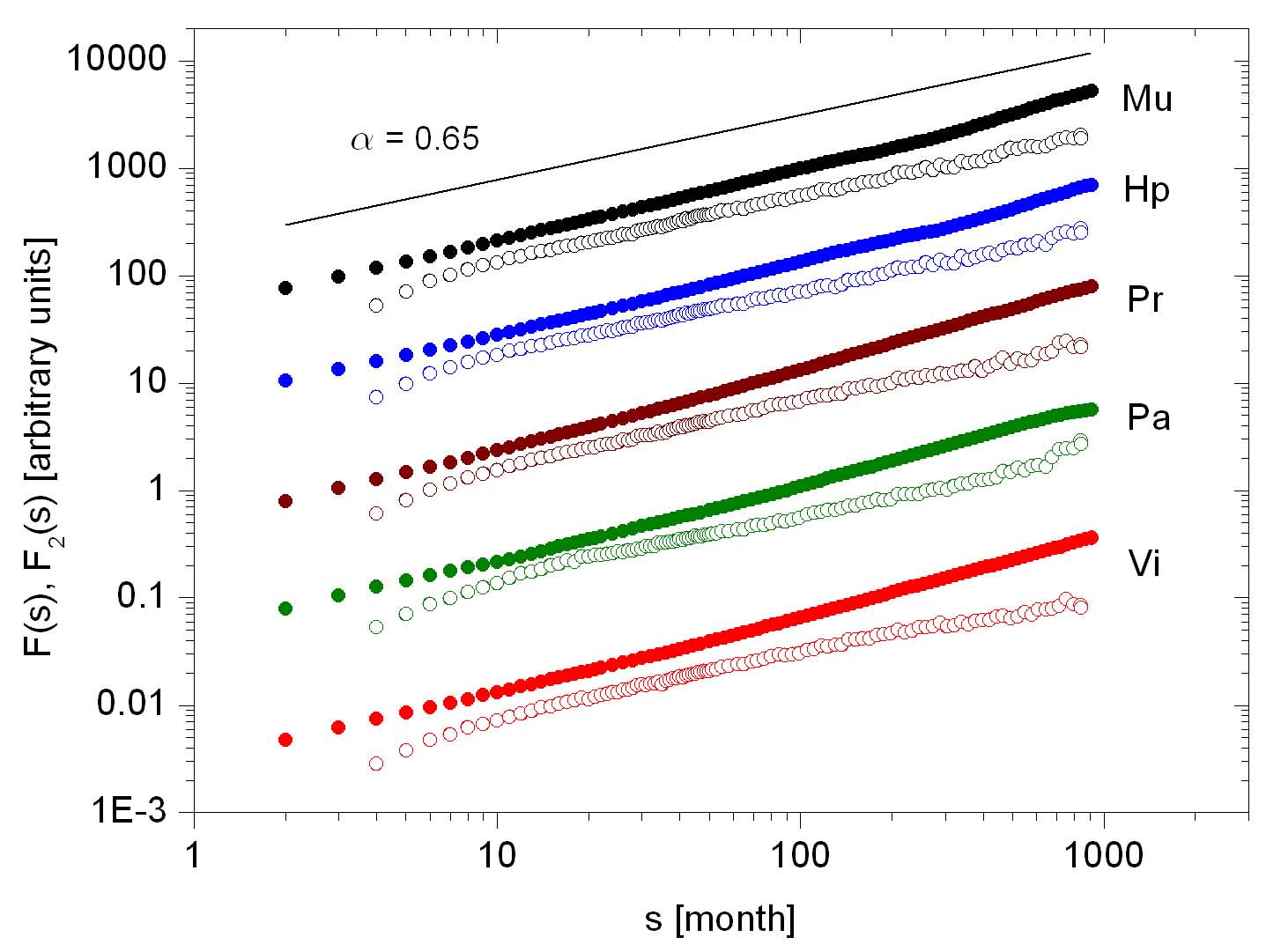
Bild 2: FA-Analyse (gefüllte Kreise) und DFA-Analyse (offene Kreise) für die Stationen München, Hohenpeissenberg, Prag, Paris und Wien . Die Länge des betrachteten Zeitraums beträgt 1791 bis zum Jahr 2000. Man erhält Hurst-Exponenten zwischen 0,52 und 0,63 aus der DFA- und 0,63-0,71 aus der FA-Analyse.

Aus den Monatsreihen wurde, wie bereits beschrieben, der saisonale Jahresgang entfernt. Ein doppelt-logarithmischer Plot erlaubt es dann, direkt aus der Steigung der charakteristischen Größe F(s) den Hurst-Exponenten a abzulesen [2]. Die Hurst-Exponenten der FA sind, wie schon erwähnt, im Prinzip größer als die der DFA. Für unser Beispiel in Bild 2 folgt daraus, dass alle fünf Reihen (lineare) Trends enthalten. Die Frage, ob diese Trends unnatürlich sind, oder ob sie durch Persistenz entstanden sind, kann nicht ohne weiteres beantwortet werden. Allerdings fällt im vorliegenden Fall die Entscheidung leicht, weil alle fünf Reihen aus nicht allzu weit voneinander entfernten Stationen stammen, einen sehr ähnlichen Verlauf und schließlich auch ähnliche alpha-Werte aufweisen. Somit liegt mit hoher Wahrscheinlichkeit tatsächlich ein externer Trend vor.
Erst die in jüngster Zeit entwickelte Methode von Lennartz und Bunde, die nachfolgend beschrieben wird, kann dann die wichtige Frage nach der Unnatürlichkeit eines gemessenen Trends in einer einzelnen Temperaturzeitreihe quantitativ beantworten.

5. Die Methode von Lennartz und Bunde
Bis zum Jahre 2009 ergab für eine Temperaturzeitreihe nur der Vergleich ihrer beiden Hurst-Exponenten alphaFA, alphaDFA aus der FA- und der DFA-Analyse einen Hinweis, ob ein beobachteter (linearer) Trend in ihr externen Ursprungs war. Diese einfache Strategie erlaubte freilich schon wichtige Aussagen. Sie wurde unter anderem in einer Publikation des Jahres 2003 auf 95 weltweit verstreute Temperaturzeitreihen angewendet. Dabei konnten keine Anzeichen für eine globale Erwärmung aufgefunden werden [5]. Lennartz und Bunde (im Folgenden LB) zeigten schließlich in zwei bahnbrechenden Fachaufsätzen der Jahre 2009 und 2011 [3], [4], dass eine wesentliche Erweiterung der oben beschriebenen klassischen Persistenzanalyse hin zu quantitativen Wahrscheinlichkeitsangaben möglich ist. Hierzu verwendeten sie Surrogat-Zeitreihen und untersuchten, wie häufig natürliche (lineare) Trends in ihnen vorkommen. Die maßgebende dimensionslose Größe ist dabei ∆/s. ∆ [°C] ist der Temperaturanstieg bzw. der Temperaturabfall der linearen Regressionsgeraden über die gesamte Länge der Temperaturreihe und s [°C] die Standardabweichung um die Regressionsgerade herum. ∆ ist durch die Standardabweichung zu dividieren, weil die Signifikanz eines Trends mit abnehmender Standardabweichung s zunimmt. Weist die Reihe große Schwankungen, also eine große Standardabweichung s auf, ist der Trend ∆ weniger signifikant als bei kleinem s. Im Extremfall von s = 0 ist der Trend mit dem Verlauf der Zeitreihe identisch, im entgegengesetzten Extremfall beliebig großer Standardabweichung kann bei der geringsten Änderung irgendeines Wertes der Reihe die Regressionsgerade völlig anders verlaufen.
Aus unzähligen Surrogatreihen und Computer-Rechenläufen ermittelten LB für zwei Spezialfälle, nämlich Zeitreihen der festen Längen von 50 und 100 Jahren, charakteristische Diagramme bzw. die zu diesen gehörenden empirischen Rechenformeln [3]. Aus den Diagrammen kann abgelesen werden, mit welcher kumulierten Wahrscheinlichkeit W ein linearer Trend ∆/s unnatürlich (extern) ist. Im Jahre 2011 erweiterten LB ihre Methode schließlich auf allgemeine Zeiträume von 40 bis 160 Jahren Länge [4]. Bild 3 zeigt ein solches Diagramm (vom Autor erstellt) für den Fall von Surrogatreihen von 100 Jahren Länge.

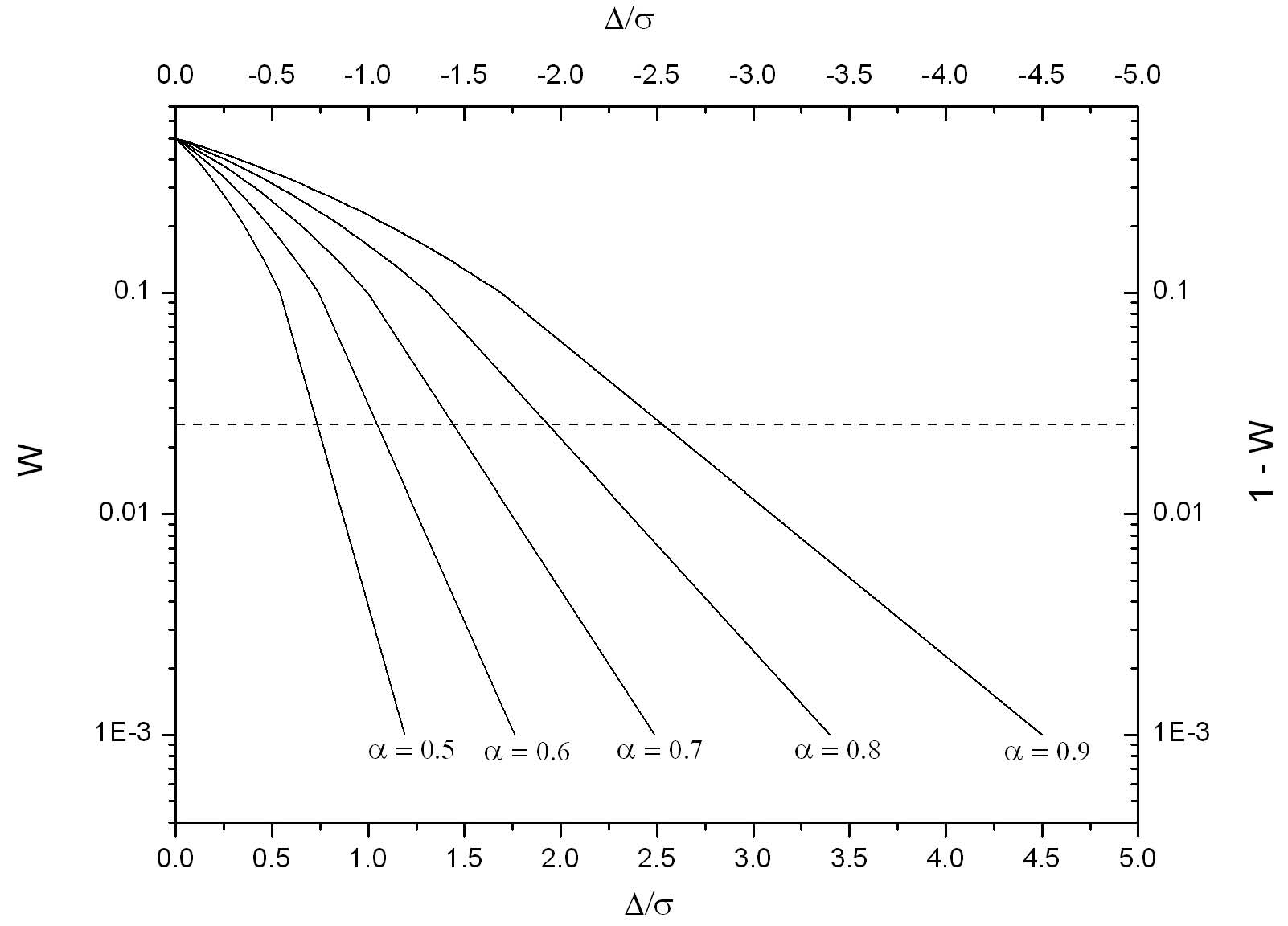
Bild 3: Kumulierte Wahrscheinlichkeit W für lineare Trends ∆/www.physik.uni-halle.de/Fachgruppen/kantel/habil.pdf
[3] S. Lennartz and A. Bunde: Trend evaluation in records with long-term memory: application to global warming, Geophys. Res. Lett., 36, L16706, doi:10.1029/2009GL039516, 2009
[4] S. Lennartz and A. Bunde: Distribution of natural trends in long-term correlated records: a scaling approach, Phys. Rev. E84, 021129, doi:10.1103/PhysRevE84.021129, 2011
[5] J.F. Eichner, E. Koscielny-Bunde, A. Bunde, S. Havlin, and H.-J. Schellnhuber: Power-law persistence and trends in the atmosphere: A detailed study of long temperature records, Phys. Rev. E68, 046133, 2003
[6] H.-J. Lüdecke, R. Link, and F.-K. Ewert: How Natural is the Recent Centennial Warming? An Analysis of 2249 Surface Temperature Records, Int. J. Mod. Phys. C, Vol. 22, No. 10, 2011, http://www.eike-klima-energie.eu/uploads/media/How_natural.pdf
[7] G. Paltridge, A. Arking, and M. Pook: Trends in middle- and upper-level tropospheric humidity from NCEP reanalysis data, Theor. Appl. Climatol., 98, p. 351-359, 2009
[8] R.W. Spencer, and W.D. Braswell: On the misdiagnosis of surface temperature feedbacks from variations in Earth’s radiant energy balance, Remote. Sens. 3, p. 1603-1613, 2011
[9] R.S. Lindzen and Y.-S. Choi: On the determination of climate feedbacks from ERBE data, Geophys. Res. Lett., 36, L16705, 2009
[10] R. Allan: Combining satellite data and models to estimate cloud radiative effect at the surface and in the atmosphere, Meteorol. Appl., 18, p. 3245-333, 2011
[11] H. Harde: How much CO2 really contributes to global warming? Spectroscopic studies and modelling of the influence of H2O, CO2 and CH4 on our climate, Geophys. Res. Abstracts, 13, EGU2011-4505-1, 2011
[12] R. Muller, BEST, Berkeley University, 2011
[13] http://de.wikipedia.org/wiki/ARMA-Modell
[14] http://judithcurry.com/2011/11/07/two-new-papers-vs-best/
[15] http://judithcurry.com/2011/11/08/tols-critique-of-the-ludecke-et-al-papers/
[16] http://judithcurry.com/2011/11/10/ludecke-et-al-respond/
[17] http://judithcurry.com/2011/11/15/ludecke-et-al-respond-part-ii/
[18] wmbriggs.com/blog/?p=4630
[19] http://www.focus.de/wissen/wissenschaft/klima/weltklimakonferenz_2011/tid-24293/weltklimakonferenz-viel-laerm-um-nichts_aid_687885.htm
[20] WUWT: http://tinyurl.com/ae342yp
[21] A. Bunde und J.W. Kantelhardt: Langzeitkorrelationen in der Natur: von Klima, Erbgut und Herzrythmus, Physikalische Blätter 57, Nr. 5, S. 49-54, 2001
[22] E. Steirou and D. Koutsoyiannis: Investigation of methods for hydroclimatic data homogenisation, European Geosciences Union General 2012, Vienna Austria 22-27 April 2012, Session HS.4/AS4.17/CL2.10, http://itia.ntua.gr/en/docinfo/1212/, 2012
[23] http://www.uni-giessen.de/cms/fbz/fb07/fachgebiete/physik/einrichtungen/theorie/institut-fur-theoretische-physik-iii/pub/paper
[24] H. Makse et al.: Method for Generating Long-Term Correlations for Large Systems, ArXiv, http://arxiv.org/abs/cond-mat/9512024