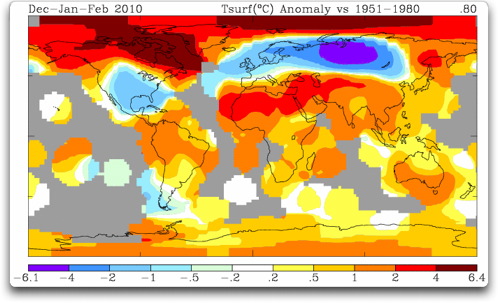
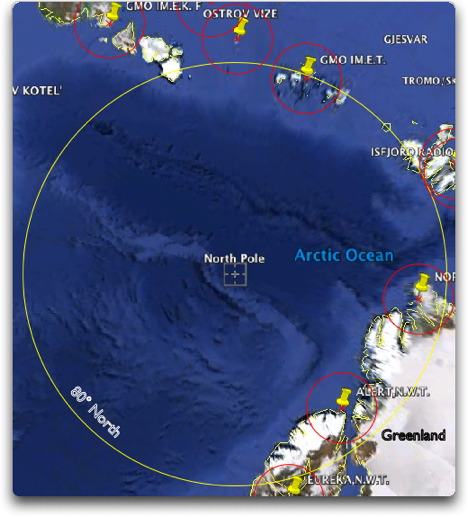
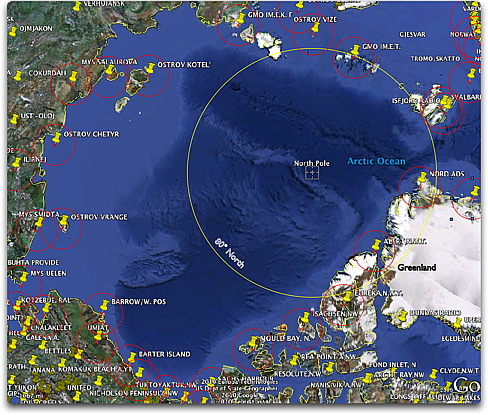
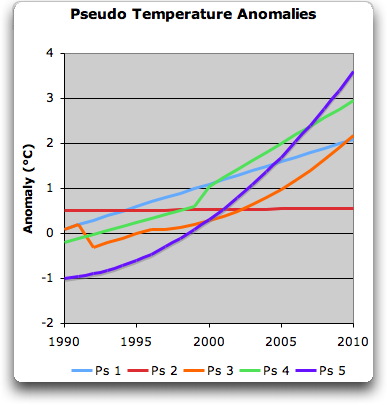
Immer wieder merkwürdige Probleme mit den IPCC Zahlen! Geschätzte Klimasensitivität deutlich zu hoch?
Ich wurde von der offensichtlich deutlichen Diskrepanz in den offiziellen IPCC-Zahlen überrascht. Der IPCC-Schätzwert der Klimasensitivität ist +3 [+2 bis +4.5] °C pro Verdoppelung.
Wir haben auch die IPCC-Abschätzung der Veränderungen beim Antrieb seit 1750 in Watt/m2. Der menschliche Beitrag zu diesem Antrieb wird im 2007er IPCC "Summary for Policymakers" wie folgt angegeben:
Das Verständnis der anthropogenen Erwärmungs- und Abkühlungswirkungen auf das Klima ist seit dem Dritten Auswertebericht (Third Assessment Report – TAR) besser geworden und hat zu einer sehr hohen Zuversicht geführt, dass der global gemittelte Netto-Effekt der menschlichen Aktivität seit 1750 eine Erwärmung bewirkte wobei der Strahlungsantrieb + 1,6 [+0.6 to +2.4] W/m2 betrug.
Das stellt die bestmögliche Abschätzung dar [innerhalb der unteren und oberen Grenze].
Jetzt wird aber vom IPCC für eine Verdoppelung des CO2 eine Veränderung des Strahlungsantriebs um 3,7 W/m2 angegeben. Wenn wir also die Klimasensitivität (in Grad pro Verdoppelung) durch 3,7 dividieren, erhalten wir die Klimasensitivität in Grad/m2 ausgedrückt. Ergebnis:
Klimasensitivität = +0.8 [+0.5 bis +1.2] Grad pro W/m2.
Schließlich wissen wir, dass Sensitivität mal Veränderung des Antriebs die Temperaturveränderung ergibt. Wenn wir die IPCC-Schätzwerte benutzen, erhalten wir:
+0.8 [+0.5 bis +1.2] Grad pro W/m2 mal +1.6 [+0.6 to +2.4] W/m2
= +1.3 [+0.4 to +2.2] Grad Erwärmung aus menschlicher Aktivität seit 1750. (Durchlaufende Fehler sind als quadratisch additiv angenommen.)
Für die Zeit vor 1850 haben wir keine guten Temperaturdaten, also müssen wir das berücksichtigen. Es gab aber auch nur einen sehr geringen menschlichen Einfluss auf das Klima zwischen 1750 bis 1850. Die CO2-Pegel waren 1750 nur geringfügig niedriger als 1850, die industrielle Revolution steckte noch in den Kinderschuhen, fossile Treibstoffe wurden kaum verbrannt, Schwefelemissionen vernachlässigbar gering, Fluorkohlenstoff wurde nicht emittiert. Weil der menschliche Beitrag zwischen 1750 – 1850 sehr gering ist im Vergleich zum gesamten menschenverursachten Antrieb, hat das IPCC für das Ausmaß der anthropogenen Temperaturänderung für die Zeit nach 1850 als besten Schätzwert +1.3 Grad [+0.4 bis +2.2 für die untere und obere Grenze] angesetzt.
Um zu einer abschließenden Schätzung zu gelangen, müssen wir die natürlichen Antriebe seit 1850 zu den anthropogenen Antrieben hinzurechnen. Das IPCC berücksichtigt nur einen davon, den Sonnenantrieb. Es schätzt den Sonnenantrieb während der rund 250 Jahre seit 1750 auf 0,12 W/m2. Für unsere abschlägigen Rechnungen können wir in grober, aber passender Schätzung annehmen, dass drei Fünftel der Veränderungen seit 1850 stattfanden. Wenn man den Sonnenantrieb den vorherigen Berechnungen hinzufügt, dann erhöht sich die Temperaturänderung aus anthropogenen und natürlichen Antrieben zusammen seit 1850 leicht nach oben, auf +1.4 [+0.4 to +2.3] Grad.
Darin liegt aber ein Problem, ein großes sogar. Der HadCRUT Datenbasis zufolge [monatliche Daten hier, mit Bemerkungen hier], beträgt die gesamte Temperaturänderung 1850 – 2006 +0.7 [+0.5 to +0.9] Grad. Mit anderen Worten, die Erde hat sich seit 1850 um etwa drei Viertel eines Grades erwärmt (beste Schätzung 0,7 C0 ). Das ist weit entfernt von 2,3 C0, dem oberen Ende dessen, was das IPCC für das Geschehen nach 1850 angibt. Es ist nur die Hälfte von den höchstwahrscheinlichen Werten, die das IPCC angibt. Es ist gerade mal über dem unteren Rand der IPCC-Bandbreite. Also überschätzt die IPCC-Methode mit den IPCC-Werten den historischen Temperaturanstieg bei Weitem.
Was lehrt uns dieses Missverhältnis zwischen Beobachtung und Berechnung? Da gibt es einige mögliche Erklärungen, die einfach nacheinander aufgezählt werden:
1. Die Sensitivitätswerte sind zu hoch angesetzt, während die Werte für den Antrieb korrekt sind. Falls das der Fall ist, beträgt die Sensitivität +1.5 [+0.5 bis +2.4] Grad pro einer Verdoppelung des CO2. Das ist viel weniger und mit einer kleineren Bandbreite als die +3 [+2 to +4.5] Bandbreite, zu der sich das IPCC versteht.
2. Die Antriebswerte sind zu hoch angesetzt, während die Werte für die Sensitivität korrekt sind. Falls das der Fall ist, erhalten wir eine errechnete Änderung im Antrieb seit 1850 von +0.9 [+0.5 bis +1.4] W/m2. Das ist viel weniger und mit geringerer Bandbreite als die kanonischen IPCC-Werte von +1.7 [+0.7 to +2.5] W/m2, Sonnenantrieb eingeschlossen. Man beachte, dass in diesem und im vorherigen Fall die relativ engen Bandbreiten der Temperaturmessungen noch zusammengepresste Bandbreiten bei den dahinterstehenden Antrieben oder Sensitivitäten haben.
3. Sowohl die Sensitivität als auch die Antriebswerte sind zu hoch angesetzt. Dadurch würde sich die Bandbreite der Möglichkeiten so verringern, dass das Produkt aus beiden Werten +0.7 [+0.5 to +0.9] Grad Erwärmung ergäbe. Falls die Ableitungen proportional wären, müssten Antrieb und Sensitivität um etwa 70% der IPCC-Zahlen reduziert werden.
4. Andere Mechanismen spielen eine Rolle (z. B. kosmische Strahlung, Aerosole aus Plankton, Gewitter), welche das IPCC nicht berücksichtigt.
5. Oder ich habe dumme Rechenfehler gemacht.
6. Möglicherweise gehorcht das Klima aber auch keiner linearen Beziehung zwischen Antrieb und Temperaturveränderung. Meine Berechnungen beruhen auf der IPPC-Annahme, dass die Temperaturveränderung als Konstante namens ("Klimasensitivität" mal Veränderung des Antriebs) berechnet werden kann. Die Klimasensitivität kann aber auch nicht konstant sein (und das ist meine Meinung).
7. Das ist die fehlende Erwärmung, auf die Trenberth hinwies.
8. Etwas ganz anderes, woran ich nicht gedacht habe.
Ich kann überhaupt nicht sagen, was von dem Vorstehenden zutrifft und ob überhaupt etwas davon zutrifft …
Aber immerhin ist das merkwürdig. Falls wir den vom IPCC angegeben historischen Antrieb seit 1850 mit der vom IPCC angegebenen Klimasensitivität multiplizieren, um zu der vom IPCC geschätzten Temperaturänderung zu gelangen, dann entspricht das Ergebnis nicht der historisch gemessenen Temperaturänderung. Die hohe IPCC-Schätzung (2,3 C0) ist dreimal so hoch wie die tatsächliche Änderung (0,7 C0) seit 1850. Da ist doch etwas faul. Je nach gewählter Erklärung kommen wir zu unterschiedlichen Schlussfolgerungen, von denen keine zwingend erscheint.
Nach der Diskussion behandelte Willis Eschenbach das Thema im folgenden Beitrag weiter.
More Oddities with the IPCC Numbers
Einige Leute wiesen mich darauf hin, dass der fehlende Antrieb im Meer gelandet sei, dort befände er sich noch. Daran hatte ich gedacht, aber das hat keinen Sinn ergeben. Ich habe noch einmal alles betrachtet, und es macht immer noch keinen Sinn.
Den IPCC-Rechnungen zufolge fehlen etwa 0,7 W/m2. Nehmen wir mal an, das die latent im Meer vorhanden sind. Hier sind meine Zahlen zur Prüfung. Das Kalkulationsblatt dafür ist hier.
KONSTANTEN
Spezifische Wärme Meerwasser 3.85 Joule/Gramm/C
Meeresvolumen 1.3E+18 m3
Meeresfläche 3.6E+14 m2
Erdoberfläche 5.1E+14 m2
durchschn. Meerestiefe 3700 m
Meeresdichte 1,025 Tonnen/m3
Sekunden pro Jahr 3.2E+07 Sekunden/Jahr
INPUT
"Fehlende" einfallende Strahlung 0.7 W m2 über der Oberfläche
OUTPUT
Equiv. Incoming Radiation To Ocean 1.0 W/m2
Energie/Jahr 3.1E+07 Joule/Jahr
Erwärmungskapazität 8.2E+06 Gramm/C/Jahr
Gewicht einer 1 m2-Säule 3793 Tonnen
Gewicht der Säule 3.8E+09 Gramm
Erwärmung seit 1850 0.11 C (aus dem Kalkulationsblatt)
derzeitige Erwärmungsrate 0.22 C/Jh.
Zeitbedarf zur Erwärmung um 1° bei derzeitiger Rate 465 Jahre/C
Der Grund, warum das für mich keinen Sinn macht, ist folgender: Wenn die Abweichung der vergangenen 150 Jahre das Meer um ein zehntel Grad erwärmt hat, und wenn die latente Wärme (nehmen wir an, dass die 0,7 W/m2 Abweichung erhalten bleibt) weiterhin zu einer Erwärmung von einem Grad über knapp 500 Jahre führt … da kann ich mir einfach nicht vorstellen, dass man das für ein Problem halten kann.
Nehmen wir also an, dass das IPCC recht hat, und dass die Hälfte der einfallenden Energie ins Meer geht und dieses dann mit einer Rate von einem mickrigen halben Grad pro halbes Jahrtausend erwärmt … Und wenn es denn so wäre, hieße das für das praktische Leben, (lassen wir mal das eine Grad im Jahr 2565 außer acht – das ist für die menschliche Vorstellung bedeutungslos) -, dass wir alle IPCC-Erwärmungs-Vorhersagen (Entschuldigung: die Szenarios) um die Hälfte reduzieren müssen? Heißt das nicht, dass die effektive Klimasensitivität in der realen Welt zur Zeit unserer Enkel um das Jahr 2050 nur halb so hoch ist, wie das IPCC verbreitet? Weil nämlich die latente Wärme aus der 0,7 W/m2 Abweichung (0,22 Grad/Jh.) zu einer Meereserwärmung von nicht messbaren 9/100stel Grad im Jahr 2050 führen wird.
Habe ich da etwas übersehen?
Darauf hat Bob Tisdale einen Link für die Zahlen der Meereswärme gegeben. Seine Grafik zeigt einen globalen Meereswärmevorrat, der sich jährlich um 7,8 MJoule pro m2 erhöht.
Wenn meine Zahlen richtig sind (bitte überprüfen), entspricht das einer Wärmeaufnahme (globaler Mittelwert) von 0,7 W/m2. Dies entspricht einer Meereserwärmung von einem Grad in 1900 Jahren. Das, denke ich, können wir vergessen … und es bleibt genug Zeit, damit fertig zu werden.
Die fehlende Erwärmung ist in der Größenordnung von 0,7 W/m2. Nirgendwo finden wir Beweise, dass Wärme in diesem Umfang ins Meer geht. Wenn man die Meereserwärmung als Erklärungsmuster für die fehlende Erwärmung nimmt, fehlt immer ein halbes W/m2 in den IPCC-Schätzungen … Das mathematische Rätsel bleibt. Wer kann das erklären?
Nach meiner Einschätzung ist die Klimasensitivität keine feste Größe, sondern eine Funktion von T, der Temperatur. Sie nimmt mit zunehmender T ab. Das kann man täglich in den Tropen beobachten.
Morgens ist das Meer kühl, und der Himmel klar. Also erwärmt sich die Meeresoberfläche rasch. Die Klimasensitivität (Temperaturänderung in Grad als Ergebnis einer vorgegebenen Veränderung des Antriebs) ist hoch.
So gegen 10:30 Uhr ist die Meeresoberfläche deutlich erwärmt. Als Ergebnis bilden sich nun Kumulus-Wolken. Trotz des zunehmenden Sonnenantriebs erwärmt sich die Meeresoberfläche nicht mehr so rasch. Die Klimasensitivität ist niedriger.
Am Nachmittag bilden sich Gewitter. Die bringen kühle Luft und kühlen Regen von oben und bewegen warme Luft von unten nach oben. Sie kühlen die Meeresoberfläche ab und vermindern die Klimasensitivität auf nahe Null.
Die Gewitter haben eine einzigartige Fähigkeit. Sie können die Oberflächentemperatur unter sich unter die Ausgangstemperatur herunterbringen. In diesem Fall haben wir negative Klimasensitivität – der Antrieb kann weiter zunehmen, die Oberfläche kühlt ab.
Wie man sieht, ist die Wirklichkeit ganz anders aus in Bezug auf die Idee, dass die Temperatur aus einer mythologischen Konstante "Klimasensitivität" mal Antriebsveränderung entstehen würde. In den Tropen nimmt die Klimasensitivität ab, wenn die Temperatur hoch geht. Dort ist die Region, wo das Meiste an Sonnenenergie in unser Klimasystem eintritt.
Willis Eschenbach erchienen am 23.10.10 bei WUWT
Übersetzt von Helmut Jäger EIKE