Gibt Klimalarmist Hansen von der NASA auf? Antwort von Bob Tisdale auf Hansen Artikel: Das Spiel ist aus!

geschrieben von Bob Tisdale | 25. Mai 2012

Datum: 11. Mai 2012
Betreff: New York Times Op-Ed* mit dem Titel “Game Over for the Climate” [etwa: Das Klima hat verloren!”]
[*Besonders in den USA gibt es seit Ende der 30er Jahre des 20. Jahrhunderts die gepflegte Institution des Opposite Editorial (kurz: Op-Ed). Dieses beinhaltet Kommentare von Kolumnisten, die oft bewusst von der Redaktionslinie abweichen. Ursprünglich kommt der Ausdruck daher, dass im Zeitungsdruck diese Meinungsartikel den Herausgeber-Editorials gegenübergestellt waren. Quelle: Wikipedia. A. d. Übers.]
Von: Bob Tisdale
An: James Hansen – NASA GISS
Hallo James:
Ich bin gerade mit der Lektüre deines Meinungsartikels fertig, die in der gestrigen Ausgabe der New York Times erschienen war. Der Titel „Game Over for the Climate“ hat mir so gut gefallen, dass ich mir überlege, den Titel meines Buches in ähnlicher Weise zu ändern, etwa so: „Game Over for the Manmade Global Warming Scare.” [Etwa: „Das Spiel mit der Angst vor der menschengemachten globalen Erwärmung ist aus“]. Ja. Das klingt richtig gut. Danke für die Idee. Ich muss noch herausfinden, wie schwierig es ist, den Titel der Kindle-Edition zu ändern. Während ich mich an dem Titel erfreute, zeigt der Inhalt Ihrer Meinung, dass Sie immer noch die Hoffnung hegen, jene zu erreichen, die naiv genug sind, Ihrer Behauptung Glauben zu schenken, dass CO2 für den jüngsten Schub der globalen Erwärmung verantwortlich ist. Ich hoffe, Sie verstehen, dass viele, viele Menschen von Ihrer Meinung abgefallen sind und sie mangelhaft finden.
Das Internet wurde zum primären Medium bei Diskussionen der anthropogenen globalen Erwärmung, was Sie sicher auch mitbekommen haben. Sie haben Ihren eigenen Blog. Ihr Mitarbeiter am Goddard Institute for Space Studies Gavin Schmidt ist einer der Gründer des einst formidablen Blogs RealClimate. Was Sie möglicherweise nicht mitbekommen haben – einer der anderen Beitragsschreiber bei RealClimate, Rasmus Benestad, hat vor Kurzem in einem Beitrag seinem Gefühl Ausdruck verliehen, dass alle Arbeit dort umsonst gewesen sein könnte:
„Wenn die Auffassung jedoch korrekt ist, dass Informationen wenig Einfluss haben, kann man sich nach dem Sinn fragen, den eine Debatte über Klimaänderung haben soll, und warum bestimmte Organisationen so große Mühen gegen die Leugnung aufwenden, wie es in Büchern wie Heat is on, Climate Cover-up, Republican war on science, Merchants of doubt, und The Hockeystick and Climate Wars beschrieben worden ist. Warum würde es dann solche Dinge wie ‚das Heartland Institute’, ;NIPCC’, climateaudit, WUWT, climatedepot und FoS geben, wenn diese keinen Einfluss hätten? Und auch die Berichte des IPCC und der National Academy of Sciences? Man könnte sich sogar fragen, ob die Mühe, die wir uns bei RealClimate gegeben haben, vergeblich war.“
Ich kann die Zweifel von Rasmus Benestad verstehen, wenn bei einer Website, die der anthropogenen globalen Erwärmung skeptisch gegenübersteht, nämlich WattsUpWithThat, seit 2008 immer mehr Leser vorbeischauen, während RealClimate ins Schwimmen kommt. Das Web-Informationsunternehmen Alexa zeigt, dass die Anzahl der täglichen Zugriffe auf WattsUpWithThat seit Mai 2008 diejenigen bei RealClimate übertroffen hat. Und während der letzten 6 Monate konnte Alexa die Site RealClimate nicht mehr listen, weil der Prozentanteil einfach zu tief gefallen ist. Andererseits haben die täglichen Aufrufe von WattsUpWithThat erheblich zugenommen, und inzwischen ist diese Site zur meistgelesenen Website hinsichtlich globaler Erwärmung und Klimaänderung geworden.
James, während der letzten 30 Jahre oder noch länger haben Sie eine globale Temperaturaufzeichnung erzeugt mit der Bezeichnung GISS Land-Ocean Temperature Index. Er zeigt eine Erwärmung der Oberflächentemperatur seit 1880. Obwohl es einige Probleme mit diesem Datensatz gibt, über die wir reden müssen, ist das etwas, worauf Sie stolz sein können. Aber während dieser 3 Jahrzehnte haben Sie auch Klimamodelle entwickelt und programmiert mit der Festlegung, dass allein anthropogene Treibhausgase für diese Erwärmung verantwortlich waren. Diese Modelle sind mit Dutzenden anderer in den Archiven des IPCC für deren Berichte enthalten. Unglücklicherweise hatten Ihre Bemühungen mit Klimamodellen sowie die Bemühungen anderer Modellierungsgruppen keinen Erfolg. Bei weitem nicht. Und da Ihre Ansichten auf den Ergebnissen Ihrer Klimamodelle basieren, muss man daraus schließen, dass Ihre Ansichten genauso falsch sind wie die Modelle.
Ich bin einer der unabhängigen Forscher, die die auf Messungen basierenden Temperaturaufzeichnungen studieren und dann mit den Ergebnissen der vom IPCC benutzten Klimamodelle vergleichen, die diese Temperaturen simulieren sollen. Andere Forscher und ich selbst verstehen zwei einfache und grundlegende Tatsachen, die unzählige Male auf Blogs wie WattsUpWithThat präsentiert worden sind. Vergessen Sie nicht, dass WattsUpWithThat täglich eine breite Öffentlichkeit erreicht, so dass jeder, der an globaler Erwärmung und Klimaänderung interessiert ist und sich die Zeit nimmt, die Beiträge zu lesen, diese beiden einfachen Tatsachen ebenfalls versteht.
Tatsache eins: Die instrumentenbasierte Aufzeichnung der globalen Temperatur seit 1901 und deren IPCC-Modellsimulationen bestätigen die Hypothese der anthropogenen globalen Erwärmung nicht; sie widersprechen ihr.
Die im 4. Zustandsbericht des IPCC verwendeten Klimamodelle zeigen, dass sich die Temperaturen während der letzten Erwärmungsperiode von 1976 bis 2000 2.9 mal schneller erwärmt haben sollten als während der früheren Erwärmungsperiode von 1917 bis 1944. Die Simulationen der Klimamodelle werden durch Klimaantriebe bestimmt, einschließlich des anthropogenen CO2, die logischerweise während der späteren Erwärmungsphase eine höhere Rate zeigen. Die beobachteten, instrumentenbasierten Erwärmungsraten der beiden Erwärmungsphasen zeigen dagegen etwa die gleiche Rate.
James, falls die Annahme, mit der Sie hausieren gehen, auf festen Füßen stehen würde, hätten das menschliche CO2 und andere anthropogene Treibhausgase die Oberfläche unseres Planeten in den letzten Jahrzehnten viel stärker erwärmen müssen, aber das haben sie nicht. Mit anderen Worten, es gibt kaum Beweise, dass das von Ihnen in Ihrem Op-Ed dämonisierte CO2 überhaupt irgendeine Auswirkung darauf gehabt hätte, wie stark die globale Temperatur gestiegen ist. Wir unabhängigen Klimaforscher haben das schon seit Jahren gewusst. Es taucht immer wieder auf, so oft, dass man in der gesamten Blogosphäre schon Witze darüber reißt.
Einige unabhängige Forscher haben sich Zeit genommen zu zeigen, wie wenig Klimamodelle die Erwärmungs- und Abkühlungsraten seit Beginn des 20. Jahrhunderts simulieren können. Wir tun das, damit Menschen ohne fachliches Hintergrundwissen besser verstehen können, wie sehr das Fundament der Hypothese von der anthropogenen globalen Erwärmung falsch ist. Ich habe das erneut in einem zweiteiligen Beitrag im Dezember 2011 wieder aufleben lassen (hier und hier), die beide auf WattsUpWithThat gepostet worden waren. Ich habe zahlreiche Beiträge darüber seit Dezember mit unterschiedlichen Datensätzen veröffentlicht: Wassertemperatur, Temperatur auf dem Festland und die Kombination beider Datensätze. Ich habe so viele Beiträge veröffentlicht, die zeigen, wie wenig die IPCC-Klimamodelle die Temperaturen der Vergangenheit abbilden, dass ich sie hier nicht alle verlinken kann. In den Beiträgen ging es auch um neue und verbesserte Klimamodelle, die für den bevor stehenden 5. IPCC-Zustandsbericht vorbereitet worden sind. Tut mir leid, aber sie zeigen keine Verbesserung.
Tatsache zwei: Natürliche Prozesse sind für den größten Teil, wenn nicht für die gesamte Erwärmung während der letzten 30 Jahre verantwortlich, einer Erwärmung, die Sie immer noch als Beweis für die Auswirkungen von Treibhausgasen anführen.
In Ihrem Meinungsartikel erwähnten Sie die Vorhersagen, die Sie in Science bereits im Jahre 1981 gemacht hatten. Zufälligerweise haben in jenem Jahr Satellitenmessungen der Wassertemperatur der globalen Ozeane begonnen. Diese Satelliten decken die Messung der globalen Wassertemperatur viel besser ab, von Pol zu Pol. Sie verwenden einen auf Satelliten basierenden Datensatz als einen der Quellen zur Ermittlung der Wassertemperatur für den GISS Land-Ocean Temperature Index (LOTI). Dieser NOAA-Datensatz der Wassertemperatur ist bekannt unter der Bezeichnung Reynolds OI.v2. Es ist der gleiche Datensatz, den ich benutzt habe, um zu illustrieren, dass es natürliche Prozesse und nicht Treibhausgase sind, die für die Erwärmung der globalen Ozeane seit 1981 verantwortlich sind. Da Landmessungen einfach verfügbar sind und Änderungen der Wassertemperatur nachahmen und viel deutlicher sichtbar machen, hat die von Ihnen propagierte Hypothese ein ernstes Problem. Die beobachtungsbasierten Daten widersprechen einmal mehr den Klimamodellen.
Ich bin einer der sehr wenigen Forscher zur globalen Erwärmung, der die Daten der Wassertemperatur und die Prozesse in Verbindung mit der natürlichen Klimaviariabilität studiert, genannt El Niño-Southern Oscillation oder ENSO. ENSO ist ein Prozess, der von vielen Klimawissenschaftlern unterschlagen wird, wenn sie lineare Regressionsanalysen verwenden, um ein ENSO-Signal aus den Aufzeichnungen der globalen Temperatur zu entfernen. Diese Unterschlagungen garantieren irreführende Resultate in einigen klimawissenschaftlichen Studien.
ENSO ist ein natürlicher Prozess, den Sie und Ihre Mitarbeiter beim GISS in vielen, auf Klimamodellen basierenden Studien, die Sie veröffentlichen, außen vor lassen – weil, wie Sie anmerken, Ihr „grob auflösendes Ozeanmodell nicht in der Lage ist, Klimavariationen in Zusammenhang mit ENSO-Prozessen zu simulieren“ (hier). Tatsächlich gibt es beim IPCC kein einziges Modell, das die Häufigkeit, Magnitude und Dauer von El Niño- und La Niña-Ereignissen abbilden kann. Und ich kenne keine wissenschaftliche Studie, die zeigt, dass auch nur ein einziges Klimamodell in der Lage ist, alle fundamentalen gekoppelten Ozean-Atmosphäre-Prozesse in Zusammenhang mit ENSO zu simulieren.
Wenn Klimamodelle nicht in der Lage sind, ENSO zu simulieren, dann enthalten sie nicht einen sehr grundlegenden Prozess von Mutter Natur, dazu gedacht, die Verteilung von Wärme aus den Tropen zu den Polen zu beschleunigen oder verlangsamen. Als Folge davon schließen die Modelle die Variationen aus, mit denen der tropische Pazifik natürlich erzeugte Wärme an die Atmosphäre abgibt und diese innerhalb der Ozeane verteilt, und diese Klimamodelle schließen auch die variierende Rate aus, mit der ENSO für Fernwirkungen bzgl. der Erwärmung in Gebieten sorgt, die weiter entfernt vom tropischen Pazifik liegen.
Klimawissenschaftler müssen damit aufhören, ENSO als Rauschen anzusehen, James! Der ENSO-Prozess fungiert als eine Quelle natürlich erzeugter und gespeicherter thermischer Energie, die abgeleitet, umverteilt und wieder neu angesammelt wird. Weil diese drei Funktionen (Ableitung, Umverteilung und Neuansammlung) alle variieren (siehe Note 1), variieren die Einflüsse von ENSO auf das globale Klima auf jährlicher, vieljähriger und multidekadischer Basis, wenn Frequenz, Magnitude und Dauer von El Niño-Ereignissen diejenigen von La Niña überkompensieren, was zu einer größeren Wärmeabgabe als normal aus dem tropischen Pazifik in die Atmosphäre führt, die dann innerhalb der Ozeane umverteilt wird. Und das Gegenteil geschieht, d. h. die Erde kühlt sich ab, wenn La Niña-Ereignisse über einen multidekadischen Zeitraum El Niño dominieren. Es ist kein Zufall, dass genau dies seit 1917 so abgelaufen ist.
Note 1: El Niño-Ereignissen (dem Abstrahlungsmodus) folgen nicht immer La Niña-Ereignisse (der Ansammlungsmodus). Sowohl El Niño als auch La Niña-Ereignisse können in einer Folge gleichphasiger Ereignisse auftreten, wie es bei den El Niño-Ereignissen 2002/2003, 2004/2005 und 2006/2007 der Fall war. El Niño und La Niña-Ereignisse können auch länger als ein Jahr dauern und mehrere ENSO-Zeiten überdecken, wie z. B. der El Niño von 1986/1987/1988 und das La Niña von 1998/1999/2000. Wenn auf ein starkes El Niño-Ereignis ein La Niña folgt, wie es nach dem Ereignis von 1986/1987/1988 der Fall war, ist sehr offensichtlich, dass zwei Teilphänomene von ENSO zusammen agieren und das warme Wasser umverteilen, das von einem El Niño übrig geblieben ist. Die Folgen dieser kombinierten Auswirkungen sind tatsächlich bei den Aufzeichnungen der Wassertemperatur nur schwer zu übersehen.
Die Temperaturdaten der Satellitenära zeigen, dass ENSO und nicht Kohlendioxid für die Erwärmung der globalen Ozeane in den oberen Schichten während der letzten 30 Jahre verantwortlich ist, wie früher schon angemerkt. Es zeigt, dass die Auswirkungen eines La Niña nicht einfach das Gegenteil von denen eines El Niño sind. Wenn auf starke El Niño-Ereignisse La Niña folgen, deuten die satellitengestützten Daten der Wassertemperatur in der Tat darauf hin, dass beide zusammen agieren und einen Anstieg der Anomalien der Wassertemperatur im Atlantischen sowie dem Indischen und dem westlichen Pazifischen Ozean verursachen können. Und da sich der östliche Pazifische Ozean seit 30 Jahren nicht erwärmt hat, sind diese ENSO-induzierten Anstiege bei den Daten aus dem Atlantik, dem Indik und dem Westpazifik für nahezu die gesamte Erwärmung der Wassertemperatur während der letzten 3 Jahrzehnte verantwortlich.
Ich habe diese ENSO-verursachten Anstiege seit mehr als drei Jahren präsentiert und illustriert. Ich habe die Daten geplottet, habe den ENSO-Prozess diskutiert und animiert, und zwar mit Hilfe zahlreicher Datensätze: Wassertemperatur, Meeresspiegel, Meeresströmungen, ozeanischer Wärmegehalt, tiefengemittelte Temperatur, Warmwasservolumen, Luftdruck auf Meereshöhe, Wolkenmenge, Niederschlag, Stärke und Richtung der Passatwinde usw. Und da die Wolkenmenge im tropischen Pazifik die einfallende kurzwellige Strahlung (sichtbares Licht) beeinflusst, habe ich auch diese Beziehung präsentiert und diskutiert. Die mit diesen Variablen zusammenhängenden Daten bestätigen für meine Leser allesamt, wie die ENSO-Prozesse funktionieren. Sie zeigen und behandeln auch, wie diese Anstiege durch ENSO-Prozesse verursacht werden. Ich habe zu ENSO so viele Beiträge geschrieben, dass ich sie hier nicht alle verlinken kann. Eine sehr gute Übersicht gibt es hier, oder man zieht es vor, die zusätzlichen Kommentare zu lesen auf diesem Beitrag bei WattsUpWithThat.
James, Sie sind sehr herzlich eingeladen, die Suchfunktion auf meiner Website zu nutzen, um die Prozesse von ENSO zu studieren. In aller Bescheidenheit muss ich sagen, dass es dort eine Fülle von Informationen gibt. Ich habe die gleichen Informationen in meinem Buch If the IPCC was Selling Manmade Global Warming as a Product, Would the FTC Stop their deceptive Ads? zusammengestellt. Vielleicht bevorzugen Sie das Buch, dann haben Sie eine kompakte Quelle detaillierter Besprechungen, die in diesem Memo angesprochen werden. Darin wird auch illustriert und diskutiert, wie die vom IPCC im 4. Zustandsbericht verwendeten Klimamodelle den globalen Temperaturverlauf seit 1901 nicht reproduzieren können. Verwendet man diese IPCC-Klimamodelle in einer anderen Gruppe von Vergleichen zeigen sich keine irgendwie gearteten Ähnlichkeiten zwischen der Erwärmung der Wassertemperatur in individuellen Ozeanbecken während der letzten 30 Jahre und wie sich die Wassertemperatur erwärmt haben sollte, falls man das CO2 als alleinige Ursache heranzieht. Eine Übersicht von meinem Buch findet sich im oben verlinkten Beitrag. Bei Amazon gibt es auch eine Kindle-Vorschau, die von der Einführung bis zu einem großen Teil von Abschnitt 2 reicht. Das sind die ersten 15% meines Buches. Beziehen Sie sich auch auf die Einführung, das Inhaltsverzeichnis und den Schluss als .pdf hier. Mein Buch richtet sich an alle mit wenig Hintergrundwissen, so dass jemand wie Sie mit viel Hintergrundwissen bzgl. der Klimawissenschaft leicht in der Lage sein dürfte, das Gesagte zu verstehen.
Abschließend möchte ich noch sagen, dass ich in gewisser Weise überrascht war, Ihren Artikel in der New York Times vom 10. Mai 2012 zu lesen. Ich hatte im zweiten Teil meines Memo vom 21. August 2011 an Sie und Makiko Sato dargelegt, dass ENSO und nicht Kohlendioxid für den jüngsten 30-jährigen Anstieg der globalen Wassertemperatur verantwortlich ist. Dieses Memo können Sie nicht gelesen haben. Hoffentlich lesen Sie dieses hier.
Mit freundlichen Grüßen
Bob Tisdale
Link: http://wattsupwiththat.com/2012/05/12/tisdale-an-unsent-memo-to-james-hansen/
Übersetzt von Chris Frey EIKE



Tisdale nimmt sich Foster & Rahmstorf 2011 vor

geschrieben von Bob Tisdale | 25. Mai 2012

UPDATE 2 (5. Januar 2012): BITTE LESEN! Drei Dinge: Erstens, ich habe den Unterschied zwischen einem „linearen Zeittrend“ (Foster und Rahmstorf, hiernach F&R) und einem „linearen Trend“ nicht verstanden. Meine Konfusion führte auch bei vielen Bloggern zu Konfusion, die meinen Beitrag gelesen und bei WattsUpWithThat kommentiert haben (hier). Dafür möchte ich mich entschuldigen. Für alle Interessierten: der „lineare Zeittrend“ wird unter der Überschrift „Data as trend plus noise” bei Wikipedia beschrieben (hier).
Zweitens habe ich zusätzlich zu MEI, AOD und TSI als unabhängige Variable fälschlich die Werte des linearen Trends verwendet, die EXCEL mit seiner LINEST-Funktion aus den monatlichen GISS-Daten als vierte unabhängige Variable berechnet hat. Und dies addiert sich zu der Konfusion jener, die die Gleichungen interpretiert haben. In der Rückschau denke ich, dass ich diese Gleichungen nicht hätte bringen sollen. Stattdessen hätte ich eine Tabelle bringen sollen, in der die Koeffizienten aufgelistet sind.
Drittens, in der Eile, mit der ich diesen Beitrag veröffentlicht habe, ist es mir nicht gelungen, die Schritte zur Bearbeitung der Daten zu erklären, was Vielen beim Betrachten der Gleichungen und Graphen konfus erscheinen mochte. Ich habe die Regressionsanalysen mit den „rohen“ monatlichen Daten durchgeführt; danach habe ich unter Verwendung der sich ergebenden Koeffizienten die monatlichen Daten angepasst. (Ich hatte einen Graphen unter Verwendung monatlicher Daten vorbereitet, ähnlich der Abbildung 4 bei F&R mit den Jahren 1979 bis 2010 als Basis. Aber ich hatte den Eindruck, dass meine Version ein unintelligenter Spaghetti-Graph mit wenig Aussagekraft war, also habe ich ihn nicht gebracht). Dann habe ich die angepassten Daten in jährliche Daten umgerechnet und schließlich 1979 bis 2010 als Basisjahre herangezogen.
Unter dem Strich: Obwohl ich einen linearen Trend mit einem linearen Zeittrend verwechselt habe, und obwohl ich nicht alle zusätzlichen Feinheiten in den von F&R (2011) verwendeten Daten eingeschlossen habe, ist es schwer, irgendeinen Unterschied zwischen der Abbildung 7 von mir und der Abbildung 5 von F&R zu erkennen. Es gab Kommentare von anderen Bloggern zu dem Beitrag auf WUWT, die mit unterschiedlichen Methoden zu ähnlichen Ergebnissen gekommen waren. Heißt das, dass die Ergebnisse von F&R (2011) so stichhaltig sind wie in einigen Kommentaren bei WUWT behauptet? Nein. ENSO ist ein Prozess, kein Index, und es kann nicht für lineare Regressionsanalysen herhalten. Dies wurde klar gezeigt und detailliert diskutiert unter der Überschrift ENSO IS NOT AN EXOGENOUS FACTOR.
Update 1: (3. Januar 2012): Unter dieser Überschrift habe ich den Wortlaut eines Satzes verändert und das Wort „create“ mit dem Wort „recharge“ ersetzt.

Übersicht

Dieser Beitrag befasst sich mit einem merkwürdigen Aspekt der multiplen linearen Regressionsanalyse von Foster and Rahmstorf der in ihrem 2011 Papier “Global Temperature Evolution 1979–2010” zu finden ist. Ich finde es sehr seltsam, dass der Faktor, auf denen das Papier zu beruhen scheint, nicht im Detail hier vorgestellt wird. Zur Klarstellung für diesen Teil des Beitrages, ich will nicht implizieren, dass  etwas falsch ist mit diesem spezifischen Aspekt des Papiers, aber ich bin auch nicht einverstanden mit ihm. Ich habe es jetzt zur Diskussion hier vorgelegt.
Der zweite Teil dieses Beitrags ist eine Diskussion über eine der exogenen Faktoren, den Foster und Rahmstorf (2011) versucht haben, zu entfernen. Das Problem dabei: Es ist kein exogener Faktor. Und gibt es eine dritte Diskussion über einen Datensatz in einem Tabellenblatt vom Hauptautor Grant Foster (aka Tamino), der aber seltsamerweise nicht im Paper selbst erwähnt wird.
Es ist nicht überraschend, das das Foster und Rahmstorf (2011) Papier  auf den Blogs der Befürworter der anthropogenen globalen Erwärmung die Runde gemacht hat. Joe Romm lobte es mit dem Post "Sorry, ihr Leugner, Die Studie des "True Global Warming Signals" zeigt eine "bemerkenswert stabile" Rate der menschgemachten Erwärmung seit 1979. Und SkepticalScience erläutert das Papier in seinem Beitrag zu Foster und Rahmstorf "Sie messen das Global Warming Signal". Und auch auf RealClimate gab es eine lobende Erwähnung durch die Aufnahme als eines der Themen in ihren Neuigkeiten zur globalen Temperatur.
Einführung
F&R (2011) haben versucht, aus 5 globalen Temperaturdatensätzen die linearen Effekte von drei Faktoren zu entfernen, von denen bekannt ist, dass sie Variationen der globalen Temperatur hervorrufen.
Sie überdeckten die Periode von 1979 bis 2010. Die offensichtliche Absicht der Studie ist es zu zeigen, dass die anthropogene globale Erwärmung unvermindert in allen Datensätzen andauert. Die unabhängigen Variablen, die im Abstract von F&R (2011) aufgelistet werden, sind El Niño-Southern Oscillation, vulkanische Aerosole und solare Variationen. F&R (2011) scheint eine viel klarere Version des Beitrags von Tamino (Grant Foster) vom 20. Januar 2011 zu sein: How Fast is Earth Warming? Nach der Veröffentlichung dieser Studie hat sie Tamino in seinem Beitrag The Real Global Warming Signal diskutiert und freundlicherweise die Quelldaten und den Code in seinem Beitrag Data and Code for Foster & Rahmstorf 2011 zur Verfügung gestellt. Die Daten von Tamino finden sich hier.  Es ist eine .zip-Datei, die Tamino in eine .xls-Datei umbenannt hat, um, wie er erklärt, „die Weltpresse glauben zu machen, dass es sich um eine Excel-Datei handelt. Man muss einen „Rechtsklick und dann Speichern unter…“ durchführen und dabei die Rückbenennung in eine .zip-Datei vornehmen, um sie öffnen zu können.
Wie oben erwähnt haben F&R (2011) die exogenen Faktoren aufgelistet, die als unabhängige Variable in der multiplen Regressionsanalyse als “El Niño/southern oscillation, volcanic aerosols and solar variability“ bezeichnet werden. Komischerweise haben F&R drei Absätze später bei der nochmaligen Auflistung der Faktoren bei der multiplen Regressionsanalyse eine vierte Variable eingeführt: linearer Trend. Der letzte Satz des dritten Absatzes unter der Überschrift „Introduction“ lautet:
„Der Einfluss exogener Faktoren wird durch eine multiple Regression der Temperatur in Abhängigkeit von ENSO, vulkanischer Einflüsse, der gesamtsolaren Einstrahlung und einem linearen Zeittrend durchgeführt, um die globale Erwärmung anzugleichen, die seit 32 Jahren Gegen¬stand der Analyse ist.“
Aber eine der Grundlagen dieser Studie ist es zu illustrieren, wie ähnlich sich die Trends sind, nachdem die Anpassungen für ENSO, Solarstrahlung und vulkanischer Aerosole vorgenommen worden waren, einschließlich der linearen Trends der Datensätze, die in der Regressionsanalyse als eigenartig auffielen. In der Folge machte ich mich daran, nach einem anderen Grund zu suchen, warum F&R diesen linearen Trend in ihre Regressionsanalyse einfließen lassen mussten. Wie ich im Folgenden anmerke, benutze ich kommerzielle Zusatzsoftware für EXCEL, um diese multiple Regressionsanalyse durchzuführen. Da ich keine anderen Mittel habe, die Resultate zu verifizieren, anders als die Ergebnisse eines ihrer Graphen zu reproduzieren, bitte ich Sie, die folgenden Ergebnisse zu bestätigen, wenn Sie diese Möglichkeit haben.
Warum haben sich F&R genötigt gesehen, einen linearen Trend in die multiple Regressionsanalyse einzuführen?
Den einzigen Grund, den ich dafür erkennen kann, ist Folgender: Der Anpassungsfaktor für die solaren Daten ist das falsche Vorzeichen, wenn in der multiplen Regressionsanalyse nur ENSO, solar und vulkanisches Aerosol als unabhängige Variable eingehen. Lassen Sie mich das detaillierter erklären. Aber noch einmal bitte ich zu verstehen, dass ich in diesem Abschnitt des Beitrags nicht impliziere, dass mit diesem spezifischen Aspekt der Studie etwas nicht stimmt; und noch einmal: ich stimme damit nicht überein. Ich fand es nur interessant.
Mit den von Tamino zur Verfügung stellten Daten, habe ich Analyse-It for EXCEL– Software benutzt, um eine multiple Regressionsanalyse durchzuführen. Meine ursprüngliche Analyse schließt ein Taminos Lieblingsdatensatz der Globalen Temperatur nach GISS als abhängige Variable und den mehrdimensionalen ENSO-Index (MEI), die totale Solarstrahlung (PMOD) und die Daten zur Dichte vulkanischen Aerosols (AOD) als unabhängige Variable. Ich habe meine MEI-Daten vier Monate verzögert dargestellt, die PMOD-Daten einen Monat und die AOD-Daten sieben Monate in Übereinstimmung mit Tabelle 1 von F&R (2011), die auch in diesem Beitrag Tabelle 1 ist. Und in dieser Analyse habe ich den GISTEMP linearen Trend als unabhängige Variable nicht berücksichtigt.

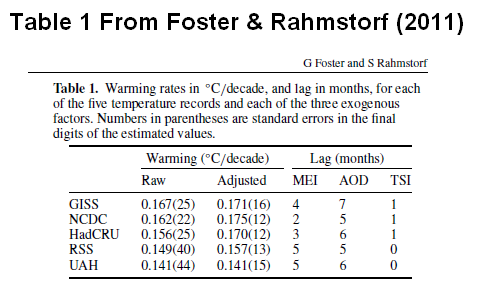
Tabelle 1:
Die multiple Regressionsanalyse allein mit den ENSO (MEI), Solar (PMOD) und vulkanische Aerosole (AOD) ergibt sich aus Gleichung 1:
EQUATION 1:
GISS = 123.6 + 0.06769MEI(4m lag) – 0.09025TSI.PMOD(1m lag)– 3.837AOD (7m lag)
[4m lag etc. = 4 Monate Verzögerung usw. Gilt auch für alle anderen Gleichungen. A. d. Übers.]
Ich habe den Term für die solare Variable [in der Gleichung] in Fettdruck dargestellt, um die Tatsache hervorzuheben, dass das Vorzeichen negativ ist. Er müsste positiv sein, um die Ergebnisse von F&R (2011) zu reproduzieren. Die Vorzeichen von ENSO und für das vulkanische Aerosol entsprechen dem, was man erwartet, siehe Abbildung 1. Gegensätzlich zu F&R ist lediglich das Vorzeichen des Solarkoeffizienten, wie Abbildung 2 zeigt (welche ihre Abbildung 7 ist).

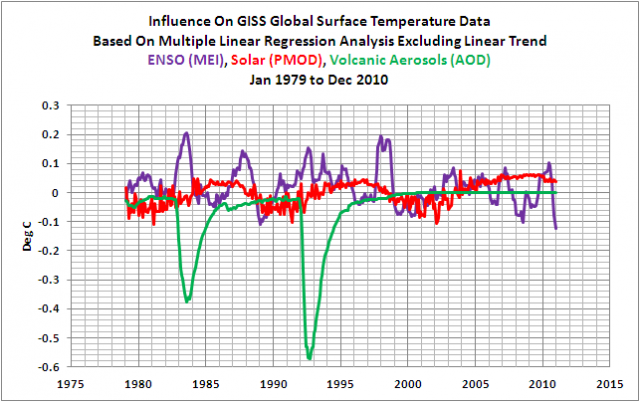
Abbildung 1
HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH

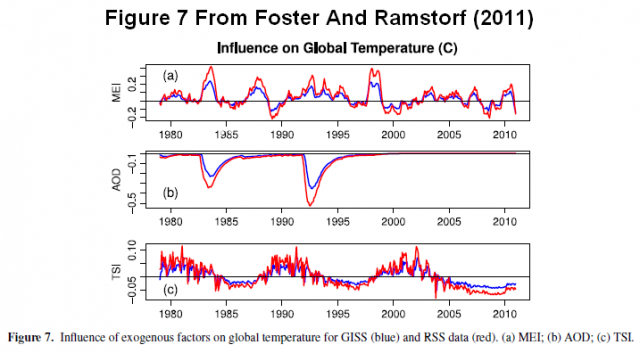
Abbildung 2
Und das ergibt einen monumentalen Unterschied zum Ergebnis von F&R (2011). Wenn wir die GISS-Daten der Temperatur mit den Faktoren aus Gleichung 1 anpassen, ist der Anstieg nicht kontinuierlich. Siehe dazu Abbildung 3. Das Jahr mit der globalen Temperaturspitze der adjustierten GISS-Daten ist das Jahr 2002.

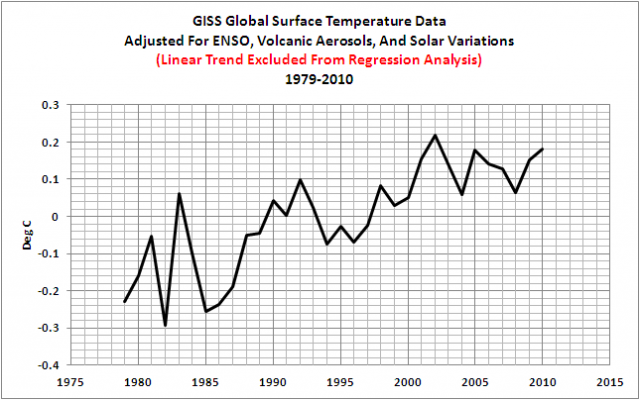
Abbildung 3
Um die Ergebnisse von F&R (2011) zu stützen, habe ich einen linearen Trend von 0,167°C pro Dekade zu den Anomaliedaten von GISS als unabhängige Variable hinzugefügt. Die Verzögerungen von ENSO (MEI), Solar (PMOD) und vulkanisches Aerosol (AOD) bleiben die gleichen wie zuvor.
Die multiple Regressionsanalyse mit ENSO (MEI), Solar (PMOD) und vulkanisches Aerosol (AOD) und dem linearen Trend ergibt sich aus Gleichung 2:
EQUATION 2:
GISS = -91.43 + 1.024Trend + 0.0761MEI(4m lag) + 0.06694TSI.PMOD(1m lag)– 2.334AOD (7m lag)
Das Vorzeichen des Koeffizienten der Sonneneinstrahlung stimmt jetzt mit F&R überein, wie Abbildung 4 zeigt. Man beachte, dass die Einführung des linearen Trends als unabhängige Variable auch die Skalierung der anderen drei Variablen verändert. Es hat den Skalierungsfaktor der ENSO-Daten etwas zunehmen lassen und den Skalierungsfaktor des vulkanischen Aerosols signifikant abnehmen lassen. Natürlich ergibt die Einführung des Trends als unabhängige Variable mit der Änderung des Vorzeichens der Solarstrahlung auch mit den GISS-Daten das von F&R gewünschte Ergebnis, Abbildung 5, mit einem relativ stetigen Temperaturanstieg während des 32-jährigen Zeitraumes. Und man beachte, dass der Trend von 0,172°C pro Dekade mit den Ergebnissen von F&R (2011) vergleichbar ist, die in Tabelle 1 gelistet sind.

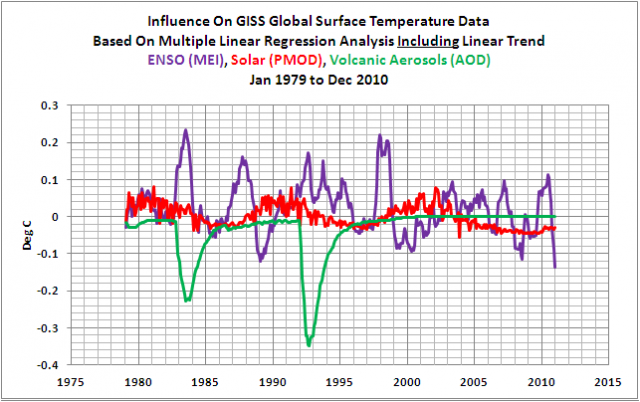
Abbildung 4
HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH

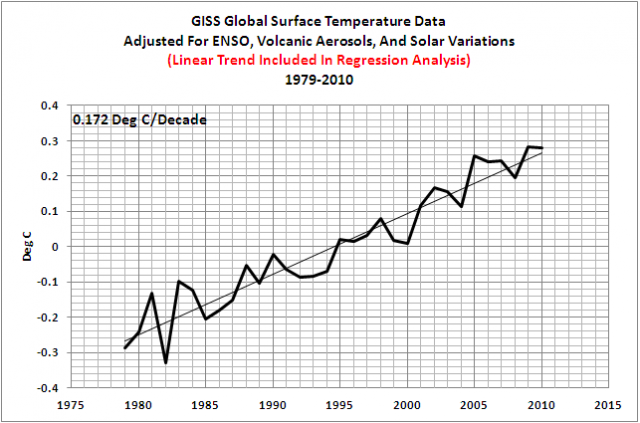
Abbildung 5
Natürlich habe ich die Trendanpassung aus Gleichung 2 nicht eingeführt (und F&R (2011) konnten sie nicht einführen), als ich die korrigierten Daten in Abbildung 5 gezeigt habe. Nachdem die Trendanpassung mit eingeschlossen war, würden die korrigierten Daten keinen Trend aufweisen. Das bedeutet: wie es scheint, mussten F&R (2011) den Trend in den GISSTEMP-Daten in die Regressionsanalyse einführen, nur um das Vorzeichen des solaren Einflusses zu bekommen, das sie haben wollten.
F&R (2011) hätten ähnliche Faktoren der Skalierung für die ENSO (MEI)-, PMOD- und AOD-Daten erhalten, wenn sie die GISS-Temperaturdaten nur trendbereinigt hätten.
EQUATION 3:
Detrended GISS = -86.31 + 0.0759MEI(4m lag) + 0.0632TSI.PMOD(1m lag) – 2.37AOD (7m lag)
Das umgekehrte Vorzeichen des solaren Einflusses haben alle globalen Datensätze der Temperatur gemeinsam.
Nun könnte man geneigt sein zu fragen, ob der GISS-Datensatz der globalen Temperatur der einzige Datensatz mit diesen Ergebnissen ist. Die Antwort lautet nein. Wenn der lineare Trend nicht in die linearen multiplen Regressionsanalysen eingeführt wird, steht das Vorzeichen des Solarkoeffizienten immer im Gegensatz zu dem, was F&R (2011) hätten benutzen müssen für die NCDC und HADCRUT Land- plus Wassertemperaturdaten sowie für die Temperaturdaten der unteren Troposphäre von RSS und UAH. Die Gleichungen 4 bis 7 liegen den Regressionsanalysen dieser Datensätze zugrunde. Die Verzögerungen sind die gleichen wie in Tabelle 1 oben gelistet:
EQUATION 4 (NCDC Land Plus Meeresoberflächentemperatur):
NCDC = 109.1 + 0.05495MEI(2m lag) – 0.0796TSI.PMOD(1m lag)– 3.113AOD (5m lag)
EQUATION 5 (Hadley Centre HADCRUT Global Surface Temperature Anomalies):
HadCRUT3v = 92.21 + 0.06421MEI(3m lag) – 0.0673TSI.PMOD(1m lag)– 3.293AOD (6m lag)
EQUATION 6 (RSS MSU Lower Troposphere Temperature Anomalies):
RSS33 = 61.44 + 0.1285MEI(5m lag) – 0.04489TSI.PMOD(0m lag)– 4.863AOD (5m lag)
EQUATION 7 (UAH MSU Lower Troposphere Temperature Anomalies):
UAH = 72.94 + 0.1332MEI(5m lag) – 0.05338TSI.PMOD(0m lag)– 5.139AOD (6m lag)
Wenn wir diese Koeffizienten verwenden, ergibt sich aus den fünf Datensätzen keineswegs der nette kontinuierliche Anstieg der globalen Temperatur, den F&R so gerne präsentiert hätten, wie Abbildung 6 zeigt. Für die drei Datensätze (GISS, HADCRUT, NCDC) war das Jahr 2002 das wärmste. Lediglich die beiden Datensätze der Temperaturanomalien in der unteren Troposphäre zeigen 2010 als das wärmste Jahr.

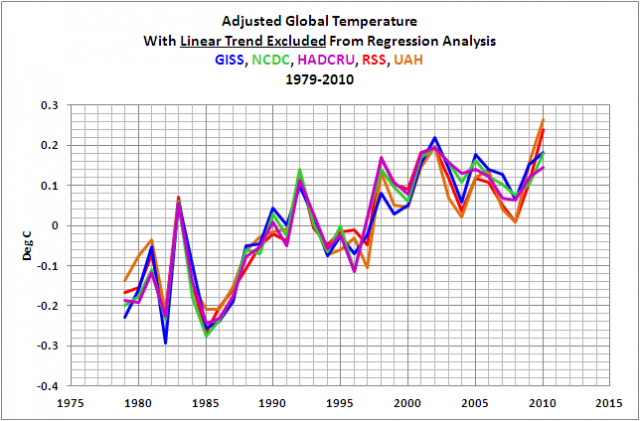
Abbildung 6
Und wie zu erwarten war, wenn die linearen Trends der anderen globalen Temperaturdatensätze als unabhängige Variable mit einbezogen werden, wird das Vorzeichen des Solarkoeffizienten positiv. Siehe die Gleichungen 8 bis 11.
EQUATION 8 (NCDC Land Plus Ocean Surface Temperature, with trend):
NCDC = -106.7 + 1.085Trend + 0.06832MEI(2m lag) + 0.07813TSI.PMOD(1m lag)– 1.68AOD (5m lag)
EQUATION 9 (Hadley Centre HADCRUT Global Surface Temperature Anomalies, with trend):
HadCRUT3v = -119.2 + 1.093Trend + 0.07519MEI(3m lag) + 0.08723TSI.PMOD(1m lag)– 1.858AOD (6m lag)
EQUATION 10 (RSS MSU Lower Troposphere Temperature Anomalies, with trend):
RSS33 = -135.5 + 1.05Trend + 0.1342MEI(5m lag) + 0.09923TSI.PMOD(0m lag)– 3.479AOD (5m lag)
EQUATION 11 (UAH MSU Lower Troposphere Temperature Anomalies, with trend):
UAH = -105.7 + 0.9953Trend + 0.1381MEI(5m lag) + 0.07742TSI.PMOD(0m lag)– 3.871AOD (6m lag)
Schließt man die linearen Trends in die multiplen Regressionsanalysen mit ein, ergeben die Koeffizienten aus den obigen Gleichungen die Anpassungen, die F&R (2011) präsentiert haben, Abbildung 7. Ich habe ihre Abbildung 5 als Abbildung 8 als Referenz hier mitgezeigt.

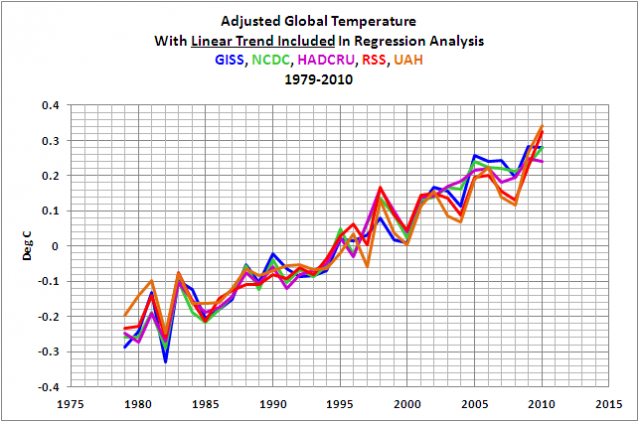
Abbildung 7
HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH

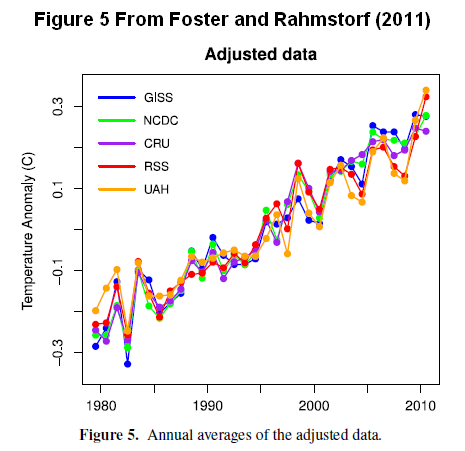
Abbildung 8

Die Annahme über den linearen Trend

Ich bin sicher, dass irgendeiner versuchen wird zu argumentieren, dass die Mitberücksichtigung des Trends in den Regressionsanalysen notwendig ist, da die auf Computermodellen basierenden Studien gezeigt haben, dass der Anstieg der globalen Temperatur in der Periode 1979 bis 2010 durch anthropogene Antriebe verursacht worden ist. Aber natürlich setzt diese Argumentation voraus, dass man die Klimamodelle verwenden kann, den Grund für einen Anstieg der globalen Temperatur während jeder beliebigen Periode zu bestimmen. Wir haben vor Kurzem gezeigt und diskutiert, dass die vom IPCC in ihrem 4. Zustandsbericht verwendeten  Klimamodelle die globalen Temperaturen in keiner Periode des 20. Jahrhunderts darstellen konnten. Siehe hierzu den zusammenfassenden Beitrag  hier. Das zweite Problem mit ihrer Annahme besteht darin, dass die globalen Ozeane, die etwa 70% der Erdoberfläche überdecken, während der Satellitenära keine Anzeichen einer anthropogenen globalen Erwärmung zeigen. Und das bringt uns zu…

ENSO ist kein exogener Faktor

F&R (2011) haben versucht, ENSO als einen exogenen Faktor von den Instrumentenaufzeichnungen abzuziehen. Aber ENSO ist kein exogener Faktor. ENSO ist ein gekoppelter Ozean-Atmosphäre-Prozess, der periodisch während eines El Niño Wärme in die Atmosphäre bringt. Der El Niño verursacht Änderungen in der atmosphärischen Zirkulation, was zu variierenden Temperaturen außerhalb des östlichen tropischen Pazifiks führt, teils Erwärmung, teils Abkühlung, aber insgesamt überkompensieren die warmen Gebiete die kühlen, und die globale Temperatur steigt als Reaktion auf einen El Niño. Die Verteilung von Erwärmung und Abkühlung während eines La Niña sind denen eines El Niño ähnlich, aber die Vorzeichen sind umgekehrt. Und das ist wirklich alles, worauf Studien wie die von F&R (2011) die Hoffnung begründen können, dass sich die Berücksichtigung von ENSO in den Regressionsanalysen auszahlt. Aber ENSO bedeutet noch viel mehr.
ENSO ist auch ein Prozess, der das vom El Niño selbst übrig gelassene Warmwasser umverteilt und die Verteilung des El-Niño-Warmwassers außerhalb des östlichen tropischen Pazifik verstärkt. Bei dieser Umverteilung wird warmes Wasser polwärts transportiert sowie in die angrenzenden Ozeanbecken während eines einem El Niño folgenden La Niña. La Niña-Ereignisse erwärmen auch einen Teil des Warmwassers verursacht durch El Niño. Manchmal „überladen“ La Niña-Ereignisse den tropischen Pazifik insofern, als sie mehr tropische Ozeanwärme des Pazifiks erzeugen als vorher durch El Niño entstanden war. Das war so während der La Niña-Ereignisse 1973/74/75/76 und 1995/96. Siehe Abbildung 9. Das La Niña-Ereignis von 1973/74/75/76 stellte den Initial-“Treibstoff” für den Super El Niño von 1982/83 und den mehrjährigen El Niño von 1986/87/88. Und der „El Niño des Jahrhunderts” 1997/98 wurde durch La Niña von 1995/96 angeregt. Der Prozess ENSO kann durch lineare Regression nicht in einem Index berücksichtigt werden. Dies wurde in der Einführung zu dem Beitrag ENSO Indices Do Not Represent The Process Of ENSO Or Its Impact On Global Temperature illustriert und diskutiert.

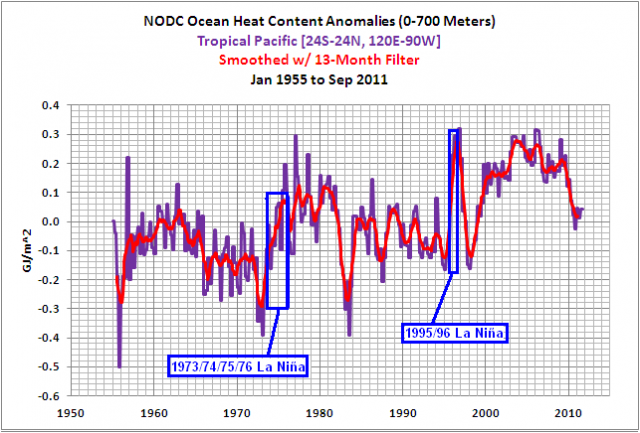
Abbildung 9
F&R (2011) bezogen sich auf Trenberth et al. (2002) Evolution of El Nino–Southern Oscillation and global atmospheric surface temperatures” als eine ihrer Referenzen zu ENSO. Aber Trenberth et al. (2002) erwähnen das folgende Dementi im zweiten Absatz ihrer Schlussfolgerungen (ihr Absatz 52, Fettdruck von mir):
Das in dieser Studie benutzte wesentliche Tool ist die Korrelation und Regressionsanalyse, die durch kleinste Quadrate-Anpassungen [?] dazu tendiert, größere Ereignisse zu betonen. Dies erscheint angebracht, weil in diesen Ereignissen das Signal ganz klar größer ist als das Rauschen. Mehr noch, diese Methode wichtet jedes Ereignis angemessen (anders als in vielen Komposit-Analysen). Obwohl es möglich ist, die Regression dazu zu verwenden, den linearen Anteil des globalen Temperatursignals in Zusammenhang mit ENSO zu eliminieren, weichen die regional zum globalen Mittel beitragenden Prozesse erheblich voneinander ab, und die lineare Annäherung verlässt wahrscheinlich ein ENSO Überbleibsel.
Die ENSO-„Reste” liefern einen signifikanten Beitrag zum Anstieg der globalen Wassertemperaturwährend der Satellitenära, wie wir noch sehen werden. Haben F&R (2011) diese Reste in ihren Analysen berücksichtigt? Nein. Sie haben angenommen, dass der Anstieg durch anthropogene Antriebe erfolgt ist, und sie vermuteten, dass ein linearer Trend dies repräsentiert.
Eine jüngere Studie ist von F&R (2011) übersehen worden. Compo und Sardesmukhs (2010) Beitrag “Removing ENSO-Related Variations from the Climate Record” scheint ein Schritt in die richtige Richtung zu sein. Sie schreiben (Fettdruck von mir):
Eine wichtige Frage bei der Abschätzung des Klimas im 20. Jahrhundert lautet, in welchem Ausmaß durch ENSO verursachte Variationen zum beobachteten Trend beigetragen haben. Diese Beiträge zu isolieren ist aus vielerlei Gründen eine Herausforderung, einschließlich Mehrdeutigkeiten, wie ENSO definiert wird. Im Besonderen kann die Definition von ENSO mit einem einzigen Index und die mit diesem ENSO in Zusammenhang stehenden Variationen als Regression über diesen Index, wie es in vielen früheren Studien getan worden ist, zu falschen Schlussfolgerungen führen. Diese Studie sagt, dass man ENSO am besten untersuchen kann, wenn man es nicht als Zahl, sondern als einen sich entwickelnden dynamischen Prozess für dieses Ziel betrachtet.
Und wie Compo und Sardeshmukh vermutet haben, kamen F&R (2011) zu den falschen Schlussfolgerungen.
Beachte: Compo und Sardeshmukh lagen bei einem sehr wichtigen Aspekt von ENSO daneben. Sie haben die Signifikanz der riesigen Menge warmen Wassers übersehen, die von den El Niño-Ereignissen übrig gelassen worden sind, und sie haben nicht den Beitrag dieses Vorgangs zum Anstieg der globalen Wassertemperatur-Anomalie seit etwa 1976 gesehen.
Wir wollen auch nicht die vielgepriesene Studie von Thompson et al. (2008) vergessen. Diese Studie von Thompson et al. (2008) für den neuen und verbesserten HADSST3-Datensatz der globalen Wassertemperatur-Anomalie vom Hadley Centre. Bei Thompson et al. (2008) wurde wie bei F&R (2011) gemogelt, weil sie versuchen, das ENSO-Signal aus den Aufzeichnungen globalen Temperaturaufzeichnung zu entfernen und dann behaupten, dass der restliche Temperaturanstieg durch anthropogene Antriebe verursacht wird. In ihrer Einführung schreiben Thompson et al. (2008) (Fettdruck von mir):
In dieser Studie werten wir eine Reihe neuer Methoden aus, um aus den ungeglätteten Datenreihen der globalen Land- und Wassertemperaturen die Varianz in Verbindung mit ENSO zu identifizieren und herauszufiltern, ebenso die dynamisch induzierte atmosphärische Variabilität und Vulkanausbrüche. Die Auswirkungen von ENSO und von Vulkanausbrüchen auf die globale mittlere Temperatur werden mit Hilfe eines einfachen thermodynamischen Modells der Reaktion der Durchmischungsschicht Atmosphäre – Ozean auf eine anomale Erwärmung geschätzt. Im Falle eines ENSO wird vermutet, dass die Erwärmung proportional zu den Anomalien der Wassertemperatur im östlichen Pazifik ist…“
Das ist eine monumentale Hypothese, und es ist die gleiche bewusst irreführende Hypothese von F&R (2011).
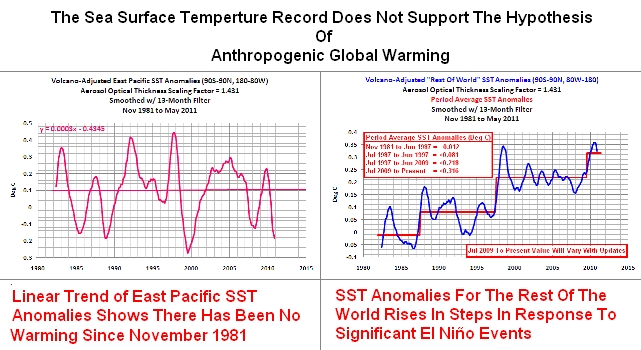
Aber es war diese spezielle Sprache bei Thompson et al. (2008), die mich dazu veranlasst hat, die Anomalien der Wassertemperatur in die zwei Unter-Datensätze aufzuteilen. Einer zeigt die Anomalie im Ostpazifik von Pol zu Pol (90S – 90N, 180 – 80W) und der andere den Rest der Welt (Atlantik – Indischer Ozean – Westpazifik) von Pol zu Pol (90S – 90N, 80 W-180). Und rein zufällig habe ich den Datensatz der Wassertemperatur benutzt (Reynolds OI.v2), der auch für den Land-Ozean-Index von GISS benutzt wird, welcher Taminos bevorzugter Datensatz der Temperaturanomalien ist. Ich habe die Wassertemperaturen der beiden Datensätze zum ersten Mal am 3. März 2011 präsentiert, und zwar hier. (Für Interessierte gibt es ungefähr ein Dutzend zusätzliche Beiträge, in denen ENSO und die vieljährigen Folgewirkungen spezifischer ENSO-Ereignisse behandelt werden. Sie sind am Ende dieses Beitrags verlinkt.)
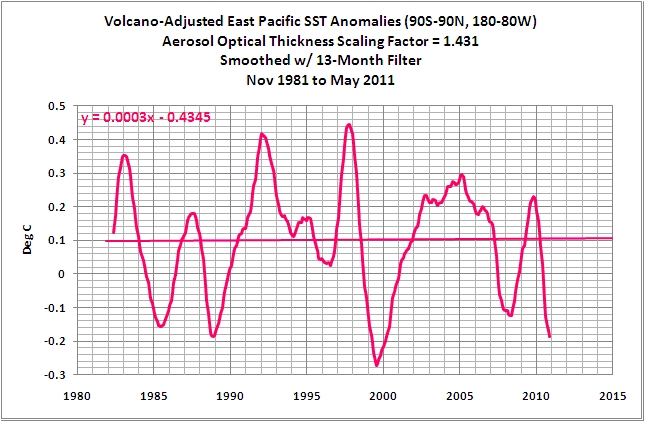
Die Anomalien der Wassertemperatur im Ostpazifik von Pol zu Pol, Abbildung 10, werden beherrscht von den Variationen im tropischen Pazifik, hervorgerufen durch ENSO, und als Folge imitieren die Variationen der Wassertemperatur im Ostpazifik ENSO, repräsentiert durch die skalierten NINO3.4-Anomalien der Wassertemperatur. Der Trend der Wassertemperatur im Ostpazifik ist relativ flach und beträgt 0,011°C pro Dekade.

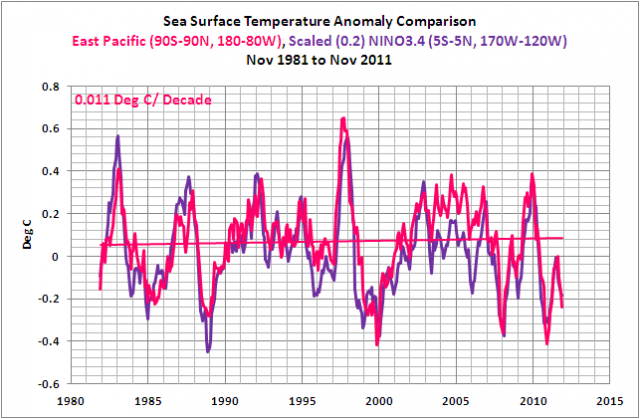
Abbildung 10
Der Grund für diesen flachen Trend: Warmes Wasser an und unter der Oberfläche im Wärmepool des westlichen Pazifiks wird während eines El Niño ostwärts transportiert und breitet sich an der Oberfläche des östlichen tropischen Pazifiks aus, was dort zu einem Anstieg der Wassertemperatur führt. Und während der den El Niño folgenden La Niñas wird das übrig gebliebene Warmwasser in den westlichen tropischen Pazifik zurück transportiert. Wegen der gesteigerten Stärke des Passatwinde während eines La Niña kommt es zu einem verstärkten Aufquellen kälteren Tiefenwassers im östlichen äquatorialen Pazifik, so dass die Wassertemperatur dort sinkt. Mit anderen Worten, der Ostpazifik ist nichts weiter als ein Sammelpunkt für das warme Wasser eines El Niño-Ereignisses. Warmes Wasser schwappt in diesem Datensatz aus dem westlichen tropischen Pazifik und setzt Wärme frei, bevor das warme Wasser wieder zurück schwappt.
Aber das warme Wasser unter der Oberfläche des Wärmepools im Westpazifik während eines El Niño beeinflussen nicht nur die Wassertemperatur in allen globalen Ozeanen, und man kann sie nicht mit einem ENSO-Index darstellen. Das übrige Warmwasser wird während eines auf einen El Niño folgenden La Niña in den Westpazifik zurück geführt, wobei viel davon an der Oberfläche verbleibt. Die Wassertemperatur im westlichen Pazifik steigt daher. Auf einer Breite von etwa 10N transportiert auch eine sich langsam verlagernde Rossby-Welle übriggebliebenes Warmwasser vom östlichen tropischen Pazifik zurück zum westlichen Pazifik während eines La Niña. Meeresströmungen transportieren das warme Wasser polwärts in das erweiterte Strömungssystem Kuroshio – Oyashiro (KOE) östlich von Japan und zur südpazifischen Konvergenzzone (SPCZ) östlich von Australien, und der Indonesische Durchfluss [Indonesian Throughflow] (eine Meeresströmung) transportiert warmes Wasser in den tropischen Indischen Ozean. Und wie oben erwähnt quillt verstärkt kaltes Tiefenwasser während eines La Niña aufgrund der stärkeren Passatwinde im östlichen tropischen Pazifik auf, so dass die Wassertemperatur dort zurückgeht. Aber dieses Wasser, kälter als normal, wird während La Niña rasch erwärmt, da es durch die verstärkten Passatwinde westwärts strömt. Und der Grund, warum sich das Wasser bei dieser Westverlagerung so rasch erwärmt, ist Folgender: die verstärkten Passatwinde reduzieren die Wolkenbildung, so dass die kurzwellige Sonnenstrahlung (das sichtbare Sonnenlicht) das Wasser bis zu einer gewissen Tiefe erwärmt. Dieses zusätzliche Warmwasser hilft, die Wassertemperaturen im Westpazifik und dem Ostindischen Ozean während La Niña auf einem höheren Niveau zu halten, und es füttert auch den westpazifischen Wärmepool bis zum nächsten El Niño. Siehe nochmals Abbildung 9, aber man beachte dabei, dass diese Abbildung den ozeanischen Wärmegehalt für den gesamten tropischen Pazifik darstellt und nicht nur für den pazifischen Wärmepool.
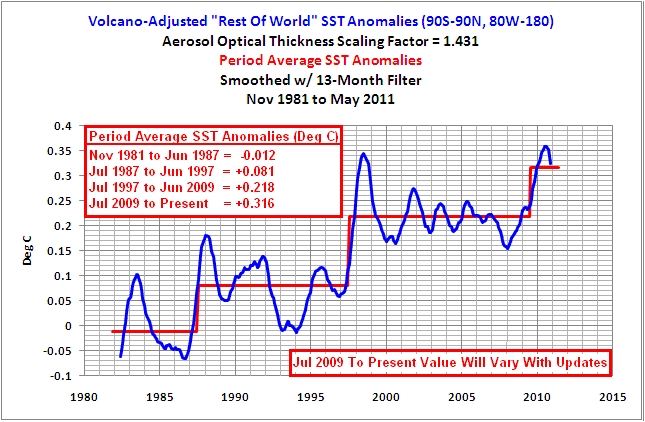
Und was passiert, wenn ein starkes El Niño-Ereignis von einem La Niña gefolgt wird? Die Anomalien der Wassertemperatur für den Atlantik, den Indischen und den Westpazifischen Ozean (alle Ozeane außerhalb des Ostpazifik) nehmen als erstes zu, und zwar als Reaktion auf den El Niño; die El Niño-Ereignisse von 1986/87/88 und 1997/98. Danach werden die Wassertemperaturen dieser Ozeane durch La Niña auf einem erhöhten Niveau gehalten; die La Niña-Ereignisse 1988/89 und 1998/99/00/01. Die Folgen sind die offensichtlich steigenden Anomalien der Wassertemperatur in diesen Ozeanen von Pol zu Pol (90S-90N, 80W-180), wie in Abbildung 11 gezeigt.

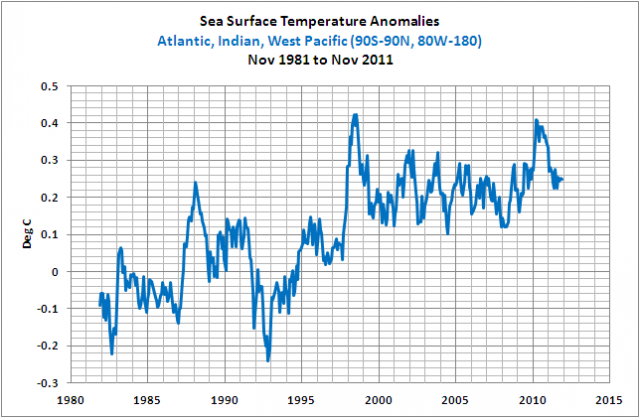
Abbildung 11
Der Abfall und die Erholung mit Beginn im Jahre 1991 wurden verursacht durch die vulkanischen Aerosole der Explosion des Mount Pinatubo. Und der Grund dafür, warum die Wassertemperatur-Anomalien in den anderen Ozeanen so gering auf den Super-El Niño von 1982/83 reagieren, liegt darin, dass der Ausbruch des El Chichon im Jahre 1982 der Erwärmung entgegen wirkte.
Um den Lesern zu versichern, dass der Anstieg der Wassertemperaturen in den Ozeanen außerhalb des Pazifik mit den El Niño-Ereignissen von 1986/87/88 und 1997/98 zusammenfällt, habe ich einen ENSO-Index, NINO3.4 Wassertemperatur-Anomalien in Abbildung 12 eingezeichnet. Die NINO3.4 Wassertemperatur-Anomalien wurden (multipliziert mit dem Faktor 0,12) skaliert, um einen besseren augenscheinlichen Vergleich zu ermöglichen. Außerdem habe ich ihn um 6 Monate verschoben, um der Zeitverzögerung zwischen den Variationen in NINO3.4 und der Reaktion der Daten der übrigen Ozeane Rechnung zu tragen.

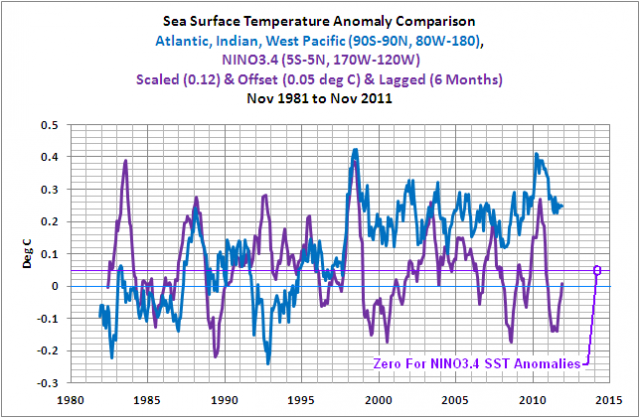
Abbildung 12
Aber der ENSO-Index rauscht sichtlich und lenkt von der Zunahme ab. Darum habe ich in Abbildung 13 die Daten zwischen den signifikanten El Niño-Ereignissen isoliert. Für diesen Zweck habe ich den  Oceanic Nino Index (ONI) der NOAA verwendet, um die offiziellen Monate dieser El Niño-Ereignisse zu bestimmen. Es gibt eine 6-monatige Zeitverschiebung zwischen den NINO3.4-Anomalien und der Reaktion der Wassertemperatur-Anomalien in den restlichen Ozeanen während der Entwicklungsphase des El Niño von 1997/98. Also wurden die ONI-Daten um sechs Monate verschoben, und die Daten der Wassertemperatur der übrigen Ozeane, die auf die El Niño-Ereignisse von 1982/83, 1986/87/88 und 2009/10 reagiert haben, wurden ausgeschlossen – übrig gelassen als schwarze gestrichelte Linien. Alle anderen Monate mit Daten verbleiben.

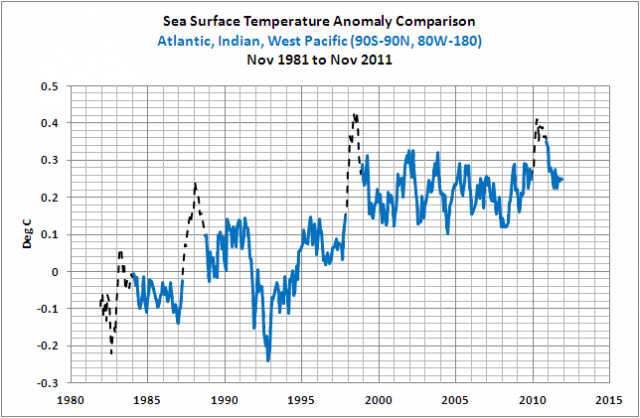
Abbildung 13
Und um den Anstieg weiter zu beleuchten, wurden in Abbildung 14 die mittleren Anomalien der Wassertemperatur zwischen großen El Niño-Ereignissen hinzugefügt.

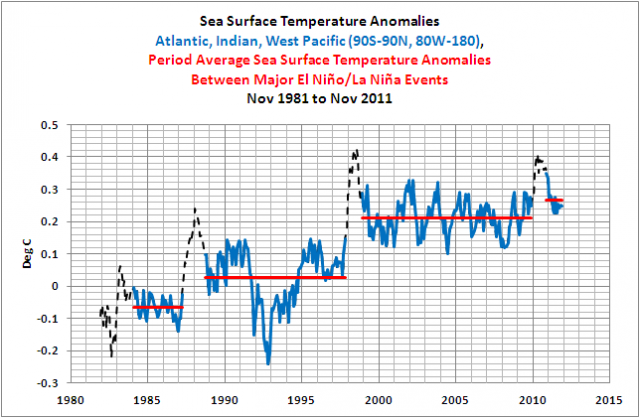
Abbildung 14
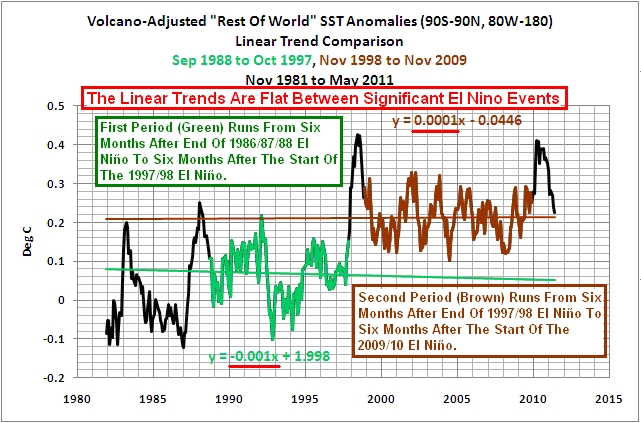
Basierend auf früheren Beiträgen, in denen ich den gleichen Datensatz präsentiert habe, schlugen einige Kommentatoren vor, dass die Zeitspannen der Mitteltemperaturen irreführend sind, und verlangen, dass ich die linearen Trends illustriere. Abbildung 15 zeigt, wie flach die Trends zwischen den El Niño-Ereignissen von 1986/87/88 und 1997/98 sowie zwischen denen von 1997/98 und 2009/10 waren.

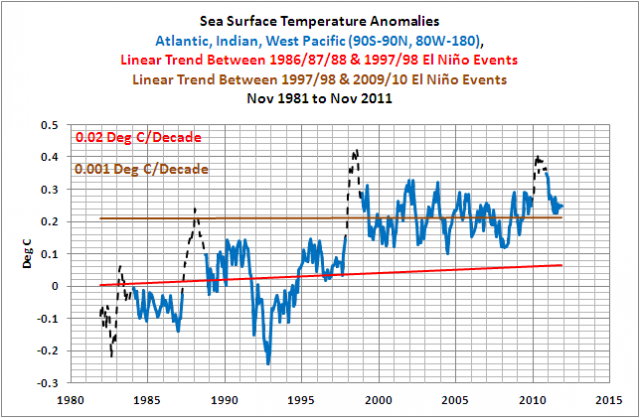
Abbildung 15
Zurück zu den Daten aus dem Ostpazifik: Falls man die Anomalien der Wassertemperatur im Ostpazifik anpasst, um den Effekte vulkanischer Aerosole Rechnung zu tragen, ist der lineare Trend leicht negativ (Abbildung 16). Mit anderen Worten, für etwa 33% der Fläche der globalen Ozeane sind die Anomalien der Wassertemperatur seit 30 Jahren nicht gestiegen.

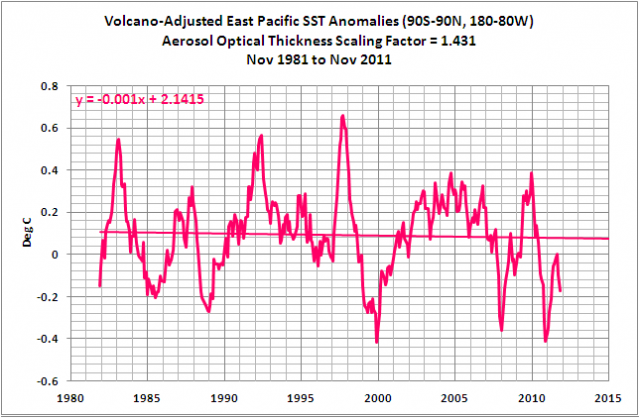
Abbildung 16
Bemerkung: Die Methode zur Anpassung bzgl. von Vulkanausbrüchen wird hier beschrieben, und zwar im Absatz unter der Überschrift ACCOUNTING FOR THE IMPACTS OF VOLCANIC ERUPTIONS.
Und wenn wir die Anomalien der Wassertemperatur in den übrigen Ozeanen bzgl. vulkanischer Eruptionen anpassen (Abbildung 17), reduzieren wir die Effekte des Abfalls und der Erholung durch die Eruption des Mount Pinatubo 1991. Und der Trend in diesen Ozeanen zwischen den El Niño-Ereignissen von 1986/87/88 und 1997/98 ist leicht fallend verglichen mit den nicht angepassten Daten (Abbildung 15), was den Trend noch flacher und leicht negativ macht.

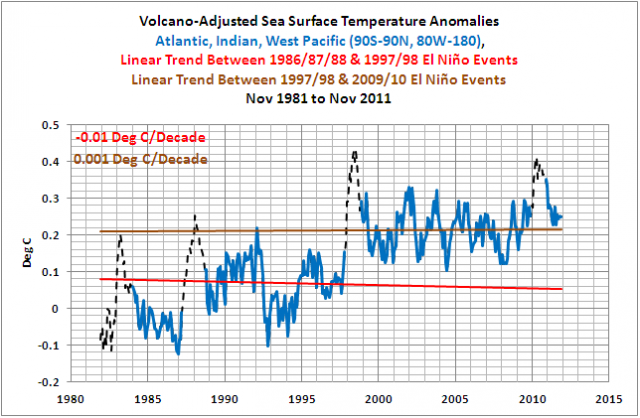
Abbildung 17
Zusammenfassend: ENSO ist ein gekoppelter Ozean-Atmosphäre-Prozess, und seine Auswirkungen auf die globalen Temperaturen können nicht mit einem ENSO-Index dargestellt werden, wie es F&R (2011) versucht haben – und andere vor ihnen. Wir können einfach die Studie von F&R (2011) zu der Liste zahlreicher Studien hinzufügen, die den gleichen Fehler machen. Beispiele:
Lean and Rind (2009) How Will Earth’s Surface Temperature Change in Future Decades?
Und:
Lean and Rind (2008) How Natural and Anthropogenic Influences Alter Global and Regional Surface Temperatures: 1889 to 2006
Und:
Santer et al (2001), Accounting for the effects of volcanoes and ENSO in comparisons of modeled and observed temperature trends
Und:
Thompson et al (2008), Identifying signatures of natural climate variability in time series of global-mean surface temperature: Methodology and Insights
Und:
Trenberth et al (2002) Evolution of El Nino–Southern Oscillation and global atmospheric surface temperatures
Und:
Wigley, T. M. L. (2000), ENSO, volcanoes, and record-breaking temperatures
Außerdem haben F&R (2011) vermutet, dass das Signal der globalen Erwärmung linear ist und dass es durch anthropogene Antriebe verursacht wird, aber diese Vermutungen werden durch die Messungen der Wassertemperatur in der Satellitenära nicht gestützt, wie oben gezeigt wurde. Das Signal der globalen Erwärmung ist nicht linear, und es wurde gezeigt, dass die El Niño-Ereignisse von 1986/87/88 und 1997/98 der Grund für den Anstieg der Wassertemperatur war und nicht anthropogene Treibhausgase.

Die atlantische multidekadische Oszillation

Wenn man Taminos Datei allfit2.xls heruntergeladen hat (hier – und es danach zu einem .zip.file gemacht hat), wird man bemerken, dass die erste Spalte AA als „AMO“ bezeichnet ist. Und ja, das sind die Daten der multidekadischen Oszillation von der AMO website des NOAA Earth System Research Laboratory (ESRL).
Man beachte: Die jüngsten AMO-Daten und die in Taminos Datei aufgelisteten Daten sind etwas unterschiedlich. Der Grund: Die ESRL AMO-Daten entwickeln sich ständig. Jeden Monat nachdem die neuen Daten der Wassertemperatur im Nordatlantik (0 – 70N, 80W – 0) hinzugefügt worden sind, werden die Daten mit den neuen Daten trendbereinigt.
Man kann nur darüber spekulieren, warum Tamino die AMO-Daten mit aufgeführt hat – und warum die Daten auf dem Arbeitsblatt bis zum Jahr 1950 zurückreichen, wenn es in der Studie lediglich um den Zeitraum 1979 bis 2010 geht. Und man kann sich auch fragen, warum Tamino die ESRL AMO-Daten mitführt, welche auf den Kaplan-Anomaliedaten der Wassertemperatur im Nordatlantik basieren, wenn diese Kaplan-Daten in keinem anderen Datensatz genutzt werden (GISS, HADCRUT oder NCDC). Die Datensätze sind nicht die gleichen. Ich habe Tamino und seine Jünger schon auf diesen Fehler hingewiesen, und zwar in dem Beitrag Comments On Tamino’s AMO Post.
Aber die Neugier beispielsweise kann befriedigt werden. Nehmen wir an, man fragt sich, wie die Ergebnisse aussehen würden, wenn man auf den Einfluss der AMO auf die Temperaturen der Nordhemisphäre zählt, unter Verwendung einer linearen Regressionsanalyse mit den ESRL AMO-Daten als unabhängige Variable und den GISS-Daten der nordhemisphärischen Temperatur als die abhängige Variable. Wir begrenzen das Beispiel auf die von F&R (2011) betrachtete Zeitspanne von 1979 bis 2010. Siehe Abbildung 18. Die AMO-angepasste nordhemisphärische Temperatur besitzt einen linearen Trend, der lediglich 41% der nicht angepassten Daten der Nordhemisphäre ausmacht.
Hmm. Das würde bedeuten, dass die AMO für 59% des Temperaturanstiegs in der Nordhemisphäre verantwortlich war, wenn man die Regressionsanalyse zugrunde legt.

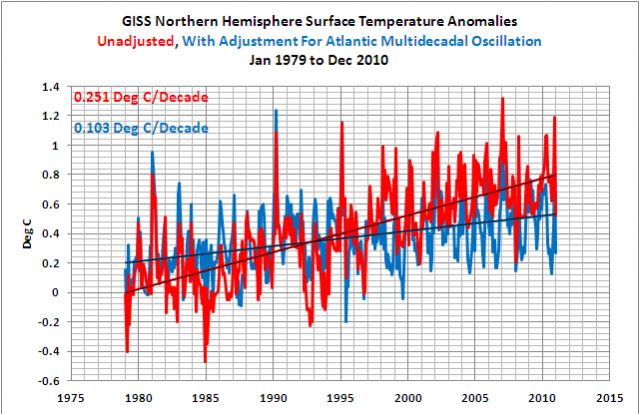
Abbildung 18
Und das liegt auf einer Linie mit der Generalisierung durch Taminos Erfüllungsgehilfen auf RealClimate und dort auf ihrer Atlantic Multidecadal Oscillation (“AMO”) – Website. Dort schreiben sie zur AMO:
Eine multidekadische Verteilung (50 bis 80 Jahre) der nordatlantischen Ozean-Atmosphäre-Variabilität, dessen Existenz durch Verweis auf die statistischen Analysen von beobachteten und Proxy-Daten begründet wird, und den Simulationen des gekoppelten Atmosphere-Ocean General Circulation Model (“AOGCM”). Von dieser Verteilung glaubt man, dass man mit ihr die beobachtete Erwärmung im frühen 20. Jahrhundert (zwanziger und dreißiger Jahre) erklären kann und auch einen Anteil, aber nicht der gesamten, der Erwärmung in hohen Breiten im ausgehenden 20. Jahrhundert. Der Term wurde in einer Zusammenfassung von Kerr (2000)  eingeführt, und zwar aufgrund einer Studie von Delworth und Mann (2000).
Tamino fährt fort, sich darüber zu beklagen, dass man keine Anpassungen wegen der AMO vornehmen kann, weil sie eine Komponente der globalen Erwärmung enthält. Zum Beispiel schreibt Tamino in einer Antwort auf einen Kommentar von Colin Aldridge am 22. Dezember 2011 (hier):
Wenn es um die AMO geht, IST es Temperatur, anders als ENSO (oder PDO in dieser Sache). Klar und einfach, nicht mehr und nicht weniger. Eine Temperaturänderung einer Temperaturänderung zuzuordnen scheint irgendwie dumm zu sein.
Hmm. Ich glaube, dass Tamino nicht den Punkt getroffen hat, dass nämlich die AMO eine zusätzliche Variabilität einbringt und dass sie über den gesamten Datenterm trendbereinigt wird.
Um hier weiterzukommen, habe ich Tamino erklärt und illustriert, dass wir das „Erwärmungssignal“ in der globalen Wassertemperatur mit Ausnahme des Nordatlantik von den Anomalien der Wassertemperatur im Nordatlantik abziehen können. Dann bleibt nur die zusätzliche Variabilität der Wassertemperaturen im Nordatlantik verursacht durch die AMO übrig. Und nur so sollte die AMO dargestellt werden. Den Unterschied nennen wir die Nordatlantische Restgröße. Diese Restgröße hat in etwa den gleichen Trend wie die AMO im F&R (2011)-Zeitraum von 1979 bis 2010, wie Abbildung 19 zeigt:

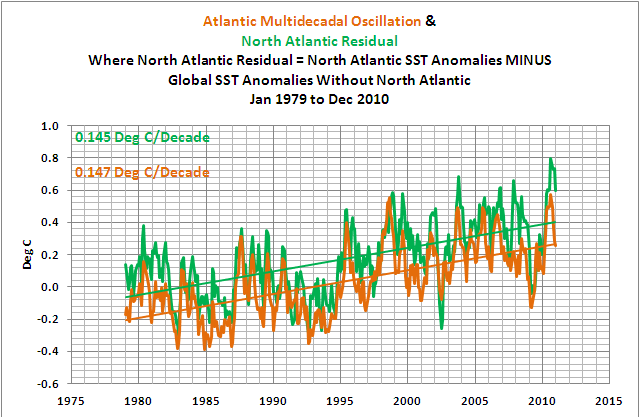
Abbildung 19
Zur Beachtung: Die Daten der nordatlantischen Restgröße in Abbildung 16 basieren auf einer Kombination der HADISST-Daten von 1979 bis November 1981 und den ReynoldsOI.v2-Daten von Dezember 1981 bis zur Gegenwart, und zwar in Übereinstimmung mit GISS, dargestellt auf der Website der GISS Surface Temperature Analysis. Um die Wassertemperatur des Nordatlantik aus den globalen Daten der Wassertemperatur zu entfernen wurde festgelegt, dass die Fläche des Nordatlantik zwischen 0 – 70N und 80W – 0 11% der Fläche der globalen Ozeane ausmacht.
Und als einen zusätzlichen Check des Vorzeichens der solaren Korrektur habe ich multiple lineare Regressionsanalysen der nordhemisphärischen Temperaturen von GISS als der abhängigen Variable und die AMO-Daten als eine unabhängige Variable in einem Augenblick in die nordatlantische Restgröße in einer Sekunde durchgeführt. Die Analysen umfassten auch ENSO (MEI), Solar (PMOD) und vulkanische Aerosole (AOD.NH) als unabhängige Variable mit der gleichen Zeitverzögerung wie in den globalen Daten. In beiden Fällen stand das Vorzeichen der solaren Korrektur im Gegensatz zu dem, was F&R (2011) gesucht haben, wie die Gleichungen 12 und 13 zeigen:
EQUATION 12:
GISS.NH = 62.25 + 0.001696MEI (4m lag) – 0.04528TSI.PMOD(1m lag)– 1.683AOD.NH (7m lag) + 0.866AMO (0m lag)
EQUATION 13:
GISS.NH = 72.12 + 0.04751MEI (4m lag) – 0.05258TSI.PMOD(1m lag)– 2.413AOD.NH (7m lag) + 0.72N. Atl. Residual (0m lag)
Abschließende Bemerkung zur AMO: Für eine erweiterte Diskussion darüber, wie der Nordatlantik die Wassertemperaturen in der Zeitspanne zwischen den Aufwärtssprüngen der El Niño-Ereignisse von 1986/87/88 und 1997/98 schaue man hier: Supplement To “ENSO Indices Do Not Represent The Process Of ENSO Or Its Impact On Global Temperature”

Schlussbemerkungen

Ich fand das Hinzuziehen eines linearen Trends in den von F&R (2011) durchgeführten Regressionsanalysen sehr interessant. Es scheint, als seien diese linearen Trends einfach deshalb hinzugefügt worden, um das Vorzeichen der solaren Korrektur zu dem zu machen, was die Autoren für ihre Anpassungen gerne sehen wollten. Man könnte denken, wenn die grundlegenden Ergebnisse der Studie davon abhängig wären, ob ein linearer Trend in die multiplen Regressionsanalysen eingeführt wird, wäre es in der Studie behandelt worden. Und noch einmal, wenn Sie die Fähigkeit haben und mit den Ähnlichkeiten zwischen meinen Ergebnissen und denen von F&R (2011) nicht zufrieden sein sollten (Abbildungen 7 und 8), bestätigen Sie bitte die Ergebnisse der oben präsentierten Ergebnisse der multiplen Regressionsanalysen mit und ohne den linearen Trend.
Dieser Beitrag hat auch den Fehler in ihren Hypothesen deutlich gemacht und diskutiert, dass nämlich die Regressionsanalyse verwendet werden kann, um die Auswirkungen von ENSO auf die globale Temperatur zu entfernen. ENSO ist ein Prozess, der nicht vollständig durch ENSO-Indizes beschrieben werden kann. Mit anderen Worten, die ENSO-Indizes repräsentieren nur einen kleinen Teil der Auswirkungen von ENSO auf die globale Temperatur. Der Versuch, den ENSO-Index so zu verwenden, wie es F&R (2011) getan haben, gleicht dem Versuch, ein Baseballspiel allein von der Ausgangsposition des Spielfeldes aus zu spielen.
Es wurde gezeigt, dass die Hypothese von F&R (2011), dass ein linearer Trend ein ungefähres Signal „globaler Erwärmung“ bereitstellt, hinsichtlich der Wassertemperatur irrig ist. Spaltet man die Daten in zwei logische Unterdatensätze auf, nämlich Ostpazifik einerseits und die übrigen Ozeane andererseits, zeigen die satellitengestützten Werte der Wassertemperatur keinen Beweis für ein Signal einer anthropogenen globalen Erwärmung. Sie zeigen lediglich Sprünge nach oben im Zuge starker ENSO-Ereignisse. Dies scheint jeden Versuch zu komplizieren, die Hinzunahme eines linearen Trends zur Umkehrung des Vorzeichens der solaren Anpassung zu rechtfertigen.
Und Dank an Tamino, dass der die Daten der multidekadischen atlantischen Oszillation auf seinem Arbeitsblatt vermerkt hat. Dies erlaubte es mir, die signifikante Auswirkung zu zeigen, die die AMO auf die Temperaturen der Nordhemisphäre haben kann.
ABOUT: Bob Tisdale – Climate Observations
QUELLEN (aus Zeitgründen nicht mitübersetzt)
The spreadsheet that served as the source of the data for the regression analyses was linked to Tamino’s (Grant Foster’s) post Data and Code for Foster & Rahmstorf 2011.
To save you some time, here’s a copy of the file that contains the spreadsheet from Tamino’s blog that I’ve uploaded to mine, allfit2 as of 12-21-11.  Again, you’ll have to download the file and change it to a .zip file in order to open it.
The Reynolds OI.v2 Sea Surface Temperature data used in the ENSO discussion is available through the NOAA NOMADS website here.
The Aerosol Optical Thickness data used in the volcano adjustments of the Sea Surface Temperature data in Figures 13 and 14 is available from GISS the Stratospheric Aerosol Optical Thickness webpage here.
Link: http://wattsupwiththat.com/2012/01/02/tisdale-takes-on-taminos-foster-rahmstorf-2011/
Übersetzt von Chris Frey für EIKE

Nachtrag 21.1.12:

Wie u.a. ein Leser auf Science Sceptical richtig schrieb, hat Autor Bob Tisdale  am 2. Januar einen fachliche Kritik zum Foster/Rahmstorf-Artikel veröffentlicht. Oben lesen Sie die übersetzte Version davon. Das Original ist hier: Tisdale takes on Tamino’s Foster & Rahmstorf 2011. Sie enthält jedoch einige Fehler.
Bob Tisdale hatte dann am 14.Januar den Folgeartikel Tisdale takes on Foster & Rahmstorf – take 2 veröffentlicht, in dessen Vorspann er die Mängel seines 1.Artikels ausführlich erläutert hatte. In diesem zweiten Artikel selbst konzentrierte er sich ganz auf ENSO und zog die Konsequenzen aus den Ungenauigkeiten seines ersten Artikels. Da unsere Übersetzungskapazitäten derzeit bis zum Anschlag ausgefüllt sind verweisen wir für die Details auf das englische Original.
Die Redaktion



Korrelation zwischen SST und AGW – Stützen die Aufzeichnungen der Wassertemperatur (SST) die Hypothese von der anthropogenen globalen Erwärmung?

geschrieben von Bob Tisdale | 25. Mai 2012

Dieser Beitrag steht inhaltlich auch mit dem Beitrag How Can Things So Obvious Be Overlooked By The Climate Science Community? in Zusammenhang. Hier stelle ich jedoch einen besseren Weg vor, und zwar mit der Unterteilung in dekadenübergreifende Perioden, die einmal vom Ende des El Niño der Jahre 1986/87/88 bis zum Beginn des El Niño 1997/98 sowie vom Ende des El Niño 1997/98 bis zum Beginn des El Niño von 2009/2010. Dies ermöglicht einen viel konsistenteren Weg, um die aktuellen SST-Anomalien der übrigen Welt zwischen diesen bedeutenden El Niño-Ereignissen zu ermitteln.

DIE ANTWORT AUF DIE TITELFRAGE BESTEHT NUR AUS EINEM EINZIGEN WORT: NEIN!

Die seit Beginn des Satellitenzeitalters ermittelten Temperaturaufzeichnungen deuten darauf hin, dass die SST nur als Reaktion auf bedeutende El Niño-Ereignisse gestiegen waren. Mit anderen Worten, die SST-Daten widersprechen der IPCC-Hypothese, dass der größte Teil des Anstiegs von den anthropogenen Treibhausgasen verursacht worden ist.

Die Tatsache, dass die per Satellit gemessenen SST-Anomalien AGW nicht stützen, kann man sehr leicht mit den beiden Graphen in Abbildung 1 illustrieren. Sie zeigen die per Satellit gemessenen SST-Anomalien in zwei Bereichen der globalen Ozeane, und zwar unter Verwendung der Reynolds OI.v2 SST-Daten von November 1981 (Beginn der Datenreihe) bis zum Mai 2011. Der Graph links zeigt die vulkanbereinigten SST für den Ostpazifik von Pol zu Pol (90°N bis 90°S; 180° bis 80°W). Das Gebiet repräsentiert etwa 33% der globalen Ozeanfläche. Es gibt wesentliche Variationen von Jahr zu Jahr, verursacht durch El Niño und La Niña-Ereignisse, aber ihr linearer Trend ist nahezu flach bei einer Steigung von +0,003°C pro Dekade. Mit anderen Worten, es hat während fast 30 Jahren keinen Anstieg der vulkanbereinigten SST-Daten für diesen Teil der globalen Ozeane gegeben. Der Graph rechts zeigt die vulkanbereinigten SST-Anomalien für alle übrigen Gebiete der Welt. Die SST-Anomalien in diesem Teil des Globus zeigen zwei deutliche Anstiege mit Perioden von fast keinem Anstieg dazwischen. Die Anstiege werden durch die mittleren SST-Anomalien für den Zeitraum zwischen den durch El Niño-Southern Oscillation-Ereignissen verursachten Anstiegen verdeutlicht. Es gibt einen Anstieg im Jahre 1987 als Reaktion des El Niño von 1986/87/88, sowie einen weiteren im Jahre 1997 als Reaktion auf den El Niño von 1997/98. Man erkennt auch, wie die SST-Daten in der übrigen Welt als Reaktion auf El Niño von 2009/2010 erneut steigen.

Abbildung 1

Die Abbildungen 2 und 3 zeigen die beiden Graphen in voller Größe. Diese Datensätze habe ich zum ersten Mal in meinem Beitrag Sea Surface Temperature Anomalies – East Pacific Versus The Rest Of The World besprochen, und sie erschienen seitdem in meinen monatlichen Aktualisierungen der SST-Anomalien. Zwei Anmerkungen: Der SST-Datensatz in diesem Beitrag stammt aus der NOAA Optimum Interpolation, Version 2 SST, auch bekannt als Reynolds OI.v2. Und wie in der Diskussion zu Abbildung 1 schon angemerkt, wurden beide Datensätze von den Effekten der Vulkanexplosionen von El Chichon 1982 und Mount Pinatubo 1991 bereinigt. Ich führte eine lineare Regressionsanalyse der globalen SST-Anomalien durch, um den Einflüssen der vulkanischen Aerosole Rechnung zu tragen. Näheres hierzu in dem o. g. Beitrag.

Abbildung 2

############################################

Abbildung 3

Der Trend der SST in der übrigen Welt zwischen den signifikanten El Niño-Ereignissen

Oben habe ich gezeigt, dass die SST-Daten der übrigen Welt zwei deutliche Anstiege zeigen und fast keine Änderung im Zeitraum dazwischen. Tatsächlich beträgt der Trend zwischen den El Niño-Ereignissen von 1986/87/88 und 1997/98 -0,01°C pro Dekade und der zwischen dem letztgenannten und dem El Niño von 2009/2010 +0,001°C pro Dekade. Mit anderen Worten, diese SST-Daten waren als Reaktion auf die signifikanten El Niño-Ereignisse der achtziger und neunziger Jahre angestiegen und zeigten keinen Anstieg im über eine Dekade langen Zeitraum dazwischen.

Abbildung 4

Um die Zeiträume zwischen den El Niño-Ereignissen abzugrenzen, habe ich den Oceanic Nino Index (ONI) von NOAA genutzt, um offiziell die Monate der drei El Niño-Ereignisse festlegen zu können.  Es gibt eine zeitliche Lücke von 6 Monaten zwischen den NINO3.4 SST-Anomalien und der Reaktion der SST in der übrigen Welt während der Entwicklungsphase des El Niño von 1997/98. Also verlegte ich die ONI-Daten ebenfalls um sechs Monate und alle SST-Daten aus der übrigen Welt, die mit den drei genannten El Niño-Ereignissen korrespondieren. Dann führte ich die Trendanalyse für die beiden verbleibenden Zeiträume durch.

Es wird sicher welche geben, die versuchen, die Trendanalysen der Abbildung 4 herunter zu spielen, und zwar mit der Bemerkung, dass ich die Daten nach Juni 2009 ausgeschlossen habe, um einen Anstieg der SST-Daten zu verschleiern. In Wirklichkeit habe ich diese Daten aber nur ausgeschlossen, weil durch das El Niño-Ereignis von 2009/2010 offenbar ein weiterer Anstieg erfolgte, wie in Abbildung 3 ersichtlich.

Schlussbemerkungen

Wenn nicht allein die anthropogenen Treibhausgase die SST-Anomalien während der El Niño-Ereignisse von 1986/87/88 und 1997/98 beeinflusst haben, gibt es in den per Satellit gemessenen SST-Daten keinen Beweis einer anthropogenen globalen Erwärmung. Die vulkanbereinigten SST-Anomalien im Ostpazifik sind während der letzten 30 Jahre nicht größer geworden. In der übrigen Welt sind die vulkanbereinigten SST-Anomalien nur während der beiden erwähnten El Niño-Ereignisse größer geworden, während sie in den Zwischenzeiten keine Änderung gezeigt hatten.

Ich habe die ENSO-Ereignisse sowie die vieljährigen Folgewirkungen von ENSO während der letzten Jahre in vielen Beiträgen beschrieben und präsentiert. Links dazu sind unter der Überschrift „Weitere Informationen“ unten aufgelistet.

ENSO ist ein Prozess, bei dem periodisch Wärme aus den Ozeanen abgeleitet und warmes Wasser aus dem tropischen Pazifik neu verteilt wird. ENSO sorgt auch dafür, dass die Wärme aus dem tropischen Pazifik durch eine periodische Zunahme von kurzwelliger Strahlung stromabwärts regeneriert wird. In dieser Hinsicht nehmen ENSO-Ereignisse ihre Energie aus einer periodischen Zunahme des natürlichen Strahlungsantriebs (solare Energie) über dem tropischen Pazifik. Wenn El Niño-Ereignisse sich über einen multidekadischen Zeitraum erstrecken, was darauf hindeutet, dass der tropische Pazifik mehr ozeanische Wärme als „normal“ freisetzt und weit verteilt, steigen die globalen Temperaturen. Das Gegenteil ist der Fall, wenn La Niña-Ereignisse dominieren.

Quellen

Daten der SST-Anomalien sind auf der NOAA NOMADS-Website verfügbar:
http://nomad1.ncep.noaa.gov/cgi-bin/pdisp_sst.sh
oder:
http://nomad3.ncep.noaa.gov/cgi-bin/pdisp_sst.sh?lite

Daten zur optischen Dicke des globalen stratosphärischen Aerosols von GISS findet man hier:

http://data.giss.nasa.gov/modelforce/strataer/tau_line.txt

Früherer Beitrag von Tisdale, auf den er sich in der Einführung bezieht:

Sea Surface Temperature Anomalies – East Pacific Versus The Rest Of The Worl d

Weitere Information

Meine ersten detaillierten Beiträge der vieljährigen Nachwirkungen von ENSO sind:
Can El Nino Events Explain All of the Global Warming Since 1976? – Part 1
und:
Can El Nino Events Explain All of the Global Warming Since 1976? – Part 2
und:
Supplement To “Can El Nino Events Explain All Of The Warming Since 1976?”
und:
Supplement 2 To “Can El Nino Events Explain All Of The Warming Since 1976?”

Und für jene, die visuelle Hilfsmittel bevorzugen, gibt es hier zwei Videos:                 

La Niña Is Not The Opposite Of El Niño – The Videos.

Die Auswirkungen dieser El Niño-Ereignisse auf den Nordatlantik werden hier behandelt:
There Are Also El Nino-Induced Step Changes In The North Atlantic
und:
Atlantic Meridional Overturning Circulation Data

Ich habe auch eine Erwiderung auf den Beitrag Tamino’s AMO Post geschrieben. Ich hoffe, demnächst einen neuen beitrag zum Nordatlantik fertigt zu haben.

Die Beiträge über die Auswirkungen von ENSO und Wärmegehalt der Ozeane sind hier:
ENSO Dominates NODC Ocean Heat Content (0-700 Meters) Data
und:
North Atlantic Ocean Heat Content (0-700 Meters) Is Governed By Natural Variables

Zusätzliche detaillierte technische Diskussionen findet man hier:
More Detail On The Multiyear Aftereffects Of ENSO – Part 1 – El Nino Events Warm The Oceans
und:
More Detail On The Multiyear Aftereffects Of ENSO – Part 2 – La Nina Events Recharge The Heat Released By El Nino Events AND…During Major Traditional ENSO Events, Warm Water Is Redistributed Via Ocean Currents.
und:
More Detail On The Multiyear Aftereffects Of ENSO – Part 3 – East Indian & West Pacific Oceans Can Warm In Response To Both El Nino & La Nina Events

Alle Beiträge des Autors Bob Tisdale

Link: http://wattsupwiththat.com/2011/07/10/tisdale-on-sst-correlation-with-agw/

Übersetzt von Chris Frey für EIKE

 



GISS streicht Temperaturdaten aus der Arktis und Daten der Wassertemperatur in den südlichen Ozeanen um die Antarktis

geschrieben von Bob Tisdale | 25. Mai 2012

Die hier schon öfter dargestellten Gründe dafür sind: das GISS benutzt einen Radius von 1200 km um einen Messpunkt, um über Gebiete mit spärlichem Meldungsumfang interpolieren zu können, und das Gebiet mit dem größten Einfluss darauf ist die Arktis.  Typischerweise schließt das eine Karte oder einen Vergleich mit anderen Karten der globalen Temperaturabweichung ein, ähnlich wie in Abb. 1. Die oberen zwei Karten wurden aus Abb. 3 in einem Beitrag auf Real Climate mit dem Titel „2009 temperatures by Jim Hansen” entnommen. Die dritte Karte habe ich hinzugefügt.

Die untere Karte stammt von der GISS Website Global Maps . Sie zeigt die globale Anomalie der Temperatur mit einem Gitterpunktsabstand von 250 km des Jahres 2005, dem gleichen Jahr wie die Darstellung in den oberen beiden Karten mit dem 1200–km–Radius. 

Man richte sein Augenmerk auf die Arktis und auf die südlichen Ozeane rings um die Antarktis. Bemerken Sie einen Unterschied?


Abb. 1 Die oberen beiden Karten sind dem Beitrag “Temperaturen 2009 von Jim Hansen“ auf RealClimate entnommen.

Die untere Karte stammt von der GISS Global Maps Webpage.

Es wird keine Temperaturskala eingefügt, weil die Karten lediglich den Vergleich der flächenmäßigen Abdeckung beim HadCRUT und GISTEMP mit einem Gitterpunktsabstand von 250 km zeigen sollen. Als Referenz dient die obere Karte von GISTEMP mit einem Abstand von 1200 km.

GISS eliminiert Werte der Wassertemperatur im Polarmeer

Die Hauptregionen, in denen GISS die Temperaturwerte eliminiert, zeigt Abb. 2. Drei Gebiete sind hervorgehoben: Zwei über dem Arktischen Ozean (= Polarmeer) und das dritte rund um die Antarktis. Dies wird im Folgenden genauer erklärt. GISS verwendet dann seinen 1200-km-Radius und ersetzt die Daten über dem Ozean durch Daten von Landstationen.

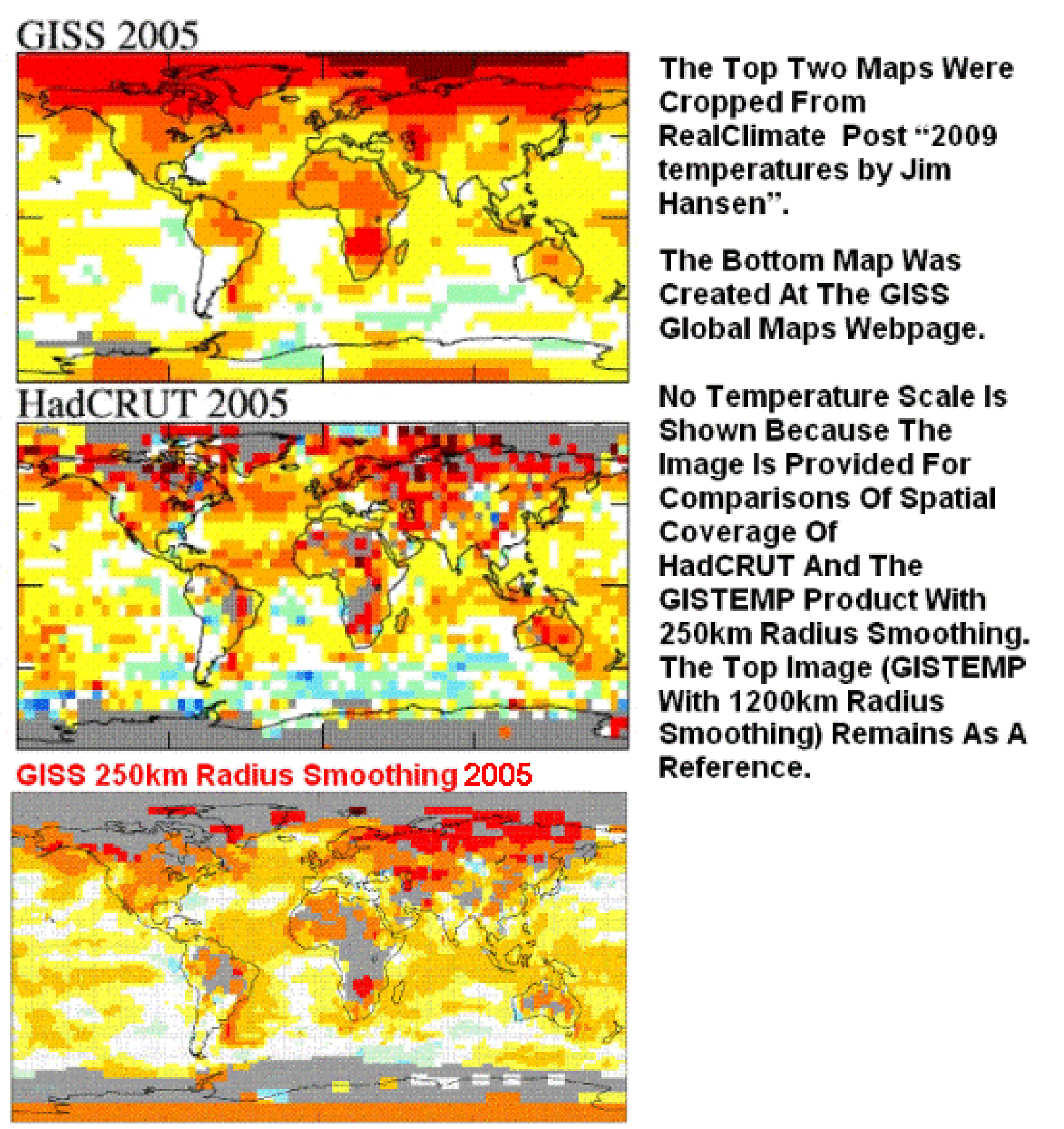
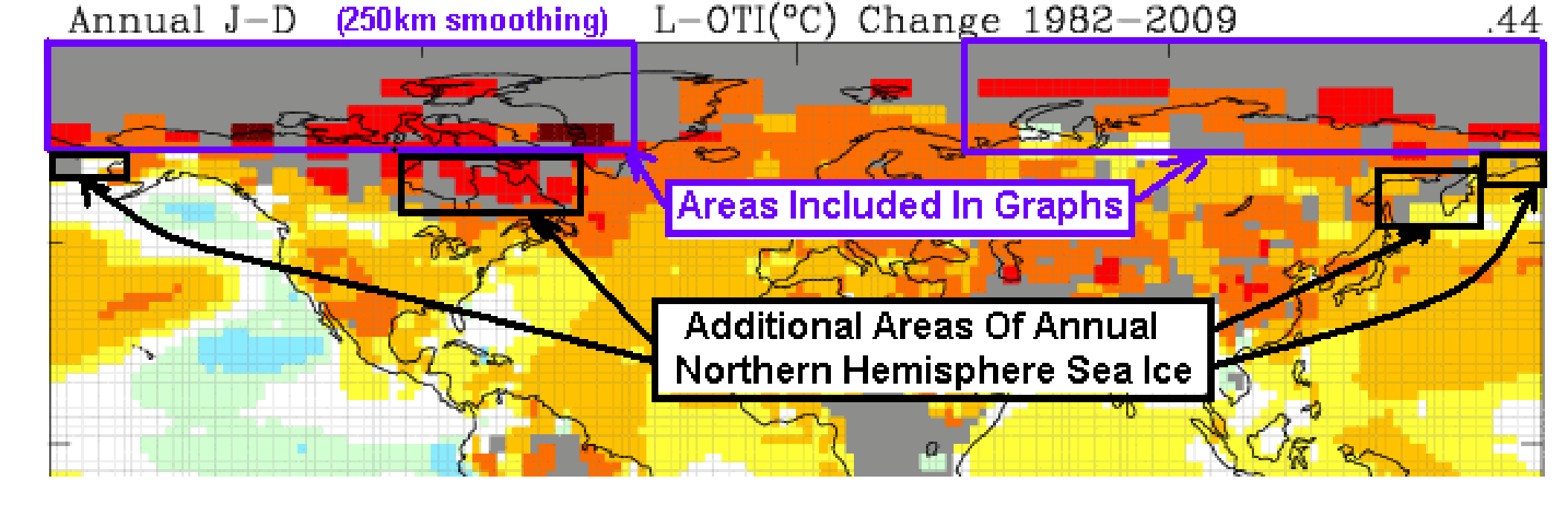
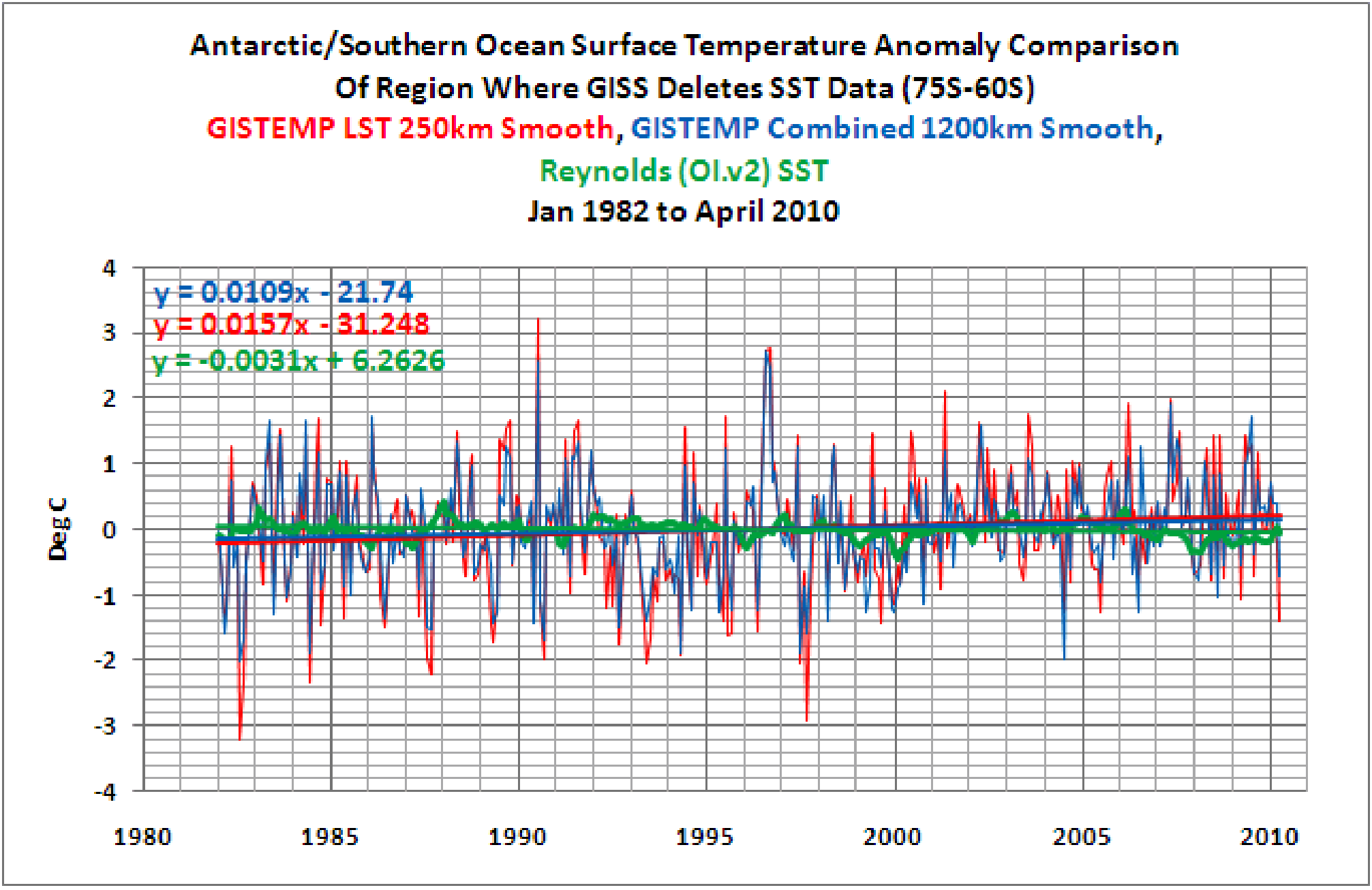
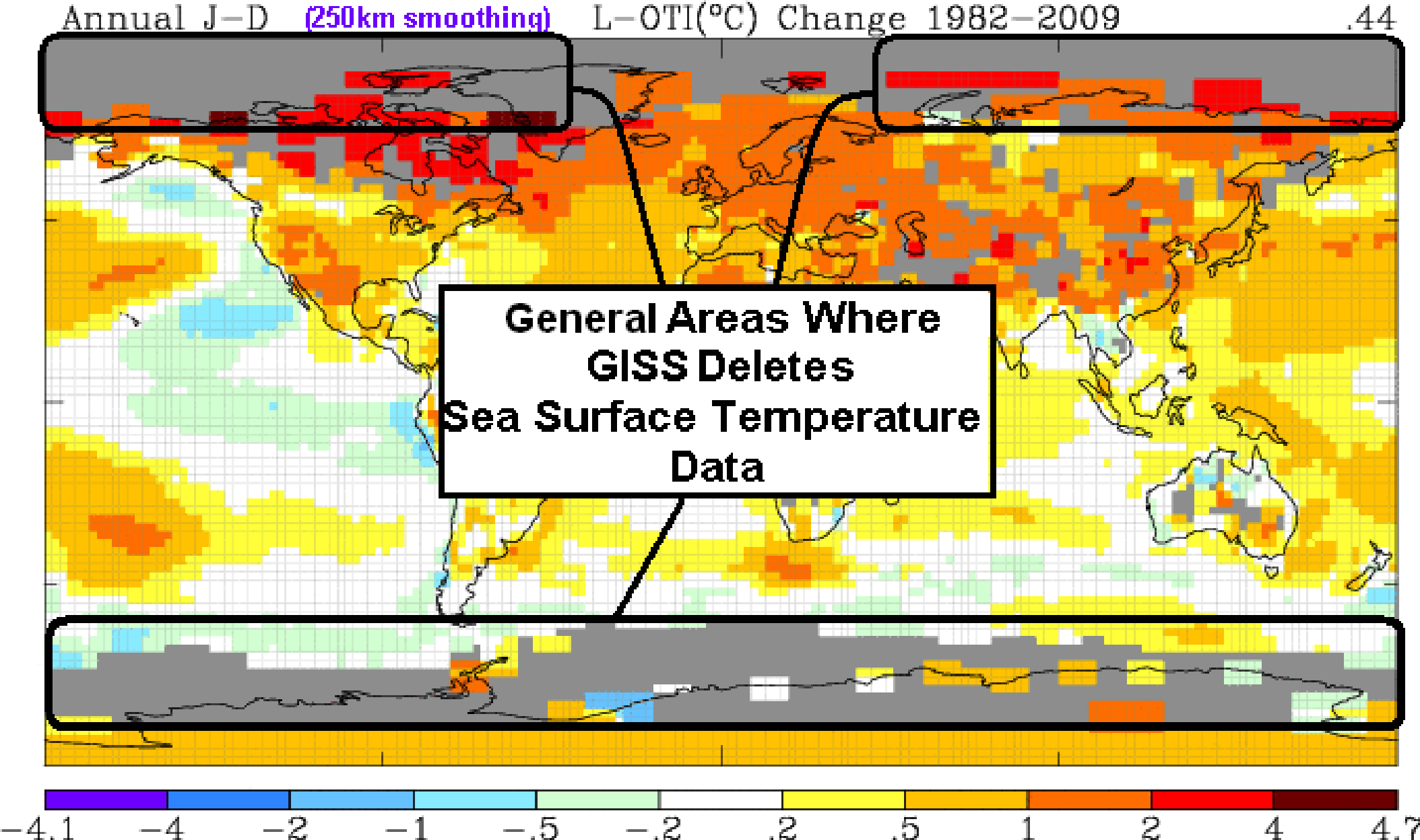                                                                                                                                                 > (in rot) Gebiete, in denen GISS allgemein Daten eliminiert.

In seinem Beitrag “unterschiedliche Ansichten” Diverging views auf Watts Up With That? hat Tilo Reber in der Current Analysis Website des GISS die folgende Feststellung gefunden:

„Gebiete, die nur gelegentlich mit Meereis bedeckt sind, werden hinter einer zeitunabhängigen Maske versteckt.“

Dies bedeutet, dass man zahlreiche Daten über die Anomalien der Wassertemperatur im Polarmeer und dem Südlichen Ozean aus den Aufzeichnungen von GISTEMP einfach entfernt hat. GISS hat nicht alle Daten entfernt, sondern nur diejenigen aus den Gebieten, in denen die jahreszeitliche Eisschmelze stattfindet. Dies ist jedoch in weiten Gebieten der Fall.

Ich habe nach einer Erklärung für den Ausschluss der Wassertemperaturdaten in den Papieren der GISTEMP references – Seite gesucht, aber keine gefunden.

Das Gebiet im Polarmeer, in dem GISS die Daten der Wassertemperatur nicht berücksichtigt

Abb. 3 zeigt vier Karten der Arktis (stereographische Projektionen, 65°N bis 90°N), die mit Hilfe eines Programms zur Kartenerstellung vom KNMI Klima-Explorer. [KNMI = Der Wetterdienst der Niederlande, A. d. Übers.] generiert wurden. Die Karten zeigen Temperaturanomalien und die Bedeckung mit Meereis für den Monat September 2005. Dieses Jahr wurde gewählt, weil es auch Gegenstand im Beitrag von Jim Hansen auf RealClimate ist, und dieser Monat, weil im September allgemein die minimale jahreszeitliche Eisbedeckung zu verzeichnen ist. Die Isothermen auf den Temperaturkarten wurden konstruiert, um die SST-Anomalien zu zeigen. Karte (a) zeigt die Ausdehnung des Meereises, abgeleitet aus den Reynolds (OI.v2)-Daten.

Die Daten der Meereisausdehnung wurden so skaliert, dass eisfreie Gebiete grau erscheinen. In den anderen Karten erscheinen Gebiete, aus denen keine Daten vorliegen, weiß. Karte (b) zeigt die SST-Anomalien, wie sie aus den Reynolds (OI.v2)-Daten der SST-Anomalien hervorgehen. GISS benutzt diese Daten seit Dezember 1981. Man kann leicht erkennen, dass aus den meisten Gebieten des Polarmeeres Daten vorliegen, wo immer das Abtauen des Meereises dies zulässt. Jedoch werden die meisten dieser Daten von GISS in der GISTEMP-Darstellung eliminiert. Dies wird ersichtlich in Karte (c), die die Temperaturanomalien in GISTEMP mit einem 250-km-Radius enthält. Die einzigen Daten bzgl. der SST-Anomalien stammen aus Gebieten nördlich des Nordatlantiks und Skandinaviens.

Alle anderen Daten wurden eliminiert!

Bei den farbigen Zellen über dem Ozean (z. B. nördlich von Sibirien und westlich von Nordwestgrönland) in Karte (c) handelt es sich um Daten von Landstationen, die bis auf das Polarmeer hinaus von GISS mit dem 250-km-Radius extrapoliert wurden. Und als Referenz zeigt Karte (d) eine „Kombination“ von Temperaturanomalien über Land und über Wasser. Dies ist die generelle Darstellung globaler Temperaturanomalien vom GISS. Die meisten Gebiete des Polarmeeres in Karte (d) sind rot gekennzeichnet, was mit einer Anomalie größer als 1 K identisch ist. Karte (b) zeigt ein wesentlich kleineres Gebiet mit erhöhten Werten der SST-Anomalie.

Abbildung 3

Im Grunde eliminiert GISS alle Daten aus dem Polarmeer zwischen 65°N und 90°N sowie, um runde Zahlen zu erhalten, zwischen 40°E und 40°W. In diesen Gebieten liegt ein großer Teil des Polarmeeres. Natürlich ist die Stärke der Auswirkungen abhängig von der Jahreszeit und hängt vom jahreszeitlichen Abschmelzen des Meereises ab. Die Eisausdehnung muss jährlich abnehmen, um die Wassertemperatur messen zu können.

Ich werde die oben genannten Koordinaten für die folgenden Beispiele verwenden, aber man beachte, dass Gebiete mit Eisbedeckung südlich von 65°N nicht berücksichtigt werden. Diese zusätzlichen Gebiete zeigt die Abb. 4. Es handelt sich beispielsweise um die Bering See, die Hudson Bay, die Baffin Bay und die Davis-Straße zwischen Grönland und Kanada sowie das Ochotskische Meer südwestlich der Halbinsel Kamtschatka.

Abb. 4  (violett): Gebiete, die in den Graphiken enthalten sind. (schwarz): Zusätzliche Gebiete mit jährlich auftretendem Meereis.

Beachte: GISS verwendet die Daten des Hadley Center HADISST als Quelle von SST-Daten von Januar 1880 bis November 1981 und NCDC Reynolds (OI.v2)-Daten von Dezember 1981 bis jetzt. Um die Notwendigkeit der Angleichung beider Datensätze zu umgehen, untersucht dieser Beitrag lediglich die Periode von 1982 bis heute. Und um sicherzustellen, dass die Kurven der Abb’n 3 und 6 nicht durch Unterschiede zwischen den GISTEMP-Daten und den Reynolds (OI.v2)-Daten, welche ohnehin erst seit November 1981 zur Verfügung stehen, verzerrt werden, habe ich den Zeitraum von 1982 bis 2009 als Basis für meine Untersuchungen gewählt.

Warum ist es so bedeutsam, Daten der Wassertemperatur durch Daten von Landstationen zu ersetzen?

Temperaturänderungen über Land sind viel größer als Änderungen der Wassertemperatur. Siehe dazu Abb. 5. Seit Januar 1982 ist der Trend der Temperaturanomalien über Land, ermittelt mit einem 250-km-Radius, etwa 8 mal höher ist als der Trend der Wassertemperatur für das gleiche Gebiet.

Der Trend der SST-Anomalie im Polarmeer beträgt linear etwa 0,082°C pro Jahrzehnt, während der gleiche Trend von Temperaturanomalien über Land o,68°C pro Jahrzehnt beträgt. Und als Referenz zeigt sich, dass der „kombinierte“ Trend arktischer Temperaturanomalien für dieses Gebiet 9 mal größer ist als der Trend der Wassertemperatur.


Abb. 5

Indem GISS die SST-Anomalien nicht berücksichtigt, verwendet es den Datensatz mit einer viel größeren Variation von Monat zu Monat und einem viel höheren Trend der Temperaturabweichung für seine Darstellung arktischer Temperaturanomalien. Offensichtlich verzerrt dies die „kombinierten“ Temperaturanomalien in diesem Gebiet.

GISS eliminiert auch die Werte der Wassertemperatur auf der Südhemisphäre

Abb. 6 zeigt vier Karten der Antarktis und der Südlichen Ozeane (stereographische Projektion, 90°S bis 60°S). Die Darstellung ist wie in Abb. 8 [dies steht so im Original. Gemeint ist aber vermutlich Abb. 3. A. d. Übers.]. Karte (b) zeigt die SST-Anomalien mit den Reynolds (OI.v2)-Daten der SST-Anomalie. Diese Daten überdecken den größten Teil der südlichen Ozeane, aber GISS lässt einen wesentlichen Teil davon einfach unter den Tisch fallen, wie Karte (c) zeigt. Übrig bleiben lediglich SST-Anomaliewerte in einigen nördlicher gelegenen Gebieten des Südlichen Ozeans. Dies sind Gebiete, die nicht „gelegentlich von Meereis bedeckt sind“.

Abb. 6

Abb. 7 zeigt folgende Temperaturanomalien für das Gebiet zwischen 75°S und 60°S:

-Wassertemperatur und
-Landtemperaturwerte aus der GISTEMP-Darstellung mit einem 250-km-Radius und
-kombinierte Land- und Wassertemperatur aus der GISTEMP-Darstellung mit einem 1200-km-Radius.

Die Variabilität der Temperatur über dem antarktischen Festland ist viel größer als die der Wassertemperatur in den südlichen Ozeanen. Der lineare Trend der SST-Anomalie  ist negativ, während derjenige der Landtemperaturen deutlich positiv ist. Daraus folgt: wenn man die Daten der Wassertemperatur in großen Gebieten der Südlichen Ozeane eliminiert (wie in Abb. 6 gezeigt) und sie durch Daten mit Werten vom Festland ersetzt, ergeben sich viel größere Werte der Temperaturanomalien während des Abschmelzens des Meereises.

Man beachte, dass die kombinierte Darstellung in GISTEMP einen niedrigeren Trend aufweist als die Landstationen für sich allein. Teilweise resultiert diese Abnahme des Trends aus dem Umstand, dass das gewählte breitenkreisparallele Band, das in diesem Vergleich betrachtet wird, immer noch Gebiete enthält, die von GISS nicht ausgeschlossen wurden (weil es zu keinen Veränderungen des Meereises kommt).

Abb. 7 Vergleich der SST-Anomalien der Südlichen Ozeane mit den Gebieten, in denen GISS die SST-Werte eliminiert.
GISTEMP mit 250-km-Radius, GISTEMP kombiniert mit 1200-km-Radius, Reynolds (OI.v2)

Die zonalen mittleren Graphen spiegeln den Grund für die Abweichungen bei GISS

Wenn man eine Karte auf der GISS Global Maps Website erstellt, erscheinen zwei Graphiken. Oben findet sich die Karte wie in Abb. 1 gezeigt, unten findet sich ein zonaler Graph. Dieser Graph repräsentiert die Temperaturanomalien entlang von Breitenkreisen, beginnend am Südpol bei 89°S und endend am Nordpol bei 89°N. Er illustriert die Änderungen (Anstieg und Fall) der mittleren zonalen Temperaturanomalien von 1982 bis 2009 aus der GISTEMP-Darstellung der kombinierten Land- und Wassertemperatur mit dem 1200-km-Radius. Die größte Änderung dieser Anomalien zeigt sich am Nordpol. Dies ist auf ein Phänomen zurückzuführen, das man Polare Amplifikation nennt.



Abb. 8 Beispiel eines Graphen der Anomalie der zonalen Mitteltemperatur nach GISS.

Das Beispiel zeigt die Änderungen der Temperatur von 1982 bis 2009 für die GISTEMP-Darstellung kombinierter Daten mit einem 1200-km-Radius.

Um einen Graphen analog der GISS-Darstellung zu konstruieren, habe ich die Darstellungen in GISTEMP mit dem 1200-km-Radius in 5°-Segmante zusammengefasst von 90°S bis 90°N für die Jahre 1982 bis 2009. Dann habe ich den Dekadentrend mit 2,8 multipliziert. Diesem Prozess unterzog ich auch die Daten von HADCRUT. Das Ergebnis zeigt Abb. 9

Die beiden Datensätze sind zwischen 50°S und 50°N sehr ähnlich, unterscheiden sich jedoch in Richtung der Pole. Wie in diesem Beitrag schon oft erwähnt, eliminiert GISS die Werte der Wassertemperatur in höheren Breiten (jenseits von 50°) und ersetzt sie durch Werte von Landstationen.


Abb. 9 Vergleich der mittleren zonalen Temperaturanomalie für Segmente von 5° geogr. Breite HADCRUT3, GISTEMP mit 1200-km-Radius
(Änderungen basierend auf dem linearen Trend)  Jan 1982 bis Dez. 2009

Abb. 10 zeigt die Unterschiede zwischen den Änderungen der zonalen mittleren Temperaturanomalien in GISTEMP und HADCRUT. Sie zeigt noch besser die Unterschiede in Gebieten, in denen GISS die Wassertemperaturen durch Werte von Landstationen ersetzt, die natürlich höhere lineare Trends in dieser Periode aufweisen.


Abb. 10 Vergleich der mittleren zonalen Temperaturanomalie für Segmente von 5° geogr. Breite GISTEMP mit 1200-km-Radius minus HADCRUT3 (Änderungen basierend auf dem linearen Trend)  Jan 1982 bis Dez. 2009 Unterschiede zeigen sich dort, wo GISS Wassertemperaturen wegfallen lässt

Bob Tisdale

Quelle

Karten und Daten der Meereisbedeckung können auf der Site des KNMI Climate Explorer eingesehen werden:
http://climexp.knmi.nl/selectfield_obs.cgi?someone@somewhere

Die Übersetzung besorgte Chris Frey EIKE

Der Artikel kann als pdf Datei abgerufen werden.

Related Files