rgbatduke sagt:
Wenn man sagt, dass wir einen bestimmten Zeitraum lang warten müssen, um zu der Schlussfolgerung zu gelangen, dass „die Modelle falsch sind“, ist das aus zwei Gründen gefährlich und falsch. Erstens – und dieser Punkt wird erstaunlich stark ignoriert – gibt es sehr viele verschiedene Modelle, die alle für sich in Anspruch nehmen, auf  der Physik zu basieren. Und doch ergeben keine  zwei von ihnen etwa die gleichen Ergebnisse!
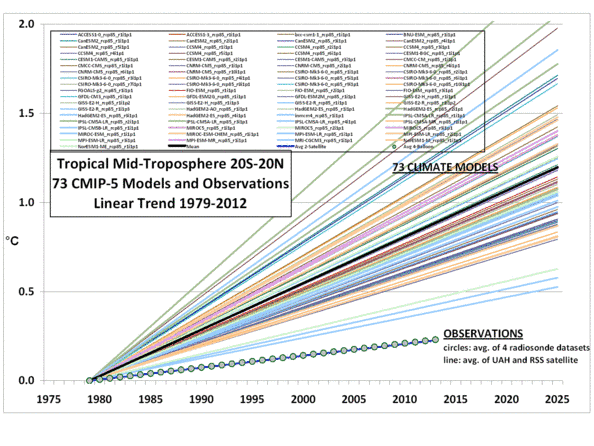
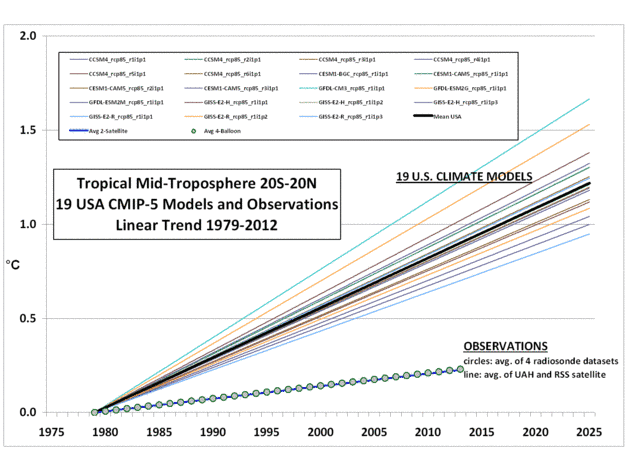
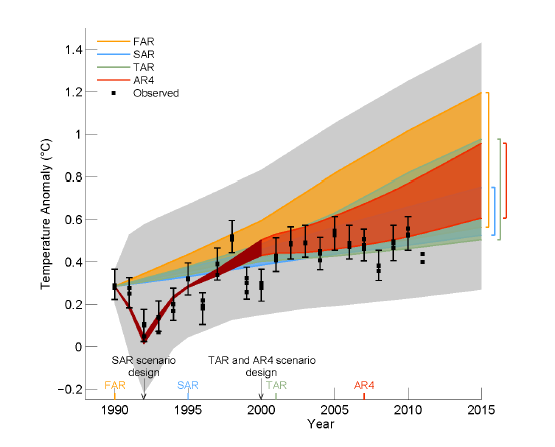
Dies spiegelt sich in den von Monckton veröffentlichten Graphiken, wobei die AR5-Trendlinie das Mittel all dieser Modelle ist. Trotz der Anzahl der hierzu beitragenden [Modelle] ist die Varianz gewaltig. Falls jemand einen „Spaghetti-Graphen“ der einzelnen Modellprojektionen veröffentlicht (wie es Roy Spencer kürzlich in einem anderen Beitrag getan hat), sieht er aus, wie das ausgefranste Ende eines Seiles und nicht wie eine kohärente Verteilung um ein bestimmtes, von der Physik gestütztes Ergebnis.
Man beachte den impliziten Schwindel in dieser Graphik. Wenn man ein Mittel und die Standardabweichung über die Modellprojektionen bildet und dann dieses Mittel als eine „sehr wahrscheinliche“ Projektion und die Varianz als repräsentativ für die Fehlerbandbreite darstellt, behandelt man die Differenzen zwischen den Modellen so, als ob sie nicht-korrelierte Zufallsvarianten wären, die sich in einer Abweichung um das wirkliche Mittel scharten.

Was soll denn das heißen?!

Es ist ein solch horrender Missbrauch von Statistik, dass man gar nicht so recht weiß, wo man am besten anfangen soll. Man möchte am liebsten dem Erzeuger dieser Graphik-Zusammenstellung – wer auch immer das war – eine runterhauen und dafür sorgen, dass diese Person niemals wieder etwas Wissenschaftliches oder Statistisches veröffentlicht. Man darf kein Ensemble unabhängiger und gleich verteilter Modelle erzeugen, die einen unterschiedlichen Code haben. Man kann eventuell ein einzelnes Modell erzeugen, das ein Ensemble von Vorhersagen erzeugt, indem man gleichartige Abweichungen (Zufallszahlen) verwendet, um „Rauschen“ (zur Repräsentation der Unsicherheit) in die Inputs mit eingehen zu lassen.
Was ich sagen möchte: die Varianz und das Mittel des „Ensembles” der Modelle ist vollständig bedeutungslos in statistischer Hinsicht, weil der Input nicht die wirklich grundlegenden Eigenschaften besitzt, die für eine bedeutungsvolle Interpretation erforderlich sind. Sie sind nicht unabhängig, ihre Unterschiede basieren nicht auf einer Zufallsverteilung von Fehlern, es gibt keinen wie auch immer gearteten Grund zu glauben, dass die Fehler oder Differenzen nicht auf Vorurteilen beruhten (unter der Voraussetzung, dass es nur eine einzige Möglichkeit für den Menschen gibt, etwas Vorurteilfreies zu erzeugen: nämlich die Verwendung eines Würfels oder anderer objektiver Zufallsgeneratoren).
Warum sollte man also diesen Unsinn hinnehmen und lineare Fits für eine Funktion – die globale Temperatur – anpassen, die niemals in ihrer gesamten Historie linear verlaufen ist, obwohl sie natürlich immer annähernd so glatt war, dass man jederzeit eine Taylor-Reihe in hinreichend kleinen Intervallen erzeugen und einen linearen Term erhalten kann, der – durch die Natur von Taylor-Reihen-Fits an nichtlinearen Funktionen – garantiert scheitern wird, wenn er extrapoliert wird, weil nichtlineare Terme höherer Ordnung sich draufsetzen und die Herrschaft übernehmen? Warum sollte man ein Lippenbekenntnis abgeben für die Vorstellung, dass R² oder p für eine lineare Anpassung oder für einen Kolmogorov-Smirnov-Vergleich der realen Temperaturaufzeichnung mit der extrapolierten Modellvorhersage irgendeine Bedeutung hätten? Sie haben keine.
Noch einmal: Es ergibt keine Bedeutung! Und ist unhaltbar in Theorie und Praxis der statistischen Analyse. Genauso könnte man ein Hexenbrett nehmen [siehe hier bei wikipedia, Bild oben rechts] als Basis für Behauptungen über die Zukunft des Klimas, und zwar als Ensemble-Mittel unterschiedlicher berechneter physikalischer Modelle, die sich nicht durch wirklich zufällige Variationen unterscheiden und die allen Arten von ausgelassenen Variablen unterworfen sind, dazu ausgewählten Variablen, der Implementierung und vorurteilsbefangener Initialisierung. Das Brett könnte uns die richtige Antwort liefern oder auch nicht, außer, dass es Glück bringen kann bei der Begründung einer Antwort auf irgendeiner vernünftigen Grundlage.
Wir wollen diesen Prozess einmal umkehren und tatsächlich die Verteilung der Modellergebnisse einer statistische Analyse unterwerfen. Zur Erinnerung: es geht um die Behauptung, dass sie alle nach den gültigen Gesetze der Physik korrekt implementiert sind. Zum Beispiel, wenn ich versuche, eine a priori-Berechnung der Feinstruktur – sagen wir – eines Kohlenstoff-Atoms durchzuführen, könnte ich damit so beginnen, dass ich ein Einzel-Elektronenmodell auflöse, wobei ich die Wechselwirkung zwischen den Elektronen unter Verwendung der Wahrscheinlichkeits-Verteilung des Einzel-Elektronenmodells bestimme, um eine sphärisch symmetrische „Dichte“ von Elektronen um den Kern zu erzeugen. Dann stelle ich eine in sich widerspruchsfreie Wiederholungs-Feldtheorie-Iteration auf  (indem ich das Einzel-Elektronenmodell für das neue Potential auflöse) bis es konvergiert. (Das ist als „Hartree-Approximation bekannt“).
Nun könnte jemand sagen „Moment mal, das ignoriert das Pauli-Ausschlußprinzip [Pauli exclusion principle]“ sowie die Forderung auf vollkommene Antisymmetrie der Elektronen-Wellenfunktion. Man könnte dann das (immer noch Einzel-Elektronen-)Modell komplizierter machen und eine Slater-Determinante [?] konstruieren, die man als vollständig antisymmetrische Repräsentation der Elektronen-Wellenfunktionen verwendet; sodann die Dichte erzeugen und die widerspruchsfreie Feldberechnung zur Konvergenz durchführen (das ist Hartree-Fock).
Jemand anders könnte dann darauf hinweisen, dass dies immer noch die „Korrelations-Energie“ des Systems unterschätze, weil das Behandeln der Elektronenwolke als kontinuierliche Verteilung die Tatsache ignoriert, dass einzelne Elektronen sich stark abstoßen und folglich nicht in die Nähe eines anderen kommen wollen. Beide frühere Herangehensweisen unterschätzen die Größe des Elektronen-Loches und machen das Atom folglich „zu klein“ und „zu stark gebunden“. Eine Palette von Schemata wird zur Behandlung dieses Problems vorgeschlagen – wobei die Verwendung einer semi-empirischen lokalen Dichtefunktion das wahrscheinlich erfolgreichste ist.
Und noch jemand könnte dann anmerken, dass das Universum wirklich relativistisch ist, und dass wir beim Ignorieren der Relativitätstheorie und der Durchführung einer klassischen Berechnung einen Fehler einführen in alles oben Gesagte (obwohl es in das halb empirische LDF-Verfahren heuristisch eingebracht werden kann).
Am Ende könnte man sehr gut ein „Ensemble” von Modellergebnissen in der Hand haben, die alle auf der Physik basieren. Tatsächlich basieren auch die Unterschiede auf der Physik. Die  von einem Versuch zum nächsten weggelassene Physik, oder die zur Annäherung und zur Einbringung der Physik verwendeten Methoden, können wir nicht in eine Berechnung der Grund-Prinzipien einschließen (man beachte, wie ich mit der LDF eine semi-empirische Note eingeschmuggelt habe, obwohl man Dichtefunktionen aus den Grund-Prinzipien ableiten kann (z B. Thomas-Fermi-Approximation), die normalerweise nicht besonders gut sind, weil sie nicht im gesamten Bereich der in wirklichen Atomen beobachteten Dichte gültig sind). Was ich hervorheben möchte, die Durchführung der präzisen Berechnung ist keine Option. Wir können das Vielkörperproblem in der Quantentheorie nicht mehr exakt lösen, wie wir auch nicht mehr das Vielkörperproblem in der klassischen Theorie exakt lösen können, auch nicht den Satz von offenen, nicht-linearen, gekoppelten, gedämpften, angetriebenen Navier-Stokes-Gleichungen in einem nicht-inertialen Bezugsrahmen, wie es das Klimasystem darstellt.
Wohlgemerkt: die Lösung der exakten, vollständig korrelierten, nichtlinearen Elektronen-Wellenfunktion des einfachen Kohlenstoffatoms – oder des weitaus komplexeren Uranatoms – ist trivial einfach (hinsichtlich der Berechnung) im Vergleich zum Klimaproblem. Wir können beides nicht berechnen, aber wir können einer konsistenten Annäherung an die Lösung von Ersterem viel näher kommen als bei Letzterem.
Sollten wir also das Ensemble-Mittel von „physikalisch fundierten” Modellen heranziehen, um die Quanten-Elektron-Struktur eines Kohlenstoffatoms zu bestimmen und dieses als die beste Vorhersage der Kohlenstoff-Quantenstruktur ansehen?
Nur wenn wir sehr dumm, oder geisteskrank sind, oder etwas glauben machen wollen. Wenn man das von mir Gesagte sorgfältig liest (was Sie vielleicht nicht getan haben – man überliest vieles, wenn ein Jahr oder mehr an Elektronen-Quantentheorie in einigen Sätzen zusammengefasst wird, dabei habe ich noch die Perturbations-Theorie, die Feynman-Diagramme usw. ausgelassen), merkt man, dass ich geschummelt habe – ich bin in eine semi-empirische Methode geraten.
Wer wird gewinnen? LDF natürlich. Warum? Weil die Parameter so angepasst sind, dass dabei der beste Fit für das wirkliche empirische Spektrum von Kohlenstoff herauskommt. Alle anderen unterschätzen das Korrelations-Loch, die Fehler werden systematisch vom korrekten Spektrum abweichen. Ihr Mittel wird systematisch abweichen. Durch die Gewichtung von Hartree (dümmster vernünftiger „auf der Physik beruhender Ansatz“) in gleichem Maße wie wie LDF beim „Ensemble“-Mittel wird garantiert, dass der Fehler in diesem „Mittel“ signifikant sein wird.
Nehmen wir mal an, wir wüssten nicht (ganz so, wie wir mal nicht wussten), welches Modell die besten Ergebnisse brächte. Nehmen wir weiter an, dass niemand das Spektrum von Kohlenstoff wirklich gemessen hätte, so dass dessen empirische Quantenstruktur unbekannt wäre. Wäre das Ensemble-Mittel dann sinnvoll? Natürlich nicht. Ich habe die Modelle in der Weise präsentiert, wie die Physik selbst eine Verbesserung vorhersagt – und habe später wichtige Details hinzugefügt, die von Hartree ausgelassen wurden. Man kann nicht sicher sein, dass das nachträgliche Hinzufügen dieser Details die Dinge wirklich verbessert, weil es immer möglich ist, dass die Korrekturen nicht monoton sind (und tatsächlich sind sie es in höheren Größenordnungen der Perturbations-Theorie mit Nahezu-Sicherheit nicht). Und doch würde niemand so tun, als sei das Mittel aus einer Theorie und einer verbesserten Theorie  „wahrscheinlich“ besser als die verbesserte Theorie selbst, weil das sinnlos wäre. Auch würde niemand behaupten, dass Ergebnisse der diagrammatischen Perturbations-Theorie notwendigerweise semi-heuristische Methoden wie LDF in den Schatten stellen könnten, weil das oft genug nicht der Fall ist.
Was man in der realen Welt tun würde wäre: das Spektrum von Kohlenstoff messen, dies mit den Vorhersagen des Modells vergleichen und erst dann dem Gewinner den Siegerkranz aushändigen. Niemals umgekehrt. Und da keiner der Gewinner exakt sein wird – tatsächlich war trotz jahrzehntelanger Forschung keiner der Gewinner auch nur in der Nähe beobachteter/gemessener Spektren, trotz des Gebrauchs von Supercomputern für die Berechnungen (zugegeben, die waren damals langsamer als Ihr Mobiltelefon heute) – würde man dann dennoch zurück am Zeichenbrett und der Eingabe-Konsole versuchen, es besser zu machen?
Können wir diese Art sorgfältigen Nachdenkens auf den Spaghetti-Knoten der GCMs und ihrer erheblich divergierenden Lösungen anwenden? Natürlich können wir das! Zuerst sollten wir aufhören so zu tun, als ob das „Ensemble“-Mittel und die Varianz irgendeine Bedeutung hätten und sie einfach nicht mehr berechnen. Warum sollte man eine bedeutungslose Zahl ausberechnen? Zweitens könnten wir wirkliche Klimaaufzeichnungen von einem beliebigen „Epochen-Startpunkt“ nehmen – der Startpunkt spielt langfristig keine Rolle, wir müssen den Vergleich über einen langen Zeitraum durchführen, weil für jeden beliebigen kurzen Zeitraum  von einem beliebigen Startpunkt aus ein vielartiges Rauschen die systematischen Fehler verschleiert – und wir können nur die Realität mit den Modellen vergleichen. Wir können dann die Modelle aussortieren, indem wir (mal angenommen) alle außer den oberen fünf in eine Art von „Fehler-Papierkorb“ legen und sie nicht mehr für irgendeine Art Analyse oder politische Entscheidungsprozesse heranzuziehen, es sei denn, sie fangen an, sich mit der Wirklichkeit zu vertragen.
Danach könnten sich echte Wissenschaftler hinsetzen und die fünf Gewinner betrachten – und darüber nachdenken, was sie zu Gewinnern gemacht hat – was sie dazu gebracht hat, der Realität am nächsten zu kommen – und den Versuch machen, sie noch besser zu machen. Zum Beispiel, wenn sie weit oben rangieren und von den empirischen Daten divergieren, könnte man überlegen, früher nicht beachtete physikalische Phänomene hinzuzufügen, semi-empirische oder heuristische Korrekturen oder Input-Parameter anzupassen, um den Fit zu verbessern.
Dann kommt der schwierige Teil – Abwarten. Das Klima ist nicht so einfach gebaut wie ein Kohlenstoffatom. Das Spektrum von Letzterem ändert sich nie, es ist immer gleich. Ersteres ist niemals gleich. Entweder ein dynamisches Modell ist niemals das Gleiche und spiegelt die Variationen der Realität, oder man muss sich damit abfinden, dass das Problem ungelöst und die unterstellte Physik falsch ist, wie „wohlbekannt“ auch immer diese Physik ist. Also muss man abwarten und sehen, ob ein Modell, das adjustiert und verbessert worden ist und das auf die Vergangenheit bis zur Gegenwart besser passt, tatsächlich einen Vorhersage-Wert hat.
Am schlimmsten ist, dass man nicht einfach mit Statistik entscheiden kann, wann und warum Vorhersagen scheitern, weil das verdammte Klima nicht-linear ist, nicht-Markovianisch, stattdessen chaotisch und offensichtlich auf nichttriviale Weise beeinflusst ist von einem globalen Wettbewerb von gegensätzlichen und manchmal sich aufhebenden, kaum verstandenen Faktoren: Ruß, Aerosole, Treibhausgase, Wolken, Eis. Dekadische Oszillationen, Störungen, entstanden aus dem chaotischen Prozess, die globale, anhaltende Änderungen der atmosphärischen Zirkulation auf lokaler Basis verursachen (z. B. blockierende Hochdruckgebiete über dem Atlantik, die dort ein halbes Jahr lang liegen bleiben). Diese Änderungen haben gewaltige Auswirkungen auf jährliche oder monatliche Temperaturen, Regenmengen und so weiter. Dazu orbitale Faktoren, solare Faktoren. Änderungen der Zusammensetzung der Troposphäre, der Stratosphäre, der Thermosphäre. Vulkane. Änderungen bei der Landnutzung. Algenblüten.
Und dann dieser verdammte Schmetterling. Jemand muss dieses blöde Ding zerquetschen, weil der Versuch, ein Ensemble aus einer kleine Stichprobe aus einem chaotischen System zu mitteln, so dumm ist, dass ich mich gar nicht damit befassen kann. Alles ist gut, solange man über ein Intervall mittelt, das kurz genug ist, um an einen bestimmten Attraktor gebunden zu sein, der schwingt und alles vorhersagbar macht – und dann mit einem Male ändern sich die Attraktoren und alles mit ihnen! All die kostbaren Parameter, empirisch fein eingestellt auf den alten Attraktor müssen nun durch neue Werte ersetzt werden.
Das ist der Grund, warum es tatsächlich unsinnig ist, der Vorstellung zuzustimmen, dass irgendeine Art p-Werte oder R², der aus irgendeinem Mittel im AR 5 abgeleitet ist, irgendeine Bedeutung hätte. Diese Vorstellung verliert ihren hohen Stellenwert (sogar dann noch, wenn man in guter Absicht zu argumentieren versucht, dass dieses „Ensemble“ elementare statistische Tests nicht bestünde). Statistisches Testen ist eine wahrhaft wackelige Theorie, offen für Datenmanipulation und horrende Fehler, vor allem, wenn sie von zugrunde liegenden IID-Prozessen [Independent and identically distributed processes] gesteuert wird („grüne Bohnen verursachen Akne“). Man kann nicht naiv ein Kriterium anwenden, wie z. B. „falsch, wenn P < 0,05“, und all das bedeutet im günstigsten Fall, dass die gegenwärtigen Beobachtungen unwahrscheinlich sind bei einer gegebenen Null-Hypothese von 19 zu 1. Auf solchem Niveau verlieren und gewinnen Spieler immer wieder ihrer Wetten.
Also möchte ich empfehlen – in aller Bescheidenheit – , dass die Skeptiker weiter hart bleiben, sich nicht auf dieses Feld locken lassen und durch Diskussionen über Fragen ablenken lassen, wie z. B. warum die Modelle in so erschreckender Weise untereinander abweichen, selbst wenn man sie auf identische Spiel-Probleme anwendet, die viel einfacher sind als die wirkliche Erde. Und ich möchte empfehlen, dass wir empirische Beweise nutzen (es werden immer mehr), um gescheiterte Modelle zurückzuweisen, und dass wir uns auf diejenigen konzentrieren, die der Realität am nächsten kommen. Dabei darf man keine Modelle benutzen, die offensichtlich überhaupt nicht funktionieren, und vor allem keine mit irgendwelchen Arten von Vorhersagen „durchschnittlicher“ zukünftiger Erwärmung …
Bei meiner verhältnismäßigen Ignoranz würde es mich fünf Minuten kosten, alle GCMs außer den besten 10 Prozent auszusortieren (auch diese divergieren noch hinsichtlich der empirischen Daten, liegen jedoch noch innerhalb der erwarteten Fluktuation des Datensatzes). Dann würde ich den Rest aufteilen in eine obere Hälfte mit den Modellen, die man eventuell behalten und möglicherweise verbessern könnte, und in eine zweite Hälfte, deren weitere Verwendung ich für Zeitverschwendung halte. Das würde sie natürlich nicht zum Verschwinden bringen, aber in die Mottenkiste. Falls sich das zukünftige Klima jemals magischerweise dazu aufraffen sollte, zu den Modellen zu passen, wäre es nur eine Frage weniger Sekunden, sie wieder hervorzuholen und zu benutzen.
Natürlich, wenn man das tut, fällt die von den GCMs vorhergesagte Klimasensitivität von den statistisch betrügerischen 2,5°C pro Jahrhundert auf einen wesentlich plausibleren und möglicherweise immer noch falschen Wert von etwa 1°C pro Jahrhundert. Dieser Wert – Überraschung! – stellt mehr oder weniger eine Fortsetzung des Erwärmungstrends nach der Kleinen Eiszeit dar mit einem möglicherweise kleinen anthropogenen Beitrag. Diese große Änderung würde zu einem großen Aufruhr führen, weil die Leute merken würden, wie sehr sie von einer kleinen Gruppe von Wissenschaftlern und Politikern ausgenutzt worden sind, wie stark sie Opfer von unhaltbarem statistischen Missbrauch geworden sind, indem man ihnen suggeriert hat, dass sie alle stimmen mit gewissen Unterschieden an den Rändern.
Link: http://wattsupwiththat.com/2013/06/18/the-ensemble-of-models-is-completely-meaningless-statistically/
Übersetzt von Chris Frey EIKE unter Mithilfe von Helmut Jäger