Bevorzugen Google und Co bestimmte Webseiten bei „Suche nach“? – ein eigener Test

geschrieben von Andreas Demmig | 21. September 2018

Lesen sie unten wie ich getestet habe. Bestimmt gibt es einige unserer Leser die das nachvollziehen. Ich freue mich, von Ihren Ergebnisse lesen zu können.

Beginnen möchte ich noch mit Gedanken zum (übersetztem) Beitrag von WUWT:

Durchgesickerte Information zeigt Googles politische Einflussnahme in einem internen Video

… In diesem durchgesickerten Video von 2016 können wir die Bestürzung der Google-Führung über die Ergebnisse der US-Wahlen sehen und hören, wie sie ihre Verschwörung diskutieren, um einer Partei „Sachdienstleistungen“ für ihre politische Bemühungen zu ermöglichen, das Ergebnis zu beeinflussen.

Zitat Ende

 

Meine Gedanken:

Auf dem der Öffentlichkeit zugespieltem Video ist „eingeklingt“: CONFIDENTIAL – INTERNAL ONLY (vertraulich, nur intern).

Mich wundert, dass man diese interne Veranstaltung überhaupt gefilmt hat. Auf der anderen Seite schließe ich daraus, dass die Google Führung keinerlei Unrechtsbewusstsein (mehr?) hat – man wähnt sich auf der Seite der Guten.

Google stellt gute Webtools zur Verfügung, sonst hätte Google nicht weltweit so viel Erfolg – und bietet diese meist kostenlos zur Nutzung. Google ist jedoch keine staatlich finanzierte Heilsarmee, sondern verdient sein Geld mit Informationen, und das nicht zu knapp. Wer also Google nutzt, sollte sich darüber im Klaren sein. Jedoch, wenn ich etwas suche, entscheide ich selbst, was ich lese und was nicht.

Wesentlich kritischer bin ich gegenüber den vielen „Sicherheits-“ Updates, um die ein PC Nutzer nicht drumrum kommt. Wissen Sie, was Ihnen da untergeschoben wird? Entwickler bauen sich doch meist / immer ein Hintertürchen zum Testen und Zugang ein. Ausserdem, was rödelt die Festplatte meines PCs so emsig vor sich hin?

Zurück zu den Suchmaschinen.

WUWT empfahl alternative Suchmaschinen:

Zum Suchen empfehle ich DuckDuckGo und Mojeek . Von den beiden ist Mojeek meiner Meinung nach das bessere Tool, da es keine Google-orientierte Indexierungsbibliothek verwendet.
Zitat Ende

Ob diese  vom Autor genannten anderen Anbieter auch für uns in Deutschland besser sind, will ich mal testen. Klar ist, auch diese wollen / müssen Geld verdienen.

 

Test

Ich habe einfach mal nur „Eike“ eingegeben, um nach unserer Webseite zu suchen: in Mojeek, in DuckDuckGo, (weil von WUWT genannt) in Google, und in MS Edge. Unten die Ergebnisse – in anderer Reihenfolge – Die Ergebnisse haben mich überrascht. Bitte selbst einmal probieren.

  • DuckDuckGO

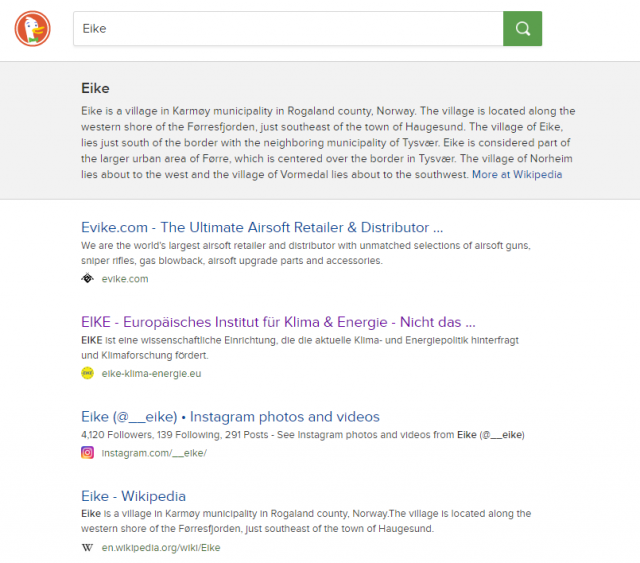
DuckDuckGo – Eike gleich auf der ersten Seite, an zweiter Position

 

  • Google

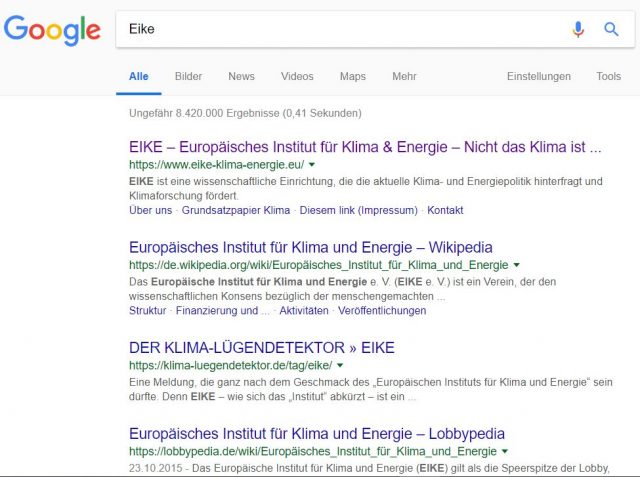
Eike gleich auf erster Seite, erste Position, danach Gegenstimmen

 

  • MS Edge

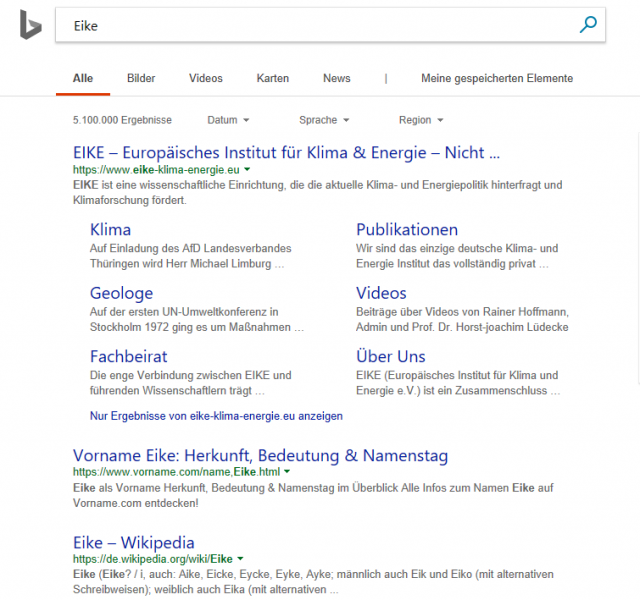
Eike gleich auf erster Seite, erste Position, danach Eigenamen „Eike“

 

  • Mojeek 

Beginn mit Eigennamen, Webseiten zu Eike erstmalig auf Seite 3, Beitrag einer AGW Seite vom Bund „Freunde der Erde“ mit einem Pamphlet gegen Eike
http://www.bund-rvso.de/eike-europaeisches-institut-fuer-klima-und-energie.html

weiter unten, immer noch Seite 3

ein Beitrag der AGW Seite von MITWELT, ebenfalls gegen Eike

http://www.mitwelt.org/eike-europaeisches-institut-klima-energie.html

 

Dann sind wir auf Seite 55, mit der AGW Seite DER Klima-Lügendetektor

Ich habe durchgehalten bis Seite 100, noch ein paar AGWs, aber Eike – Klima und Energie – nicht zu finden.

Weil ich mich gewundert habe, dass unser Eike nicht auftaucht, nur Eike-Gegner gezeigt werden, hier eine Erweiterung der Suchbegriffe:

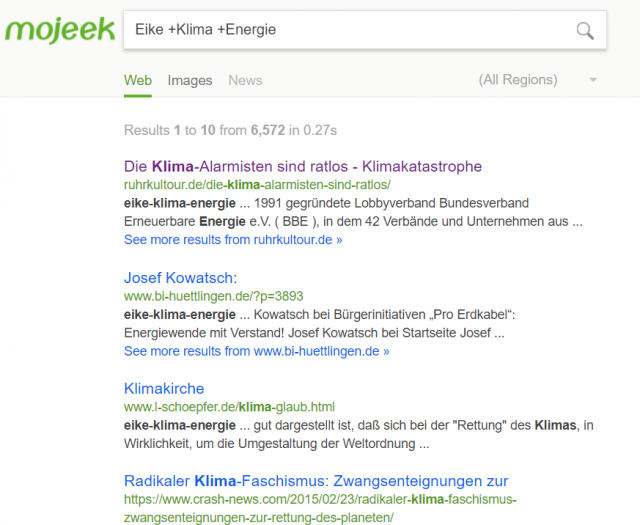
Es beginnt auf Seite 1 mit „Skeptikern“ (s.o.), bis Seite 25 bin ich gekommen, EIKE – Europäisches Institut für Klima & Energie gibt es nicht.

*** Jetzt aber mit mehr Begriffen

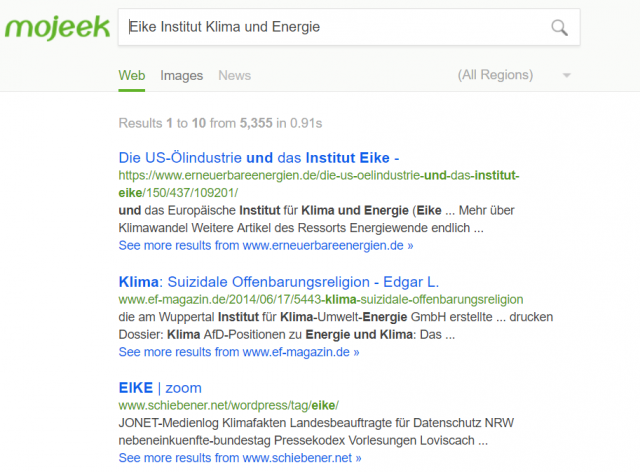
Was soll ich sagen, kein „unser Eike“. Auch mit diesen Suchbegriffen nicht: „Eike – Europäisches Institut Klima und Energie“

Wieder die weiteren Seite anzuschauen, ob nicht evtl. doch .. habe ich mir erspart.

Mein persönliches Fazit:

Aus meiner Sicht kann ich die Empfehlung von Mojeek nicht nachvollziehen.

Ich persönlich nutze Chrome und Google und Opera für VPN (… fremde Länder-Sperre) und habe bislang noch keine Probleme bzw. Einseitigkeit bemerkt.

Mit MS-IE oder Edge habe ich es auch probiert: Trivilal, es werden nicht immer alle „Felder“ einer Formularseite angezeigt (Schlamperei, bestimmt keine Beeinflussung). Auch kann (konnte) ich z.B. keine Webseite kopieren, damit ich sie in Word vor mir zum Übersetzen habe.

Richtig „persönliche Dinge“, wie z.B. meine Steuerklärung, speichere und bearbeite ich auf USB-Stick, der ansonsten nicht eingesteckt ist.

Ich wünsche Ihnen ein gutes Arbeiten mit Ihrem PC und kein Virus

Andreas Demmig

***



Durchgesickerte Information zeigt Googles Willen zur politischen Einflussnahme

geschrieben von Andreas Demmig | 21. September 2018

Auf WUWT wurde bereits darüber gesprochen, wie Google Klimaskeptiker aktiv unterdrückt unter Druck setzt.

Das Geschäftsmotto für Google war einmal: „Sei nicht böse ! „, Siehe unten, wie von der Wayback Machine am 21. April 2018 archiviert :

„Sei nicht böse.“ Die Googler wenden diese Wörter im Allgemeinen darauf an, wie wir unseren Nutzern dienen. Aber „Sei nicht böse“ ist viel mehr als das. Ja, es geht darum, unseren Nutzern unvoreingenommenen Zugang zu Informationen zu bieten, sich auf ihre Bedürfnisse zu konzentrieren und ihnen die bestmöglichen Produkte und Dienstleistungen zu bieten. Aber es geht auch darum, das Richtige allgemein zu tun – dem Gesetz zu folgen, ehrenvoll zu handeln und Kollegen mit Höflichkeit und Respekt zu behandeln.

Der Google-Verhaltenskodex ist eine der Methoden, mit denen wir „Sei nicht böse“ in die Praxis umsetzen. Es basiert auf der Erkenntnis, dass alles, was wir in Verbindung mit unserer Arbeit bei Google tun, an den höchstmöglichen Standards ethischen Geschäftsverhaltens gemessen wird und gemessen werden sollte. Wir setzen die Messlatte sowohl aus praktischen als auch aus aufsichtsrechtlichen Gründen hoch: Unser Engagement für höchste Standards hilft uns, großartige Mitarbeiter einzustellen, großartige Produkte zu entwickeln und loyale Nutzer zu gewinnen. Vertrauen und gegenseitiger Respekt zwischen Mitarbeitern und Nutzern sind die Grundlage unseres Erfolgs und müssen täglich verdient werden.

Dann, in erstaunlicher Wendung ihrer selbst, entfernten sie den Satz von ihrer Website und gaben sich selbst eine Lizenz, der dunklen Seite zu folgen.

Vielleicht haben Sie schon von dem internen „privaten“ Google-Video (das direkt nach der Präsidentschaftswahl 2016 entstanden ist) erfahren, das zu Breitbart gelangt ist. Es war nie beabsichtigt, dass die Öffentlichkeit es sieht, wir haben es jedoch. Nachdem Trump die Wahl gewonnen hat, zeigt das Video, wie das Google-Managementteam sich gegenseitig tröstet, umarmt, Tränen vergießt und darüber klagt, wie Trump gewonnen hat und Hillary Unrecht getan wurde.

Es ist ziemlich aufschlussreich. In dem Video haben wir den Chief Executive Officer, den Chief Financial Officer, zwei Vizepräsidenten und die beiden Männer, die 1998 Google gegründet haben. Sergey Brin und Larry Page.

In diesem durchgesickerten Video von 2016 können wir die Bestürzung der Google-Führung über die Ergebnisse der US-Wahlen sehen und hören, wie sie ihre Verschwörung diskutieren, um einer Partei „Sachdienstleistungen“ für ihre politische Bemühungen zu ermöglichen, das Ergebnis zu beeinflussen.

Die in diesem Video geäußerten Meinungen sind meiner Meinung nach empörend. Im Grunde genommen halten die Google-Manager die amerikanischen Wähler, die Trump gewählt hatten, als irrational, ausländerfeindlich, faul und dumm an. Brin vertritt die Meinung, dass Trump-Wähler aus „Langeweile“ gehandelt haben, was, wie er sagt, in der Vergangenheit einer der Faktoren war, die zu Faschismus und Kommunismus führten.

Google hat später eine Entgegnung veröffentlicht , in der es heißt, dass (in dem Video) nur einige Mitarbeiter und Führungskräfte ihre persönliche Meinung zum Ausdruck brachten: “ Seit 20 Jahren kann bei Google jeder seine Meinung frei äußern. „

In ihrer Entgegnung behauptet Google, dass nichts, was diese Führungskräfte in diesem Video sagten, eine politische Voreingenommenheit in ihren (Google-) Produkten nahelegt.

Das nehme ich ihnen nicht ab, nicht ein bisschen.

Die Google Finanzchefin in diesem Video, Ruth Porat, ist ein perfektes Beispiel. Sie wird hoch emotional, ihr kommen die Tränen und sie redet über den Moment, als sie realisierte, dass die Wahl „… in die falsche Richtung “ ging und dann erkannte sie das erste Mal “ WIR werden verlieren. Es ist wie eine „tonnenschwere Last“.

Später in dem Video fragt der Google-Mitbegründer Sergey Brin, was er tun kann, um eine „bessere Qualität der Regierungsführung und der Entscheidungsfindung“ zu.

Einschub: Google HAT NICHTS MIT REGIERUNGSENTSCHEIDUNGEN ZU TUN. Wenn Brin vorschlägt, dass sie eine „bessere Qualität“ sicherstellen müssen, ist das eine stillschweigende Anerkennung ihrer Voreingenommenheit, in einer Weise zu agieren, die sie für richtig halten.

Hier einige Auszüge aus der Geschichte von Breitbart:

THE GOOGLE TAPE: Google Co-Founder Sergey Brin ‘Deeply Offended’ by Trump’s Election
[Google-Mitbegründer Sergey Brin ist „tief beleidigt“ durch die Wahl von Trump]

Allum Bokhari, Breitbart

Sergey Brin, Mitbegründer eines der einflussreichsten Unternehmen der Welt:

„Als Einwanderer und Flüchtling finde ich diese Wahl zutiefst beleidigend, und ich weiß, dass viele von Ihnen das auch tun.“

Walker sagt, dass Google kämpfen sollte, um sicherzustellen, dass die populistische Bewegung – nicht nur in den USA, sondern auf der ganzen Welt – nur ein „Pieps“ und ein „Schluckauf“ in einem historischen Bogen bleiben, der sich dem Fortschritt zuwendet.

CEO Sundar Pichai erklärt, dass das Unternehmen maschinelles Lernen und künstliche Intelligenz entwickeln wird, um gegen das vorzugehen, was ein Angestellter als „Fehlinformation“ bezeichnete, die von „informationsarmen Wählern“ geteilt wird.

Der Mitbegründer bezieht sich an anderer Stelle im Videoclip auf den internen Thinktank „Jigsaw“ des Unternehmens, das Tools entwickelt hat, um Nutzer von „extremistischen“ Inhalten in den Suchergebnissen sowohl in der Google-Suche als auch auf YouTube abzulenken.

Eine weitere Geschichte

Powerline: It’s Official, Google Is a Democratic Party Front
[Es ist offiziell, Google ist eine Front der Demokratischen Partei]

Powerline:

Alle Redner drücken ihre Trauer über Donald Trumps Wahl aus. Alle Sprecher gehen davon aus, dass jeder Google-Mitarbeiter ein Demokrat ist und erstaunt und entsetzt ist, dass Hillary Clinton – der schlimmste und korrupteste Präsidentschaftskandidat der modernen Geschichte – verloren hat. Es gibt viele Diskussionen darüber, was Google tun kann, um die durch die Brexit- und Trump-Wahlen veranschaulichte weltweite Widrigkeit umzukehren. Die wahnsinnige Doktrin des „weißen Privilegs“ erhebt ihren Kopf.

Hier ist eine andere Geschichte aus dem Powerline Blog

Man muss es gesehen haben, um es zu glauben. Nach dem einstündigen  Stoßzeufzer -OK, um fair zu sein, es gibt auch ein großes Element von Schadenfreude und Sie werden viel davon genießen – wahrscheinlich werden Sie mehrere Reaktionen verspüren:

  1. Diese Leute mögen bestimmte wertvolle technische Fähigkeiten haben, aber sie sind nicht sehr intelligent und zeigen ungewöhnlich wenig Selbsterkenntnis.
  2. Es ist bemerkenswert, dass sie eine solch außergewöhnliche Monokultur in einer Organisation mit Tausenden von Mitarbeitern erreichen können. Es erfordert eine kräftige Durchsetzung des richtigen Denkens.
  3. Es ist leicht zu erkennen, wie diese einheitlich linken Roboter / Menschen nahtlos zum Widerstand gegen die ordnungsgemäß gewählte Trump-Administration umgewandelt wurden.

Das Video:

Also was können Sie tun?

Vermeiden Sie Google. Vermeiden Sie Google Mail und die Suche über Google

Zum Suchen empfehle ich DuckDuckGo und Mojeek . Von den beiden ist Mojeek meiner Meinung nach das bessere Tool, da es keine Google-orientierte Indexierungsbibliothek verwendet.

Update:

Eine E-Mail, die exklusiv von „Tucker Carlson Tonight“ erhalten wurde, zeigt, dass ein leitender Google-Mitarbeiter die Ressourcen des Unternehmens einsetzte, um die Wahlbeteiligung so zu erhöhen, dass Clinton die Wahlen gewinnen könnte.

Gefunden auf WUWT vom 13.09.2018

Übersetzt durch Andreas Demmig

https://wattsupwiththat.com/2018/09/13/google-video-leak-proves-they-are-evil-after-all/

 

Auf Eike fanden Sie dieses Thema u.a. im Oktober 2017, auch von WUWT

https://www.eike-klima-energie.eu/2017/10/07/googles-such-einstellung-gegenueber-konservativen-news-seiten-wurde-quantifiziert/

 

Vorankündigung:

Zu dem oben beklagtem Problem mit den Suchmaschinen, habe ich mir einen kleinen Test überlegt.

  • In Kürze berichte ich Ihnen davon gerne.

Andreas Demmig

 



„Die Stürme nehmen zu, der Klimaerwärmung wegen“ – Unterschiedliche Positionen von Al Gore vs. Wissenschaftler

geschrieben von Andreas Demmig | 21. September 2018

„Dies ist das erste Mal in der Geschichte, dass zwei große Stürme gleichzeitig vom Atlantik und vom Pazifik das Festland erreichen und jeder Beobachter erinnert sich an einige seiner Vorgänger„, sagte Gore am 14.09.2018 beim Global Climate Action Summit in San Francisco.

Ganz falsche Behauptung. Für den Atmosphärenwissenschaftler des Cato-Instituts, Ryan Maue war es ein leichtes, Gore zu widerlegen. Al Gore bezog sich auf den Hurrikan Florence und den Super-Taifun Mangchut.

View image on Twitter

Ryan Maue | weathermodels.com

Al Gore behauptete (in betrügerischer Absicht), dass es keine Beweise dafür gebe, dass wir im Atlantik und im Pazifik jemals Hurrikane gehabt hätten, die zur selben Zeit das Land erreichten. #GCAS2018

Offenbar aus dem verpatzten NBC News Artikel zitiert

NBC News veröffentlichte den Sonntag zuvor ‚… dass wenn zwei Stürme in zwei verschiedenen Ozeanen zur gleichen Zeit brodeln, dieses ein Symptom der vom Menschen verursachten globalen Erwärmung sein könnte. Da es selten ist, zwei große Zyklone wie Hurricane Florence und Super Taifun Mangkhut gleichzeitig zu erleben. ‚

Gore griff das auf und behauptete darüber hinaus: „… dieses ist ein seltenes Ereignis, dass im Atlantik und Pazifik Stürme zur gleichen Zeit anlanden. … gewöhnlich, wenn im Pazifik Stürme toben ist es ruhig im Atlantischen Ozean.“

Ryan Maue twitterte: „Es ist nicht selten, dass Hurricanes gleichzeitig im Atlantik und im Pazifischen Ozean aktiv sind. Das hat auch nichts mit der globalen Erwärmung zu tun.

— View image on Twitter am 14. September 2018

Ryan Maue: Im NBC News Beitrag wird der Punkt über anhaltende Hurrikane und ihre Häufigkeit komplett ausgelassen – ohne irgendeinen Beweis- gleichzeitige Stürme an beiden Küsten sind überhaupt nicht selten. https://www.nbcnews.com/news/us-news/rare-event-atlantic-pacific-churn-storms-same-time-n907826 …

***

In dem verlinkten Beitrag ist auch eine gegenteilige Ansicht gebracht:

… Dennis Feltgen, ein Meteorologe am National Hurricane Center in Miami, ist skeptisch gegenüber dem Argument, dass Stürme in beiden Ozeanen gleichzeitig selten wären.

Er wies darauf hin, dass der Atlantik und der Pazifik die Erwartungen der National Oceanic and Atmospheric Administration NOAA für die Saison erfüllen: durchschnittliche oder unterdurchschnittliche Taifune im Atlantik, mit neun bis 13 benannten Stürmen und nahezu oder überdurchschnittlichen Hurrikane im Pazifik, mit 14 bis 20 benannten Stürmen.

Es ist „überhaupt nicht ungewöhnlich“, schrieb Feltgen per E-Mail.

Hurricane Florence erreichte North Carolina (heute) als Kategorie-1-Sturm. Der Super-Taifun Mangkhut steht kurz vor den Philippinen und erreicht bis zu 250km/ Stunde.

Gefunden auf The Daily Caller vom 14.09.2018

http://dailycaller.com/2018/09/14/al-gore-fraudulent-hurricane-landfalls

***

Ergänzung zum Thema 

Dr. Roy Spencer, ein Meteorologe, erschien in der Sendung „Tucker Carlson Tonight“, um seine Ansichten über Naturkatastrophen zu diskutieren und darüber, ob die globale Erwärmung ihre Häufigkeit beeinflusst oder nicht.

Aufzeichnung:

… „Warum erzählen Medien wie die Washington Post so dumme Sachen? Die Leute, die uns in den Medien über die globale Erwärmung informieren, sind Leute wie Al Gore, Bill Nye, The Science Guy, Neil deGrasse Tyson, Leute, die nichts von atmosphärischer Wissenschaft verstehen. Man muss sich nur die Aufzeichnungen anschauen „, sagte Dr. Spencer.

Spencer war eingeladen, als Reaktion auf die Medien, die Präsident Trump für Hurrikan Florence beschuldigten. In der Washington Post vom Dienstag hieß es: „Ein weiterer Hurrikan ist dabei, unsere Küste zu zerstören. Trump ist der Komplize.“

… „Bill Nye ist der ‘Science Guy’ [~Wissenschafts- Typ]. Die Bezeichnung ist Teil seines Namens. Das heißt aber nicht, dass er viel von Atmosphären Wissenschaft versteht.

Außerdem hat er ein häufig geschautes YouTube-Video Namens „Climate 101“, wo er ein Experiment vorgetäuscht hat „, antwortete Spencer. „Er füllte CO2 in ein Glas und richtete eine grelle Lampe darauf um zu zeigen, dass sich das Glas aufgrund des zusätzlichen CO2 im Inneren aufwärmte. Aber der Fernseh-Meteorologe Anthony Watts zeigte geschickt, dass das Ganze gefälscht war. Es ist lächerlich.“

Gefunden auf The Daily Caller ebenfalls vom 14.09.2018

http://dailycaller.com/2018/09/14/meteorologist-fact-checks-bill-nye-on-whether-climate-change-has-led-to-more-natural-disasters/

Übersetzung und Zusammenstellung Andreas Demmig



Deutsche Studie über Folgen eines längeren Stromausfalls nun auch in Australien verbreitet

geschrieben von Andreas Demmig | 21. September 2018

Auf STT wurde bereits 2016 vom dejau-vu fehlender Energieversorgung berichtet. Ein plötzlicher Einbruch des Windes während eines heftigen Frühlingssturms – die Windräder schalteten bei zu starkem Wind automatisch ab und ließen die Netzversorgung „zusammenbrechen“.

Auch auf Eike konnten Sie darüber hier und hier lesen.

In einigen Teilen der Stadt Adelaide war die Stromversorgung innerhalb von 5 bis 6 Stunden wiederhergestellt, während einige Vororte 24 Stunden oder länger ohne Strom waren. Regionale Zentren wie Port Lincoln, Whyalla und Ceduna waren tagelang ohne Strom, und abgelegenere Städte und ländliche Gebiete waren mehr als eine Woche lang ohne Strom, einige für fast zwei Wochen.

BHP Billitons Gold-, Kupfer- und Uranbergwerk Olympic Dam (das Rückgrat der sich abschwächenden SA-Wirtschaft) hatte vom 28. September bis zum 13. Oktober keine Stromversorgung mehr, was allein dort auf 100 Mio $ Ausfallkosten geschätzt wurde. Nach The Australian verursachte der Stromausfall insgesamt 367 Mio $ an Kosten.

Gehen die Lichter mal für eine Stunde oder so aus, während alle sicher zu Hause sind, könnte das Erlebnis sogar Spaß machen, wenn nicht sogar ein bisschen romantische Anregungen bringen. Kerzen kommen heraus, zusammen mit Karten und Brettspielen; Wer diskutiert nicht auch mal gerne über vergessene Regeln bei Monopoly und ähnlichem? Manche genießen es sogar, dass sie für eine Weile telefonisch nicht erreichbar sind.

Aber wenn diese Einschränkungen Teil des täglichen Lebens werden und / oder die Zeiten ohne Energieversorgung die Arbeit, die Gesundheit und die Sicherheit der Menschen beeinträchtigen, ist der Spaß vorbei. Der Verlust von Mobilfunkdiensten in Notsituationen verschärft das Ganze und schafft mehr unnötige, womöglich tödliche Risiken.

Der Verlust von Straßenbeleuchtung und Ampeln macht die abendliche Pendelfahrt zu einem Spiel von Leben und Tod. Aber das sind nur die offensichtlichsten Konsequenzen eines Stromausfalls in einer Stadt, einem Staat oder einem Land.

Seit einem Jahrzehnt werden die Deutschen mit dem Chaos von Wind- und Solarenergie beschäftigt. Es ist daher nicht verwunderlich, dass sie sich schon einmal Gedanken gemacht haben, was passiert, wenn der Strom ausfällt.

Australier (abgesehen von denen, die in Südaustralien leben) mögen denken, dass die Auswirkungen dessen, was unten beschrieben ist, ziemlich fern sind. Denken Sie jedoch nochmal drüber nach.

New South Wales hat in diesem Jahr bereits drei Beinaheausfälle erlebt. Und wenn die Nachfrage nach Strom im kommenden Sommer steigt, werden New South Wales und Victoria mit erwarteten ernsthaften Kapazitätsengpässen und zu geringer Reserve die gleiche Art von Lastabwurf und Stromausfällen erleiden, die in Südaustralien zur Routine geworden sind.

Sagen Sie nicht, dass wir Sie nicht gewarnt haben. Hier ist Ihr Entwurf für einen Blackout. Wir empfehlen Ihnen, es auszudrucken und es neben den Fackeln und Kerzen bereit zu halten, bereit für Ihre nächste Rückkehr in das finstere Mittelalter.

Erschienen auf stopthesethings  am 12.09.2018

Übersetzt durch Andreas Demmig

https://stopthesethings.com/2018/09/12/blackout-blueprint-german-study-reveals-what-really-happens-when-power-supplies-fail/

***

 

Was passiert bei einem Blackout: Folgen eines anhaltenden und weit reichenden Stromausfalls

Auf STT wird nun die englische Fassung des Berichts übernommen. Für unsere deutschen Leser weiter unten nur die Zusammenfassung. Den kompletten Bericht finden Sie hier:

https://www.tab-beim-bundestag.de/de/pdf/publikationen/berichte/TAB-Arbeitsbericht-ab141.pdf

Meine Recherche brachte mich auch zu den Suchergebnissen auf der Seite des TAB: zu diesem Thema
(Büro für Technologiefolgenabschätzung beim Deutschen Bundestag).

Sicherlich auch mal interessant zum Stöbern.

Im Mai 2011 gab es dazu eine Veranstaltung in Berlin. Vielleicht war einer unserer Leser dort und kann etwas berichten?

 

Zusammenfassung aus o.g.  Bericht.

In modernen, arbeitsteiligen und hochtechnisierten Gesellschaften erfolgt die Versorgung der Bevölkerung mit (lebens)notwendigen Gütern und Dienstleistungen durch ein hochentwickeltes, eng verflochtenes Netzwerk »Kritischer Infrastrukturen«.

Dazu zählen u. a. Informationstechnik und Telekommunikation, Transport und Verkehr, Energieversorgung oder das Gesundheitswesen. Diese sind aufgrund ihrer internen Komplexität sowie der großen Abhängigkeit voneinander hochgradig verletzbar.

Terroristische Anschläge, Naturkatastrophen oder besonders schwere Unglücksfälle haben nicht erst im zurückliegenden Jahrzehnt offenkundig gemacht, welche weitreichenden Folgen die Beeinträchtigung oder der Ausfall Kritischer Infrastrukturen für das gesellschaftliche System insgesamt haben können.

Aufgrund der nahezu vollständigen Durchdringung der Lebens- und Arbeitswelt mit elektrisch betriebenen Geräten würden sich die Folgen eines langandauernden und großflächigen Stromausfalls zu einer Schadenslage von besonderer Qualität summieren.

Betroffen wären alle Kritischen Infrastrukturen, und ein Kollaps der gesamten Gesellschaft wäre kaum zu verhindern. Trotz dieses Gefahren- und Katastrophenpotenzials ist ein diesbezügliches gesellschaftliches Risikobewusstsein nur in Ansätzen vorhanden.

 Mit einem Beschluss des Ausschusses für Bildung, Forschung und Technikfolgenabschätzung wurde das Büro für Technikfolgen-Abschätzung beim Deutschen Bundestag (TAB) beauftragt, die Folgen eines langandauernden und großflächigen Stromausfalls systematisch zu analysieren. Zugleich sollten die Möglichkeiten und Grenzen des nationalen Systems des Katastrophenmanagements zur Bewältigung einer solchen Großschadenslage aufgezeigt werden.

***

Auch auf Eike haben wir Sie dazu bereits informiert

https://www.eike-klima-energie.eu/2016/08/24/energiewende-und-blackout-the-day-after/

 



Die „Milliarden-Dollar-pro-Jahr-Klimaindustrie“ kauft Staatsanwälte

geschrieben von Andreas Demmig | 21. September 2018

Diese Kampagne kumuliert in einer „Strafverfolgungsmitgliedschaft“ (so der Bericht), weil er es politischen Spendern ermöglicht, Staatsanwälte „im Dienste einer ideologischen, linken, klimapolitischen Agenda“ zu bezahlen.

„Damit sollen Interessenten der Geldgeber oder deren Begünstigte durch hohe Staatsanwälte vertreten werden, welche die Polizeigewalt des Staates befehligen, um demokratische Prozesse zu umgehen und Gegner ihrer politischen Agenda kaltzustellen bzw. mundtot zu machen“ schrieb Senior Fellow Chris Horner des Competitive Enterprise in seinem Bericht. Eine Kopie davon wurde dem Daily Caller übergeben.

Horners Auswertung geht tiefer als die ersten Berichte im Daily Caller über die Finanzierung von Rechtsanwälten. Durch eine mit 6 Mio $ ausgestattete Stiftung des ehemaligen New Yorker Bürgermeisters und aktiven Klimaalarmisten Michael Bloomberg, sollen „fortschrittliche saubere Energie, Klimawandel und umweltrechtliche Positionen“ in den Büros der Generalstaatsanwälte voran getrieben werden. „Routinemäßig werden vor der Veröffentlichung von Regulierungen und Gesetzen Rechtsstreitigkeiten erzwungen.“

Horners Bericht beschreibt die Aktionen einer Gruppe von Staatsanwälten und Aktivisten detailliert, angeführt vom ehemaligen New Yorker Generalstaatsanwalt Eric Schneiderman, was schließlich dazu führte, dass der ehemalige New Yorker Bürgermeister Mike Bloomberg für juristische Mitarbeiter bezahlte, um staatliche Strafverfolgungsbehörden zu beeinflussen.

Schneiderman brachte einige Bundesstaaten dazu, den Ölgiganten ExxonMobil zu untersuchen, weil dieser angeblich Investoren und die Öffentlichkeit über die Schwere der vom Menschen verursachten globalen Erwärmung irregeführt habe. Seine breitere Koalition, die „AGs United For Clean Power“ [vereinigte Generalstaatsanwälte für saubere Energie], versprachen zusammen für eine durchgreifendere Klimapolitik zu arbeiten, aber diese Koalition scheint nach ihrer Gründung im Jahr 2016 auseinandergefallen zu sein.

Generalstaatsanwälte von mindestens sechs Bundesstaaten haben fremd-finanzierte juristische Mitarbeiter eingestellt, darunter Maryland, Massachusetts, New York, Oregon, Washington und der District of Columbia.

Gehälter und Leistungen für juristische Stipendiaten werden vom State Energy and Environmental Impact Center (SEEIC) [… unterstützt Staatsanwälte bei der Verteidigung und Förderung von sauberen Energie, Klima- und Umweltgesetzen und -politiken.] an der New York University School of Law bezahlt, was 2017 mit Mitteln von Bloomberg Philanthropien finanziert wurde.

Bloomberg erwägt eine Präsidentskanditatur für die Demokraten, gestützt auf seinen langjährigen Umweltaktivismus. Über „nonprofit Gruppen“ startete Bloomberg Kampagnen, um die USA im Pariser Klimaabkommen zu halten und er finanzierte Klimakampagnen, um grüne Energie zu fördern und Kohlekraftwerke zu schließen.

SEEIC und die Teilnehmerstaaten behaupten, dass der Einsatz von privat finanzierten Anwälten legal ist und keine ethischen Bedenken aufwirft, Horner hat diese Behauptungen jedoch in Frage gestellt.

Gestützt auf Dokumente, die er erhalten hat, beschrieb Horner das Schema „… nutzt Non-Profit-Organisationen als aktive Speerspitze, durch die die Geldgeber gewählte [und geeignete] Mandatsträger unterstützen können, sowie deren Büros zu nutzen, um bestimmte Politiken zu fördern, die von den Gebern bevorzugt werden. … auch werden diese Art von Arrangements verwendet, um politische Gegner – wie z.B. fossile Brennstofffirmen und konservative Gruppen – zu verfolgen.“

Das Büro des New York Generalstaatsanwaltes erklärte ganz offen, dass sie einen privat finanzierten Anwalt brauchen, der daran arbeitet, „Modelle für zwei verschiedene Arten von allgemeinen Rechtsfällen (Common-Law) zu entwickeln, um Schadenersatz von Unternehmen mit fossilen Brennstoffen zu verlangen.

Eine Handvoll Städte und Bezirke haben Dutzende von Unternehmen mit fossilen Brennstoffen wegen angeblicher Schäden durch die vom Menschen verursachte globale Erwärmung verklagt. New York City war eine dieser Städte, aber ihre Klage wurde im Juli abgewiesen.

Horner bemerkte auch, dass die Bundesstaaten, um eine Finanzierung durch SEEIC zu bekommen, „versprechen sollten, dass diese Arbeit ausschließlich im Sinne dieser privaten Finanzierung getan wird“ und versprechen, einen privat finanzierten Anwalt zu engagieren, um „politische Positionen für fortschrittliche saubere Energie, Klimawandel und Umweltgesetzgebung voranzubringen“.

Die Vereinbarung der Bundesstaaten mit SEEIC forderte die Staatsanwälte außerdem auf, sich mit ihnen und „interessierten Verbündeten“ zu koordinieren, bei rechtlichen, regulatorischen und kommunikativen Bemühungen in Bezug auf saubere Energie, Klimawandel und Umweltfragen „.

Erschienen auf The Daily Caller am 29.08.2018

Übersetzt durch Andreas Demmig

https://dailycaller.com/2018/08/29/weaponize-attorney-generals/