Michael Schnell, Hermann Harde
1. Vorbemerkungen
Die Emissionen fossiler Brennstoffe werden für einen Klimanotstand mit katastrophalen Folgen für unseren Planeten verantwortlich gemacht, wenn die weltweiten anthropogenen Emissionen nicht rasch gestoppt werden. Grundlage dieser Vorhersagen ist der atmosphärische Treibhauseffekt (TH-Effekt), der auf Jean-Baptiste Joseph Fourier im Jahr 1824 zurückgeht [1]. Er untersuchte den Energiehaushalt der Erde, um die Oberflächentemperatur zu erklären. Dabei ging er davon aus, dass sich die Atmosphäre ähnlich wie ein Glasfenster verhält, das für die Sonnenstrahlung transparent ist, aber die vom Boden emittierte Infrarotstrahlung (IR) blockiert. Der Wärmeaustausch durch Konvektion oder Wärmeleitung mit der Umgebung wurde in diesem Modell weitgehend vernachlässigt.
Weiter ist festzustellen, dass selbst viele Klimaexperten nicht wirklich zur Kenntnis nehmen, wie sich Treibhausgase (TH-Gase) tatsächlich auf unser Klima auswirken. Dies führt häufig zu dramatischen Fehlinterpretationen in populärwissenschaftlichen Veröffentlichungen, sogar in der Zusammenfassung für politische Entscheidungsträger (6. Sachstandsbericht AR6 des IPCC [2]). Andererseits führen diese Übertreibungen bei Menschen mit klarem Gespür und Verständnis für reale physikalische Sachverhalte zu starken Zweifeln an einem vom Menschen verursachten Klimawandel und der Existenz des Treibhauseffekts, der fast ausschließlich auf theoretischen Überlegungen beruht.
Der Hauptgrund für diese Zweifel ist ein fehlender, nachvollziehbarer Nachweis des TH-Effektes, obwohl es in den letzten 120 Jahren viele Versuche gab, diesen Effekt durch mehr oder weniger einfache Laborexperimente zu bestätigen oder zu widerlegen. Direkte Messungen an der Atmosphäre werden zu stark durch Konvektions-, Turbulenz- oder Streueffekte beeinflusst, um den relativ geringen Beitrag von Treibhausgasmolekülen zu einer lokalen Erwärmung der Luft oder der Erdoberfläche zu quantifizieren, dies bei lokalen Tag-Nacht-Schwankungen bis zu 60 °C und durch saisonale Zyklen sogar bis zu 100 °C.
1.1 Historische Anmerkungen
Eine der wesentlichen experimentellen Untersuchungen geht auf R. W. Wood (1909) [3] zurück, der zwei Kästen mit normaler Luft verwendete. Eine Box war mit einem Glasfenster abgedeckt, das für Sonnenlicht transparent war, aber IR-Strahlung blockierte, die andere war mit einem NaCl-Fenster abgedeckt, das ebenfalls für IR-Licht transparent war. Seine Messungen zeigten eine deutliche Erwärmung des Innenraums, jedoch keinen oder nur einen vernachlässigbaren Temperaturunterschied zwischen den Boxen.
Daraus schlossen Wood und andere Autoren bei der Wiederholung dieses Experiments (z. B. Allmendinger 2006 [4], Nahle 2011 [5]), dass Infrarotstrahlung, die durch das NaCl-Fenster entweichen kann, nicht oder nur vernachlässigbar zur Erwärmung beiträgt, während der beobachtete Temperaturanstieg in beiden Boxen – anders als Fouriers Interpretation – ausschließlich durch einen unterdrückten konvektiven Wärmeaustausch mit der Umgebung erklärt wird und nicht mit irgendeiner Form von eingeschlossener Strahlung zusammenhängt.
Aber Experimente, die nicht nur eine einzige Temperatur für jede Box messen, sondern die Temperatur am Boden und der Oberseite des Innenraums aufzeichnen, finden bei der Box mit NaCl-Fenster einen um 5°C größeren Temperaturabfall vom Boden bis zur Decke als bei der Glasbox. Die Temperatur am Boden ist dagegen bei beiden Boxen nahezu identisch (V. R. Pratt 2020 [6]). Diese Ergebnisse werden grundsätzlich mit einem etwas anderen Aufbau bestätigt, der eine interne elektrische Heizung anstelle externer Lichtquellen verwendet (E. Loock 2008 [7]). Eine solche Erwärmung vermeidet Unterschiede in der einfallenden Strahlung, die sonst Fenster aus unterschiedlichen Materialien mit unterschiedlichen Verlusten passieren muss. Für den Glaskasten konnte eine höhere Temperatur von 2,5 – 3°C gefunden werden, und beim Austausch des Glases durch eine polierte Aluminiumfolie steigt die Temperatur sogar um weitere ≈ 3°C.
Während die Wood’schen Experimente die Frage beantworten können, ob und inwieweit eine verringerte IR-Transmission zur Erwärmung eines Behälters, oder entsprechend der Troposphäre, beitragen kann, geben sie keine Auskunft über die Wechselwirkung von Treibhausgasen mit IR-Strahlung. Es blieb also weiterhin die Frage, inwieweit solche Gase die IR-Strahlung zumindest teilweise zurückhalten können und inwieweit die einfache Absorption durch TH-Gase oder die umstrittene Rückstrahlung zu einer zusätzlichen Erwärmung des Bodens beitragen könnten. Für solche Untersuchungen ist es erforderlich, einen Behälter mit dem zu untersuchenden Gas zu füllen und dieses mit einer Referenzmessung mit Luft oder einem Edelgas zu vergleichen.
Mittlerweile wurden unterschiedliche Ansätze verfolgt, teils mit äußerer Bestrahlung oder mit innerer Erwärmung (siehe z. B. Loock [7]), teils mit Messung der Gastemperatur oder der IR-Strahlung in Vorwärts- und Rückwärtsrichtung (Seim & Olsen 2020 [8]). Aber entweder konnte keine Erwärmung festgestellt werden oder der beobachtete Temperaturanstieg konnte bei näherer Betrachtung nicht auf einen IR-Strahlungseffekt zurückgeführt werden.
Leider wurden im Internet einige fehlerhafte Demonstrationen mit angeblichen Temperaturunterschieden von mehr als 10°C präsentiert, die die starke Wirkung der Treibhausgase beweisen sollten (siehe z. B. Ditfurth 1978 [9]). Bei näherer Betrachtung zeigt sich jedoch, dass die höhere Temperatur hauptsächlich durch einen Schichtungseffekt, verbunden mit einer erhöhten Isolation, verursacht wird, wenn schwereres CO2 von unten in ein Gefäß eingefüllt wird (Schnell 2020 [10]). Bei diesen angeblichen Demonstrationen des Treibhauseffektes wird übersehen, dass reines CO2 trotz Erwärmung eine höhere Dichte als die darüber befindliche Luft hat und dadurch keinen thermischen Auftrieb verursacht. Ohne anschließende Homogenisierung führt dies zu einem erhöhten Temperaturanstieg in der CO2-Schicht. Solche Experimente zeigen lediglich, dass CO2 IR-Strahlung absorbieren kann, was eigentlich nicht überraschen sollte.
Und wirklich problematisch ist es, wenn einer der Preisträger des Friedensnobelpreises 2007 eine Web-basierte Kampagne mit mehreren Werbespots im Fernsehen initiiert, die darauf abzielt, das Bewusstsein für eine Klimakrise zu schärfen. Als „Beweis“ wird ein völlig unrealistisches und nicht reproduzierbares Video-Experiment des TH-Effekts präsentiert (Al Gore’s Climate 101 Video Experiment 2001 [11]), das mittlerweile durch mehrere Überprüfungen als fehlerhaft entlarvt wurde (Watts 2011 [12], Solheim 2016 [13]).
Solche Experimente werden leider weiter genutzt, um weltweit Angst zu verbreiten und unsere Gesellschaft mit der Botschaft zu indoktrinieren, dass wir unsere Erde nur retten können, indem wir künftig alle Treibhausgasemissionen stoppen. Solche Experimente untergraben alle ernsthaften Versuche, den erwarteten Einfluss von Treibhausgasen auf unser Klima zu diskutieren und zu analysieren. Politische Vorstellungen, Spekulationen oder religiöser Glaube sind keine ernsthaften Berater, um eine erfolgreiche Zukunft zu sichern. Unser Wissen und unser technischer Fortschritt basieren auf seriösen wissenschaftlichen Grundlagen.
1.2 Ziel der Untersuchungen
Es ist höchste Zeit, die endlosen Spekulationen über die katastrophalen Auswirkungen oder die Nichtexistenz eines atmosphärischen TH-Effektes zu beenden und sich auf verlässliche Untersuchungen zu konzentrieren, die es ermöglichen, die Größe und den begrenzenden Einfluss von Treibhausgasen durch anthropogene Emissionen fossiler Brennstoffe auf die globale Erwärmung zu quantifizieren. In einer aktuellen Arbeit (Harde & Schnell 2022 [14]) wird der theoretische Hintergrund des TH-Effektes zusammengefasst, und es werden erstmals quantitative Messungen für die Treibhausgase CO2, CH4 und N2O unter ähnlichen Bedingungen wie in der unteren Troposphäre vorgestellt. Eine gekürzte, weniger technische Version steht als PDF zur Verfügung [15] und wird in komprimierter Form im zweiten Teil dieses Artikels wiedergegeben.
Um den Strahlungsaustausch zwischen Körpern unterschiedlicher Temperatur aufzuzeigen und die Besonderheiten des TH-Effektes hervorzuheben, wurden detaillierte Modell-Untersuchungen durchgeführt, bei denen die TH-Gase durch eine geschwärzte Metallplatte in einem Strahlungskanal ersetzt werden (Schnell & Harde 2023 [16]). Als Einführung in das grundlegende Prinzip des atmosphärischen TH-Effektes werden im ersten Teil dieses Artikels zunächst diese Untersuchungen vorgestellt, bevor im zweiten Teil auf die TH-Gase eingegangen wird.
2. Demo-Experiment mit Metallplatte
2.1 Der Strahlungskanal
Der Versuchsaufbau zur Demonstration des Strahlungsaustausches und des TH-Effekts besteht aus einem vertikalen Hohlzylinder aus Styropor. Er ist als modularer Aufbau konzipiert und kann daher leicht für verschiedene Experimente umgebaut werden (Abb. 1, Details siehe: Schnell & Harde 2023 [16]).
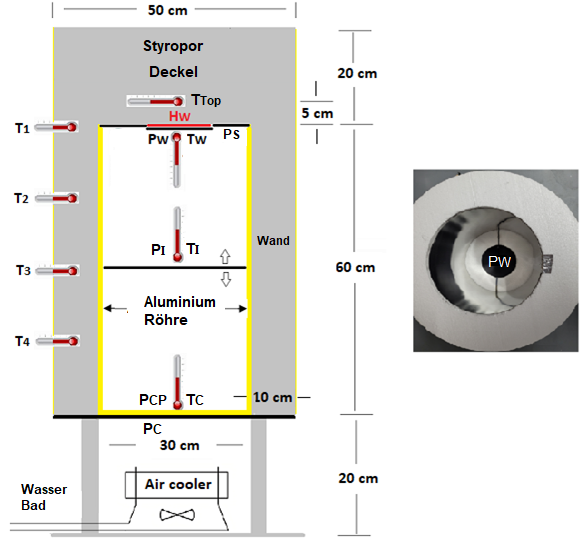
Abb. 1: Schematischer Versuchsaufbau. Die Indizes stehen für: W = warm, C = cold, CP = cold polished und I = Intermediate.
Im Styropor-Behälter befinden sich zwei parallele Metallplatten PW und PC im Abstand von 60 cm und zur Simulation des TH-Effektes eine Zwischenplatte PI. Die obere Platte PW ist geschwärzt und kann durch eine elektrische Heizung der Leistung HW beheizt werden. Die untere Platte PC ist ebenfalls geschwärzt und wird durch einen Luftkühler in ihrer Temperatur stabilisiert. Sie ist CPC kälter als die Raumtemperatur TRaum. Für ein Kontrollexperiment kann diese untere Platte durch eine polierte PCP-Scheibe mit sehr geringem Absorptionsvermögen und damit geringem Emissionsvermögen ersetzt werden, um die Intensität der Gegenstrahlung durch Reflektion zu erhöhen.
Die Innenseite des Styroporbehälters (als Strahlungskanal bezeichnet) kann mit einem Aluminiumrohr oder einer dünnen Al-Folie ausgekleidet werden, wodurch IR-Strahlung durch Mehrfachreflexion und Streuung effizient von einer Platte zur anderen geleitet wird. Dies ermöglicht einen intensiven Strahlungsaustausch zwischen den Platten, und trotz teilweise leichter Absorptionsverluste an der Innenwand werden ohne Zwischenplatte im Kanal mehr als 70 % der zugeführten Heizleistung HW durch IR-Strahlung abgeführt.
Ein kleinerer Teil der über die Platte PW zugeführten Heizleistung HW fließt durch einen mechanischen Wärmefluss über die Styroporisolierung nach außen ab (siehe hierzu Tabelle 2).
Temperatur-Sensoren rund um den Strahlungskanal detektieren diese Wärmeströme.
Durch die senkrechte Anordnung des Strahlungskanals stellt sich eine stabile Luft-Schichtung (oben warm, unten kalt) ein, die Konvektion als Wärmetransport ausschließt.
Die wichtigsten Informationen für die Untersuchungen liefern aber die Temperatur TW und die Heizleistung HW der warmen Platte PW. Diese Platte fungiert gleichzeitig als Wärmequelle und Sensor.
2.2 Gegenstrahlung
Ziemlich kontrovers diskutiert wird die These, dass ein erhitzter Körper durch die Strahlung eines kälteren Körpers oder Gases weiter erwärmt werden kann. Dies wird als Verletzung des zweiten Hauptsatzes der Thermodynamik angesehen, obwohl Clausius als einer der Väter dieses Gesetzes einen gegenseitigen Wärmeaustausch durch Strahlung nie in Frage gestellt hat.
Während die IR-Emission der beheizten Platte PW eindeutig durch ihre Temperatur TW und den Emissionsgrad εW ≈ 1 der Platte definiert wird, ist die Strahlung aus der Umgebung, die sogenannte Rückstrahlung, naturgemäß deutlich komplexer. Diese Strahlung resultiert aus einer Überlagerung von Emissionen, Reflexionen und Strahlungsverlusten, die von der gekühlten Platte und der Kanalwand des Hohlzylinders verursacht werden. Die Auswirkung der Rückstrahlung kann durch Variation der Oberfläche und der Temperatur der Grundplatte demonstriert werden. Für diese Messungen wird die Zwischenplatte PI entfernt und das Aluminiumrohr im Strahlungskanal verwendet
Die folgenden Untersuchungen verdeutlichen, wie die Temperatur der konstant beheizten Platte PW durch die Rückstrahlung beeinflusst wird.
a) Grundplatte PC auf beiden Seiten schwarz beschichtet:
Die ersten 100 Minuten zeigen ein thermisches Gleichgewicht, wobei Platte PW eine Temperatur TW = 24,0 °C erreicht. Die schwarz beschichtete PC-Grundplatte wird dann langsam von den vorherigen 17 °C auf 11 °C abgekühlt (Abb. 2a, blaue Linie), wodurch ihre IR-Emission SC nach dem Stefan-Boltzmann-Gesetz abnimmt. Für die PW-Platte vergrößert sich dadurch der Strahlungsaustausch als Differenz aus abgegebener (SW) und empfangener Leistung (SC):
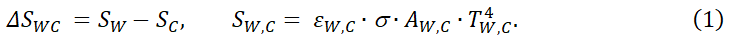
Dabei ist σ die Stefan-Boltzmann-Konstante mit σ = 5.67⋅10-8 W/m2/K4 und AW,C die Fläche der warmen bzw. kalten Platte. Wegen der stärkeren Wärmeabfuhr muss die Temperatur TW entsprechend sinken, wodurch abgeführte und zugeführte Leistung wieder gleich groß werden (Abb. 2a).
Der Strahlungsaustausch, die Strahlungsbilanz zweier unabhängiger Strahler nach Gl. (1), wurde erstmals von Josef Stefan (1879) [17] formuliert und kann mit diesem Experiment auf einfache Weise gezeigt werden.
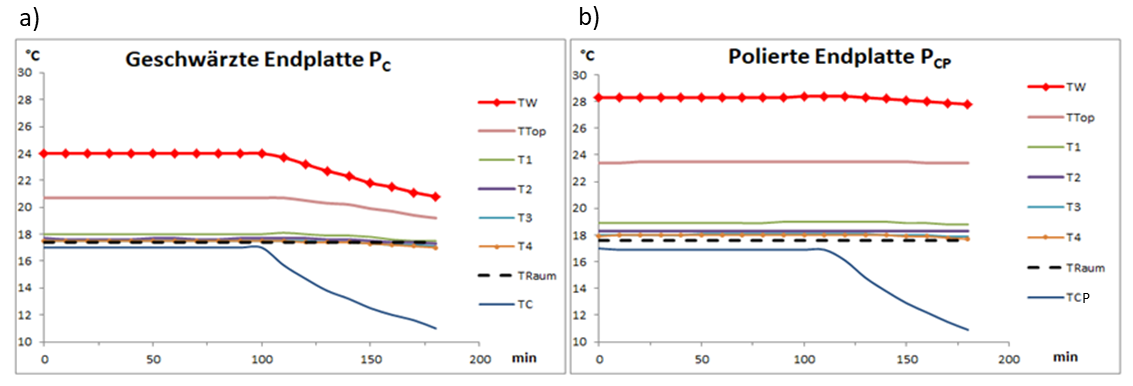
Abb. 2: Auswirkung der Gegenstrahlung auf die Temperatur TW der beheizten Platte PW, a) durch eine geschwärzte Grundplatte PC, b) durch eine polierte Platte PCP.
b) Grundplatte PCP außen geschwärzt und innen auf Hochglanz poliert:
Im thermisches Gleichgewicht wird unter ansonsten gleichen Bedingungen eine 4,9 °C höhere Temperatur TW = 28,9 °C erreicht. Ursache ist der deutlich verringerte Absorptionsgrad αCP der polierten Platte, der eine Zunahme des Reflexionsgrades entsprechend rCP = 1 – αCP bedingt. Anstelle der IR-Emission der Platte PCP wird die Rückstrahlung SC jetzt weitgehend durch die reflektierte, intensivere Strahlung der warmen Platte erzeugt, was nach Gleichung (1) eine geringere Wärmeabfuhr und damit eine höhere TW-Temperatur bedeutet (Abb. 2b).
Im Gegensatz zur geschwärzten Platte zeigt sich beim Abkühlen der PCP-Platte kaum eine Rückwirkung auf die Temperatur TW der oberen Platte. Dies lässt sich durch den geringeren Emissionsgrad εCP ≈ αCP der polierten Platte und die Temperaturunabhängigkeit der Reflexion an der Platte PCP erklären.
Für den Fall von reflektierenden Oberflächen und einer geringen Strahlungsbilanz hat Stefan den Strahlungsaustauschgrad E < εW, εC << 1 eingeführt, der mit dem Experiment b) demonstriert werden kann.
Um es noch einmal zu betonen: Die Grundplatten sind 60 cm von der geheizten Platte PW entfernt und eine Variation ihrer Oberflächengestaltung reicht aus, um starke Temperaturunterschiede der Platte PW zu bewirken, die nur durch Veränderungen der IR-Rückstrahlung erklärbar sind. Eine Veränderung der Wärmeleitung als mögliche Ursache für diese Effekte kann bei diesen Experimenten ausgeschlossen werden, da der grundlegende Versuchsaufbau bei diesen Experimenten nicht verändert wurde und die Temperaturen des Strahlungskanals T1 bis T4 annähernd konstant blieben.
2.3 Quantifizierung der Wärmeströme
Die der PW-Platte zugeführte Heizleistung HW wird sowohl durch IR-Strahlung als auch durch einen mechanischen Wärmestrom JQ abgeführt. Da im thermischen Gleichgewicht nur so viel Wärme abfließen kann, wie durch die Heizung zugeführt wird, addieren sich Strahlungstransport ΔSWC und Wärmeleitung JQ zur Heizleistung HW

Das Verhältnis der beiden Wärmeströme lässt sich bestimmen, wenn eine der beiden Größen ermittelt werden kann, da die andere Größe dann die Differenz zu HW ist.
Der mechanische Wärmestrom JQ ergibt sich nach Fourier in guter Näherung aus der Wärmeleitfähigkeit λS der Styroporisolierung, ihrer Dicke d und Oberfläche AS sowie der Temperaturdifferenz ΔT zur Umgebung:

Dieser Ansatz ist jedoch nicht hilfreich, da unterschiedliche Temperaturen, Dicken und Oberflächen der Styroporisolierung der Versuchsapparatur berücksichtigt werden müssten.
Der Wärmestrom JQ kann jedoch direkt gemessen werden, indem der Strahlungskanal vollständig mit zwölf 5 cm dicken Styroporscheiben gefüllt wird. Es entsteht ein Styroporblock (ohne Strahlungskanal) mit den gleichen Außenabmessungen und den zwei Platten. In diesem Fall kann die zugeführte Wärme HW nur durch den mechanischen Wärmestrom JQ abgeführt werden, wodurch Gl. (2) übergeht in:

Die Berechnungsgrundlage für die Bewertung der Wärmeströme ist der Temperaturanstieg ΔTW, die Temperaturdifferenz vor und nach dem Einschalten der Heizung HW. Mit der Kenntnis von HW und ΔTW kann der Wärmewiderstand ϑ (auch als thermischer Widerstand bezeichnet) der Versuchsapparatur, als Verhältnis von ΔTW zu HW, bestimmt werden als (Einheit °C/W):

Da sich die Beschichtung des Strahlungskanals auf den mechanischen Wärmestrom JQ auswirkt, ergeben sich auch verschiedene Wärmewiderstände, die zur besseren Unterscheidung zur Strahlung hier als Leitungswiderstände ϑJ bezeichnet werden. Dabei zeigt sich, dass eine Beschichtung mit einer Aluminium-Folie eine optimale Lösung darstellt, die die Reflektion im Strahlungskanal verbessert, aber den Leitungswiderstand im Vergleich zum reinen Styropor (ohne Beschichtung) nur unwesentlich verringert (Tabelle 1).
Tabelle 1: Ermittlung der Leitungswiderstände ϑJ in einem Styroporblock
Beschichtung des
Strahlungskanals |
HW
W |
TW
°C |
ΔTW
°C |
J
°C/W |
| ohne |
1,16 |
41,6 |
24,2 |
21,0 |
| Aluminium-Folie |
1,15 |
40,5 |
22,9 |
20,0 |
| Aluminium -Rohr |
1,16 |
38,0 |
20,5 |
17,7 |
Durch schrittweises Entfernen der inneren Styroporscheiben zeigt sich, dass der mechanische Wärmestrom hauptsächlich über den oberen Styropordeckel und die obere Wandisolierung nach außen abfließen, während die Füllung des Strahlungskanals mit Styropor eine vernachlässigbare Veränderung bewirkt. Dadurch lässt sich der Leitungswiderstand des Styroporblocks auch auf den Strahlungskanal übertragen (siehe: Schnell & Harde 2023 [16]). Außerdem hat ruhende Luft eine geringere Wärmeleitfähigkeit als Styropor, und schon aus diesem Grund kann die Wärmeleitfähigkeit des Strahlungskanals nicht größer sein als die des Styroporblocks.
So ergibt sich für den Strahlungskanal mit Aluminium-Folie mit ϑJ = 20,0 °C/W, HW = 1,2 W und ΔTW = 6,5 °C entsprechend Gl. (4) und (5) ein mechanischer Wärmeverluststrom von

Damit wird die durch IR-Strahlung abgeführte Leistung entsprechend Gl. (2) ΔSWC = 0,87 W und stellt mit 73 % den klar dominanten Anteil an der Wärmeabfuhr dar. Das Aluminium-Rohr hat aufgrund seiner glatten, polierten Oberfläche den höchsten Reflexionsgrad, verliert aber zu viel Wärme durch Wärmeleitung und steht daher nur an zweiter Stelle (Tabelle 2).
Tabelle 2: Anteil der Wärme HW, die durch IR-Strahlung abgeführt wird.
Beschichtung des
Strahlungskanals |
HW
W |
ΔTW
°C |
J
°C/W |
JQ
W |
ΔSWC
W |
ΔSWC
% |
| ohne |
1,20 |
8,2 |
21,0 |
0,39 |
0,81 |
67,4 |
| Alu-Rohr |
1,20 |
6,5 |
17,7 |
0,37 |
0,83 |
69,3 |
| Alu-Folie |
1,20 |
6,5 |
20,0 |
0,33 |
0,87 |
72,9 |
2.4 Einfluss paralleler Wärmeströme auf den Treibhauseffekt
Wird die Wärme durch zwei parallele Wärmeströme abgeführt, addieren sich die Wärmewiderstände wie die parallelgeschalteten Widerstände in einer elektrischen Schaltung (Abb. 3):

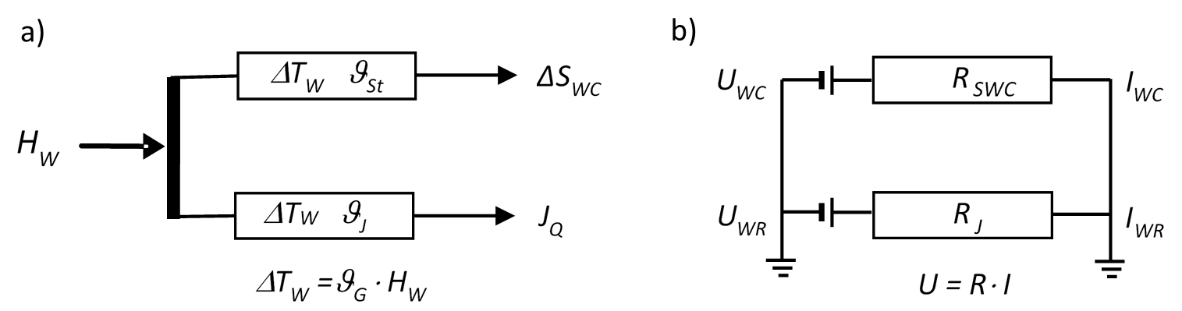
Abb. 3: a) Wärmeflüsse durch Strahlung und Wärmeleitung, b) elektrisches Ersatzschaltbild.
Der Gesamt-Wärmewiderstand ϑG ist damit immer kleiner als jeder Teilwiderstand, was durch einen Vergleich der Wärmebilanzen eines Styroporblocks und eines Strahlungskanals (in beiden Fällen ohne Beschichtung) gezeigt werden kann (Abb. 4).
Im Falle des Styroporblocks (Fall a) ist die Wärmeleitung JQ der einzige Wärmefluss. Die Temperatur der warmen Platte PW erhöht sich um ΔTW = 24,2 °C, was einem Leitungswiderstand ϑJ = 21 °C/W entspricht und gleichzeitig den Gesamt-Wärmewiderstand ϑG darstellt.
Im Falle des Strahlungskanals (Fall b ohne Styroporscheiben) wird die Wärme der Platte PW parallel durch Wärmeleitung und Strahlungsaustausch abgeführt, wodurch sich die Temperatur nur um ΔTW = 8,8 °C erhöht, was den Gesamt-Wärmewiderstand auf ϑG = 7,3 °C/W verringert. Da, wie oben dargelegt, die inneren Styroporscheiben praktisch keinen Einfluss auf den Leitungswiderstand haben, errechnet sich mit ϑJ = 21 °C/W und ϑG = 7,3 °C/W ein Strahlungswiderstand ϑSt = 11,1 °C/W nach Gl. (7).
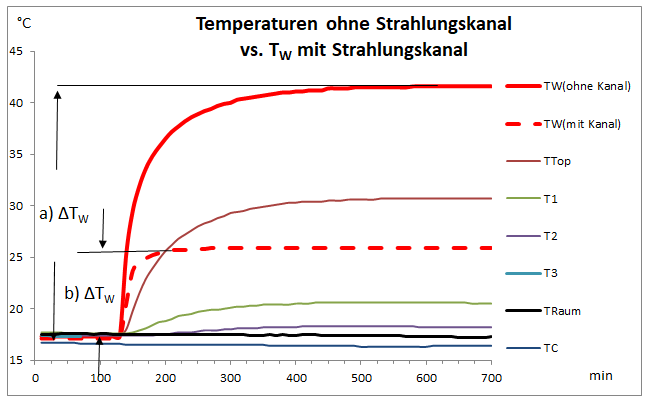
Abb. 4: a) Temperatur TW ohne Strahlungskanal, b) zum Vergleich Temperatur TW mit Strahlungskanal.
Dieser Vergleich zeigt das große Potenzial der IR-Strahlung zur Energieübertragung, wodurch wesentlich mehr Wärme abgeführt wird als durch reine Wärmeleitung.
Die Erdoberfläche, die zu mehr als 70 % aus Wasser besteht, wird i. W. durch drei parallele Wärmeströme, Konvektion, Evapotranspiration und Strahlungsaustausch, gekühlt. Durch den Anstieg der CO2-Konzentration steigt der Strahlungswiderstand ϑSt, wodurch sich die Erdoberfläche leicht erwärmt. Eine Erderwärmung verursacht aber auch eine Zunahme der Wasserverdampfung mit dem Wärmewiderstand ϑEva, wodurch die Erdoberfläche eine zusätzliche Kühlung erfährt und nach Gl. (7) der Wärmewiderstand ϑG wieder sinkt.
Ein solcher Mechanismus ist eine negative Temperatur-Rückkopplung (siehe Harde 2017 [18]), die leider vom IPCC und den dort referierten Klimamodellen nicht berücksichtigt wird und dadurch zu deutlich höheren Prognosen für eine durch CO2 verursachte Erwärmung führt.
Die durch Verdunstung abgeführte Wärme und die daraus resultierende Wolkenbildung erklären, warum Ozeane auch in den Tropen nur eine maximale Oberflächen-Temperatur von rund 32 °C erreichen. Im Gegensatz dazu werden in den Wüsten der Subtropen, die sich nicht durch Wasserverdampfung kühlen können, Rekordtemperaturen erreicht, wie z.B. im Death Valley mit 56,7 °C in zwei Meter Höhe [19] oder sogar Boden-Temperaturen von 94 °C im Furnace Creek bzw. 78,2 °C in der Dascht-e Lut-Wüste. [20].
2.5 Simulation des Treibhauseffekts
Wird eine geschwärzte, dünne Al-Platte als Zwischenscheibe PI in den Strahlungskanal eingebracht, unterbricht diese den Strahlungsaustausch durch einen Absorptions-Emissions-Zyklus, wobei die der Platte zugeführte Energie beidseitig durch Infrarotstrahlung wieder abgegeben wird. Dieser Vorgang entspricht im Prinzip der Wirkung von Treibhausgasen in der Atmosphäre, mit dem Unterschied, dass in der schwarzen Scheibe alle verfügbaren Wellenlängen eines Planck-Strahlers von der Absorptions-Emissions-Unterbrechung betroffen sind. In diesem Modellversuch ist die gekühlte Platte PC die Energiesenke, der Ort, an dem die durch IR-Strahlung übertragene Nettoenergie abgeführt wird.
Der Modellversuch kann auch als Simulation des Einflusses von Wolken auf den Strahlungsaustausch angesehen werden. In diesem Sinne simuliert die Scheibe PI eine vollständige Wolkenbedeckung und PW die Erdoberfläche. Ein weiterer Sensor auf der Scheibe PI liefert Informationen über die an diesem Ort auftretende Temperatur TI, die der Temperatur der Gase bzw. Wolken entsprechen würde.
Definitionsgemäß ist das Maß für den Treibhauseffekt die Temperaturerhöhung ΔTG der warmen Platte im Vergleich zu einer Messung ohne die Platte PI bei sonst gleicher Heizleistung HW. In drei Versuchen, die sich lediglich im Abstand zwischen der Scheibe PI und der warmen Platte unterscheiden, führt die Existenz dieser Platte im Strahlungskanal zu gut beobachtbaren Temperaturunterschieden von bis zu 2,0 °C (Abb. 5, Tab. 3).
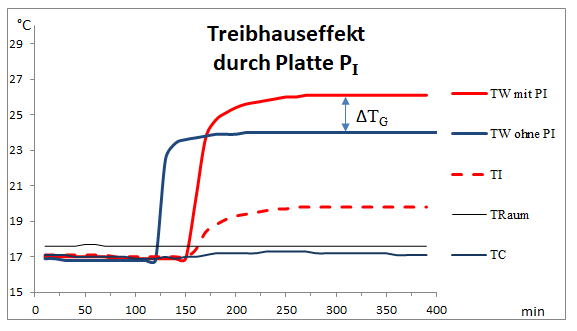
Abb. 5: Temperaturverlauf von TW (Rot) und TI (Gestrichelt) mit Zwischenscheibe PI (5 cm Abstand zu Platte PW). Zum Vergleich die Temperatur TW ohne Scheibe PI (Blau).
Für die Platte PW ist jetzt die Quelle der Rückstrahlung nicht mehr die Platte PC, sondern die wärmere Platte PI mit der Temperatur TI (Rot gestrichelt). Dies führt zu einem Anstieg der Temperatur TW (Rot). Zum Vergleich ist die Temperatur TW ohne die Scheibe PI dargestellt (Blau).
Tabelle 3: Treibhauseffekt einer Aluminiumscheibe
Aluminiumscheibe PI
Abstand zu PW (cm) |
HW
W |
TC
°C |
TW
°C |
TI
°C |
ΔTW
°C |
ΔTG
°C |
G
°C/W |
| 5 |
1,20 |
17,1 |
26,1 |
19,8 |
9,2 |
2,00 |
7,7 |
| 30 |
1,20 |
16,9 |
25,7 |
19,0 |
8,8 |
1,60 |
7,3 |
| 55 |
1,20 |
16,9 |
25,3 |
18,5 |
8,4 |
1,20 |
7,0 |
| ohne Scheibe |
1,20 |
16,8 |
24,0 |
– |
7,2 |
0,00 |
6,0 |
Damit wird erneut bestätigt: Die Temperatur eines beheizten Körpers hängt eindeutig von der Intensität der Gegenstrahlung seiner Umgebung ab, auch wenn diese kälter ist.
Übertragen auf die Atmosphäre lässt sich hieraus ableiten, dass der Treibhauseffekt durch TH-Gase vor allem bei klarem Himmel in Erscheinung tritt. Niedrige Wolken mit ihren vergleichsweise hohen Temperaturen erzeugen dagegen eine so starke Gegenstrahlung, dass die Beiträge durch die Treibhausgase überdeckt und deutlich abgeschwächt erscheinen.
Referenzen
- J. B. Fourier, 1824: Remarques Générales Sur Les Températures Du Globe Terrestre Et Des Espaces Planétaires. In: Annales de Chimie et de Physique, Vol. 27, 1824, S. 136–167, https://books.google.co.uk/books?id=1Jg5AAAAcAAJ&pg=PA136&hl=pt-BR&source=gbs_selected_pages#v=onepage&q&f=false
- IPCC, 2021: Summary for Policymakers. In: Climate Change 2021: The Physical Science Basis. Contribu-tion of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change [Masson-Delmotte, V., P. Zhai, A. Pirani et al. (eds.)]. Cambridge University Press, pp. 3−32, doi:10.1017/9781009157896.001.
- R. W. Wood, 1909: Note on the Theory of the Greenhouse, London, Edinborough and Dublin Philosophical Magazine, Vol. 17, pp. 319-320. https://zenodo.org/record/1430650#.Yoo9kPTP1EY
- T. Allmendinger, 2006: The thermal behaviour of gases under the influence of infrared-radiation, Int. J. Phys. Sci. 11: 183-205. https://academicjournals.org/journal/IJPS/article-full-text-pdf/E00ABBF60017
- N. S. Nahle, 2011: Repeatability of Professor Robert W. Wood’s 1909 experiment on the Theory of the Greenhouse, Biology Cabinet Online-Academic Resources and Principia Scientific International, Monterrey, N. L. https://principia-scientific.org/publications/Experiment_on_Greenhouse_Effect.pdf
- V. R. Pratt, 2020: Wood’s 1909 greenhouse experiment, performed more carefully,
http://clim.stanford.edu/WoodExpt/
- E. Loock, 2008: Der Treibhauseffekt – Messungen an einem Wood’schen Treibhaus, https://docplayer.org/30841290-Der-treibhauseffekt-messungen-an-einem-wood-schen-treibhaus-von-ehrenfried-loock-version.html
- T. O. Seim, B. T. Olsen, 2020: The Influence of IR Absorption and Backscatter Radiation from CO2 on Air Temperature during Heating in a Simulated Earth/Atmosphere Experiment, Atmospheric and Climate Sciences, 10, pp. 168-185, https://doi.org/10.4236/acs.2020.102009.
- H. v. Ditfurth, 1978: Studio-Demonstration in Deutschem TV, ZDF TV-Series „Querschnitte“.
- M. Schnell, 2020: Die falschen Klimaexperimente,
https://www.eike-klima-energie.eu/2020/11/06/die-falschen-klima-experimente/
- A. Gore, D. Guggenheim, 2006: An Inconvenient Truth, Movie, https://www.imdb.com/title/tt0497116/
- A. Watts, 2011: Replicating Al Gore’s Climate 101 video experiment shows that his „high school physics“ could never work as advertised,
https://wattsupwiththat.com/2011/10/18/replicating-al-gores-climate-101-video-experiment-shows-that-his-high-school-physics-could-never-work-as-advertised/?cn-reloaded=1
- J.-E. Solheim, 2016: Start des zweitägigen „Al Gore-Experiments“, 10. Internationale Klima- und Energie-Konferenz (10. IKEK), EIKE, Berlin, https://www.eike-klima-energie.eu/2017/02/04/10-ikek-prof-em-jan-erik-solheim-start-des-zweitaegigen-al-gore-experiments/.
- H. Harde, M. Schnell, 2022: Verification of the Greenhouse Effect in the Laboratory, Science of Climate Change, Vol. 2.1, pp. 1-33, https://doi.org/10.53234/scc202203/10.
- H. Harde, M. Schnell, 2022: Nachweis des Treibhauseffekts im Labor,
http://hharde.de/index_htm_files/Harde-Schnell-THE-m.pdf
- M. Schnell, H. Harde, 2023: Model-Experiment of the Greenhouse Effect, Science of Climate Change, Vol. 3.5, pp. 445 – 462, https://doi.org/10.53234/scc202310/27
- J. Stefan, 1879: Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der kaiserlichen Akademie der Wissenschaften, 79, S. 391 – 428
- H. Harde, 2017: Radiation Transfer Calculations and Assessment of Global Warming by CO2, International Journal of Atmospheric Sciences, Volume 2017, Article ID 9251034, pp. 1-30, https://doi.org/10.1155/2017/9251034.
- Wikipedia, Temperaturextrema, https://de.wikipedia.org/wiki/Temperaturextrema
- Wikipedia, https://en.wikipedia.org/wiki/Dasht-e_Lut
Wegen der nicht genauen Darstellung von Indizes und Sonderzeichen, hier nochmal der Teil 1 als pdfGibt es einen Atmosphärischen Treibhauseffekt Teil 1 Vollständig
 .Bild 1
.Bild 1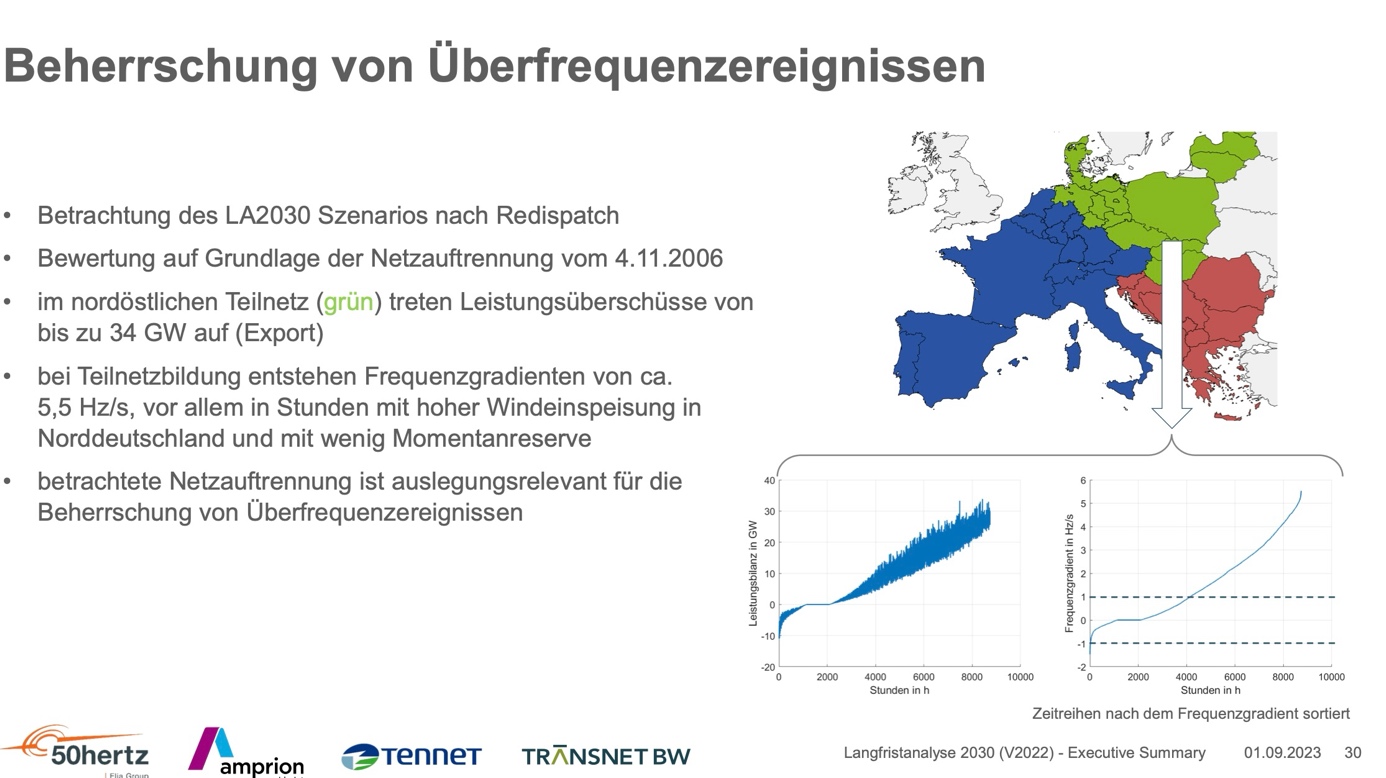 Bild 2
Bild 2








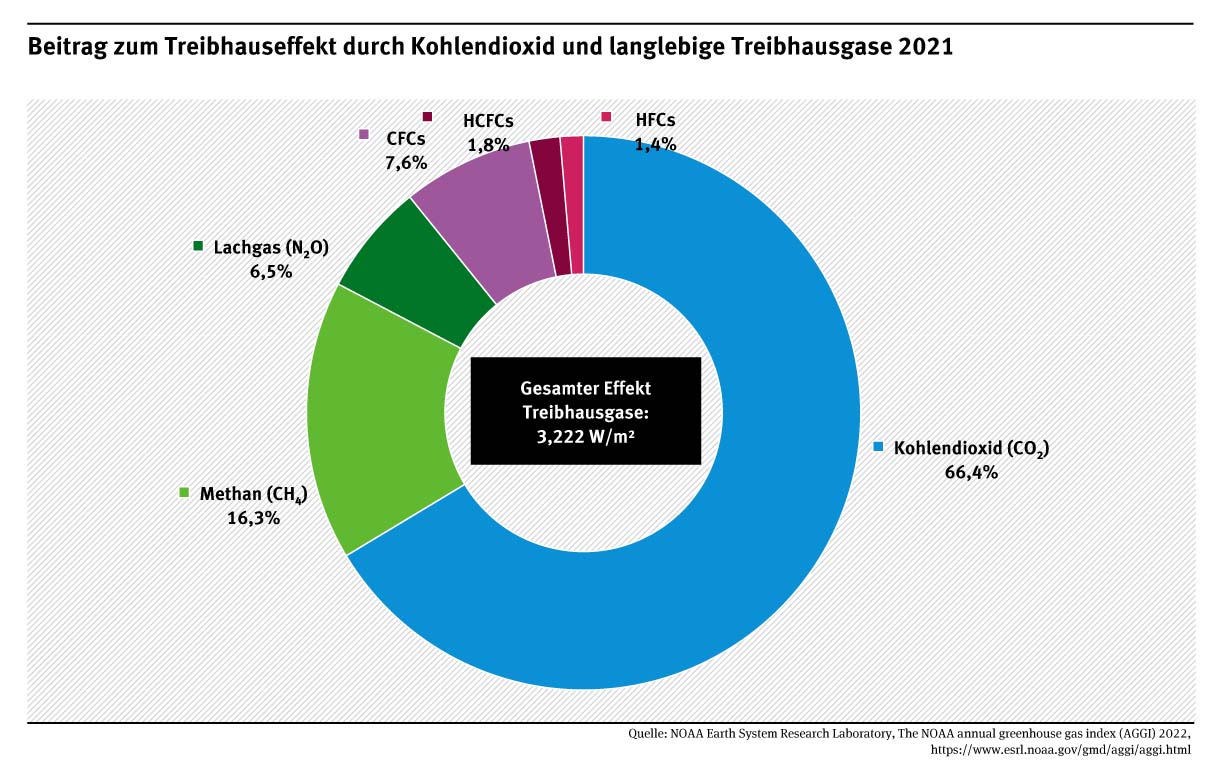 Abbildung 1 (
Abbildung 1 (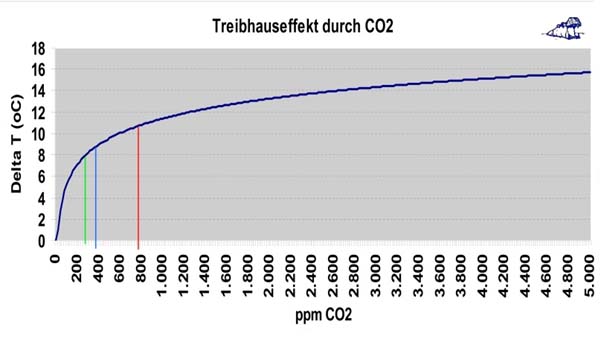 In der nachfolgenden Abbildung wird dieser logarithmische Zusammenhang zwischen dem atmosphärischen CO2-Gehalt und der Temperatur deutlich:
In der nachfolgenden Abbildung wird dieser logarithmische Zusammenhang zwischen dem atmosphärischen CO2-Gehalt und der Temperatur deutlich: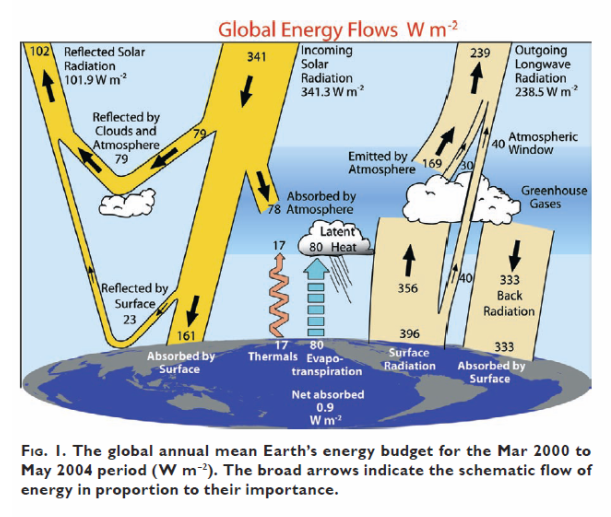 Abbildung 3: Das globale jährliche Energiebudget von März 2000 bis Mai 2004 in [W/m²]
Abbildung 3: Das globale jährliche Energiebudget von März 2000 bis Mai 2004 in [W/m²]