Von der Oberfläche in den Weltraum
Kevin Kilty
[Alle Hervorhebungen im Original]
Bei meiner Arbeit an der Serie „Das Energieungleichgewicht der Erde, Teile 1–3” habe ich einige Fragen offen gelassen, die ich zu einem späteren Zeitpunkt weiterverfolgen wollte. Dieser Zeitpunkt ist nun gekommen, unter anderem aufgrund einer kürzlich erschienenen Veröffentlichung, die meine Aufmerksamkeit erregt hat.
Hintergrund
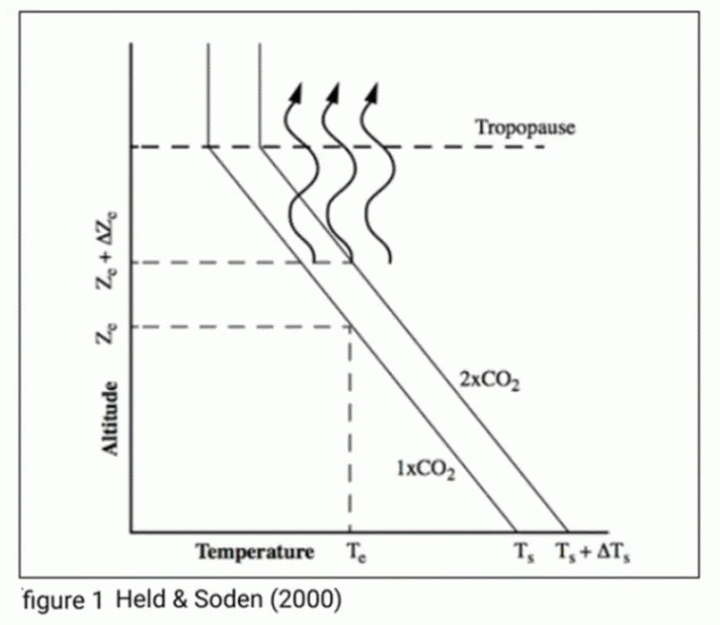
Wie im Beitrag „Earth’s Energy Imbalance Part II” zusammengefasst, lässt sich die Theorie der Reaktion auf die Strahlungsantriebe durch CO₂ am einfachsten anhand eines idealisierten, eindimensionalen Atmosphärenprofils erklären. Diese Erklärung ist in Abbildung 1 dargestellt und wird zum besseren Verständnis wie folgt erläutert:
Bei einer festen Te und einem festen Gradienten (Lapse Rate Γ) ergibt sich die Oberflächentemperatur zu: Ts = Te + ΓZe. In diesem einfachen Modell sind nur Änderungen in Ze von Bedeutung. Nun geht die Argumentation wie folgt:
Eine erhöhte CO₂-Konzentration in der Atmosphäre macht die Atmosphäre undurchlässiger für die von der Oberfläche ausgehende Infrarotstrahlung. Damit eine Atmosphäre mit doppelt so viel CO₂ oberhalb von Ze gleich transparent ist, um das Entweichen des durchschnittlichen Photons zu ermöglichen, muss Ze höher in der Atmosphäre liegen. Eine Verdopplung des CO₂-Gehalts macht die undurchlässigere Atmosphäre oberhalb von Ze+150 m gleich transparent. Der unveränderliche Gradient von 6,5 K/km bedeutet jedoch, dass die Temperatur bei Ze+150 m um etwa 1 K niedriger ist, was nach dem Stefan-Boltzmann-Gesetz einer Verringerung der ausgehenden Strahlung um etwa 4 W/m² entspricht (236,3 = σ 2544). Es entsteht ein Energieungleichgewicht, das die gesamte Atmosphäre und Oberfläche erwärmt.
Der hier genannte vertikale Temperaturgradient von 6,5 K/km {0,65°C/100 m} entspricht dem Gradienten in feuchtgesättiger Luft, d. h. bei Kondensation eines aufsteigenden Luftpaketes (die sog. „Feucht-Adiabate“). In trockener Luft beträgt dieser Gradient etwa 1°C / 100 m (die „Trocken-Adiabate“). Gerade in bodennahen Luftschichten, um die es ja hier geht, werden jedoch vertikale Gradienten erreicht, die weitaus größer sind. So kann sich der Boden bei vollem Sonnenschein bis auf 50°C aufheizen, während in einer Wetterhütte in 2 m über dem Boden vielleicht gerade mal 30°C gemessen werden. A. d. Übers.
Dies ist eine Analyse, die vollständig von einem Temperaturprofil mit einem unveränderlichen Temperaturgradienten abhängt. Lassen Sie mich nur am Rande anmerken, dass manchmal eine sehr einfache und stichhaltige Erklärung für ein imaginäres Problem relevant ist; aber das imaginäre Problem unterscheidet sich vom Problem der Relevanz. Ich denke, wir haben es hier mit einer solchen Situation zu tun.
Nichtsdestotrotz sind Elemente dieses eindimensionalen Denkens in der Klimadebatte allgegenwärtig.[1] Ich möchte nicht für Dr. Spencer sprechen, und vielleicht würde er dieses Thema näher ausführen, aber in einem Kommentar, den ich in „Earth’s Energy Imbalance, part II an Addendum” abgegeben habe, habe ich etwas erwähnt, das er an anderer Stelle in einer Mailingliste geschrieben hatte:
„… Roy Spencer hat gesagt, dass es beim Klimawandel nicht wirklich um das „Wetter“ geht, sondern hauptsächlich um den Strahlungstransport von der Oberfläche zum Weltraum, weshalb 1-D-Modelle genauso gut funktionieren wie globale Klimamodelle. Ich stimme dem zu, aber nur bis zu einem gewissen Grad. Ich denke, dass Konvektion und Advektion von den Tropen zu den Polen ebenfalls wichtig sind, aber nicht einmal in der Liste der Rückkopplungen aufgeführt sind. Lindzen hat in letzter Zeit betont, dass Transportprozesse in Richtung der Pole sehr wichtig sind. Die ganze Frage ist so kompliziert, dass sie zwangsläufig zu starken Meinungsverschiedenheiten führen wird …”
Aufgrund der Konzentration auf die 1-D-Geometrie ist eine wichtige Frage, die es zu untersuchen gilt: „Was sagt uns ein atmosphärisches Profil, eine 1-D-Säule, über den Wärmetransport von der Erdoberfläche zum Weltraum?”
Die kurze Antwort lautet, dass sie uns nichts Definitives sagt, solange sie nicht durch andere Informationen ergänzt wird. Der Grund dafür ist, dass eine beliebige Anzahl von Prozessen zu dem gleichen atmosphärischen Profil führen kann. Das Vorwärtsproblem, das von den Prozessen zum Profil führt, liefert eine eindeutige Antwort. Das inverse Problem, das von einem beobachteten Profil zurück zu den Prozessen führt, die es erzeugt haben, ist nicht eindeutig, sondern unendlich degeneriert. Dies ist das gleiche Problem, das ich als fatal für eine veröffentlichte Arbeit identifiziert habe, in der argumentiert wird, dass CO₂ keinen Einfluss auf die atmosphärische Temperatur hat.
Jedes kleine Teilchen, sagen wir jedes Kilogramm der Atmosphäre hat eine aktuelle Temperatur. Diese Temperatur reflektiert seine spezifische innere Energie.[2] Aus Lagrange-Sicht resultieren Änderungen der spezifischen inneren Energie aus der über die Zeit integrierten Wärmezufuhr, die dem Teilchen durch externe Quellen wie Strahlung und interne Quellen wie latente Wärme oder Dissipation kinetischer Energie zugeführt werden, abzüglich der Arbeit, die das Teilchen auf seinem Weg vom Ursprungsort zum aktuellen Ort gegenüber seiner Umgebung verrichtet hat. [3] Dies stellt eine enorme Informationsmenge dar. Es erklärt die Begeisterung für das 1-D-Modell, das Strahlungs-Konvektions-Gleichgewicht (RCE), und die Vorherrschaft der darauf basierenden Rückkopplungsanalyse.
Was ist mit RCE?
Obwohl ich das Konzept des Gleichgewichts für zweifelhaft halte, bezeichnen wir den Transport von Wärme in den Weltraum durch kombinierte Strahlung und Konvektion wie Caballero und Merlis als RCE. Der einzige Ort, an dem ich jemals die unveränderliche Temperaturabnahme von 6,5 K/km beobachtet habe, die das einfache Modell der Treibhauserwärmung benötigt, ist unter den Modellen in MODTRAN.[4] MODTRAN ist ein hervorragendes Lernwerkzeug, um zu untersuchen, wie die Struktur der Atmosphäre den Transport von thermischer IR-Strahlung beeinflusst. Es ist ein vernünftiger Rechner für thermische IR-Strahlung innerhalb bestimmter Grenzen. Es kann beispielsweise zeigen, dass eine Verdopplung des CO₂-Gehalts zu einer sofortigen Abnahme der ausgehenden Langwellenstrahlung (OLR) um 3,7 W/m² in der Tropopause führt, was wiederum einen Anstieg der Oberflächentemperatur um etwa 1 °C erfordert, um die OLR wieder auf ihren vorherigen Wert zu bringen, vorausgesetzt, es gibt keine Wasserdampf-Rückkopplung.
Die größte Einschränkung besteht darin, dass die uns zur Verfügung stehende Implementierung keine Erstellung eines benutzerdefinierten Decks der atmosphärischen Struktur zulässt. Stattdessen sind wir auf die Verwendung eines festen Satzes von Atmosphärenmodellen mit einigen wenigen Anpassungen für Wolken beschränkt. Alle diese Modelle beinhalten einen langen Temperaturbereich mit einer festen, konstanten Temperaturabnahme von etwa 6,5 K/km. Eine Änderung der Oberflächentemperatur eines Modells verändert die gesamte vertikale Säule um den gleichen Wert. MODTRAN erzwingt also eine unveränderliche Temperaturabnahme, und ein Modell, die US-Standardatmosphäre von 1976, weist eine konstante Temperaturabnahme von 6,5 K/km von der Oberfläche bis zum Weltraum auf. Es ist die Verkörperung des hier diskutierten einfachen Modells der Klimaerwärmung.
Die verschiedenen Modelle, die MODTRAN zur Verfügung stellt, sind alle fiktiv. Die US-Standardatmosphäre von 1976 beispielsweise begann 1922 als NACA-Standardatmosphäre. Sie war nicht als Instrument für Wetter und Klima gedacht, sondern sollte Input für operative und technische Probleme der Luftfahrt liefern. In den 1950er Jahren weiteten sich die Probleme der Luftfahrt auf die Raumfahrt aus. In Verbindung mit dem wachsenden Verständnis der oberen Atmosphäre führte dies ab 1953 zu einer Reihe von Aktualisierungen, die schließlich zur US-Standardatmosphäre von 1976 führten. Ich kenne den genauen Ursprung der anderen Modelle von MODTRAN nicht, aber sie alle entstanden offenbar aus technischen Anforderungen im Bereich der Waffen- und Instrumententechnik und nicht aus Wetter- und Klimafragen. Dennoch haben sie durch eine schleichende Ausweitung ihres Anwendungsbereichs Eingang in die Wetter- und Klimaforschung gefunden. So liefert beispielsweise die US-Standardatmosphäre von 1976 Gewichtungen (Beitragsfunktionen) für den GOES-R-Baseline-Imager. [5]
Da es nicht möglich ist, eine Modellatmosphäre zu entwerfen, führt die Verwendung von MODTRAN als Rechner für den Treibhauseffekt zu einer Inkonsistenz. Das angegebene Temperaturprofil kann nicht allein durch Strahlungstransport aufrechterhalten werden, wie Abbildung 2a zeigt. Andere Faktoren füllen implizit die Lücke, und ohne weitere Informationen können wir uns kaum vorstellen, wie diese wirken oder wie sie sich auf die Entwicklung des CO₂-Gehalts auswirken. Abbildung 2b zeigt, dass die Temperaturprofile in MODTRAN erfordern, dass Wärme tatsächlich als Advektion aus niedrigeren Breitengraden zugeführt wird, wenn beispielsweise das subarktische Wintermodell eine reale Bedeutung haben soll.
Unser Verständnis der Rückkopplungen in RCE umfasst, wie in Referenz [1] angegeben, wirklich nur den Teil „R“, während „C“ eine Vermutung bleibt.
Ein gelegentlicher Mitwirkender an Beiträgen auf WUWT hat einen interessanten und meiner Meinung nach cleveren Ansatz zum „C“-Teil von RCE gewählt. Ich möchte mich nicht für diesen Korrespondenten äußern oder ihn identifizieren, aber vielleicht stellt er freiwillig einen Link zu seiner Arbeit zur Verfügung, damit die Leser sie einsehen können. Anstelle dessen fasse ich zusammen, was ich für relevant halte.
Abbildung 2 impliziert, dass der Strahlungstransport quasi linear zunimmt, während die anderen, nicht näher bezeichneten Transportwege mit zunehmender Höhe abnehmen. Unter der Annahme, dass der andere Transport vollständig aus vertikalem Wärmetransport von der lokalen Oberfläche zum Weltraum durch Materialbewegung besteht, lässt sich eine Gesamt-Transportgleichung aus der Schwarzschild-Gleichung plus einem konvektiven Beitrag in parametrisierter Form schreiben. Ein Term wie λ = A∗(1 + Bx), wobei A und B Konstanten sind, stellt eine charakteristische Länge für die Strahlungsabsorption/-emission dar – größer um den Faktor (1+AB)/A in der Tropopause (x=1) als an der Oberfläche. Dieser λ-Faktor multipliziert die Schwarzschild-Transportterme. Ein Term wie κ = C ∗ (1 − Dx), multipliziert mit dem Temperaturgradienten, beschreibt den Rückgang der konvektierten (fühlbaren plus latenten) Wärme mit der Höhe. [6] Die numerische Lösung erfolgt über eine Variationsverfahren.
Der Ansatz ist nicht ohne Einschränkungen. Erstens berücksichtigt er keine advektive Wärme. Zweitens verwendet er ein lineares, graduelles Graumatmosphärenmodell, während sich die reale Atmosphäre davon unterscheidet, da Wasserdampf in Bodennähe sehr konzentriert ist. Drittens berücksichtigt er nicht ausdrücklich die Arbeit, die gegen die umgebende Atmosphäre in vertikaler Bewegung geleistet wird, obwohl ich vermute, dass dieser dritte Mangel durch die Wahl von C und D bis zu einem gewissen Grad gemildert wird. Trotz dieser Mängel lassen sich dennoch einige relevante Schlussfolgerungen ziehen.
Erstens erzeugt das 1-D-RCE-Modell keine konstante Temperaturabnahme, sondern eine systematisch von der Oberfläche zum Weltraum variierende. Wie der Korrespondent sagt: „Obwohl die Temperaturabnahme mit der Höhe überprüfbar erscheinen mag, sehen die tatsächlichen Diagramme visuell linear aus und deuten auf etwas anderes hin.“
Zweitens führen kleine Störungen von λ, k und der Oberflächentemperatur zu Empfindlichkeitswerten, die niedriger sind als man unter Verwendung von MODTRAN und der unveränderlichen Temperaturabnahme als Rechner vermuten würde.
Interessant!
Was ist mit dem Radiative/Advective Equilibrium (RAE)?
Auch hier geht es nicht unbedingt um Gleichgewicht, sondern lediglich um Wärmetransport durch Strahlung und Advektion. Die Arbeit von Caballero und Merlis konzentriert sich auf dieses Thema. Diese Arbeit beschreibt die Konstruktion und Erprobung eines sehr einfachen Modells der Wärmeübertragung am Nordpol. Die Autoren sagen, dass die Erwärmung der Pole als Reaktion auf globale Einflüsse noch nicht vollständig verstanden ist und dass dies…
„… das Interesse weckt an der Entwicklung eines minimalistischen RAE-Modells, das die grundlegenden physikalischen Eigenschaften des Klimas in hohen Breitengraden zuverlässig erfasst und als Gegenstück zum einspaltigen RCE für niedrigere Breitengrade dient …“
Man beachte insbesondere die implizite Dichotomie zwischen einem RAE-Modell für Polarregionen und einem RCE-Modell für niedrigere Breitengrade. Ich werde später noch einige Anmerkungen zu dieser Dichotomie machen, aber zunächst möchte ich mich auf eine Kritik des Inhalts des Artikels konzentrieren.
Um den Wärmetransport vollständig zu modellieren, müsste man mehrere Differentialgleichungen gleichzeitig lösen. Die wichtigste davon ist eine Aussage des ersten Hauptsatzes der Thermodynamik. Lassen Sie uns dies in Worten statt in Mathematik ausdrücken.
Wir interessieren uns für Veränderungen der inneren Energie eines Luftpakets, die sich aus der Summe von 1) Strahlungstransport (Schwarzschild) plus 2) Materialtransport (3-D-Skalarprodukt aus Materialgeschwindigkeit und Temperaturgradient) plus 3) einem Diffusionsterm zur Glättung der starken Temperaturgradienten (Frontmerkmale), die allein durch den Materialtransport entstehen, und schließlich 4) Wärmequellen und -senken ergeben.
Eine auf diesem komplexen Satz partieller Differentialgleichungen basierende Herangehensweise birgt mehrere Herausforderungen. Das geringste Problem ist zunächst einmal der dominierende Effekt auf den vertikalen Massentransport der Luftmasse, welcher der umgebenden Atmosphäre entgegenwirkt. Dies deutet darauf hin, dass zwei unterschiedliche, aber miteinander verbundene Temperaturen eine Rolle spielen: die absolute Temperatur für Kategorie 1 und die potentielle Temperatur für die Kategorien 2 und 3.
Zweitens ist das schwierigere Problem die Notwendigkeit einer 3D-Geschwindigkeit. Das bedeutet, dass man eine Aussage nach dem ersten Gesetz eines RAE-Modells nicht allein aus einer vertikalen Sondierung ableiten kann. Man benötigt eine vernünftige Lösung über einen 3D-Bereich. Dieses Problem ist rekursiv, zieht immer größere Regionen in Mitleidenschaft, und bald steht man vor der Aussicht, ein globales Klimamodell unzählige Male durchlaufen zu lassen, um eine Art faktorielles Experiment mit Ergebnissen vollständig zu füllen.
Die Autoren suchten stattdessen nach einem sehr einfachen Modell, das die Essenz des Energietransports in der Arktis erfasst, aber mit bescheidenen Ressourcen und guter Genauigkeit eine große Anzahl von Simulationen liefern kann.
Der einfache Weg, dies zu erreichen, bestand darin, ein auf die Breite beschränktes Modell mit einer einzigen Grenze am Übergang zwischen Arktis und mittleren Breiten zu erstellen und nur eine Energiebilanzgleichung zu verwenden. Tatsächlich wird die Arktis durch eine einzige vertikale Säule dargestellt. Die einzige Randbedingung konnte konstant gehalten werden, um numerische Experimente zu internen Prozessen in der Arktis durchzuführen, oder manipuliert werden, um numerische Experimente zu Faktoren außerhalb der Arktis durchzuführen. Der Artikel fährt fort, die Gültigkeit des Modells durch einen Vergleich mit Reanalyse- und globalen Klimamodellergebnissen zu belegen. Abschließend werden Schlussfolgerungen darüber gezogen, wie sich verschiedene in Zukunft zu erwartende Antriebe und Störungen auf das arktische Klima auswirken werden. Wer sich für Details interessiert, kann die Open-Source-Veröffentlichung zu Rate ziehen.
Ich befürworte das daraus resultierende Produkt nicht. Das Ziel der Autoren war es, den Klimawandel in der Arktis anhand der üblichen Antriebskräfte zu untersuchen: Veränderung der Oberflächenwärme, Veränderung der CO₂-Konzentration, Veränderung der spezifischen Feuchtigkeit, wobei die advektive Antriebskraft als etwas Neues hinzugefügt wurde. Meine Hoffnung war eine andere. Ich hatte gehofft, dass die advektive Wärmeübertragung als eigenständige globale Rückkopplung hinzugefügt würde. Meine Hoffnung wurde nicht erfüllt.
Die Dichotomie von RAE und RCE auf der Grundlage spezifischer Breitengrenzen steht nicht im Einklang mit dieser Hoffnung. Abbildung 3 zeigt, warum:
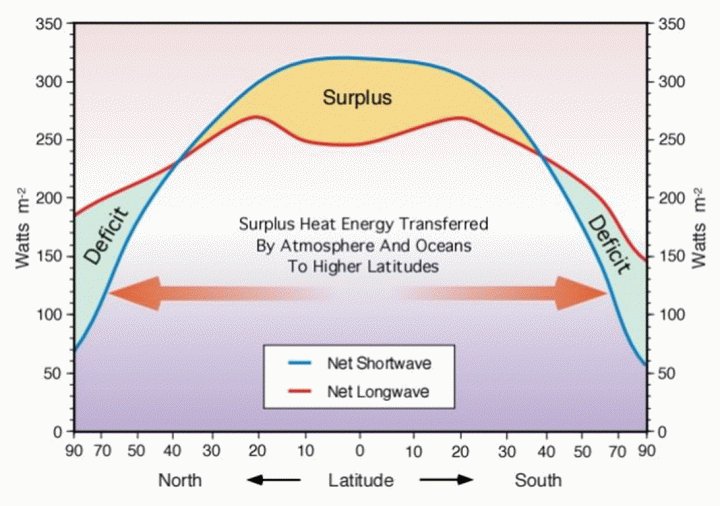
Abbildung 3: Durchschnittliche Wärmeüberschüsse/-defizite über ein Jahr auf der Erde und der damit verbundene advektive Wärmetransport, den ein stabiles Klima erfordert. [7]
Es liegt auf der Hand, dass bei einem Energieüberschuss in den Tropen und einem Defizit an den Polen die RCE allein ohne Advektion zu steigenden Temperaturen in den Tropen und sinkenden Temperaturen an den Polen führen würde. Advektion ist ein globales Phänomen, und es erscheint sinnvoll zu untersuchen, wie sich diese mit steigenden CO₂-Konzentrationen verändern wird.
Meine zweite Sorge betrifft die Beschränkung der Analysen auf einen Breitengradbereich, die von den Autoren mit Verweis auf andere Arbeiten begründet wird, die zeigen, dass…
„… die Pole zwar stark auf Einflüsse aus niedrigeren Breitengraden reagieren, das Gegenteil jedoch nicht zutrifft: Die Temperaturen in den mittleren Breitengraden werden in erster Näherung nicht von polaren Vorgängen beeinflusst …“.
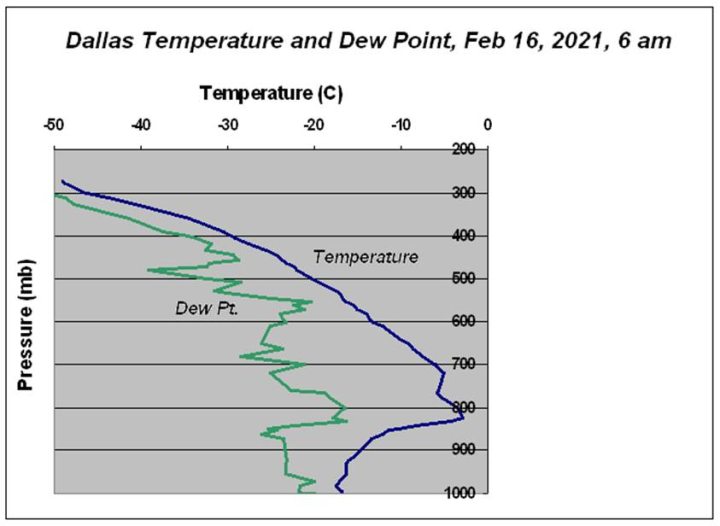
Abbildung 4 zeigt eine Sondierung aus Dallas-Fort Worth. Ein Texaner sagte einmal zu mir: „Zwischen Texas und dem Nordpol gibt es nichts außer einem Stacheldrahtzaun.“ Die Relevanz dieser Aussage für Abbildung 4 sollte offensichtlich sein. Strömungen von Flüssigkeiten, Luft und Meerwasser in die Polarregionen müssen durch Strömungen in die entgegengesetzte Richtung ausgeglichen werden. Abbildung 4 zeigt die Folge einer solchen Strömung. Die Oberflächentemperatur in Abbildung 4 beträgt -17 °C, und aus den Taupunktwerten geht hervor, dass das Mischungsverhältnis weniger als 0,8 g/kg beträgt und nach oben hin abnimmt. Die normalen Werte für das Mischungsverhältnis sind in dieser Jahreszeit zwei- bis viermal höher. Die polare Luftmasse hat weit südlich dieser mutmaßlichen Grenze zwischen subarktischer / mittlerer Breite erhebliche Auswirkungen gehabt.
Die sogenannte Oberflächen-Heizkörperlamelle
Caballero und Merlis identifizieren einen bedeutenden Prozess der Polarkühlung, der ihrer Meinung nach von einem atmosphärischen Profil wie dem in Abbildung 4 abhängt. Eine kalte Oberfläche mit einer Temperaturinversion und trockener Luft darüber kann ungehindert Strahlung in den Weltraum abgeben, da das atmosphärische Fenster für infrarote Wärmestrahlung offen ist. Die Atmosphäre kann sowohl durch Strahlung als auch durch Diffusion Energie mit der nahe gelegenen Oberfläche austauschen, und die Oberfläche, die einem schwarzen Körper ähnelt, strahlt dann effizient durch das Fenster in den Weltraum.
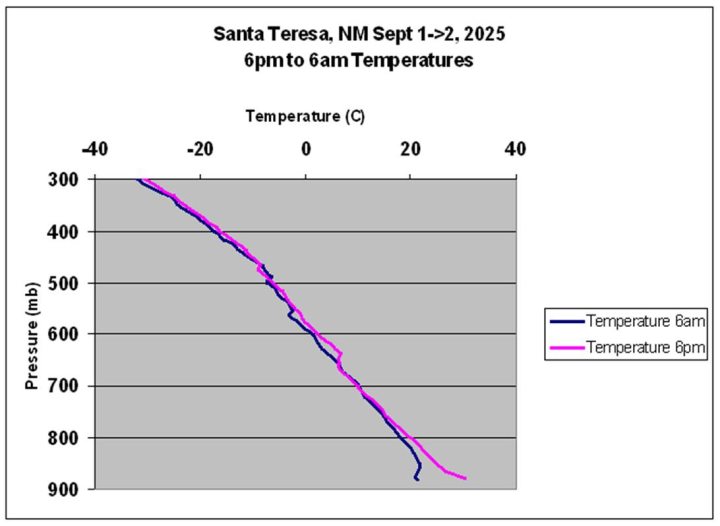
Es spielt keine Rolle, dass dies nicht die Funktion oder Wirkungsweise von Fins ist [8], denn der gleiche Prozess oder eine geringfügige Abwandlung davon findet weltweit statt. Selbst wenn zunächst keine Temperaturinversion vorliegt, wird diese durch trockene Luft und ein weit geöffnetes atmosphärisches IR-Fenster hervorgerufen. Abbildung 5 zeigt ein Beispiel aus dem Spätsommer in Santa Teresa, New Mexico, einem Ort und einer Situation, die denen ähneln, die ich in diesem Artikel vorgestellt habe. Über Nacht kam es zu einer systematischen Abkühlung der Luftsäule unterhalb von 730 mb und zur Entwicklung einer Inversion aufgrund der Strahlung des darunter liegenden Bodens – das Mischungsverhältnis ist mit etwa 10-12 g/kg in Bodennähe nicht einmal besonders trocken.
Während Abbildung 4 ein ungewöhnlich starkes Beispiel für die Südströmung zeigt, verdeutlicht Abbildung 6, dass im Winter flache Vorstöße polarer Luftströmungen tief in die Tropen hinein erfolgen. Diese nehmen nicht nur unterwegs Wärme auf, sondern öffnen aufgrund ihrer relativ trockenen Oberflächenluft auch das atmosphärische Fenster für IR-Strahlung direkt in den Weltraum. [9]
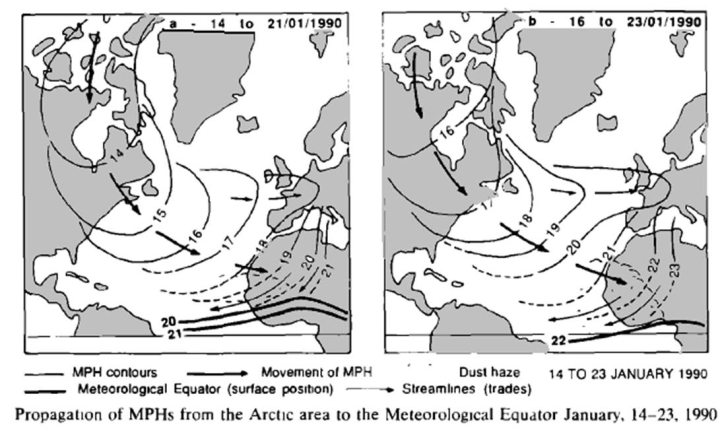
Abbildung 6. Zwei Beispiele für Vorstöße von Luft arktischen Ursprungs bis tief in die Tropen hinein. Ich habe das Original nur geringfügig verändert, indem ich die Landflächen schattiert habe, um die Bewegungsbahnen deutlicher zu machen.
Um diese schließlich in einen klareren Wärmeübertragungskontext zu stellen, zeigt Abbildung 7 eine numerische Simulation der Rayleigh-Benard-Konvektion, dem Prototyp-Modell der natürlichen Konvektion. Die untere Grenze wird erwärmt. Die obere Grenze wird gekühlt.
Man beachte, dass die Flüssigkeitsbewegung in diesem Fall keine gleichmäßige, regelmäßige Umwälzung der Flüssigkeit beinhaltet, sondern aus diskreten Flüssigkeitsklumpen besteht – rote steigen auf und blaue sinken ab. Das Auftreten von Klumpen im Gegensatz zu einer gleichmäßigen Umwälzung ist eine Funktion der Rayleigh-Zahl, die in diesem Beispiel Ra=10⁸ beträgt, was weit über dem Beginn der Flüssigkeitsumwälzung liegt.
Im Zusammenhang mit der Atmosphäre der mittleren Breiten sind die blauen Flecken mobile Kaltluftkörper, die entlang der Erdoberfläche in Richtung Äquator gleiten. Die roten Flecken sind die warme Gegenströmung von Luft/Feuchtigkeit, die in schräger Konvektion oder durch einen anderen Prozess, der Luft in höhere Breiten hebt und drückt, in Richtung Pol strömt. Die mobilen Kaltluftpakete nehmen relativ kühle Luft mit, die etwas Wärme und Feuchtigkeit in den mittleren Breiten und sogar in den Tropen aufnehmen kann, aber noch wichtiger ist, dass sie trockene Oberflächenluft mit sich führen, die an Orten, an denen es sonst keine gibt, ein offenes IR-Fenster bildet.
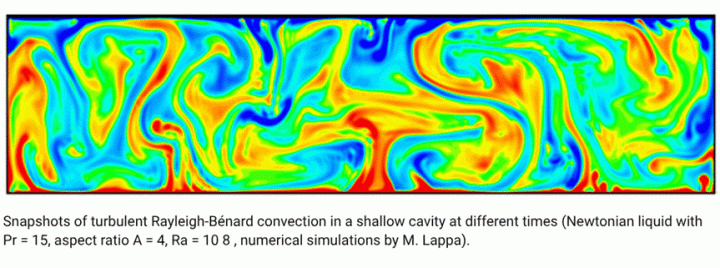
Abbildung 7. Numerische Simulation der Rayleigh-Benard-Konvektion. Bild von Lappa, Marcello. (2019). Über die Natur der Strömungsdynamik. Hochgeladen auf Researchgate von Marcello Lappa.
Schlussfolgerungen
Die Bemühungen von Caballero und Merlis, die diesen Aufsatz initiiert haben, haben nicht zu dem geführt, was ich mir erhofft hatte, vor allem weil ihr Ziel wie üblich darin bestand zu zeigen, wie CO₂ die Polarregionen erwärmen kann. Aus diesem Grund haben sie ein lohnenswertes Ziel nicht erreicht. Dieses Ziel besteht darin zu quantifizieren, wie die dadurch erwärmten Polarregionen Wärme von der Oberfläche in den Weltraum abgeben, da eine wärmere Oberfläche über die Stefan-Boltzmann-Rückkopplung mehr Wärme abstrahlt und dies in den trockensten Teilen der Atmosphäre mit einem breiteren atmosphärischen Fenster tut.
Die Advektion transportiert nicht nur Wärme über die Erdoberfläche dorthin, wo sie leichter von der Oberfläche in den Weltraum gelangen kann, sondern die sehr trockene Luft im Gegenstrom der arktischen und subarktischen Luftmassen aus den Polargebieten öffnet das atmosphärische Fenster zum Weltraum auf dem Weg zu wärmeren Regionen. Die globale Advektion verdient mehr Aufmerksamkeit, als ihr bisher zuteil geworden ist.
Referenzen und Anmerkungen
1. Caballero and Merlis, Polar Feedbacks in Clear-Sky Radiative–Advective Equilibrium from an Airmass Transformation Perspective, Journal of Climate, V 38, p. 3399, 15 JULY 2025
Diese Studie beginnt wie folgt, was meine Motivation für den vorliegenden Aufsatz war:
„Das Konzept des Strahlungs-Konvektions-Gleichgewichts (RCE) und seine Umsetzung in einem Ein-Säulen-Modell (Manabe und Strickler 1964; Manabe und Wetherald 1967) bilden die Grundlage für unser Verständnis und die Quantifizierung der Klimasensitivität.“
2. Die innere Energie entspricht der Wärmekapazität bei konstantem Volumen mal Temperatur plus einem beliebigen Referenzwert. Die Wärmekapazität ist eine Funktion der Temperatur, da bei höheren Temperaturen mehr Freiheitsgrade zur Verfügung stehen und Moleküle somit mehr Möglichkeiten haben, Energie zu speichern.
3. Wenn wir uns auf das Atmosphärenpaket als unser thermodynamisches System konzentrieren, lautet die Vorzeichenkonvention des Maschinenbaus, dass der dem Paket zugeführte Wärme positiv ist (und somit die entzogene Wärme negativ), während die Arbeit, die das Paket an seiner Umgebung verrichtet, positiv ist. Der erste Hauptsatz der Thermodynamik lässt sich als Gleichung in kleinen Mengen schreiben: δU = δQ – δW, wobei U die innere Energie ist. Physiker und Chemiker kehren die Vorzeichenkonvention für Arbeit im Allgemeinen um.
4. Die von mir verwendete Version ist an der University of Chicago erhältlich. Ich kenne nur eine weitere Version, die offenbar die gleichen Einschränkungen aufweist.
5. Timothy J. Schmit, et al, 2017, A Closer Look at the ABI on the GOES-R Series, Bulletin of the American Meteorological Society, 01 Apr 2017, p. 681-698. DOI: https://doi.org/10.1175/BAMS-D-15-00230.1
6. Der Wärmetransport durch bewegte Flüssigkeit wird mathematisch immer durch einen Term dargestellt, der in etwa einem Skalarprodukt (Vektor-Inneres Produkt) zwischen den Vektoren der Flüssigkeitsgeschwindigkeit und dem Temperaturgradienten entspricht. Daher ist die Konvektion als parametrisierte Geschwindigkeit (k-Term) und vertikaler Temperaturgradient in dieser eindimensionalen RCE-Formulierung angemessen. Das Vorhandensein einer positiven Arbeitsleistung eines Pakets beim Aufsteigen deutet jedoch darauf hin, dass die potentielle Temperatur angemessener ist.
In einem 3-dimensionalen Modell würde die horizontale Advektion von Wärme in jeder Höhe einen Term wie V·∇T beinhalten, wobei V der horizontale Geschwindigkeitsvektor ist, ∇ der horizontale Gradientenoperator (Grad von div, grad, curl fame) und der mittlere Punkt das horizontale Skalarprodukt darstellt. Die vertikale Komponente verwendet typischerweise Omega als Geschwindigkeitseinheit.
7. Adam Showman, J. Y-K. Cho, Kristen Menou, 2009, Atmospheric Circulation of Exoplanets, https://www.researchgate.net/publication/45884771; siehe beispielsweise Gleichungen 5a bis 5e. Man beachte, dass in 5e die advektiven/konvektiven Terme getrennt sind, wobei der konvektive Term in Omega (vertikale Geschwindigkeit in Druckkoordinaten) geschrieben ist. Omega ist viel kleiner als die horizontalen Komponenten, und der Versuch, es durch Beobachtungen unter Verwendung von 5c zu finden, führt meist zu Fehlern.
8. „Strahlungsrippen“ funktionieren ganz einfach, indem sie einen Weg mit geringer Leitfähigkeit für Wärme in einen großen Bereich bieten, wo die Wärme durch Flüssigkeitskonvektion abgeführt werden kann. Die typische Rippengeometrie ist ein schlechter Strahlungsemitter, weil jede Rippe einen großen Teil der anderen Rippen mit der gleichen Temperatur sieht.
9. Leroux, M, 1993, The Mobile Polar High a new concept explaining present mechanisms of meridional air-mass and energy exchanges and global propagation of palaeoclimatic changes, Global Planet Change, 7 69-93
Link: https://wattsupwiththat.com/2025/10/07/from-the-surface-to-space/
Übersetzt von Christian Freuer für das EIKE