Gibt es eine Zeitkonstante für die Absorption unserer CO2-Emission?

Anmerkung der Redaktion 

Der Beitrag von Dr. Beppler hat offenbar einen Nerv getroffen. Fast 500 Kommentare sind bis dato dazu eingegangen. Einer der Hartnäckigsten ist Herr Peter Dietze. Viele stimmen mit seinen Herleitungen der CO2 und seiner Verweilzeit, um nur einige seiner Punkte zu nennen, nicht überein. Andere hingegen durchaus. Wir wollen daher Herrn Dietze die Gelegenheit geben seine Überlegungen etwas breiter darzustellen.

Dipl.-Ing. Peter Dietze

In dem letzten EIKE-Beitrag von Dr. Beppler hatte sich eine Kontroverse um die Interpretation von IRF, der Impulsresponse-Funktion G(t) des IPCC-Modells mit 3+1 Zeitkonstanten tau sowie zu meinem C-Modell mit nur einem tau entwickelt. Da dies von erheblicher Relevanz (insbesondere für unsere Dekarbonisierung) ist und die Diskrepanzen geklärt werden sollten, jedoch die Kommentarfunktion beendet wurde, wurde hierzu der folgende Beitrag erstellt.

Wird C(t)=Summe(Ai exp(-t/taui)) – so wie unter https://cdatac.de/index.php/co2-conc/bern-cc/ und auch von Dr. Joos dokumentiert – auch für die Berechnung mit Emissionen benutzt, müssen diese (z.B. pro Jahr) jeweils als neuer Impuls zum Inventar der Atmosphäre addiert werden und sich mit C(t) reduzieren (d.h. anfangs sehr schnell und danach zunehmend langsam). Alldieweil reduziert sich auch das ältere CO2-Inventar parallel dazu langsam.

Damit kommen wir zu einem Faltungsintegral sowie zu der Erkenntnis dass beim IPCC die Abklingrate tau vom Alter des CO2 abhängt, was natürlich physikalisch unsinnig ist. Im Endeffekt äussert sich das in etwa so dass anfangs weniger als die Hälfte der Emission sehr schnell in die Senken geht und sich später gut die Hälfte quasi akkumuliert. Das ist offenbar der Grund für das effektive tau von 570 Jahren, welches ich bei Simulationsechnungen ermittelt habe – und auch ein Hinweis auf das Kumulationsmodell.

Fazit: Der längerfristig weit überhöhte ppm-Anstieg beim IPCC ist durch grob falsche Modellierung verursacht. Es gibt nur eine globale CO2-Zeitkonstante, und die kann nicht vom Alter der Emission abhängen.

Zunächst gilt für die Zusammenfassung paralleler Senkenflüsse aus der Atmosphäre

Inventar/tau=Inventar•(1/tau1+1/tau2+1/tau3)

wobei das anthropogen verursachte atmosphärische CO2-Inventar (proportional zu ppm-280) gemeint ist. Wenn man durch Inventar kürzt, ergibt sich ein summarisches tau für parallele Senken. Soweit eine Senke aus seriellen Boxen besteht (was beim CO2-Transport aus der ozeanischen Oberflächenschicht zur Tiefsee zumindest für den Anteil der Wirbeldiffusion ein Thema ist) gilt das tau gemeinsam für diese seriellen Boxen und geht so in die Summenformel ein. Möglicherweise ist die Unkenntnis dieses Sachverhalts der Grund dafür dass das falsche Bern-Modell (mitsamt dem garnicht existenten Ewigkeitsrest) selbst von vielen Fachleuten für sinnvoll gehalten wird.

Bei der anthropogenen Modellierung des weitgehend linearen Systems wird der etwa um den Faktor 20 größere natürliche überlagerte konstante Kreisfluss bei 280 ppm mit der „turnover time“ von nur etwa 4 a ausgeklammert. Soweit dieser sich durch die anthropogene Störung verändert, wird das als Anteil der anthropogenen Berechnung erfasst. Der anthropogen bedingte, zu ppm-280 proportionale Senkenfluss sowie der über 170 Jahre aufgrund unserer CO2-Emission beobachtete ppm-Verlauf von Mauna Loa führt zu einer effektiven globalen 1/e-Zeitkonstante von 55 Jahren.

Das Problem beim IPCC-Modell ist dass hier grob falsch mit verschiedenen IRF-Termen für zunehmendes Alter des restlichen CO2 ein stark steigendes tau angenommen wird, was ich bei ChatGPT widerlegt habe. ChatGPT brachte mich anhand der Frage nach dem Verlauf der CO2-Konzentration nach Nullemission auf den Nachweis dass altersabhängige (!!) Zeitkonstanten für die globale Absorption des CO2 aus verschiedenen Boxen der Atmosphäre NICHT gelten können – und dies hat eine immense Auswirkung auf die falsch berechneten ppm-Anstiege des IPCC (welche ja durch ein 5fach zu hohes (!) ECS den Klimaeffekt noch deutlich verschlimmern).

ChatGPT wies mich ausdrücklich darauf hin dass man für CO2 im Gegensatz zu radioaktivem Material keine feste Halbwertszeit (tau•ln(2)) angeben kann und deshalb von drei verschiedenen Bereichen (kurzfristig, mittelfristig und langfristig) ausgeht, was offenbar bedingt ist durch das fragliche Berner Wirbeldiffusionsmodell. In einem vierten Bereich wird darin tau unendlich, d.h. es entsteht eine remanente ppm-Erhöhung.

Ich brachte ChatGPT in Verlegenheit als ich fragte, wie denn das Alter des CO2 festgestellt werden kann, weil es ja sonst verschiedene Zeitkonstanten garnicht geben kann. Dazu erklärte ich trickreich, dass wir uns die Emission als einen Impuls denken können. Nach tau1 entfernt man das restliche CO2 schnell aus der Atmosphäre und emittiert es gleich wieder. Dann muss doch hierfür wieder das kurzfristige tau1 gelten und kein tau2, denn das System kann doch nicht altes und neues CO2 unterscheiden – also kann es kein tau2 und tau3 geben.

ChatGPT war verblüfft und attestierte mir, das sei eine intelligente (!) Überlegung. Natürlich versuchte es (weil es während einer Diskussion offenbar nicht dazulernt), mir dann durch ausgesuchte Textpassagen (vergeblich) klarzumachen warum die Modellierer doch mit verschiedenen Zeitkonstanten arbeiten.

Bei meinem Modell ist im Gegensatz zu IPCC die Atmosphäre nur EINE Box mit Pufferinhalt und EINEM tau, bedingt durch den globalen Senkenfluss und die einfache Differentialgleichung ist

dC/dt = Emission – C/tau.

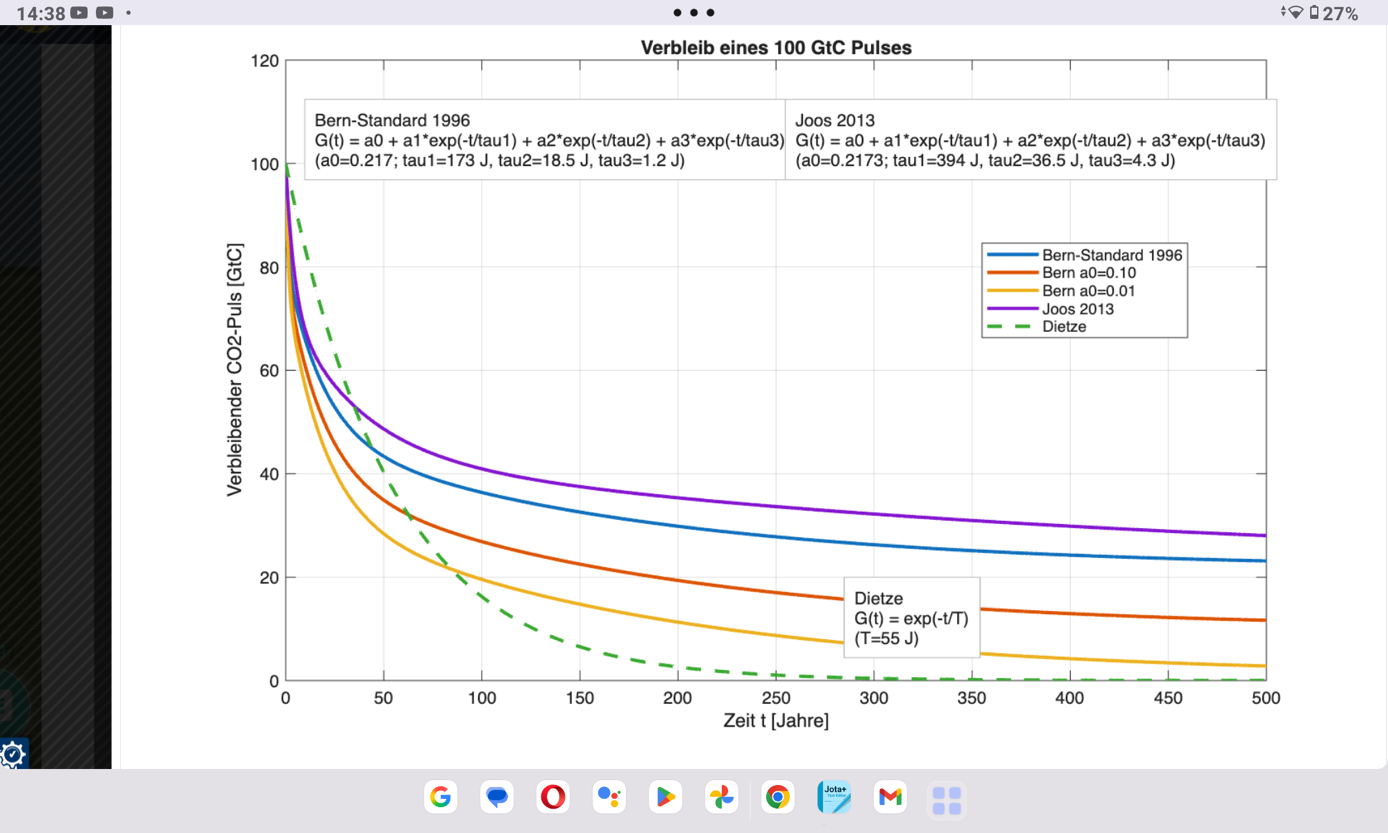
Herr Heß hatte dazu für die Impulsantwort IRF eine gute Vergleichsrechnung mit meinem tau=55 a gemacht (Abb.1), aber sich erstaunlichherweise jeder Kritik an IPCC enthalten („Ich habe das Bern-IRF-Modell anders verstanden: Das Bern-Modell ist nicht per se falsch, sondern eine Näherung. Mathematisch lässt sich eine Impulsantwort als Summe von Exponentialtermen darstellen“). Dabei ist doch mein tau=55 a die Realität und approximiert den ppm-Anstieg von Mauna Loa optimal, während die ppm beim Bern-Modell längerfristig erheblich zu weit ansteigen und sich eine Approximation mit einem völlig unrealistischen tau von 570 (!) Jahren ergibt.

In Abb.1 wurde gemäß Dr. Joos 2013 sowie mit dem Dietze-tau von 55 a nachgerechnet. Hier würde (abgesehen vom Remanent-Term von 21,73%, der auch für jede Emission gilt) anfangs z.B. für +140 ppm und tau=4,3 a der anthropogene Senkenfluss Inventar/tau=69,1 GtC/a (!!) sein und beim höchsten tau=394 a nach längerer Zeit nur 0,75 GtC/a – also nur etwa 1/100 (!!) des Anfangswerts (wobei natürlich noch der Boxenfaktor Ai zu berücksichtigen wäre). Beim Modell mit tau=55 a und 33% Zusatzpuffer beträgt der Senkenfluss anfangs realistische 7,2 GtC/a.

Hier wird deutlich, wie extrem das IRF-Modell die reale CO2-Physik durch G(t) vergewaltigt, zumal ja die Atmosphäre nicht in getrennte Boxen aufgeteilt werden kann, die nach einiger Zeit wegen unterschiedlichem tau ganz unterschiedliche ppm-Werte haben, welche dann (multipliziert mit dem Faktor Ai) addiert (!) werden.

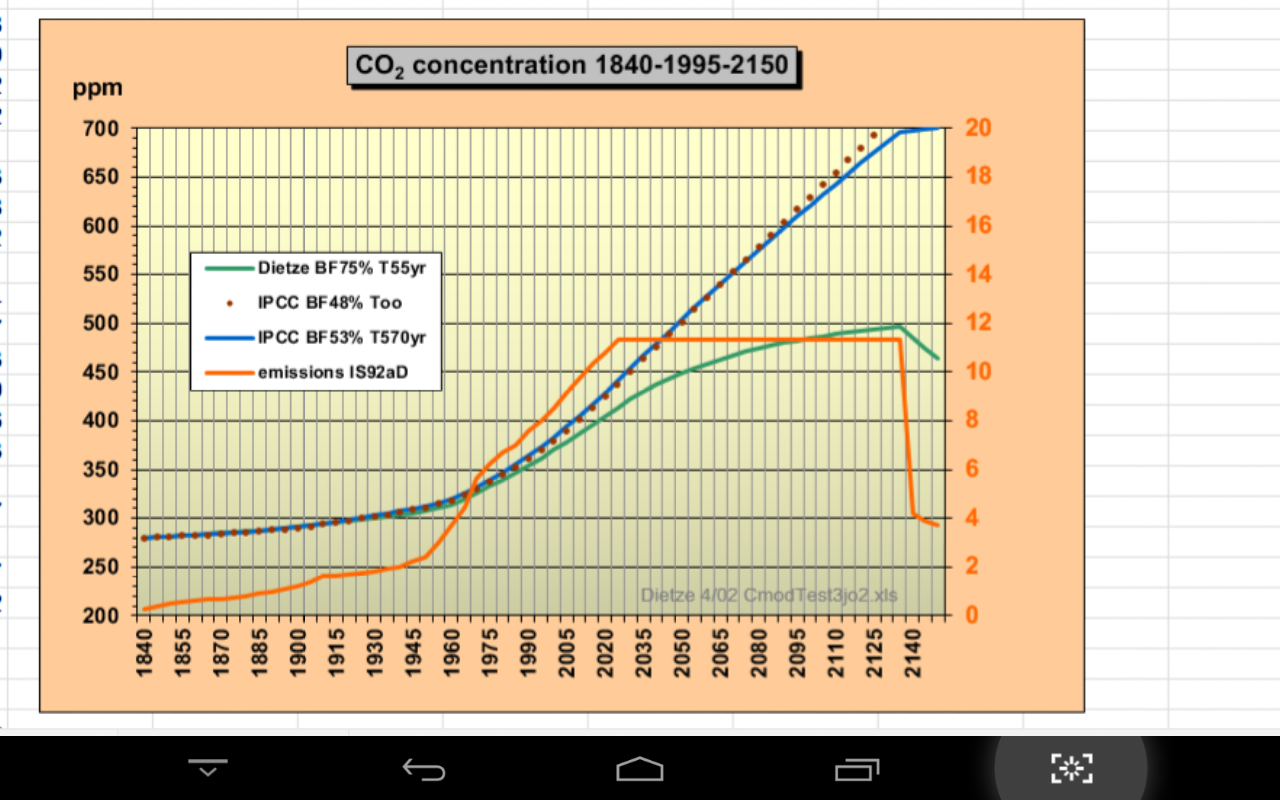
Dass sich in der Simulation für IPCC bis 2130 für den ppm-Anstieg ein effektives tau von 570 a ergibt, zeigt Abb.2, wo auch zu sehen ist dass bei einer Testrechnung mit Konstanthaltung der heutigen Emission über 110 Jahre CO2 wegen ansteigender Senkenflüsse nur bis auf max. harmlose 500 ppm ansteigt – beim IPCC wären es etwa 700 ppm.

Abb.1: Vergleichsrechnung von G(t) nach Nullemission, IPCC-IRT vs. Dietze von Herrn Heß.

Abb.2: Testrechnung für den weiteren ppm-Anstieg bei konstanter heutiger globaler Emission für 110 Jahre, Dietze vs. IPCC.