Genauigkeit von globalen Temperaturmessungen und deren „Anomalien“
von Michael Limburg
Abstract
Bestehende Unsicherheitsbewertungen und mathematische Modelle, die zur Fehlerabschätzung globaler durchschnittlicher Temperaturabweichungen verwendet werden, werden untersucht. Das Fehlerbewertungsmodell von Brohan et al. 06 [1] wurde als nicht umfassend und präzise genug befunden, um die Realität abzubilden. Dies wurde bereits für bestimmte Arten von zufälligen und systemischen Fehlern von Frank [2] [3], im Folgenden als F 10 und F 11 bezeichnet. Gleiches gilt für die vereinfachte behauptete Aufhebung zufälliger SST-Fehler durch CRU1, selbst für frühe Zeiten um 1850, als nur wenige Datensätze verfügbar waren. Diese Behauptung basiert lediglich auf der fast sicheren Annahme, dass die zufälligen Fehler früherer Messungen einen Mittelwert von Null haben und dass diese Fehler gleichmäßig verteilt sind.
Zur Verdeutlichung erläutere ich das allgemeine Verhalten der Anomalieberechnung in Bezug auf die Fehlerfortpflanzung. Es zeigt sich, dass die weithin angenommenen Fehlerreduktionsfähigkeiten eines Anomalie-Modells nur in einem Sonderfall gültig sind, aber im Allgemeinen den endgültigen systematischen Fehler – insbesondere in Zeitreihen – nicht reduzieren, sondern in den meisten Fällen sogar erhöhen. Darüber hinaus werden hier eine Vielzahl weiterer potenzieller systematischer Fehler genannt, von denen nur sehr wenige in der Literatur quantifiziert und korrigiert werden konnten, und das bisher auch nur teilweise. Dies wird ebenfalls aufgezeigt. In Anbetracht dessen sollte die minimale Unsicherheit für jede jährliche globale Durchschnittstemperatur nicht nur auf den hier beschriebenen Wert, d. h. mit einem 95-prozentigen Konfidenzintervall von ± 1,084 °C, erweitert werden, sondern mindestens um das 3- bis 5-fache. Somit löst sich die durchschnittliche globale Temperaturabweichung der letzten 150 Jahre in einem breiten, verrauschten Unsicherheitsband auf, das viel breiter ist als die gesamte angenommene Schwankungsbreite des 20. Jahrhunderts. Dieser Bericht zeigt, dass es aufgrund der Art der verfügbaren Daten, ihrer Quantität, Qualität und Methodik, wie es bei der Temperatur der Fall ist, nicht möglich ist, globale Zeitreihen mit der behaupteten Genauigkeit zu bestimmen. Das Ergebnis ist daher, dass alle auf diesen Daten basierenden Schlussfolgerungen und Korrelationen, die möglicherweise auf als wichtig erachteten Ursachen beruhen, innerhalb des Unsicherheitsbereichs liegen und daher nur als sehr grobe Schätzungen angesehen werden können. Daher bleibt jeder Versuch, diese Schwankung auf einen möglichen Antrieb zurückzuführen, reine wissenschaftliche Spekulation.
Vorwort
Diese Studie ist als Bericht verfasst und basiert auf verschiedenen früheren Arbeiten des Autors sowie zahlreichen anderen Veröffentlichungen über die Bemühungen zur Messung meteorologischer Temperaturdaten. Damit soll eher eine Literaturstudie vorgelegt werden als eigene Forschungsergebnisse. Dennoch sind alle in dieser Zusammenstellung enthaltenen Informationen und die daraus gezogenen Schlussfolgerungen neu und wurden nach bestem Wissen des Autors bisher (2014) noch nicht veröffentlicht.
Einführung
Die Mittelwertbildung geeigneter Messdaten und die Berechnung ihrer Anomalien zur Erkennung sonst verborgener Signale sind Standardwerkzeuge in wissenschaftlichen Verfahren unter Verwendung statistischer Verfahren. Diese Verfahren haben sich ebenso bewährt wie die von C.F. Gauß eingeführte Theorie der Fehlerfortpflanzung. Für globale Klima-Beobachtungen ist der Hauptindikator die lokale tägliche Lufttemperatur, die zu festen Zeiten oder durch Messung der Höchst- und Tiefsttemperatur an festen Standorten nebst anderen Parametern gemessen wird. Die so gesammelten Daten dienen als Grundlage für die Berechnung eines aussagekräftigen lokalen und später globalen Durchschnitts dieser Temperatur. Man möchte bestimmen:
a. einen absoluten Mittelwert dieser Daten, um Schätzungen der globalen mittleren Lufttemperatur zu ermöglichen, die z. B. zur Abschätzung von Energieübertragungsprozessen verwendet werden, und
b. eine Anomalie dieser Werte, d. h. die Differenz zwischen einem monatlichen oder jährlichen Mittelwert der lokalen Temperatur und einem Mittelwert der gleichen Station, der über einen Zeitraum von 360 Monaten bzw. 30 Jahren erfasst wurde. Der gewählte Referenzzeitraum wird meist anhand des WMO-Standardintervalls von 1961 bis 1990 festgelegt. Der gewählte Referenzzeitraum wird meist anhand des WMO-Standardintervalls von 1961 bis 1990 festgelegt.
Für beide berechneten Mittelwerte ist die Entwicklung im Zeitverlauf von großem Interesse, wobei z. B. die x-Achse die Jahre von 1850 bis 2011 und die y-Achse entweder den absoluten Mittelwert in °C oder die Differenz (Anomalie) zwischen dem tatsächlichen Jahres- oder Monatsmittelwert und einem ausgewählten geeigneten Referenzwert zeigt.
Durch die Anwendung dieser Verfahren konnten mehrere Klimaforschungsinstitute (GISS, NCDC, CRU) nachweisen, dass der berechnete Mittelwert der gesamten globalen Temperaturabweichung im letzten Jahrhundert um ca. 0,7 °C ± 0,1 °C gestiegen ist (siehe Abbildung 1). Da die Erdoberfläche zu 71 % mit Wasser bedeckt ist, wo Messungen der Lufttemperatur wesentlich schwieriger sind, ziehen es Klimawissenschaftler vor, stattdessen die Meerestemperatur (SST) zu messen und zu verwenden. Diese Daten variieren aufgrund der viel größeren Wärmeträgheit von Wasser viel weniger über die Fläche und nur wenig über den Tag hinweg. Da die Anomalien der SST recht gut mit den Anomalien der LAT (Landlufttemperatur) zu korrelieren scheinen, erscheint eine Vermischung der beiden einfach und möglich.
Um kleinste Schwankungen der Durchschnittstemperaturen innerhalb weniger Zehntelgrad Celsius zu ermitteln, sollten die Daten selbst und ihre statistische Unsicherheitsbehandlung eine endgültige Unsicherheit von ± 0,1 °C zulassen. Das Problem, mit dem die Experten konfrontiert waren, lag jedoch in der oft schlechten Qualität der häufig spärlichen historischen meteorologischen Daten. Daher scheint diese Aufgabe eher schwierig, wenn nicht sogar unmöglich zu bewältigen zu sein. Denn generell unterscheiden sich Unsicherheiten in meteorologischen Daten weder in ihrer Art noch in ihrer Klasse von denen in anderen Bereichen der wissenschaftlichen Arbeit sowie im Ingenieurwesen und Bauwesen, weshalb die üblichen Unsicherheitsalgorithmen und mathematischen Verfahren zur Behandlung von Unsicherheiten auf sie angewendet werden müssen. Wie oben erwähnt, zeigen die Studien, die sich mit dem genannten Problem befassen (die später in diesem Artikel zitiert werden), dass dies nur teilweise und bei wichtigen Daten nur auf eher selektive Weise geschehen ist. In dieser Studie wird versucht, einen Überblick über die wichtigsten Fehlerklassen zu geben, die berücksichtigt werden müssen, und es wird eine grobe Schätzung ihrer potenziellen Größenordnung gegeben. Schließlich wird ein weiterer Versuch unternommen, die mit jedem Mittelwert einhergehende Gesamtunsicherheit kurz zu quantifizieren.
Problemstellung, Beispiele
Die lokalen Lufttemperaturen werden seit mehr als 300 Jahren an einigen Orten der Welt zu meteorologischen Zwecken beobachtet (z. B. in Berlin seit 1701). Die täglichen Lufttemperaturen an Land werden meist durch mehrmalige Messungen zu festgelegten Zeiten an bestimmten Orten erfasst. In anderen Regionen wurden nur die Höchst- und Tiefsttemperaturen ohne Zeitangabe ermittelt.
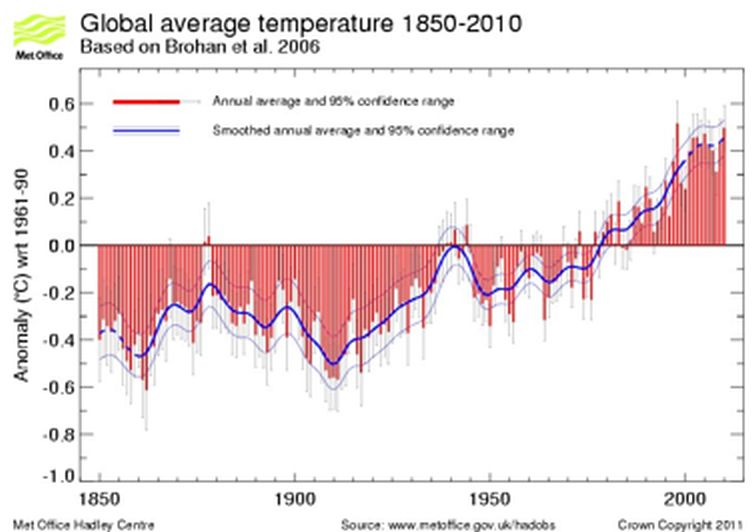
Abbildung 1: Globale durchschnittliche Temperaturabweichung von 1850 bis 2010, veröffentlicht auf der Website des MetOffice. Die roten Balken zeigen die globalen jährlichen durchschnittlichen Temperaturabweichungen in Bodennähe von 1850 bis 2009. Die Unsicherheitsbalken zeigen den 95-prozentigen Unsicherheitsbereich der Jahresdurchschnittswerte. Die dicke blaue Linie zeigt die Jahreswerte nach Glättung mit einem 21-Punkt-Binomialfilter. Der gestrichelte Teil der geglätteten Linie zeigt an, wo sie durch die Behandlung der Endpunkte beeinflusst wird. Die dünnen blauen Linien zeigen die 95 %ige Unsicherheit der geglätteten Kurve. Quelle: http://www.metoffice.gov.uk/hadobs/hadcrut3/diagnostics/comparison.html
Um störende Einflüsse durch direkte Sonneneinstrahlung, Wind und andere Störungen zu vermeiden, wird das verwendete Thermometer gegen seine Umgebung abgeschirmt und in einem Wetterschirm oder einer Wetterschutzwand untergebracht. Es ist seit jeher bekannt, dass diese Abschirmung eigene Eigenschaften hat, welche die gemessene Temperatur beeinflussen und somit keine direkte Messung der tatsächlichen Lufttemperatur ermöglichen, an der Meteorologen wirklich interessiert sind. Die Notwendigkeit eines akzeptablen Kompromisses führt jedoch dazu, dass diese Konstruktionen an den Standort angepasst werden, indem die durch diesen Kompromiss entstehenden Fehler akzeptiert werden. Zusätzlich zu diesen bekannten, aber nicht korrigierten Fehlern, die durch den Einsatz von Abschirmungen weltweit und im Laufe der Zeit entstanden sind, wurden unterschiedliche Verfahren (zur Ermöglichung der Algorithmen zur Berechnung einer Durchschnittstemperatur) zur Datenerfassung sowie unterschiedliche Konstruktionen der Abschirmungen verwendet.
Da das Ziel darin besteht, klimarelevante Signale zu extrahieren, die in lokal gemessenen Daten enthalten sein dürften, ist es für eine Temperaturmessstation erforderlich, dass längere statt kürzere Zeitreihen verwendet werden und dass diese Daten möglichst kontinuierlich gemessen werden. Zur besseren Erkennung und zum besseren Vergleich dieser Signale werden Anomalien berechnet. Das heißt, dass von den beobachteten Daten ein geeigneter Referenzwert abgezogen wird.
Wenn eine solche Station schon länger existiert, z. B. seit 50 oder besser 120 bis 150 Jahren mit kontinuierlichen Messungen, dann ist eine Zeitreihe und Anomalieberechnung für jeden einzelnen Monat oder jedes einzelne Jahr sinnvoll. Das Ergebnis kann zusammen mit allen anderen zu einer globalen mittleren Temperatur-Zeitreihe zusammengefasst werden wie in Abb. 1 dargestellt. Wie dort gezeigt, beinhaltet jede Anomalie auch ihre eigene Unsicherheit, wie durch den grauen Konfidenzbereich in Abbildung 1 (2) angezeigt, abgerufen am 21. April 2012 von http://www.cru.uea.ac.uk/cru/data/temperature/#sciref. Das Verfahren zur Berechnung dieser Anomalien wird vom britischen Met Office und anderen Organisationen beschrieben.
(2) Quelle: http://www.cru.uea.ac.uk/cru/data/temperature/#sciref Brohan , P., J.J. Kennedy, I. Harris, S.F.B. Tett und P.D. Jones, 2006: Unsicherheitsschätzungen bei regionalen und globalen beobachteten Temperaturänderungen: ein neuer Datensatz aus dem Jahr 1850. J. Geophysical Research 111, D12106, — Jones, P.D.,
New, M., Parker, D.E., Martin, S. und Rigor, I.G., 1999: Lufttemperatur und ihre Schwankungen in den letzten 150 Jahren. Reviews of Geophysics 37, 173-199. Rayner, N.A., P. Brohan, D.E. Parker, C.K. Folland, J.J. Kennedy, M. Vanicek, T. Ansell und S.F.B. Tett, 2006: Verbesserte Analysen der Veränderungen und Unsicherheiten der seit Mitte des 19. Jahrhunderts vor Ort gemessenen Meerestemperaturen: der HadSST2-Datensatz. J. Climate, 19, 446-469.
Rayner, N.A., Parker, D.E., Horton, E.B., Folland, C.K., Alexander, L.V, Rowell, D.P., Kent, E.C. und Kaplan, A., 2003: Global vollständige Analysen der Meerestemperatur, des Meereises und der nächtlichen Meereslufttemperatur, 1871-2000. J. Geophysical Research 108, 4407.
In den Daten, die beispielsweise auf der Website des Met Office (1) verfügbar sind, sind eine Reihe dieser Fehler oder Unsicherheiten definiert.
Das Ergebnis dieser Auswertung wie in Abbildung 1 dargestellt ist, dass die angegebene Gesamt-Unsicherheit der globalen Temperaturabweichung über den gesamten Zeitraum etwa ±0,15 °C bis ±0,1 °C beträgt. Diese kombinierte Unsicherheit entspricht einer Genauigkeit bis zur Grenze der instrumentellen Präzision (±0,1 °C) für die Lufttemperatur an Land (LAT) sowie für die Meerestemperatur (SST). Sie entspricht jedoch den Werten, die nur von geschultem Personal mit gut gewarteten und präzise kalibrierten Instrumenten für lokale Messungen erzielt werden können, oder übertrifft diese sogar. Da Temperaturdaten erfasst werden, die teils mehr als 100 Jahre zurückreichen und in verschiedenen Klimazonen mit Jahresmittelwerten zwischen etwa + 30 °C und etwa -35 °C gemessen wurden, wodurch ein Bereich von 65 °C abgedeckt wird, bedeutet diese Aussage, dass man bei der Bestimmung der globalen mittleren Temperaturabweichung eine Gesamtgenauigkeit von ±0,23 % bzw. ±0,15 % erreichen konnte. Normale Temperaturmessungen sind jedoch in der Regel viel ungenauer, oder, um es mit dem Begriff „Unsicherheit” zu sagen, ihre Unsicherheiten sind viel höher.
Darüber hinaus unterliegen die Rohdaten der lokalen Temperaturen einer Vielzahl von Einflüssen und weisen daher inhärente Fehler oder Abweichungen auf (3). Nur ein kleiner Teil davon, nämlich die echten Zufallsfehler, für die ein ausreichend großer Datenmenge zur Verfügung steht, kann durch die Anwendung statistischer Methoden der bekannten Fehlerfortpflanzungstheorie bestimmt und minimiert oder aufgehoben werden. Dabei handelt es sich in erster Linie und zum Teil nur um Ablesungs- und Messgerätefehler. Der größte Teil, die systematischen und groben Fehler müssen entweder sorgfältig korrigiert oder mit entsprechenden Fehlerbereichen versehen werden. Die Korrekturversuche der beteiligten Wissenschaftler zum Ausgleich systematischer Fehler, beispielsweise aufgrund des städtischen Wärmeinseleffekts (UHI) durch veränderte Landnutzung, sind aufgrund der enormen und oft unvollständigen Datenmengen nach bestimmten und wenigen Kriterien automatisiert und unflexibel. „Unflexibel” bedeutet, dass sie nur wenigen und starren Anforderungen folgen, die aufgrund mangelnder Kenntnisse über die Randbedingungen keine echten Korrekturen zulassen. Darüber hinaus sind die wenigen Korrektur-Algorithmen zwangsläufig schematisch angelegt. Die Korrektur erfolgt oft am Schreibtisch, ohne Vor-Ort-Besichtigung. Die erforderlichen Metadaten, welche die Randbedingungen der Rohdaten beschreiben, sind selten verfügbar. Daher führen die vorgenommenen Korrekturen oft zu falschen Ergebnissen. Andere wesentliche Kriterien werden nicht erfasst oder einfach wegdefiniert.
(3) Um die Art solcher Unsicherheiten zu beschreiben, verweisen Brohan et al. 2006 auf die philosophische Definition dieses Begriffs durch den ehemaligen Verteidigungsminister Donald Rumsfeld und machen sie sich zu eigen:
„Eine endgültige Bewertung von Unsicherheiten ist unmöglich, da es immer möglich ist, dass ein unbekannter Fehler die Daten verfälscht hat, und für solche Unbekannten kann keine quantitative Berücksichtigung vorgenommen werden. Es gibt jedoch mehrere bekannte Einschränkungen in den Daten, und es können Schätzungen der wahrscheinlichen Auswirkungen dieser Einschränkungen vorgenommen werden“ (Verteidigungsminister Rumsfeld, Pressekonferenz am 6. Juni 2002, London). Rumsfeld definiert dies wie folgt: „Es gibt bekannte Bekannte. Das sind Dinge, von denen wir wissen, dass wir sie wissen. Es gibt bekannte Unbekannte. Das heißt, es gibt Dinge, von denen wir jetzt wissen, dass wir sie nicht wissen. Aber es gibt auch unbekannte Unbekannte. Das sind Dinge, von denen wir nicht wissen, dass wir sie nicht wissen.”

Abbildung 2 Das linke Bild (Quelle [8]) zeigt verschiedene Screen-Designs des letzten Jahrhunderts – von links nach rechts: den französischen Screen, zum Vergleich einen Mann, dann den ursprünglichen Stevenson-Screen und die hohe Wild’sche Hütte, die in Russland verwendet wird. Das rechte Bild (Quelle [7]) zeigt von links nach rechts zwei neuere Stevenson-Screens [Wetterhütten; siehe Eingangsbild], die etwas größer sind als das Original, sowie eine Vielzahl runder moderner Gehäuse für elektronische Sensoren. Dabei ist zu beachten, dass nicht nur die Größe unterschiedlich ist, sondern auch die Höhe der Sensoren, die beim Stevenson-Screen zwischen etwa 1 m und 2 m und bei der russischen Hütte bis zu 3,2 m variiert.
Dies führt zu unterschiedlichen Ergebnissen, die jedoch nur auf die Messbedingungen zurückzuführen sind und nicht auf die Daten selbst. Aus diesem Grund enthalten die historischen Werte verschiedene Fehler, die darauf zurückzuführen sind. In der vorliegenden Studie untersuchen wir:
a. ob die angegebenen Fehlergrößen und Bandbreiten der Realität entsprechen und
b. ob und wie sie sich auf die Gesamtunsicherheit der globalen Temperaturabweichung auf der Grundlage der offiziellen IPCC-Bewertung auswirken.
Dabei verfolge ich einen Bottom-up-Ansatz, um beide oben genannten Punkte anzugehen: vom lokalen Messgerät bis zum endgültigen Durchschnittswert. Es beschreibt kurz die Probleme im Zusammenhang mit der Messung der Lufttemperatur an Land (LAT) und über der Meeresoberfläche (MAT, NMAT und SST). Anschließend werden die meisten möglichen Fehler ausführlich erörtert, die bei der Auslesung und weiteren Verarbeitung auftreten können. Es beschreibt außerdem die Verfahren und Algorithmen, die von der Wissenschaftsgemeinschaft zur Bearbeitung dieser Themen verwendet werden, und erwähnt die behaupteten Unsicherheiten.
Fehlerquellen und -arten
Meteorologische Messungen enthalten eine Vielzahl potenzieller und tatsächlicher Fehler. Es lohnt sich, dem Leser deren Definitionen in Erinnerung zu rufen. Man kann sie in zufällige Fehler und systematische Fehler oder Unsicherheiten einteilen.
Zufällige Fehler
Gemäß den deutschen VDI-Richtlinien (siehe VDI 2048 S. 36 und [9]) zu „Messunsicherheiten“ … werden zufällige Messfehler typischerweise als Schwankungen in der Größe definiert, die eine Gauß’sche Verteilung und einen Mittelwert von Null haben müssen. (Hervorhebung hinzugefügt) Mit anderen Worten: Die zufällige Unsicherheit wird durch die Populationsmerkmale der Unsicherheit selbst definiert und nicht durch ihre Auswirkungen auf die Messungen. Fehler, die sich anders verhalten, werden als nicht zufällig definiert. Und all diese Definitionen gelten nur, wenn mehrere bis viele wiederholte Messungen des gleichen Wertes vorgenommen werden – um den „wahren“ Wert μ herum, der in unserem Fall ti genannt wird. Die letztere Bedingung trifft bei meteorologischen Messungen so gut wie nie zu.
Systematische Fehler
Systematische Unsicherheiten unterscheiden sich von zufälligen Unsicherheiten, treten jedoch ebenfalls bei fast jeder Messung auf.
Gemäß den zuvor zitierten VDI-Richtlinien ((VDI 2048 S. 36) „… ist eine systematische Messunsicherheit es (siehe DIN 1319-1[1]) der Begriff für den Teil der Unsicherheit eines Messwerts x* vom wahren Wert μ, der aufgrund der Unvollkommenheit der Sensoren und des Messverfahrens durch konstante Einflüsse und Ursachen entsteht. Die systematische Messunsicherheit es würde den gleichen Wert annehmen. Die systematische Messunsicherheit es setzt sich aus der bekannten und messbaren systematischen Messunsicherheit es,b und der unbekannten und nicht messbaren Messunsicherheit es,u zusammen. Der Messwert wird wie folgt beschrieben:
x*=µ+er +es =µ+er +es,b +es,u
Mit anderen Worten, es handelt sich um Messabweichungen, die dazu führen, dass der Mittelwert vieler einzelner Messungen erheblich vom tatsächlichen Wert des gemessenen Merkmals abweicht. Wenn sie bekannt sind oder ausreichend genau und eindeutig geschätzt werden können, lassen sie sich korrigieren, indem die erforderliche Korrektur auf den Messwert angewendet wird. Ein sehr einfaches Beispiel für einen systematischen Fehler ist eine Uhr, die immer 5 Minuten nachgeht, wobei man einfach 5 Minuten zur angezeigten Zeit hinzufügen kann, um die genaue Zeit zu erhalten. Ist dies nicht möglich, müssen die Abweichungen ordnungsgemäß beschrieben, in Richtung und Größe geschätzt und als Unsicherheitsspanne zum Messwert addiert werden.
Dieses Uhrenbeispiel zeigt jedoch auch ganz einfach, dass sich Fehler in den zur Erstellung von Zeitreihen verwendeten Daten ganz anders verhalten als einzelne Daten. Um sie zu korrigieren, muss man nicht nur die Größe und Richtung des einzelnen systematischen Fehlers kennen, sondern auch den Zeitpunkt, zu dem er auftritt, und wie lange er wirkt. Nur dann kann er durch Anomalieberechnung ausgeglichen werden, da er sonst die Zeitreihe und ihren Trend 1:1 verzerrt.
Leider sind die systematischen Unsicherheiten in der Klimatologie nicht so einfach wie im obigen Uhrenbeispiel. Darüber hinaus kommen sie in verschiedenen Formen zur Variablen hinzu und lassen sich kaum vom wahren Wert unterscheiden. Betrachtet man insbesondere Zeitreihen, wie es in der Klimatologie der Fall ist, können sie sich auch als Funktion der Zeit entwickeln, wie dies beispielsweise typischerweise durch den UHI (Urban Heat Island Effect) angezeigt wird.
Die systematischen Unsicherheiten bei meteorologischen Messungen lassen sich in verschiedene Klassen einteilen, von denen oft alle oder einige bei der Messung lokaler Temperaturen auftreten. Sie stehen in Zusammenhang mit oder hängen ab von:
1. Thermometer oder Sensor
1.1. Bauweise
1.2. Anzeige
1.3. Alter
1.4. Austausch von Sensoren. Wie, was?
1.5. Schutz/Gehäuse/Abschirmung von Thermometer oder Sensor. Unterteilt in:
1.6. Die Konstruktion des Gehäuses selbst
1.7. Sein Zustand, Lackierung, Struktur usw.
1.8. Messhöhe über dem Boden
1.9. Lage in der umgebenden Landschaft gemäß z. B. CRN-Klimareferenznetz Klasse 1 bis 5 (5)
(5) US NOAA für CRN Climate Reference Network NOAAs National Climatic Data Center: Climate Reference Network (CRN). Abschnitt 2.2. des Climate Reference Network CRN. Standortinformationshandbuch: „Die idealste lokale Umgebung ist ein relativ großes und flaches offenes Gebiet mit niedriger lokaler Vegetation, damit der Blick auf den Himmel in alle Richtungen außer in den unteren Höhenwinkeln über dem Horizont ungehindert ist.“ Es werden fünf Standortklassen definiert – von der zuverlässigsten bis zur am wenigsten zuverlässigen.
2. Die Abdeckung der Stationen über Land und Meer. Unterteilt in:
2.1. Abdeckung über Land
2.2. Abdeckung über Meer
3. Verteilung der Messstationen über Land und Meer.
3.1. Nach Standort
3.2. Nach Höhe über Normal
4. Für Messungen der Meerestemperatur (SST) gibt es eigene Klassen. Diese lassen sich grob in folgende Gruppen einteilen:
4.1. Wasseraufnahme mit Eimer (siehe Abb. 3)
4.2. ERI (Engine Rear Intake) von Wasser
4.3. Differenz zwischen SST und MAT (Marine Air Temperature)
4.4. Messfehler zwischen verschiedenen Temperaturen und verschiedenen Sensoren
5. Zeitpunkt der Beobachtung. Unterteilt in:
5.1. Zeitpunkt der Beobachtung aufgrund des verwendeten Mittelwertalgorithmus
5.1.1. Max-Min-Methode
5.1.2. Mannheimer Methode
5.1.3. Sowjetische oder Wild-Methode
5.1.4. Sonstige
6. Dauer der kontinuierlichen Beobachtung
6.1. Mit oder ohne Unterbrechung 5US NOAA für CRN Climate Reference Network NOAAs National Climatic Data Center: Climate Reference Network (CRN). Abschnitt 2.2. des Climate Reference Network CRN.
Aus dem Standortinformationshandbuch: „Die wünschenswerteste lokale Umgebung ist ein relativ großes und flaches offenes Gebiet mit niedriger lokaler Vegetation, damit der Blick auf den Himmel in alle Richtungen außer in den unteren Höhenwinkeln über dem Horizont ungehindert ist.“ Es werden fünf Standortklassen definiert – von der zuverlässigsten bis zur unzuverlässigsten.

Abbildung 3 Verschiedene Arten von Eimern zur Messung der Oberflächentemperatur des Meereswassers, die bis zum Ende des 20. Jahrhunderts verwendet worden waren, um an Bord eines Schiffes Proben von Meerwasser zu entnehmen. Ein Beispiel für einen Messsensor (LIG-Thermometer; Quelle [10]) ist ebenfalls abgebildet.
Fehlererkennung und mögliche Behandlung
Die Qualität einzelner Bodenmessstationen wird in den USA vielleicht am besten durch die ausgezeichneten und unabhängigen Bewertungen erfasst, die 2009 von Anthony Watts [11] und seiner Gruppe von Freiwilligen durchgeführt wurden.(., Is the U.S. Surface Temperature Record Reliable?, The Heartland Institute, Chicago, IL 2009) Sie ist öffentlich zugänglich, d. h. bei Watts, und deckt das gesamte USHCN-Netzwerk von Bodenmessstationen ab. Aufgrund dieser umfassenden Studie wurden etwa 69 % der USHCN-Stationen mit einer Standortbewertung von „schlecht” und weitere 20 % mit „nur befriedigend” bewertet (6). „Schlecht” bedeutet, dass sie gemäß der Klassifizierung des US Climate Reference Network Rating Guide (CRN) eine Abweichung von der tatsächlichen Temperatur von >2 bis >5 °C aufweisen können. „Befriedigend” bedeutet gemäß der gleichen Klassifizierung eine Abweichung von > 1 °C. Diese und andere (7), weniger umfassende veröffentlichte Untersuchungen zu Mängeln der Stationen haben gezeigt, dass die Bedingungen für die Messungen der Bodenmessstationen in den USA alles andere als ideal sind. Wie F10 berichtet, gilt dies jedoch auch für Europa. Zitat: „Eine kürzlich durchgeführte großflächige Analyse der Qualität von Stationsreihen im Rahmen der Europäischen Klimabewertung [JCOMM 2006] zitierte keine Untersuchung zur Stationarität der Varianz einzelner Sensoren und stellte fest, dass „noch nicht garantiert werden kann, dass alle Temperatur- und Niederschlagsreihen in der Version vom Dezember 2001 hinsichtlich des Tagesmittelwerts und der Varianz für jede Anwendung ausreichend homogen sind”.
(6) Weitere Informationen hier: Watts, A., Is the U.S. Surface Temperature Record Reliable?, The Heartland Institute, Chicago, IL 2009
(7) Alle Studien, die von Frank abgeleitet wurden, sind dort aufgeführt:
Pielke Sr., R., Nielsen-Gammon, J., Davey, C., Angel, J., Bliss, O., Doesken, N., Cai, M., Fall, S., Niyogi, D., Gallo, K., Hale, R., Hubbard, K.G., Lin, X., Li, H. and Raman, S., Documentation of Uncertainties and Biases Associated with Surface Temperature Measurement Sites for Climate Change Assessment, Bull. Amer. Met. Soc., 2007, 913- 928; doi: 10.1175/BAMS-88-6-913.;
Davey, C.A. and Pielke Sr., R.A., Microclimate Exposures of Surface-Based Weather Stations, Bull. Amer. Met. Soc., 2005, 86(4), 497-504; doi: 10.1175/BAMS-86-4-497.
Runnalls, K.E. and Oke, T.R., A Technique to Detect Microclimatic Inhomogeneities in Historical Records of Screen-Level Air Temperature, J. Climate, 2006, 19(6), 959-978.
Pielke Sr., R.A., Davey, C.A., Niyogi, D., Fall, S., Steinweg-Woods, J., Hubbard, K., Lin, X., Cai, M., Lim, Y.-K., Li, H., Nielsen-Gammon, J., Gallo, K., Hale, R., Mahmood, R., Foster, S., McNider, R.T. and Blanken, P., Unresolved issues with the assessment of multidecadal global land surface temperature trends, J. Geophys. Res., 2007, 112 D24S08 1-26; doi: 10.1029/2006JD008229.
Jede der oben genannten Fehlergruppen weist eine Reihe von zufälligen und systematischen Fehlern auf, die sehr sorgfältig untersucht werden müssen. Allerdings konnten nur wenige davon berücksichtigt werden. Die Arbeiten von B 06, Karl 1994 et al [12] , Jones et al [13] ; [14] nennen nur die am häufigsten zitierten und untersuchen nur einige davon.
Laut Karl et al. lassen sich die zu korrigierenden Unsicherheiten wie folgt zusammenfassen:
1) städtische Wärmeinseln,
2) Änderungen der Beobachtungszeiten,
3) Änderungen der Instrumentierung,
4) Standortverlegungen und
5) unzureichende räumliche und zeitliche Stichproben.
Wie oben gezeigt, wurden mit dieser Liste jedoch nur wenige der potenziellen Unsicherheiten identifiziert. Darüber hinaus beschränken diese Autoren ihre Korrekturmaßnahmen auf die letzte Unsicherheit: unzureichende räumliche und zeitliche Stichproben.
Sie erklären:
„Unsere Analyse konzentriert sich auf diesen letzten Punkt, da bis vor wenigen Jahrzehnten der größte Teil der Erde nicht erfasst worden war. Wir betrachten zwei Arten von Fehlern: Fehler, die aufgrund fehlender Beobachtungen entstehen (Fehler vom Typ I aufgrund unvollständiger geografischer Abdeckung), und Fehler, die aufgrund unvollständiger Stichproben innerhalb von Gitterzellen (oder Mittelungsbereichen) mit Beobachtungen entstehen (Fehler vom Typ 2 innerhalb von Gitterzellen).
… Es ist klar, dass dies nur ein Teil aller Fehler und Verzerrungen ist, die die Berechnung der hemisphärischen und globalen Temperaturtrends beeinflussen und die in jeder umfassenden Fehleranalyse berücksichtigt werden müssen.“
Diese Aussage ist sehr zutreffend, denn auf Seite 1162 heißt es:
„Leider wird es niemals möglich sein, Gewissheit über das Ausmaß der Fehler zu erlangen, die aufgrund unvollständiger räumlicher Stichproben in die historischen Aufzeichnungen eingeflossen sein könnten, da wir niemals die tatsächliche Entwicklung der räumlichen Muster der Temperaturänderung kennen werden.“
B 06 Die andere wichtige Studie untersuchte die folgenden Unsicherheitsquellen:
Stationsfehler: Die Unsicherheit einzelner Stationsanomalien.
Stichprobenfehler: Die Unsicherheit eines Gitterfeldmittelwerts, die durch die Schätzung des Mittelwerts aus einer kleinen Anzahl von Punktwerten verursacht wird.
Verzerrungsfehler: Die Unsicherheit bei großräumigen Temperaturen, die durch systematische Änderungen der Messmethoden verursacht wird.
Ungeachtet dieser Aussage sind die einzigen von den Autoren untersuchten systematischen Unsicherheiten der städtische Wärmeinseleffekt (Urban Heat Island Effect, UHI) und eine mögliche Veränderung der Sensoren. In Bezug auf den UHI folgen sie Jones [13] (8) und Folland [15] (9).
(8) Nature 347 , S. 169 ff.
(9) Zitiert aus „Die Unsicherheiten bei der Bias-Korrektur werden nach (Folland et al., 2001) geschätzt, die zwei Verzerrungen in den Landdaten berücksichtigten: Urbanisierungseffekte (Jones et al., 1990) und Änderungen der Thermometerbelichtung (Parker, 1994). Urbanisierungseffekte: Die vorherige Analyse der Urbanisierungseffekte im HadCRUT-Datensatz (Folland et al., 2001) empfahl eine 1σ-Unsicherheit, die von 0 im Jahr 1900 auf 0,05 °C im Jahr 1990 stieg (linear extrapoliert nach 1990) (Jones et al., 1990). Seitdem wurden Forschungsergebnisse veröffentlicht, die darauf hindeuten, dass der Urbanisierungseffekt sowohl zu gering ist, um nachgewiesen zu werden (Parker, 2004, Peterson, 2004), als auch, dass der Effekt bis zu ≈ 0,3 °C pro Jahrhundert beträgt (Kalnay & Cai, 2003, Zhou et al., 2004).
Lufttemperatur über dem Meer (MAT) und Meerestemperatur
Die Erdoberfläche ist zu 71 % von Ozeanen bedeckt, etwa 80 % der südlichen Hemisphäre und etwa 60 % der nördlichen Hemisphäre. Darüber hinaus sind die Ozeane mit ihren Strömungen und Winden die Hauptquelle für unser Wetter, sowohl kurzfristig als auch langfristig. Noch wichtiger wäre eine kontinuierliche Überwachung der Lufttemperatur auf See, die geografisch gleichmäßig verteilt sein sollte. Dies ist jedoch nicht möglich. Es müssten zahlreiche Instrumente installiert, gewartet und überwacht werden, aber dies auf Schiffen zu tun (abgesehen von den wenigen Inseln mit ihrem eigenen Mikroklima) bedeutet, dass man unbequeme Kompromisse eingehen muss.

Abbildung 4: Die Karte mit kleinen Punkten zeigt die Anzahl und Verteilung der in der ersten Januarwoche 2000 gesammelten SST-Daten [16]. Man sollte bedenken, dass der Verkehr auf allen Ozeanen noch nie zuvor so intensiv war. Das Bild oben rechts zeigt ein Containerschiff mit einer Brückenhöhe von etwa 25 m und einer Tiefe von 10 bis 15 m. Das Bild unten rechts zeigt ein deutsches Segelschiff aus der Zeit um 1900, die Atalanta, mit einer geringen Deckshöhe von etwa 1,5 m.
Schiffe sind für die Fahrt gebaut, abgesehen von Ausnahmen wie Feuerschiffen. Daher ändern sich ihre Abmessungen sowie ihre Höhe ständig, wenn Schiffe beladen oder unbeladen fahren. Darüber hinaus ändern sich die Geschwindigkeit relativ zur ruhigen Luft und der Zeitpunkt der Beobachtung.
Daher bevorzugen die meisten Klimatologen die SST gegenüber der MAT oder NMAT, obwohl sie sich der sehr unterschiedlichen Eigenschaften von Meerwasser und Luft voll bewusst sind. Sie gehen jedoch davon aus, dass sich die Anomalien beider Temperaturen in Zeitreihen ziemlich gleich verhalten.
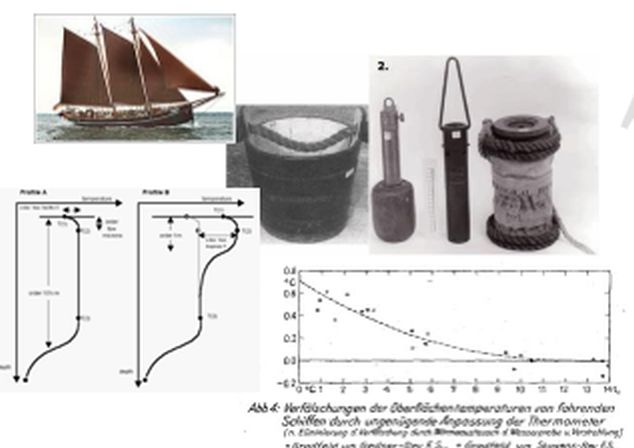
Abbildung 5: Von links oben nach rechts unten. Eines der letzten Handelssegelschiffe, das um 1900 in Hamburg gebaut wurde, um in den Nordatlantik zu fahren, mit niedriger Deckshöhe. Unten: Zwei Messungen in ruhigem Wasser, die die Schwankungen der Meerestemperatur in Abhängigkeit von der Tiefe zeigen. Oben rechts: Vier verschiedene Eimer, die von einem Seemann ausgeworfen und nach Berührung der Meeresoberfläche wieder eingeholt wurden [10]. Sie sollten Wasser in einer Tiefe von etwa 1 m auffangen. Die tatsächliche Tiefe bleibt unbekannt. Unten links: Schwankung der Wassertemperatur, gemessen in ruhigem Wasser in Abhängigkeit von der Tiefe [17]. Unten rechts: Zeitliche Reaktion eines Thermometers, das im Herbst im Skagerrak in einen Eimer mit Wasser getaucht wurde [18]. Nach 10 Minuten ist ein Gleichgewicht erreicht, und diese Temperatur sollte aufgezeichnet werden.
Jones geht daher davon aus, dass sich die SST wie die MAT in 10 m Höhe verhalten könnte (Jones et al. 1990, S. 174 und 175). Es werden jedoch keine Belege für diese Annahme angeführt. Stattdessen gibt es einige Studien, die genau das Gegenteil zeigen. So zeigten beispielsweise Christy et al. [19] anhand von Daten von festen Bojen in tropischen Gebieten ab 1979, dass deren SST einen leicht negativen Trend von -0,06 °C pro Jahrzehnt aufweisen, während die gleichzeitig gemessene MAT (und NMAT) einen Trend von +0,13 °C pro Jahrzehnt aufwiesen. Auch Kent et al. [20] haben zu diesem Thema geforscht und berichtet, dass die MAT in höheren nördlichen Breiten im Nordatlantik typischerweise um 1,5 °C (S. 11) über der SST liegt.
In Bezug auf die beobachteten oder angenommenen Unsicherheiten schrieb der Wissenschaftler John Kennedy vom Met Office(10):
„Eine einzelne SST-Messung von einem Schiff hat eine typische Unsicherheit von etwa 1–1,5 K. (Kent und Challenor (2006), 1,2 ± 0,4 K oder 1,3 ± 0,3 K; Kent et al. (1999), 1,5 ± 0,1 K; Kent und Berry (2005), 1,3 ± 0,1 K und 1,2 ± 0,1 K; Reynolds et al. (2002), 1,3 K; Kennedy et al. (2011a), 1,0 K; Kent und Berry (2008) 1,1 K. Diese Analysen basieren auf dem moderneren Teil der Aufzeichnungen. Es wurden keine Studien durchgeführt, um festzustellen, ob sich die Größe dieser Fehler im Laufe der Zeit systematisch verändert hat. Es sollte auch beachtet werden, dass nicht alle Messungen von identischer Qualität sind. Einige Schiffe und Bojen nehmen Messungen von viel höherer Qualität vor als andere…und weiter unten: .…
(10) Quelle: Met Office Hadley Centre observations datasets „Uncertainty in historical SST data sets“ http://www.metoffice.gov.uk/hadobs/hadsst3/uncertainty.html
Für Schiffe stellten Kent und Berry fest, dass die zufällige Fehlerkomponente bei etwa 0,7 K und die systematische Beobachtungsfehlerkomponente bei etwa 0,8 K lag. Kennedy et al. (2011a) stellten fest, dass die zufällige Fehlerkomponente bei etwa 0,74 K und die systematische Beobachtungs-Fehlerkomponente bei etwa 0,71 K lag. Addiert man die Fehler quadratisch, ergibt sich eine kombinierte Beobachtungs-Unsicherheit von etwas mehr als 1 K, was mit früheren Schätzungen übereinstimmt. Für Treibbojen schätzten Kennedy et al. (2011a) die zufällige Fehlerkomponente auf etwa 0,26 K und die systematische Beobachtungs-Fehlerkomponente auf etwa 0,29 K. Die entsprechenden Werte von Kent und Berry lagen bei 0,6 bzw. 0,3 K. Es wurde angenommen, dass die systematische Fehlerkomponente für jedes Schiff unterschiedlich ist, sodass dieses Modell allein die Auswirkungen weit verbreiteter systematischer Fehler nicht erfasst.
Sie gingen ferner davon aus, dass die systematische Verzerrung modernerer ERI-Daten (Engine Rear Intake, d. h. Kühlwasser, das zur Kühlung der Motoren verwendet wird) gegenüber Bucket-Daten (Buckets sammeln Wasser manuell von Seeleuten an Bord ihrer Schiffe) im Allgemeinen -0,3 °C (bezogen auf den Monatsdurchschnitt) betragen könnte. Dies wäre insbesondere dann der Fall, wenn die Lufttemperatur deutlich niedriger ist als die Wassertemperatur. Darüber hinaus merkten sie an, dass sie Eimer-Daten gegenüber ERI-Daten bevorzugen, da sie zuverlässiger zu sein scheinen. Das Problem dabei ist, dass weitgehend unbekannt ist, welches Verfahren in den letzten 150 Jahren verwendet wurde. Während Parker, Jones und Reynolds davon ausgehen, dass bis 1941 überwiegend Eimer-Daten verwendet wurden und danach die Verwendung von Eimern ziemlich schnell eingestellt wurde, zeigen andere Beobachtungen eine solide Mischung aus beiden Verfahren bis Ende der 1980er Jahre, die sogar bis zum Jahr 2005 zunahm. Aber z. B. [21] Folland 2005 stützte sein gesamtes Korrekturprogramm auf diese Annahme. Zwar wurde die Eimer-Verfahren im Laufe der Zeit durch die ERI-Verfahren und die aufkommende Bojen-Verfahren ersetzt, aber wie Abbildung 3 – insbesondere das untere Bild – zeigt, gab es bis in die letzten Jahre einen relativ großen Anteil an Eimer-Daten.
Ergebnisse und implantierte Korrekturmethoden
Mittelwertbildung absoluter Daten, Vorteile und Grenze
Verhalten von Anomalien und Fehlern in Zeitreihen und deren Grenzen
Der Grund, warum Zeitreihen von Anomalien bevorzugt werden, liegt darin, dass in vielen Wissenschaften Anomalien unabhängiger Größen berechnet werden, um gemeinsame Trends, Korrelationen oder allgemein „Signale” zu ermitteln, die möglicherweise leichter zu finden und zu quantifizieren sind als der Vergleich absoluter Zeitreihen einzelner Daten. Dies gilt insbesondere für die Klimatologie, wo man es mit sehr unterschiedlichen Original-Temperaturdaten zu tun hat. Aus diesem Grund schreiben die Autoren von NCDC-NOAA [22] in einer Erklärung, warum sie Anomalien bevorzugen (in Absatz 3) (Quelle: http://www.ncdc.noaa.gov/cmb-faq/anomalies.php, Absatz 3) …. Referenzwerte, die auf kleineren [lokaleren] Skalen über denselben Zeitraum berechnet werden, bilden eine Basislinie, von der aus Anomalien berechnet werden. Dadurch werden die Daten effektiv normalisiert, sodass sie verglichen und kombiniert werden können, um Temperaturmuster in Bezug auf das, was für verschiedene Orte innerhalb einer Region normal ist, genauer darzustellen. Und in Absatz 4 liest man:
„Anomalien beschreiben die Klimavariabilität über größere Gebiete genauer als absolute Temperaturen und bieten einen Bezugsrahmen, der aussagekräftigere Vergleiche zwischen Standorten und genauere Berechnungen von Temperaturtrends ermöglicht.“ (Fettdruck hinzugefügt)
Der erste Teil des Satzes in Absatz 3 erklärt genau, warum Anomalien bevorzugt werden, aber der fettgedruckte Teil von Absatz 4 ist im Allgemeinen falsch. Anomalien sind in den meisten Fällen weniger genau als die absoluten Temperaturen. Denn beide Werte enthalten zufällige und systematische Messfehler, wobei letztere in Zeit, Richtung und Größe variieren. Es gibt keinen Grund anzunehmen, dass diese Fehler während des Referenzzeitraums (Normalzeitraum) mit den Fehlern in anderen täglichen Daten oder deren Tages-, Monats- oder Jahresmittelwerten identisch oder auch nur ähnlich sind. Dies mag zwar der Fall sein, bleibt jedoch eine Ausnahme. Darüber hinaus verleiht die Berechnung der oft geringen Unterschiede jedem Fehler ein viel größeres Gewicht, als dies bei einem Vergleich mit den absoluten Daten allein der Fall wäre.
Daher lohnt es sich zu untersuchen, ob die Berechnung der Unterschiede (Anomalien) zwischen zwei Messdaten deren potenzielle Fehler aufhebt, insbesondere deren systematische Fehler. Diese Frage wird oft mit einem klaren „Ja” beantwortet, unabhängig davon, wer in der Welt der Wissenschaft oder Technik gefragt wird. Aber ist diese Antwort wirklich so zutreffend, wie viele Menschen glauben? Es ist hilfreich, sich die folgende einfache Formel anzusehen:
Da der Mess- oder Referenzwert t₂ vom Messwert t₁ abgezogen wird und sowohl t₁ als auch t₂ aus ihrem „tatsächlichen“ Wert 𝜏₁ bzw. 𝜏₂ plus einem Fehler von ε₁ bzw. ε₂ bestehen, kann man sagen, dass
t1 =𝜏1 ±e1 and t2=𝜏2 ±e2. (1)
Die Differenz zwischen den beiden Werten kann berechnet werden als
𝛥t= t1– t2 und daher 𝛥t= (𝜏1 ±e1)- (𝜏2 ±e2)
𝛥t= 𝜏1 – 𝜏2 + (e1 – e2) (2)
wobei (±e1)- (±e2) = ±σ (2a)
Wenn e₁ = e₂, was häufig bei Messdaten gleichen Ursprungs und gemessen mit dem gleichen Instrument der Fall sein kann, gilt ±σ = 0, d. h. ε₁ hebt ε₂ auf. Das bedeutet, dass die Anomalie
𝛥t= 𝜏1 – 𝜏2. (3)
die Differenz zwischen der jeweiligen Quantität ohne Fehler darstellt.
Um dieses Ergebnis zu erhalten, muss man jedoch sicher sein, dass der Fehler εx (genauer gesagt der systematische Fehler εx) in Größe und Richtung konstant bleibt. Dies ist sehr oft der Fall, wenn man die gleiche Größe mit dem gleichen Instrument in kurzen Zeitabständen misst. Die Gleichung (3) zeigt uns jedoch auch die Grenzen dieses Ansatzes auf. Was passiert, wenn ε₁ ≠ ε₂?
Noch interessanter ist die Frage, was passiert, wenn man Zeitreihen von Anomalien zeichnen muss, wenn e₁ ≠ e₂. Um dies zu veranschaulichen, werde ich das Verhalten von Anomalien in Zeitreihen für die Temperatur untersuchen, aber zuvor will ich uns eine der meist zitierten Studien der jüngeren Klimatologie genauer ansehen. B 06 stellte fest (S. 2 und 4):
(1) „Die Stationsnormale (Monatsdurchschnitte über den Normalzeitraum 1961–90) werden nach Möglichkeit aus den Stationsdaten für diesen Zeitraum generiert…. Die in einem Raster dargestellten Werte sind Anomalien, die durch Subtraktion der Stationsnormale von den beobachteten Temperaturen berechnet werden, sodass auch Fehler in den Stationsnormalen berücksichtigt werden müssen.“ In der folgenden Aussage wird dann eine Reihe von Fehlern definiert, und etwas später wird für einen bestimmten Fehlertyp (S. 6) Folgendes angegeben:
(2) „Es wird einen Unterschied zwischen der tatsächlichen mittleren Monatstemperatur (d. h. aus 1-Minuten-Durchschnittswerten) und dem von jeder Station aus weniger häufigen Messungen berechneten Durchschnitt geben; dieser Unterschied wird jedoch auch in der Stationsnormale vorhanden sein und sich in der Anomalie aufheben. Dies trägt also nicht zum Messfehler bei.“
Um zu überprüfen, ob dies zutrifft und was passieren könnte, und um die Auswirkungen von Fehlern in anomalen Zeitreihen weiter zu vereinfachen, verwende ich künstliche Sinuskurven anstelle von realen Temperaturdaten und belasten diese mit genau definierten systematischen Fehlern, die überall innerhalb des Zeitraums auftreten. Dazu wurde die Excel-Formel für einen Sinus mit einem zusätzlichen Mittelwert von 14,5 °C verwendet. Die Sinuskurve hat eine Amplitude von ± 0,25 °C mit einer Zykluszeit von etwa 70 Jahren. Abbildung 6 zeigt die ursprüngliche „Temperatur”-Zeitreihe mit einem leicht negativen Trend aufgrund der gewählten Start- und Endbedingungen, obwohl die Sinuskurve einen Trend von Null aufweist.
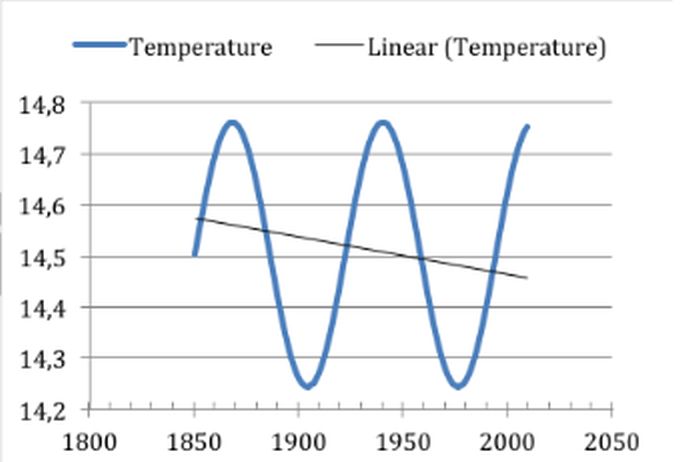
Abbildung 6 zeigt eine künstlich berechnete Zeitreihe der „globalen Durchschnittstemperatur” mit einer Amplitude von ± 0,25 °C und einem Zyklus von etwa 70 Jahren. Excel berechnet aufgrund der unausgeglichenen Zyklen korrekt einen negativen Trend, obwohl der Trend für eine vollständige Sinuswelle Null ist.
Auf diese Sinuswelle wurden zwischen 1860 und 2010, d. h. zwischen der Dauer der Beobachtungszeit, zwei verschiedene systematische Fehler überlagert. Die Ergebnisse sind in Abbildung 7 dargestellt.
Der erste angewendete Fehler war ein Sprung von + 1 °C, und das Ergebnis wird für verschiedene Zeitpunkte des Auftretens gezeigt. Die blaue Kurve zeigt die Anomalie (1) aus Abb. 2, noch ohne Fehler. Die rote Kurve (Anomalie 2) zeigt den Fehler, der 1940 auftrat, z. B. verursacht durch einen Umzug der Station an einen neuen Standort. Das könnte die Situation sein, die BO 06 im Sinn hatte, als sie davon ausgingen, dass sich der Fehler aufheben würde. Die grüne Kurve (Anomalie 2) zeigt den Fehler, der 1980 auftrat, d. h. innerhalb der Referenzzeit, und f. e. durch eine andere Lackierung der Station verursacht wurde, wie es in den USA geschehen ist, als alle Lackierungen bestehender Wetterhütten von Kalkfarbe auf Latexfarbe umgestellt worden sind. Dies wurde von Watts [11] in seinem umfassenden Bericht über die Qualität der Stationsdaten in den USA berichtet. Und die violette Kurve (Anomalie 4) zeigt die Auswirkungen eines „schleichenden” Fehlers von 0 bis 1 Grad über 100 Jahre, wie er durch den Einfluss des UHI (Urban Heat Island Effect) entstanden ist. Dies bezieht sich auf die langsamen Veränderungen der Umgebung durch die Errichtung von Parkplätzen, Gebäuden, Abfallverarbeitungsanlagen oder anderen vom Menschen verursachten Aktivitäten.
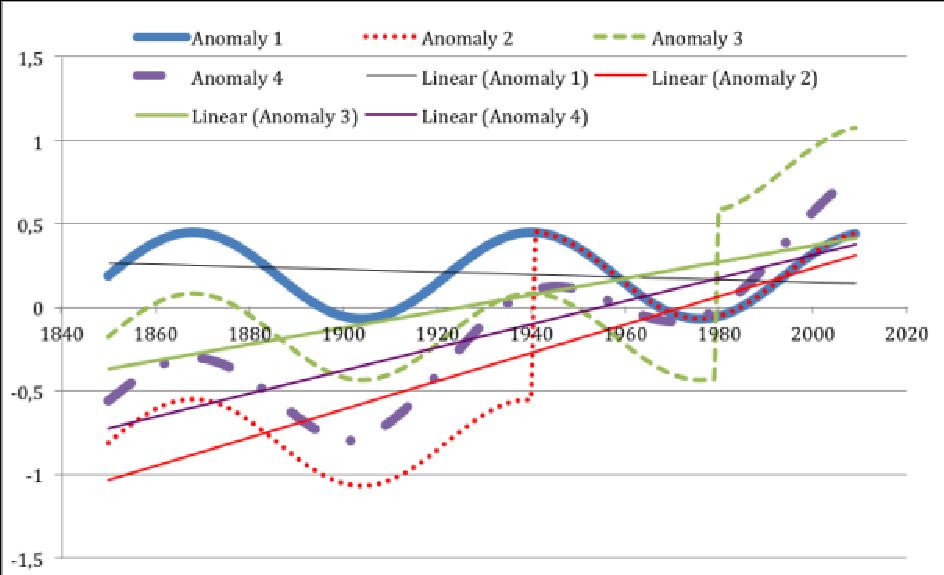
Abbildung 7: Blau (Anomalie 1) zeigt eine fehlerfreie, künstlich berechnete Zeitreihenanomalie einer „globalen Mitteltemperatur” mit einer Amplitude von ± 0,25 °C und einem Zyklus von etwa 70 Jahren. Der Referenzwert wurde anhand des Mittelwerts dieses Sinus‘ innerhalb des Zeitraums von 1961 bis 1990 berechnet. Darauf sind separat zwei verschiedene Fehler überlagert. Die rote Kurve (Anomalie 2) zeigt die Auswirkung eines systematischen Fehlers von 1 °C, der vor dem Referenzzeitraum von 1960 bis 1991 auftritt und seitdem kontinuierlich wirkt. Die grüne Kurve (Anomalie 3) zeigt den Einfluss eines systematischen Fehlers von 1 °C, der innerhalb des Referenzzeitraums von 1960 bis 1991 auftritt und seitdem kontinuierlich wirkt. Die violette Kurve (Anomalie 4) zeigt die Auswirkungen eines (linearen) „schleichenden” Fehlers von 0 bis 1 °C systematischem Fehler, der als UHI-Effekt auftreten kann, der langsam zunimmt, wenn immer mehr verschiedene Gebäude, Parkplätze und andere Einflüsse die Temperatur der lokalen Wetterstation beeinflussen. In jedem Fall sehe ich eine signifikante Veränderung des Trends (nur zwei dargestellt) und der Form der Anomalie-Zeitreihen, abhängig vom Ausgangspunkt des Fehlers und seiner Art. Es zeigt sich auch, dass sich Fehler nicht gegenseitig aufheben, unabhängig davon, wann sie auftreten, solange sie innerhalb des beobachteten Zeitraums auftreten.
Ich sehe in allen Fällen, dass der Fehler vollständig aktiv bleibt und sich im Verhältnis 1:1 auf die Zeitreihe des Anomaliewertes selbst auswirkt. Die Trendänderung ist ebenfalls in jedem Fall sichtbar. Es gibt nur eine Ausnahme: Wenn der Fehler vor Beginn des Untersuchungszeitraums auftritt, hebt er sich auf. Dies ist der einzige Fall, in dem die Anomalien die Fehler innerhalb der Daten aufheben.
In allen anderen Fällen heben Anomalien die Fehler ihrer Komponente nicht auf. Die Berechnung von Anomalien erfordert die Kombination der Unsicherheiten in der gemessenen Temperatur sowie der Unsicherheiten in der berechneten Durchschnittstemperatur, die sich aus dem Durchschnitt aller gemessenen Temperaturen innerhalb der Referenzzeit zusammensetzt. Dieses Hindernis wird oft nicht erwähnt. Denn die Anomalie selbst wird berechnet, indem von der absoluten monatlichen oder jährlichen lokalen Durchschnittstemperatur eine Referenz-Durchschnittstemperatur der gleichen Station abgezogen wird. Das heißt, jede lokale Durchschnittstemperatur ist ![]() ± ei , wobei „ei “ der Gesamtfehler in der i-ten gemittelten Temperatur
± ei , wobei „ei “ der Gesamtfehler in der i-ten gemittelten Temperatur ![]() ist.
ist.
Die Normaltemperatur ist ![]() , wobei
, wobei 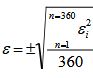 der durchschnittliche Fehler aus den dreißig Jahren gemessener Monatstemperaturen ist, die zu
der durchschnittliche Fehler aus den dreißig Jahren gemessener Monatstemperaturen ist, die zu ![]() gemittelt werden. Jede Anomalietemperatur ist
gemittelt werden. Jede Anomalietemperatur ist ![]() , und der Fehler in der Anomalie Δti kann in der Regel durch Anwendung der Formel für den Fehler in der Differenz zwischen zwei i-Messungen, dem quadratischen Mittelwert (r.m.s.) der Fehler in
, und der Fehler in der Anomalie Δti kann in der Regel durch Anwendung der Formel für den Fehler in der Differenz zwischen zwei i-Messungen, dem quadratischen Mittelwert (r.m.s.) der Fehler in ![]() Messungen, dem quadratischen Mittelwert (r.m.s.) der Fehler in f1 und T bestimmt werden, jedoch nur solange der Fehler als ziemlich normalverteilt angesehen werden kann. Dies ist nicht nur bei zufälligen Fehlern der Fall, sondern oft auch bei systematischen Fehlern. Sollte diese Bedingung jedoch nicht gegeben sein oder kann man sich nicht sicher genug sein, dann ist die einfache lineare Addition der genannten systematischen Fehler die richtige Vorgehensweise für die Fehlerfortpflanzung (siehe z. B. 1988; Miller S. 1353) [23] solcher Fehler.
Messungen, dem quadratischen Mittelwert (r.m.s.) der Fehler in f1 und T bestimmt werden, jedoch nur solange der Fehler als ziemlich normalverteilt angesehen werden kann. Dies ist nicht nur bei zufälligen Fehlern der Fall, sondern oft auch bei systematischen Fehlern. Sollte diese Bedingung jedoch nicht gegeben sein oder kann man sich nicht sicher genug sein, dann ist die einfache lineare Addition der genannten systematischen Fehler die richtige Vorgehensweise für die Fehlerfortpflanzung (siehe z. B. 1988; Miller S. 1353) [23] solcher Fehler.
Im ersten Fall ergibt sich der Fehler in Δti aus ![]() Er besteht also mindestens aus allen Fehlern seiner Komponenten.
Er besteht also mindestens aus allen Fehlern seiner Komponenten.
BO6 hatte einen solchen Fall erwähnt, da im gleichen Absatz geschrieben stand:
(3) „Wenn eine Station die Art und Weise ändert, wie die monatliche Durchschnittstemperatur berechnet wird, führt dies zu einer Inhomogenität in der Temperaturreihe der Station, und Unsicherheiten aufgrund solcher Änderungen werden Teil des Homogenisierungs-Anpassungsfehlers. (Hervorhebung durch den Autor)“.
Dass dies für alle Änderungen gilt, die während des Beobachtungszeitraums vorgenommen werden, haben die Autoren nicht erwähnt. Aber es ist so. Darüber hinaus wurden keine Angaben gemacht, um den erwarteten „Homogenisierungsprozess“ zu identifizieren, wie er durchgeführt wurde und wie erfolgreich er die Unsicherheiten beseitigt, mit Ausnahme der wenigen oben genannten. Es bleibt also eine Hoffnung, aber keine Tatsache. Dazu müssen die Unsicherheiten definiert und ihre Größe abgeschätzt werden. Dies werde ich als Nächstes tun.
Ergebnisse und Diskussion
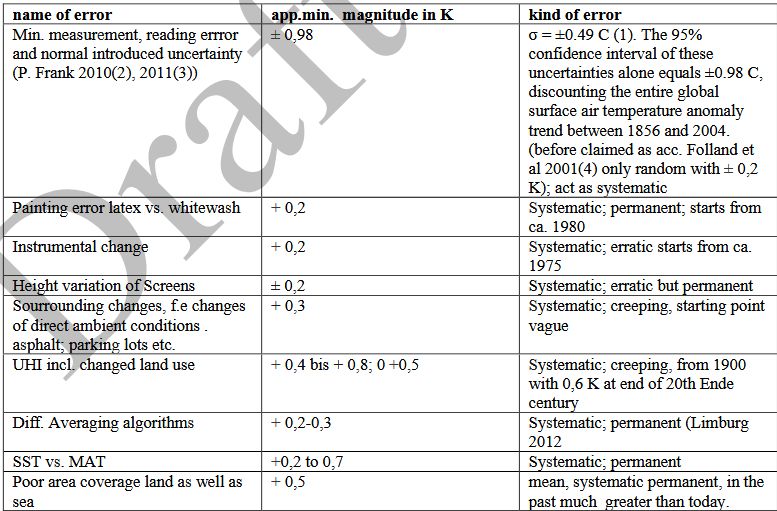
Aus früheren Arbeiten der Autoren wurde eine Reihe von Fehlern definiert, und es wurde ein sorgfältiger Versuch unternommen, diese sehr vorsichtig zu quantifizieren. Die folgende Tabelle zeigt die wichtigsten Fehler und deren wahrscheinliche Größenordnung sowie Richtung:
Es muss darauf hingewiesen werden, dass die meisten der oben genannten Fehler nur auf sorgfältigen Schätzungen beruhen. Dies gilt jedoch auch für alle Versuche, Fehler zu schätzen und zu korrigieren, die in der Literatur zu finden sind, soweit der Autor nach Durchsicht zahlreicher Literaturquellen weiß. Aus diesem Grund und aufgrund ihres hohen Ausmaßes ist der Autor der festen Überzeugung, dass die angegebenen Gesamtunsicherheiten eher konservativ als überschätzt sind.
Schlussfolgerungen
Der Hauptgrund für die Verwendung einer Anomalie liegt darin, dass die Abweichungen von der Durchschnittstemperatur in kohärenter Weise auftreten. So können Temperaturabweichungen von sehr vielen lokalen Durchschnittstemperaturen kombiniert werden, um die Trends des Klimawandels über ein großes Gebiet hinweg hervorzuheben.
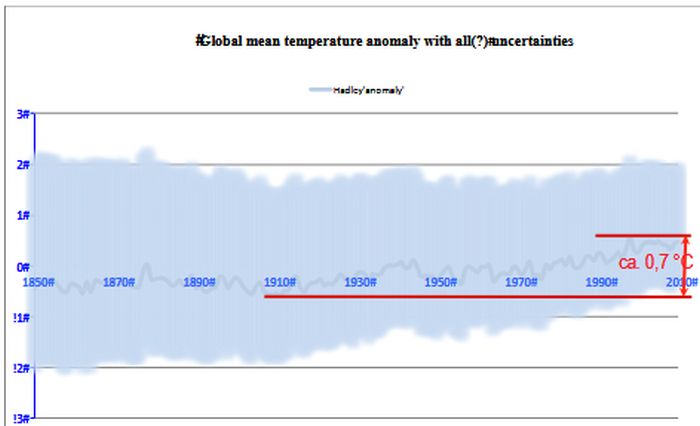
Abbildung 8: Geschätzte Unsicherheiten der Hauptfehlerklassen aus Tabelle 1 um eine beliebige Trendlinie. Die Basisdaten sind die gleichen wie in Abbildung 1. Die Unsicherheit ist jedoch deutlich größer als dort dargestellt. Da zudem nicht alle systematischen Fehler symmetrisch über die Zeit verlaufen, verläuft die Trendlinie nicht symmetrisch zu den Hüllkurvengrenzen. Da alle Fehler entweder zeitlich stabil sind oder langsam voranschreiten, sind Frequenzsignale die einzigen Signale, die präzise genug extrahiert werden können.
Anomalien werden berechnet, um die Nettotemperaturtrends der großen Vielfalt lokaler Klimazonen zu vergleichen oder zusammenzustellen. Der Preis für diesen Komfort besteht jedoch darin, dass die Anomalien, wie oben gezeigt, mit einer größeren Unsicherheit behaftet sind als die ursprünglichen Temperaturmessungen. Die einzige Ausnahme besteht darin, dass sich die Fehler aufgrund der Subtraktion von Daten verringern oder sogar aufheben können, wenn sie die gleiche Richtung und Größenordnung haben. Um dies zu erkennen, muss man diese Fehler jedoch im Voraus relativ genau bestimmen.
Man könnte argumentieren, dass der Mittelungsprozess selbst die Auswirkungen eines oder mehrerer Stationsfehler reduziert, unabhängig davon, ob dieser in den absoluten Daten oder in ihren Anomalien auftritt. Das ist richtig und einer der Vorteile der Mittelung. In der Meteorologie sind jedoch zahlreiche potenzielle Fehler bekannt, die an einer großen Anzahl von Stationen oder an allen Stationen nahezu gleichzeitig aufgetreten sind. Beispiele finden sich in der Literatur; ich nenne hier nur einige:
1. Änderung des Rasterdesigns, z. B. Wechsel vom hohen Wildtyp-Raster zum kleineren englischen Raster in Russland. Berichten zufolge geschah dies um 1914.
2. Einführung anderer Skalen von Réaumur (bis Ende des 19. Jahrhunderts auch in Deutschland) bis Celsius.
3. Einführung anderer Algorithmen zur Berechnung des Tagesmittelwerts. Dies geschieht sowohl in Europa als auch im Ausland sehr häufig.
Wie aus den USA, aber auch aus anderen Teilen der Welt berichtet wird, verschwindet der Wechsel der Lackierung von Tünche zu Latexweiß. Diese Liste lässt sich leicht erweitern.
Referenzen
[1] [1] P. Brohan, J. J. Kennedy, I. Harris, S. F. B. Tett, and P. D. . Jones “Uncertainty estimates in regional and global observed temperature changes: A new data set from 1850,” Journal of Geophysical Research, vol. 111, pp. 2006.
[2] P. Frank, “UNCERTAINTY IN THE GLOBAL AVERAGE SURFACE AIR TEMPERATURE INDEX: A REPRESENTATIVE LOWER LIMIT,” Energy & Environment, vol. 21 , no. 8, pp. 969–989, 2010.
[3] P. Frank, “IMPOSED AND NEGLECTED UNCERTAINTY IN THE GLOBAL AVERAGE SURFACE AIR TEMPERATURE INDEX,” Energy & Environment · , vol. Vol. 22, N, pp. 407–424, 2011.
[4] M. Anderson, “A Field Test of Thermometer Screens,” SHMI RMK, vol. 62, 1991.
[5] W. Köppen, “Einheitliche Thermometeraufstellungen für meteorologische Stationen zur Bestimmung der Lufttemperatur und der Luftfeuchtigkeit,” Meteorologische Zeitschrift, vol. 30, 1913.
[6] R. W. SPARKS, “THE EFFECT OF THERMOMETER SCREEN DESIGN ON THE OBSERVED TEMPERATURE,” vol. 315, 1972.
[7] P. van der M. Jitze, “A Thermometer Screen Intercomparison,” WMO Instruments and Observing Methods Reports , 1998.
[8] A. Sprung, “Bericht über vergleichende Beobachtungen verschiedenen Thermometer – Aufstellungen zu Gr. Lichterfelde bei Berlin,” Abhandlungen des Königlich Preussischen Meteorologischen Instituts. , vol. Bd. 1. No., 1890.
[9] VDI, “Uncertainties of measurement during acceptance tests on energy-conversion and power plants Fundamentals,” 2000.
[10] C. K. P. FOLLAND D. E., “Correction of instrumental biases in historical sea surface temperature data,” Q. J. R. Meteorol. Soc., vol. 121. , pp. pp. 319–367 , 1995.
[11] A. Watts, Is the U.S. Surface Temperature Record Reliable?, vol. 1. THE HEARTLAND INSTITUTE 19 South LaSalle Street #903 Chicago, Illinois 60603 www.heartland.org, 2009.
[12] J. R. Karl, T.R., Knight, R.W. & Christy, “Global and Hemispheric Temperature Trends: Uncertainties Related to Inadequate Spatial Sampling,” JOURNAL OF CLIMATE, vol. 7, p. 1144 bis 1163, 1994.
[13] P. D. G. Jones P. Ya Coughlan, M; , Plummer, M. C; Wang W-C, Karl, T.R, “Assessment of urbanization effects in time series of surface air temperature over land,” ature., vol. 347, p. 169 ff, 1990.
[14] P. D. N. Jones M; Parker, D. E. S.Martin, Rigor, I. G., “SURFACE AIR TEMPERATURE AND ITS CHANGES OVER THE PAST 150 YEARS,” Reviews of Geophysics, vol. 37, pp. 173–199, 1999.
[15] C. K. R. Folland N. A. Brown,S. J. Smith3, T. M. P. Shen, S. S. Parker1, D. E. and I. J. Macadam P. D. Jones, R. N. Nicholls, N. and Sexton, D. M. H., “Global temperature change and its uncertainties since 1861 ,” Hadcrut 2, HadCRUT2 error analysis , 2001.
[16] R. W. R. REYNOLDS SMITH, NICKA.STOKES, THOMASM. WANG, DIANEC. WANQIU, “An Improved In Situ and Satellite SST Analysis for Climate,” J O U R N A L O F C L I M A T E, vol. 15, pp. 1609–1625, 2002.
[17] R. W. Reynolds, “Sea Surface Temperature (SST) Analyses for Climate.” National Oceanic and Atmospheric Administration National Environmental Satellite, Data & Information Service National Climatic Data Center, 2002.
[18] G. Dietrich, “Über systematische Fehler in den beobachteten Wasser- und Lufttemperaturen auf dem Meere und über ihre Auswirkung auf die Bestimmung des Wärmeumsatzes zwischen Ozean und Atmosphäre,” Deutsche Hydrographische Zeitschrift, vol. 3 5/6, 1950.
[19] J. R. P. Christy David E. Brown,Simon Macadam, Ian Stendel,Martin and Norris, William B., “Differential Trends in Tropical Sea Surface and Atmospheric Temperatures Since 1979,” Geophysical Research Letters,, vol. 28, no.1 , pp. 183–186., 2001.
[20] E. C. K. A. and B. Kent David I., “Assessing Biases in Recent in situ SST andMarine Air Temperature,” 1998.
[21] C. Folland, “Assessing bias corrections in historical sea surface temperature using a climate model,” International Journal of Climatology, vol. 25, no. 7, pp. 895–911, 2005.
[22] E. R. Long, “CONTIGUOUS U. S. TEMPERATURE TRENDS USING NCDC RAW AND ADJUSTED DATA FOR ONE-PER-STATE RURAL AND URBAN STATION SETS,” SPPI ORIGINAL PAPER , 2010.
[23] J. C. M. and J. H. Miller, “Basic Statistical Methods for Analytical Chemistry Part I; Statistics of Repeated Measurements,” Analyst, vol. 113, pp. 1351–1356, 1988.
Eine pdf Version des Artikel (in englisch) kann hier heruntergeladen werden.historical temperature data - quality and treatment 1-Michaels iMac
Ein Vorläufer dieses Artikel erschien im Jahr 2014 im Energy & Environment hier