Korrelation von Sonnenstunden und Temperatur
von Dr. Konrad Voge
In diesem Artikel wird die Korrelation von Sonnenstunden und Lufttemperatur untersucht. In vielen Fällen der Untersuchung von Größen auf deren Zusammenhänge kann aus der Korrelation nicht auf die Kausalität geschlossen werden. In diesem Fall ist es umgekehrt. Die Kausalität dürfte unstrittig sein. Interessant ist jedoch die Stärke des Zusammenhangs. In einer 2024 veröffentlichten Arbeit wurde der Zusammenhang von Meeresströmungen (AMO-Atlantische Multidekaden Oszillation und NAO-Nordatlantische Oszillation) und der jährlichen Sonnenscheinstunden (SSH) dargestellt.
Daten
Grundlage der Auswertung sind die Zeitreihen des Deutschen Wetterdienstes (DWD) für die in 2 m Höhe über Grund gemessenen Temperaturen und die gemessenen Sonnenstunden. Es wurden die Zeitreihen aller Meßstationen des DWD auf brauchbare Datensätze geprüft. Ein „brauchbarer“ Datensatz liegt dann vor, wenn „genügend“ Werte sowohl von der Temperatur als auch von Sonnenstunden vorliegen. Es müssen also in einem Jahr beide Werte gemessen worden sein. Auf die Qualität der Meßwerte soll hier nicht weiter eingegangen werden. Dem Autor ist klar, dass die Werte hohen Qualitätsansprüchen nicht genügen. Da jedoch keine anderen Datensätze in dem Umfang vorhanden sind, kann man entweder nichts machen oder hoffen, dass die große Anzahl von Werten die Fehler etwas mildert.
| Bundesland | Anzahl
Meßstationen |
Anzahl
Meßwerte |
| Baden-Württemberg | 46 | 2205 |
| Bayern | 58 | 3239 |
| Berlin | 6 | 283 |
| Brandenburg | 17 | 861 |
| Bremen-Hamburg | 7 | 352 |
| Hessen | 20 | 1060 |
| Mecklenburg-Vorpommern | 17 | 845 |
| Niedersachsen | 33 | 1639 |
| Nordrhein-Westfalen | 37 | 1609 |
| Rheinland-Pfalz | 21 | 1020 |
| Saarland | 5 | 239 |
| Sachsen | 21 | 950 |
| Sachsen-Anhalt | 12 | 859 |
| Schleswig-Holstein | 31 | 1215 |
| Thüringen | 18 | 822 |
| Summe | 349 | 17198 |
Tabelle 1 Anzahl der ausgewerteten Meßstationen und Meßwerte
In die Auswertung sind die Zeitreihen von 349 Meßstationen aufgenommen worden. Wie diese sich auf die Bundesländer verteilen, ist in Tabelle 1 zusammengestellt. Die Verteilung der hier betrachteten Meßstationen über Deutschland zeigen die Bilder 1 bis 3. In diesen Bildern sind die Verteilungen nach der Höhe über Meeresspiegel (Höhe), Geographischer Breite (Breite) und Geographischer Länge (Länge) abgebildet.
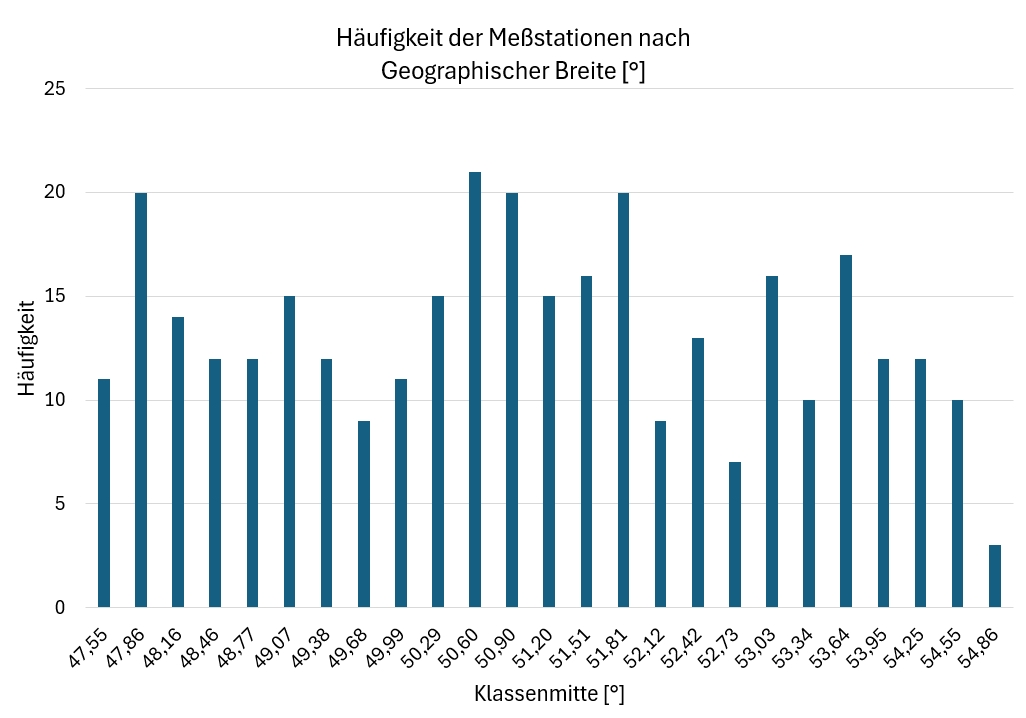
Bild 1 Verteilung der Meßstationen nach der geographischen Breite
Aus der Verteilung geht hervor, dass über der geographischen Breite die Meßstationen annähernd gleichmäßig verteilt sind. Anders die Verteilung der Meßstationen bezüglich der geographischen Länge nach Bild 2. Während die Verteilung über der Breite einigermaßen gleichmäßig ist, konzentrieren sich die Meßstationen bezüglich der Länge auf die Mitte Deutschlands. Die Verteilung nach der Höhe in Bild 3 zeigt eine starke Konzentration auf die Klasse 0…118 m (Klassenmitte 59 m).

Bild 2 Verteilung der Meßstationen nach der geographischen Breite

Bild 3 Verteilung der Meßstationen nach der Höhe über Meeresspiegel
Auswertung
Wie oben erwähnt, wird der statistische Zusammenhang des Einflusses der Anzahl der jährlichen Sonnenstunden auf die jährliche mittlere Temperatur gesucht. Da die Anzahl der Sonnenstunden und die Temperatur Zufallsvariablen sind, liegt Modell II der Statistik vor und es kann ein Korrelationskoeffizient berechnet werden. Es sind für alle hier betrachteten 349 Meßstationen Regressionsgeraden und die Korrelationsfaktoren berechnet. Als Beispiel ist in Bild 4 die Regressionsgerade der Meßstation Hohenpeißenberg (die gern als Beispiel verwendet wird) dargestellt. Der zugehörige Korrelationskoeffizient r = 0,57.
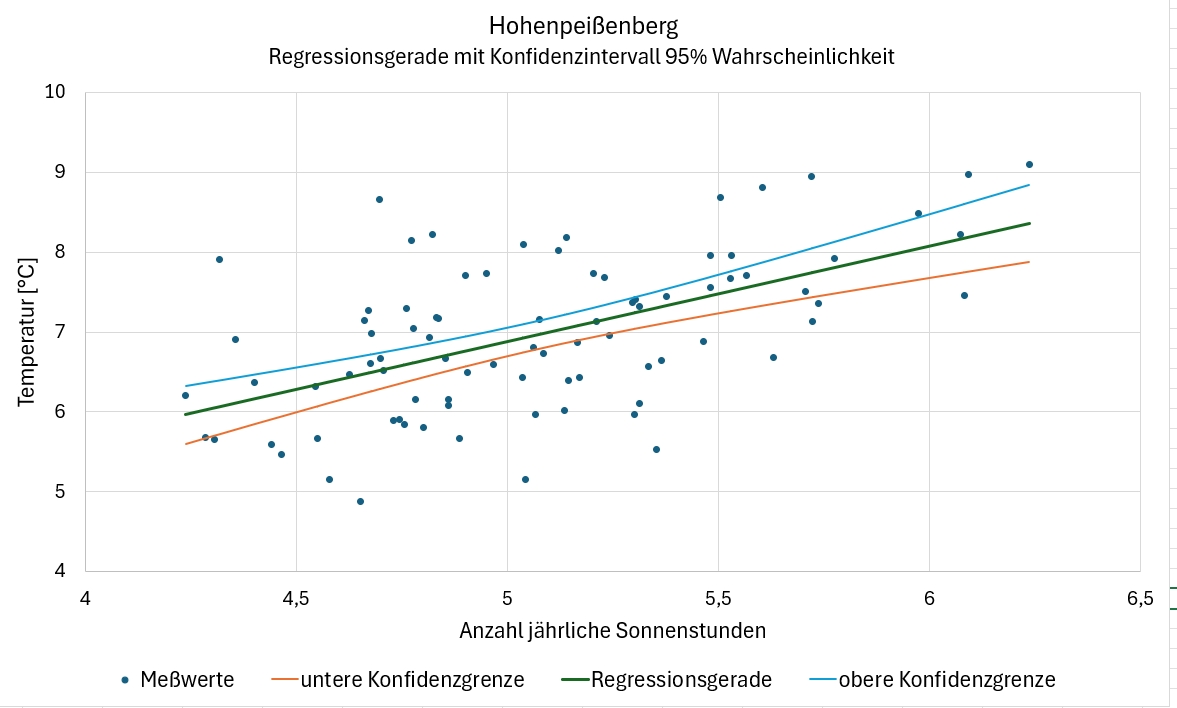
Bild 4 Zusammenhang Sonnenstunden und Temperatur an der Station Hohenpeissenberg gemessen. Die Meßreihe beginnt 1937 und umfasst 85 Wertepaare.
Die Spanne der Korrelationskoeffizienten ist mit -0,22 < r < 0,88 relativ groß. Auffallend sind die Meßstationen Fulda-Horas (Hessen) und Karlshuld (Bayern), bei denen negative Korrelationskoeffizienten berechnet wurden. Dies erscheint aufgrund der Kausalität nicht möglich. Es setzte voraus, dass immer kalte Luftströmungen den Einfluss der Sonne aufheben würden. Vermutlich zeigt es jedoch die Unzuverlässigkeit der Daten. Diese beiden Meßstationen sind aus den weiteren Betrachtungen herausgenommen.
Die Klassierung der Korrelationskoeffizienten in 25 Klassen zeigt Bild 5. In diesem Bild ist eine Normalverteilung mit dargestellt. Obwohl dem Bild nach eine Normalverteilung vermutet werden könnte, wird mit dem Shapiro-Wilk Test die Nullhypothese abgelehnt.
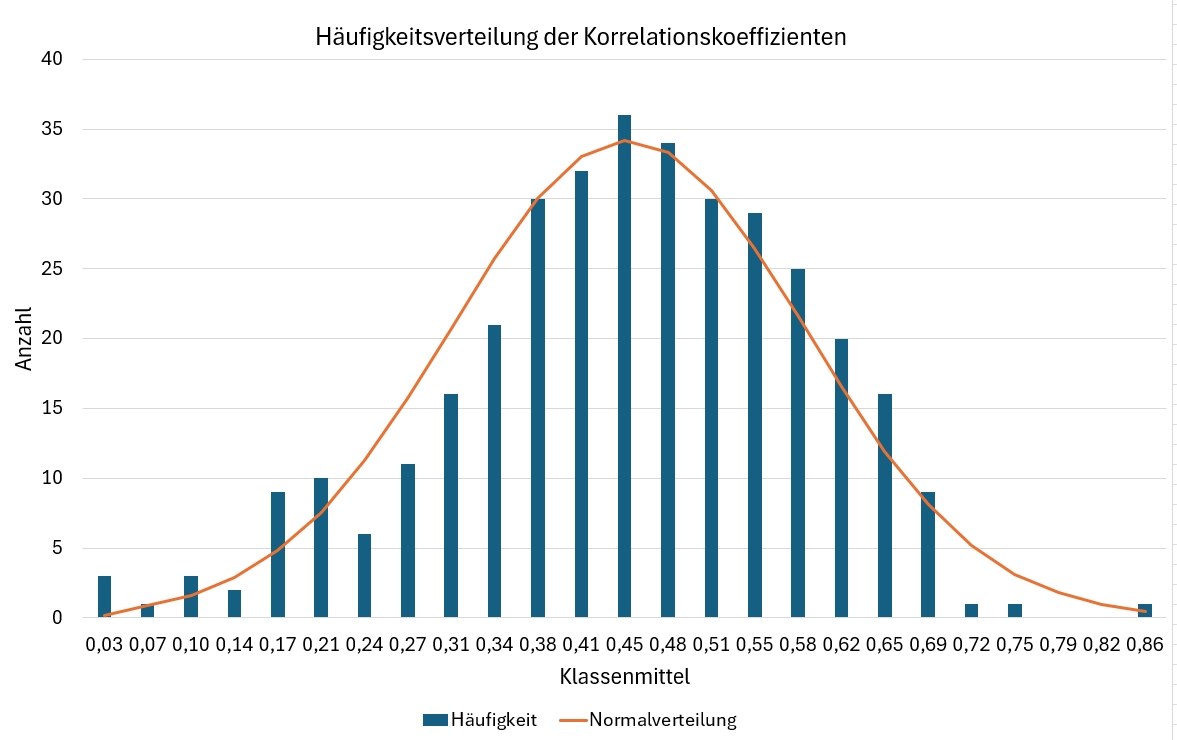
Bild 5 Verteilung der Korrelationskoeffizienten
Erwartungswert 0,45
Standardabweichung 0,14
Einflussfaktoren
In den Bildern 1 bis 3 ist die Verteilung der hier untersuchten Meßstationen gezeigt. Demnach können Länge, Breite und Höhe einen Einfluss auf Sonnenstunden und Temperatur ausüben, was sich dann in den Korrelationskoeffizienten ausdrückt. Es ist demnach eine Funktion
f(x1, x2, x3)
zu bestimmen, wobei x1-Breite, x2-Länge und x3-Höhe bedeuten. Mittels Ausgleichsrechnung nach dem Verfahren der Minimierung der Summe der Fehlerquadrate werden die Koeffizienten a0…a123 bestimmt. Die Funktion hat folgende Form:
f(x1, x2, x3) = a0+ a1 x1+ a2 x2+ a3 x3+ a12 x1 x2+ a13 x1 x3+ a23 x2 x3+ a123 x1 x2 x3
Es wird ein linearer Einfluss der Variablen sowie deren Wechselwirkungen angesetzt. Die Funktion f(x1, x2, x3) stellt ein dreidimensionales Gebilde in Form eines „Ausgleichskörpers“ dar. Tabelle 2 enthält die Werte der Koeffizienten a0…a123.
| Koeffizient | |
| a0 | 1,64912917 |
| a1 | 0,02543109 |
| a2 | -9,74E-02 |
| a3 | -1,29E-02 |
| a12 | 2,08E-03 |
| a13 | 0,00026335 |
| a23 | 0,00103926 |
| a123 | -2,11E-05 |
Tabelle 2 Koeffizienten der Ausgleichsfunktion
In Bild 6 sind Einfluss von Länge und Breite auf die Korrelationskoeffizienten bei einer Höhe von 300 m zu sehen. Es lässt sich, da drei unabhängige Variable (x1, x2, x3) und eine abhängige Variable (r) vorliegen, nur eine Fläche bei einer festen Variablen (hier x3) darstellen.
In den Bildern 7 bis 9 sind zur weiteren Verdeutlichung zwei unabhängige Variablen festgehalten, um so den Einfluss einer Größe darstellen zu können.
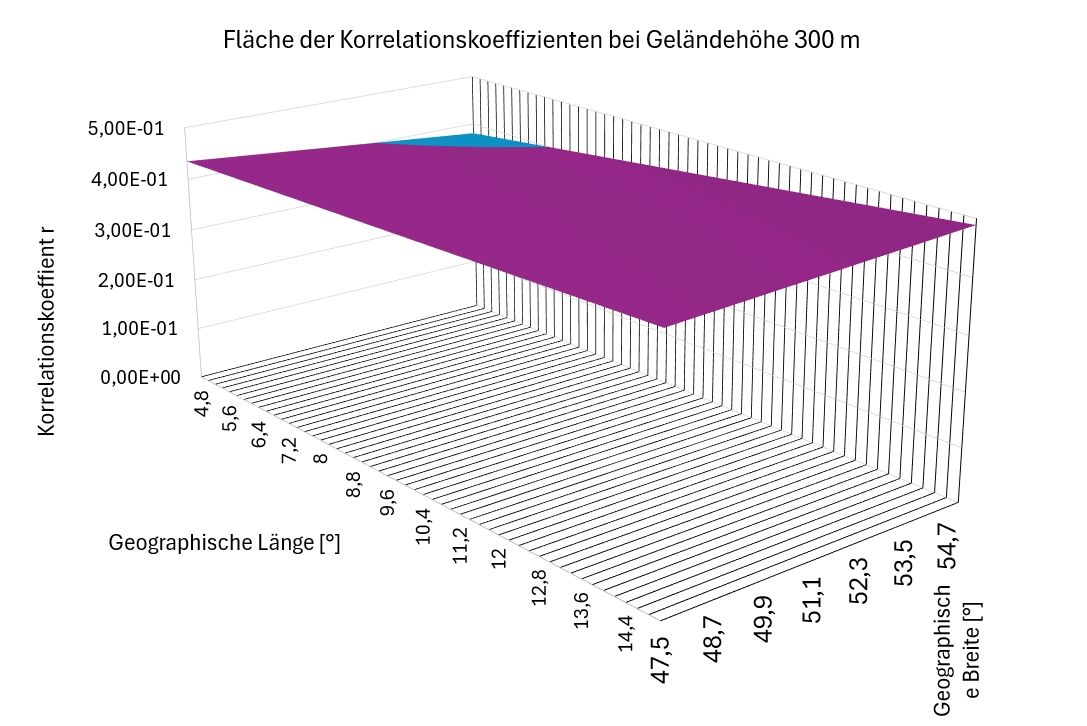
Bild 6 Einfluss von Länge und Breite auf die Korrelationskoeffizienten bei einer Höhe von 300 m
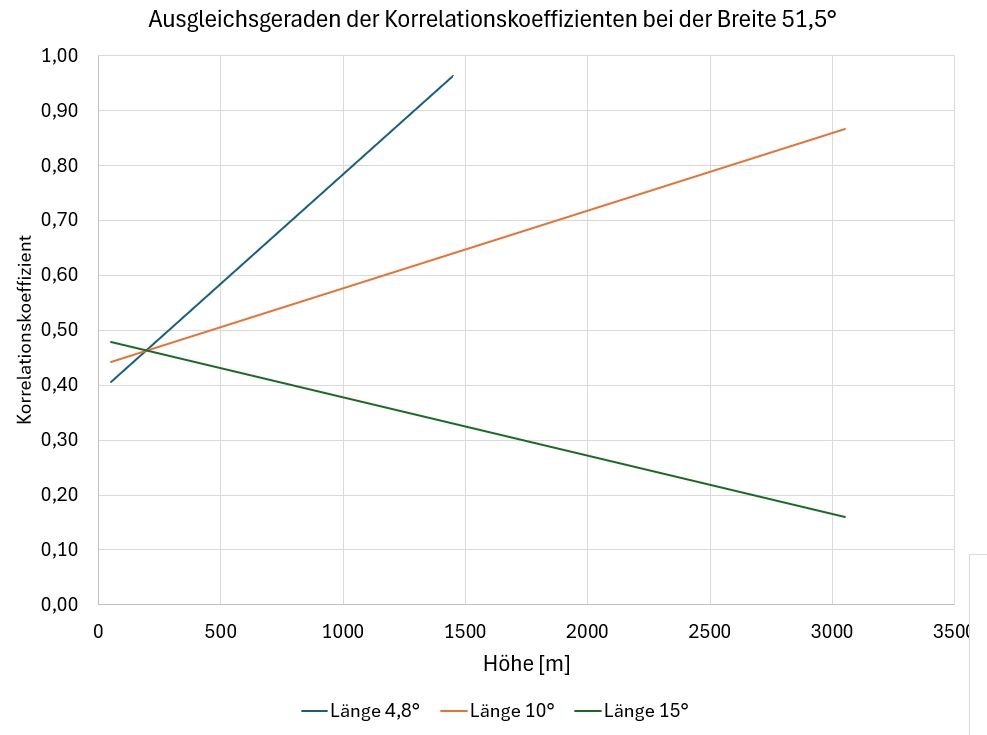
Bild 7 Einfluss der geographischen Länge und der Höhe über NN bei einer geographischen Breite von 51,5 °
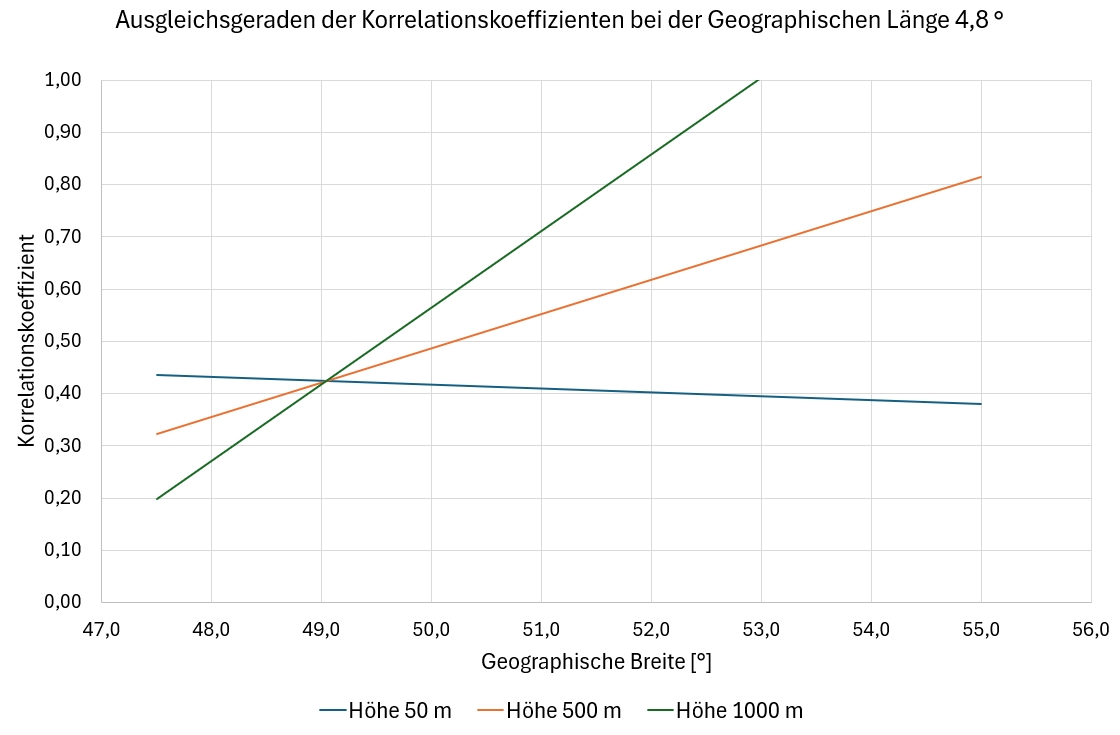
Bild 8 Einfluss der geographischen Breite und der Höhe über NN bei einer geographischen Länge von 4,8 °
Die Geraden in den Bildern 7 bis 9 sind mit der Ausgleichsfunkton und den Koeffizienten aus Tabelle 2 berechnet. Es ist zu sehen, dass die geographische Breite und die Höhe über Meeresspiegel einen starken Einfluss auf den Korrelationskoeffizient ausüben, da eine starke Spreizung der Geraden vorliegt. Die geographische Länge hat einen geringeren Einfluss auf die Korrelationskoeffizienten, wie Bild 9 zeigt. Es sind hier aus der Vielzahl der möglichen Kombinationen einige Beispiele herausgegriffen, um Tendenzen zu zeigen.
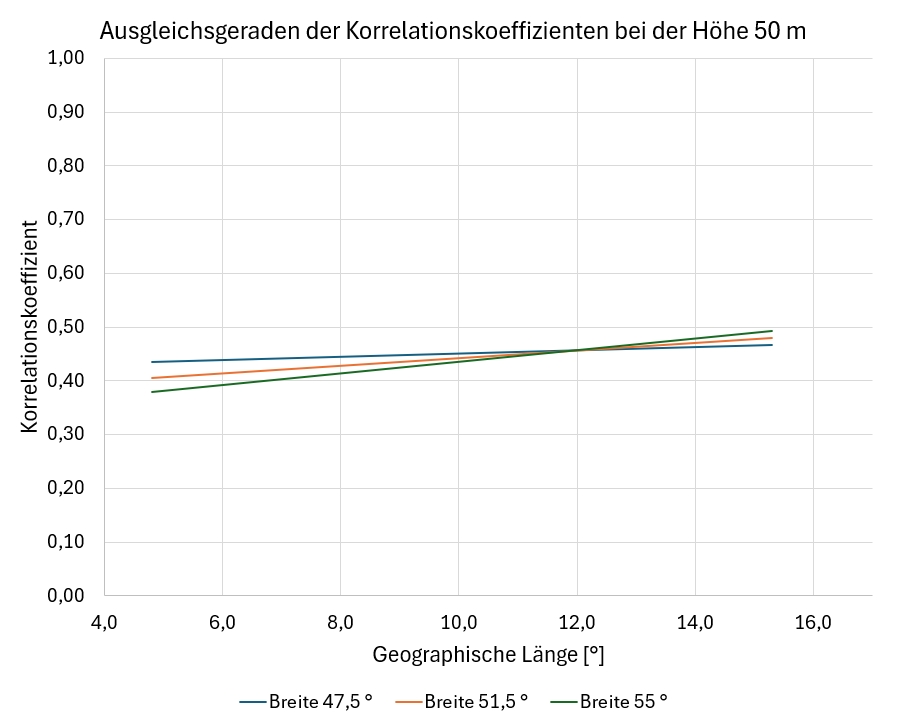
Bild 9 Einfluss der geographischen Länge und Breite bei einer Höhe von 50 m über NN
Zusammenfassung
Für die Zeitreihen von 349 Meßstationen bezüglich Anzahl der gemessenen Sonnenstunden und der Temperatur wurden Regressionsfunktionen und die sich daraus ergebenden Korrelationskoeffizienten bestimmt. Es wurden nur diejenigen Jahre der Zeitreihen verwendet, wo Anzahl der Sonnenstunden und Temperatur gemessen wurden. Die Auswertung hat ergeben, das die Spanne der Korrelationskoeffizienten -0,22 < r < 0,88 beträgt und damit relativ groß ist. Die zwei berechneten negativen Korrelationskoeffizienten wurden aus der Auswertung herausgenommen, da sie nicht plausibel sind.
Weiterer Artikel
Horst-Joachim Lüdecke, Gisela-Müller Plath und Sebastian Lüning
https://eike-klima-energie.eu/2024/11/15/die-sonnenscheindauer-europas-im-tanz-der-wolken/