Die spektrale Problematik einer terrestrischen Stefan-Boltzmann-Inversion [Teil 2]

Uli Weber

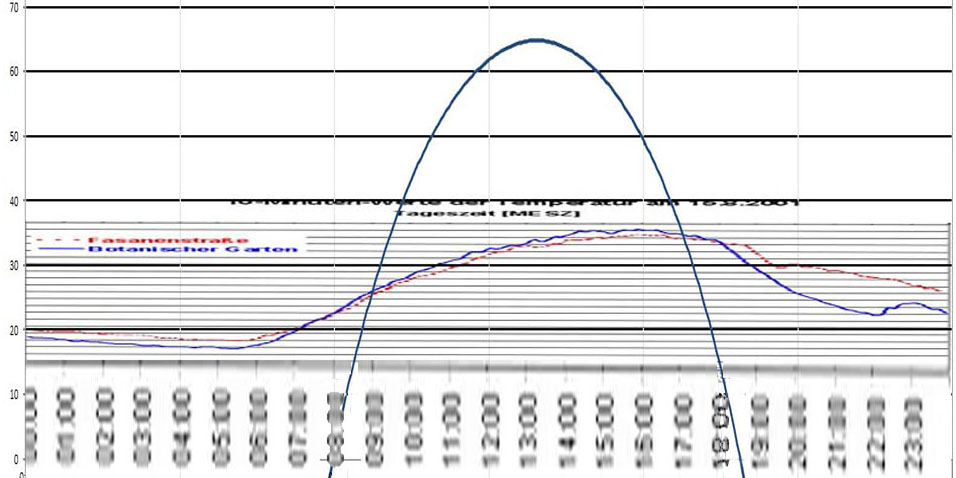Im ersten Teil hatten wir beim Vergleich der am 15. August 2001 in Berlin gemessenen Temperatur und dem berechneten S-B-Temperaturäquivalent von Berlin festgestellt, dass offenbar die solare HF-Einstrahlung bereits erwärmt, bevor das rechnerische S-B-Temperaturäquivalent aus der terrestrischen S-B-Inversion die morgendliche Ortstemperatur überschreitet.

Abbildung 1: Direkter Vergleich der gemessenen 10-Minuten-Werte der Temperatur in Berlin am 15. August 2001 (FU Berlin) mit dem S-B-Temperaturäquivalent für Berlin am selben Tag mit Albedo

Copyright Freie Universität Berlin, 14195 Berlin – Alle Rechte vorbehalten: „Wir erlauben ausdrücklich und begrüßen das Zitieren unserer Dokumente und Webseiten sowie das Setzen von Links auf unsere Website.“

Das daraus abgeleitete vorläufige Ergebnis bestand aus den folgenden Möglichkeiten:

1. Der beschriebene frühzeitige Temperaturanstieg ist ein Artefakt und kann getrost ignoriert werden.
2. Eine terrestrische Stefan-Boltzmann-Inversion kann nach Argument [7] das solare HF-Spektrum nicht korrekt abbilden.
3. Zwar ist das maximale S-B-Temperaturäquivalent einer terrestrischen S-B-Inversion des einfallenden solaren HF-Spektrums nach Argument [10] auf den Betrag der spezifischen Strahlungsleistung beschränkt, aber insgesamt steigt die Temperaturkurve steiler an und das Maximum wird breiter, als es das Stefan-Boltzmann-Gesetz vorgibt

So, und um sich jetzt einem der möglichen Ergebnisse anzunähern, schauen wir uns mal die Messungen vom Hamburger Wettermast vom 5. bis 12. Juni 2024 an. Nachfolgend zunächst einmal die entsprechenden solaren Daten für Hamburg am 08. Juni 2024, und danach die Wetterdaten vom Hamburger Wettermast:

Solar Noon 13:19 MESZ

Erhebung Sonne 59 Grad

Mittagsrichtung 180 Grad

Sonnenaufgang 04:52 MESZ

Sonnenuntergang 21:46 MESZ

Tageslänge 16:54:16 Stunden

Abbildungen 2 A-D: Wetterdaten vom Hamburger Wettermast für die Zeit 5.6. bis 12.6.2024:

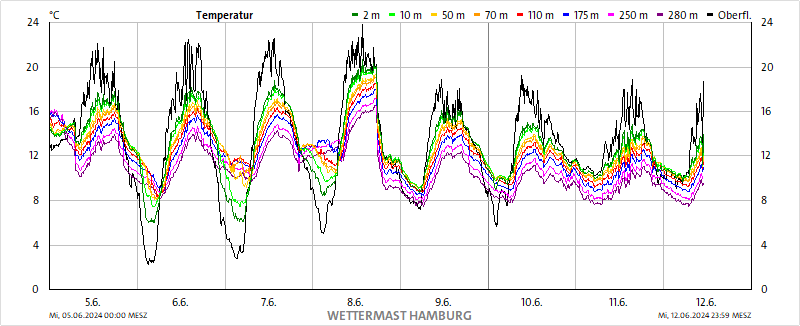
Abbildung 2A: Temperaturverlauf 5.6. bis 12.6.2024 vom Wettermast HH

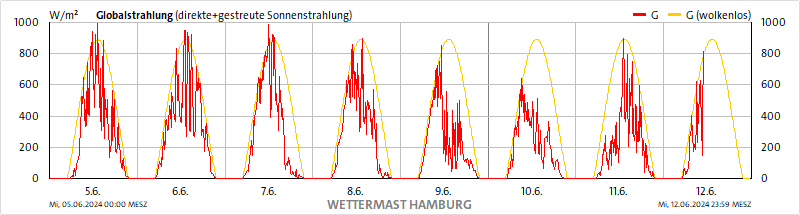
Abbildung 2B: Globalstrahlung 5.6. bis 12.6.2024 vom Wettermast HH

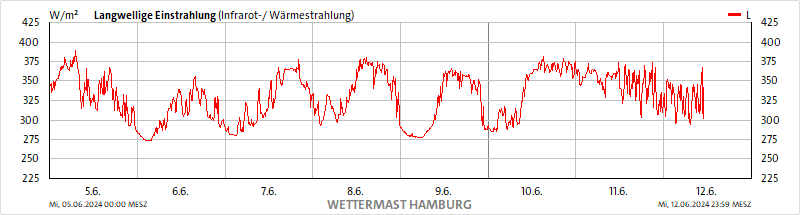
Abbildung 2C: Langwellige Einstrahlung 5.6. bis 12.6.2024 vom Wettermast HH

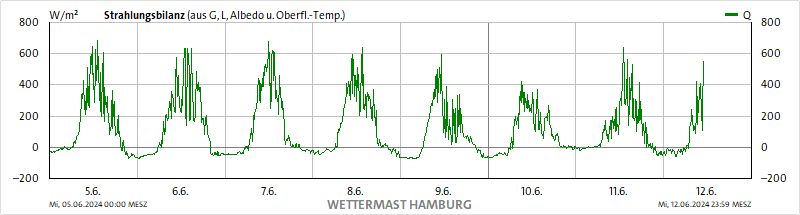
Abbildung 2D: Strahlungsbilanz 5.6. bis 12.6.2024 vom Wettermast HH

Dortige Anmerkung zur Strahlungsbilanz: „Die Strahlungsbilanz wird berechnet aus der Globalstrahlung, der langwelligen Einstrahlung, einer konstanten Albedo von 0,21, der Erdbodenoberflächentemperatur und einer konstanten langwelligen Emissivität des Erdbodens von 0,984. Diese Bilanz stimmt recht genau für eine grüne Wiese, insbesondere aber nicht für eine geschlossene Schneedecke!“

Der morgendliche Temperaturanstieg in Abbildung 2A erfolgt am 6. bis 8. und 10. Juni deutlich früher als der Sonnenaufgang, während die Globalstrahlung in Abbildung 2B an allen diesen Tagen dem Sonnenauf- und -untergang exakt folgt. Die langwellige Einstrahlung in Abbildung 2C sinkt von einem Tagesmaximum um den Mittag kontinuierlich auf ihr Minimum zum Beginn des Folgetages ab, während die Strahlungsbilanz in Abbildung 2D bereits vor Sonnenuntergang auf ihr Minimum zurückfällt, das es am Folgetag erst nach Sonnenaufgang wieder verlässt.

In den nachfolgenden Abbildungen 3 A-D wurden die Wetterdaten aus Abbildung 2 A-D für den 08.06.2024 grafisch auf eine 24h-Skala gestreckt:

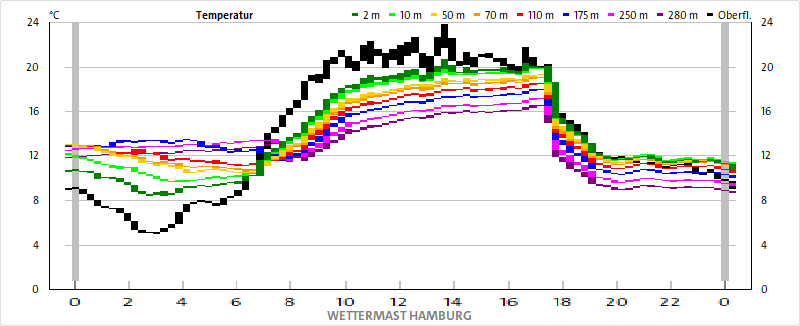Abbildung 3A: Temperaturverlauf am 08.06.2024 vom Wettermast HH

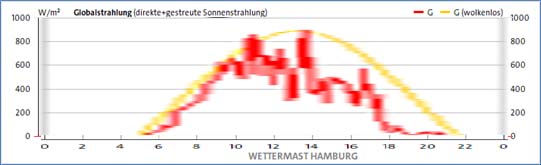
Abbildung 3B: Globalstrahlung am 08.06.2024 vom Wettermast HH

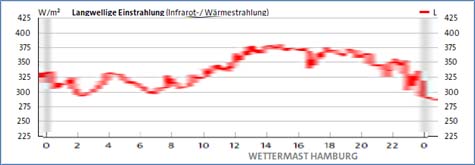
Abbildung 3C: Langwellige Einstrahlung am 08.06.2024 vom Wettermast HH

 

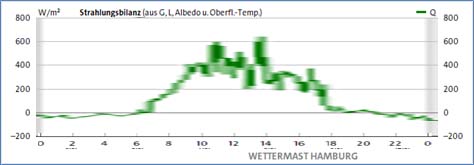
Abbildung 3D: Strahlungsbilanz am 08.06.2024 vom Wettermast HH

Der Temperaturanstieg in Abbildung 3A beginnt bereits etwa zwei Stunden vor Sonnenaufgang. Dieser Verlauf wird durch die 24h-Kurven vom 6., 7. und 10. Juni in Abbildung 2A gestützt. Sehr gut ist hier die Umkehr des Temperatur-Höhenprofils zu erkennen. In den Morgenstunden ist die Bodentemperatur noch am niedrigsten, während die Temperatur mit der Höhe zunimmt. Nach Sonnenaufgang kommt es gegen 7:00 Uhr dann zunehmend zu einer Umkehr dieses Profils, sodass die Bodentemperatur die höchsten Werte aufweist und nach oben hin abnimmt, bis es gegen 18:00 Uhr zu einem abrupten Temperaturabfall kommt. An der Aussage zur Globalstrahlung in Abbildung 3B ändert sich nichts, sie folgt exakt dem Sonnenauf- und –untergang. Die langwellige Einstrahlung in Abbildung 3C hat ihr Tagesmaximum zwischen Mittag und Mitternacht, bleibt aber über den in Abbildung 2C dargestellten Zeitraum nicht einheitlich genug für eine generelle Aussage.

In der Beschreibung „Daten vom Wettermast Hamburg“ wird unter A.11.3. die Strahlungsbilanz (lang- und kurzwellig) als die Nettostrahlungsflussdichte

Q = G − R + L – E mit kurzwelliger Strahlung von oben G, kurzwelliger Strahlung von unten R, langwelliger Strahlung von oben L und langwelliger Strahlung von unten E definiert.

Bei abwärts gerichtetem Nettostrahlungsfluss ist die Strahlungsbilanz positiv. In Abbildung 3D ist die Strahlungsbilanz also zwischen etwa 7:00 Uhr und 18:00 Uhr positiv, die negativen Beträge zwischen 0:00 Uhr und 7:00 Uhr sowie zwischen 18:00 Uhr und 24:00 Uhr wiegen diese positive Bilanz nicht auf, sodass die Strahlungsbilanz über den gesamten Zeitraum vom 5.6. bis 12.6.2024 insgesamt positiv bleibt. Die Daten vom Wettermast Hamburg können die Problematik der eingangs aufgezeigten Fälle [I], [II] und/oder [III] für eine S-B-Inversion des solaren Spektrums leider auch nicht vollständig auflösen, weil hier der gemessene Tempertaturanstieg (Abbildungen 2&3 A) sogar schon deutlich vor dem Sonnenaufgang beginnt. Eine rein aus den Meßwerten abgeleitete eindeutige Auflösung aller Fragestellungen [I], [II] und/oder [III] ist daher unmöglich geworden.

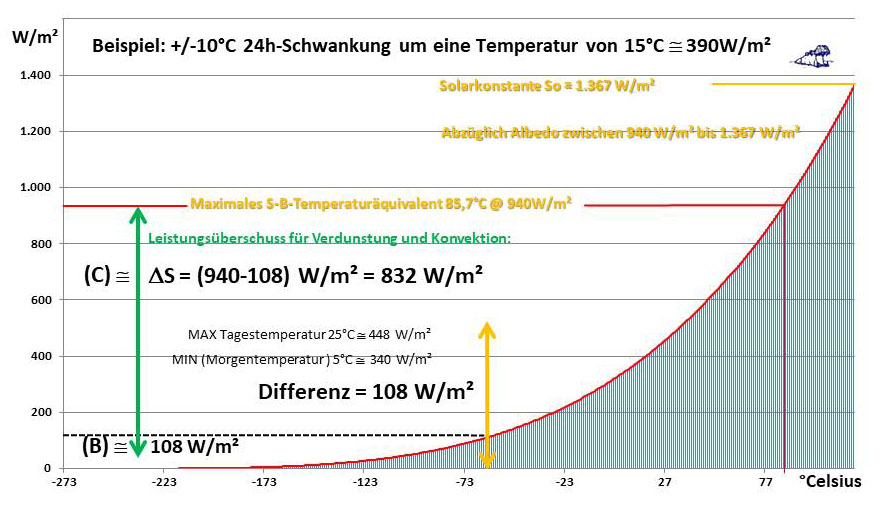Eindeutig geklärt ist lediglich, dass das solare Temperaturäquivalent aus der S-B-Inversion nicht erst über die Ortstemperatur ansteigen muss, um dort einen Temperaturanstieg zu verursachen; damit kann der Fall [I] ausgeschlossen werden, dieser Effekt ist also kein Artefakt:

Abbildung 4: Korrektur für die Beziehung zwischen Temperatur und spezifischer solarer Strahlungsleistung im Stefan-Boltzmann-Gesetz am Beispiel des Leistungsbedarfs einer Oberflächentemperatur von 15°C +/-10°C

Das bedeutet für die Beziehung zwischen Temperatur und der terrestrischen S-B-Inversion des solaren HF-Strahlungsspektrums:

Der Temperaturbereich (A) aus der ursprünglichen Abbildung 1 in Teil 1 mit einer solaren Einstrahlung ohne einen örtlichen Temperaturanstieg bis zum S-B-Strahlungsäquivalent der Ortstemperatur entfällt.

Der Temperaturbereich (B) erhöht ab Sonnenaufgang sofort die Ortstemperatur vom morgendlichen Minimum und dann im weiteren Tagesverlauf bis zum Tagesmaximum am Nachmittag, während gleichzeitig

der Temperaturbereich (C) durch Verdunstung und Konvektion aus der solaren Einstrahlung „abgeschöpft“ wird. Es wird hieraus also unmittelbar deutlich, dass die Energie in den globalen Zirkulationen von Atmosphäre und Ozeanen auf der Tagseite der Erde zusammen mit der örtlichen Temperaturgenese „wieder aufgeladen“ wird.

Die Bereiche (B) und (C) folgen also nicht streng aufeinander, sondern sie überschneiden sich und lassen sich daher auch nicht eindeutig voneinander trennen. Vielmehr flacht der Temperaturanstieg bei steigender solarer Einstrahlung zum Mittag hin zwar deutlich ab, eine Umkehr zu fallenden Temperaturen findet aber erst am späten Nachmittag statt.

Im Ergebnis dürfte das solare HF-Spektrum die Flankensteilheit der S-B-T⁴-Kurve übersteigen, ohne über das maximale S-B-Temperaturäquivalent der Solarkonstanten hinauszugehen.

Aus den Abbildungen 2&3 B-D wird deutlich, dass die gemessene und berechnete Globalstrahlung (Abb. 2&3 B) korrekt auf den Zeitraum zwischen Sonnenauf- und –untergang beschränkt sind. Die Dia­gramme der langwelligen Einstrahlung (Abb. 2&3 C) sehen insgesamt sehr heterogenen aus und zeigen oft ein Maximum zwischen Mittag und Mitternacht. Die Strahlungsbilanz als positive Nettostrahlungs­flussdichte (Abb. 2&3 D) schließlich beschränkt sich auf einen Zeitraum zwischen etwa 7:00 und 18:00 Uhr. Insbesondere ist zum nachfolgenden Tag keinerlei Summationseffekt erkennbar, die Bilanz sinkt vielmehr zum Abend hin wieder deutlich ab. Es handelt sich damit just um den Zeitraum, in dem sich das Tempe­ratur-Höhenprofil (Abb. 3A) von Nacht zu Tag umkehrt. Dabei dürfte es sich genau um denjenigen Zeitbereich der solaren Einstrahlung handeln, in dem die Oberflächentemperatur einen konvektiven Wärmetrans­port anzutreiben vermag. Wenn wir also das positive Ungleichgewicht der Strahlungs­bilanz am hellen Tag als konvektive Ableitung von Wärme verstehen, dann bleibt für die örtliche Bilanz lediglich eine geringe Schwankung um die 0-Linie übrig. Und das reicht für eine sogenannte „atmosphärische Gegenstrahlung“ von 155W/m² netto auf gar keinen Fall aus. Nach dem THE-Paradigma soll diese „Gegenstrahlung“ einen Temperaturanstieg der Ortstemperatur von 33° verur­sachen, ist aber, insbe­sondere nachts, in der Strahlungsbilanz vom Wettermast HH überhaupt nicht enthalten und bestätigt damit implizit genau mein hemisphärisches Stefan-Boltzmann-Modell.

Eine vollständige Lösung für die Fälle [II] und/oder [III] bleibt eine finale Auf­gabe für die Experimentalphysik.