Die spektrale Problematik einer terrestrischen Stefan-Boltzmann-Inversion [Teil 1]

geschrieben von Admin | 9. Juli 2024

Uli Weber

https://eike-klima-energie.eu/wp-content/uploads/2023/08/word-image-106414-6.jpeg Sie erinnern sich vielleicht noch ein meinen vorletzten EIKE-Artikel? Für eine Temperaturberechnung aus der solaren Einstrahlung mit dem Stefan-Boltzmann-Gesetz ist generell eine terrestrische S-B-Inversion nötig. Im Ergebnis hatte ich dort dann drei unterschiedliche Leistungsbereiche für die terrestrische Temperaturgenese definiert:

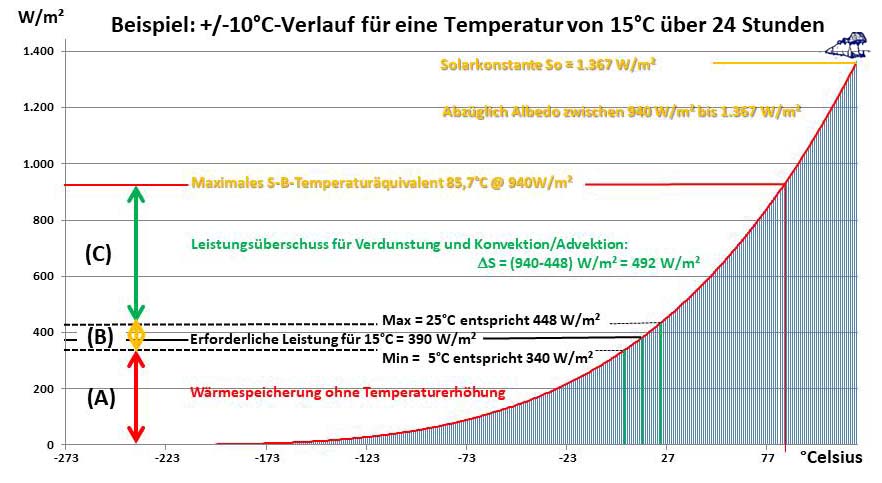
Abbildung 1: Die Beziehung zwischen Temperatur und spezifischer Strahlungsleistung im Stefan-Boltzmann-Gesetz am Beispiel des Leistungsbedarfs einer Oberflächentemperatur von 15°C +/-10°C

Der Temperaturbereich (A) der solaren Einstrahlung liegt unter dem S-B-Strahlungsäquivalent der dargestellten Minimumtemperatur und trägt daher nicht zur Temperatur bei, sondern erhöht lediglich den Energieinhalt.

Der Temperaturbereich (B) erhöht dann die Temperatur vom Minimum aufs Maximum, während gleichzeitig

der Temperaturbereich (C) durch Verdunstung sowie Konvektion/Advektion aus der Einstrahlung „abgeschöpft“ wird. Es wird hieraus also unmittelbar deutlich, dass die Energie in den globalen Zirkulationen von Atmosphäre und Ozeanen auf der Tagseite der Erde zusammen mit der Temperaturgenese „wiederaufgeladen“ wird.

Soweitsogut, aber in dieser Abschätzung steckt ein grundsätzlicher Fehler. Eine S-B-Inversion ist allein schon geometrisch eine heikle Angelegenheit, die ich mit meinem hemisphärischen S-B-Modell gelöst hatte. Aber das einfallende solare HF-Spektrum unterscheidet sich bei gleicher spezifischer Strahlungsleistung in (W/m²) im Frequenzinhalt ganz gewaltig von dem IR-Spektrum für eine terrestrische S-B-Inversion:

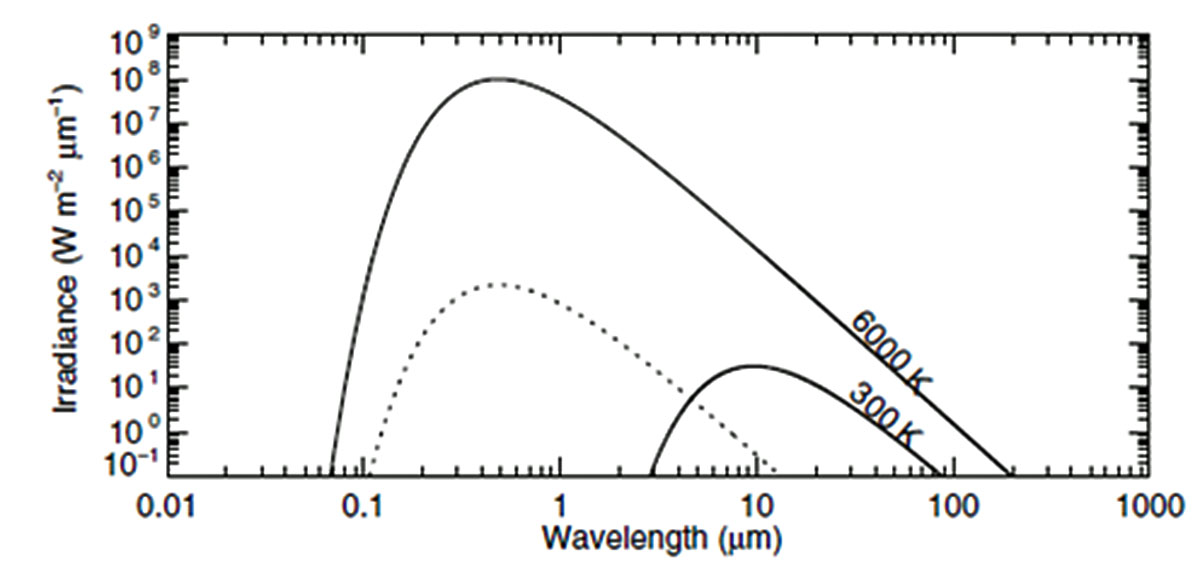
Abbildung 2: Die Planck-Funktionen für das solare 6.000K-HF-Spektrum der Sonnenoberfläche und an der Obergrenze der Erdatmosphäre (TOA) im Vergleich mit einem terrestrischen 300K-IR-Spektrum für die IR-Abstrahlung von der Erdoberfläche (EO) – Quelle: Abbildung 1.4 aus dem Lehrbuch von Bohren & Clothiaux (2006), „Fundamentals of Atmospheric Radiation“ (ISBN-13 ‏ : ‎ 978-3527405039)

Der Betrag der terrestrischen Abstrahlungsleistung dürfte in dieser Grafik korrekt dargestellt worden sein, schließlich sollte dort sowohl der Anteil der Albedo von 30% für das einfallende Solarspektrum als auch die IR-Abstrahlung über die gesamte Erdoberfläche berücksichtigt worden sein. Denn die solare Einstrahlung findet über eine Kreisfläche mit dem Erdradius auf die Tagseite der Erde statt, während die terrestrische Abstrahlung über eine Kugelfläche mit dem Erdradius erfolgt.

Wir müssen aber feststellen, dass sich die Spektren der solaren Einstrahlung @TOA und der terrestrischen Abstrahlung @EO in der Wellenlänge, respektive Frequenz, ganz wesentlich voneinander unterscheiden. Eine korrekte S-B-Inversion würde nun ein IR-Spektrum irgendwo zwischen 3 und 90 Mikrometern Wellenlänge erfordern, das einfallende solare HF-Spektrum liegt mit 0,1 bis 12 Mikrometern aber deutlich darunter. Schauen wir uns zunächst einmal die IR-Strahlung im Überschneidungsbereich beider Spektren genauer an. Man unterscheidet technisch drei unterschiedliche IR-Strahlungsarten:

Infrarote A-Strahlung: 0,78 bis 1,4 Mikrometer

Infrarote B-Strahlung: 1,4 bis 3 Mikrometer

Infrarote C-Strahlung: 3 bis 1.000 Mikrometer

Die technische Wirkung dieser drei IR-Strahlungsbereiche ist nachstehend in Abbildung 3 aufgelistet:

Abbildung 3: Die Wirkung der unterschiedlichen IR-Strahlungstypen A, B und C

Quelle: Internetauftritt der Fa. VASNER, Verl

Dabei wird die erzeugte Wärme erwartungsgemäß durch Wärmeleitung, Strahlung und Konvektion übertragen:

Abbildung 4: Typische Wärmeabgabe von IR-Heizungen in der Praxis

Quelle: Infrarotheizung und Strahlungswirkungsgrad – BVIR Bundesverband Infrarot-Heizung e. V.

Der wesentliche Teil des Überschneidungsbereiches beider Spektren fällt also in den Bereich der infraroten C-Strahlung, also des energieärmsten IR-Bereichs. Wenn elektromagnetische Strahlung als Photonenstrom betrachtet wird, dann ist die Energie eines Photons proportional zur Frequenz der elektromagnetischen Welle. Die Frequenz einer elektromagnetischen Welle ist abhängig von deren Wellenlänge:

ν = c / λ ν=Frequenz, c= Lichtgeschwindigkeit und λ=Wellenlänge

E = h ν Energie eines Photons mit h=Planck-Konstante und ν=FrequenzE = h ⋅ f

Für die Energie E eines Spektrums ist dagegen die Verteilung der Photonen über den gesamten Frequenzbereich maßgeblich:

Qe ≅ E = h Energie einer spektralen Verteilung

Wir stellen also zunächst einmal fest, dass das amplitudenreduzierte solare 6.000K-HF-Spektrum der solaren Einstrahlung @ TOA im Vergleich mit der in der hemisphärischen S-B-Inversion verwendeten spezifischen IR-Strahlungsleistung einen deutlich höheren Frequenzinhalt besitzt. Aber das Stefan-Boltzmann-Gesetz gilt nun einmal nur für die Beziehung zwischen der Temperatur eines Schwarzkörpers und dessen eigener spezifischer Schwarzkörper-Strahlungsleistung, die im Fall unserer Erde im infraroten Strahlungsbereich liegt. Bevor jetzt aber die THE-Anhänger in Freudentränen aus­brechen, kann ich glücklicherweise eine Menge Wasser in deren Wein schütten. Denn der vorstehend herausgearbeitete spektrale Widerspruch für eine terrestrische S-B-Inversion des solaren Strahlungsspektrums gilt natürlich genauso für das THE-Paradigma, und zwar gleichgültig, in welcher Form dieses ausgedrückt wird:

  • In den globalen 24h-Durchschnitt für die solare Strahlungsleistung und einer nachfolgenden S-B-Inversion mit (-18°C) geht ebenfalls der höhere Frequenzinhalt des solaren HF-Spektrums @TOA ein, wobei hier und im nachfolgenden Punkt weiterhin die Erklärung für die vektorielle Umkehr von HF zu IR fehlt.
  • Auch bei der reinen IN=OUT-Argumentation für die terrestrische Abstrahlung, also einer Energieverteilung ohne terrestrische Temperaturgenese und das Ablesen der Temperatur von (-18°C) aus der S-B-T4-Funktion, geht ebenfalls lediglich der Betrag des solaren HF-Spektrums @TOA ein, nicht aber dessen höherer Frequenzinhalt.
  • Und bei einer breitenabhängigen 24h-Mittelung der Sonneneinstrahlung geht ebenfalls lediglich der Nominalbetrag des einfallenden solaren HF-Spektrums @TOA ein und nicht dessen höherer Frequenzinhalt.

Es trifft also nicht nur mein hemisphärisches Stefan-Boltzmann-Modell, sondern auch alle THE-Modelle. Nur, mein Modell kommt dabei deutlich besser weg, als die THE-Modelle, denn dieses Modell stellt nach den vorstehenden Erkenntnissen ein Worst-Case-Szenario dar. Durch den höheren Frequenzinhalt des solaren Spektrums kann die aus der S-B-Inversion berechnete Temperatur nämlich nicht niedriger werden, als sie mit der hemisphärischen S-B-Inversion bereits berechnet wurde, sondern die berechnete Temperatur stellt vielmehr ein Temperaturminimum dar, das sich in der Realität bestenfalls nach oben verändern könnte. Da aber die hemisphärische S-B-Inversion über ein erdähnliches IR-Spektrum bereits ausreicht, um den THE zu widerlegen, bleibt die daraus abgeleitete Kernaussage voll erhalten. Anders ist es mit den THE-Paradigmen, die alle eine antiphysikalische Temperatur­erhöhung um 33°C für ihren THE postulieren. Durch den höheren Frequenzinhalt des solaren Inversionsspektrums könnte dieser Wert möglicherweise so nicht mehr haltbar sein. Vielmehr könnte der heilige CO2-Ungeist plötzlich ganz heftig gerupft werden und brächte damit einen Erklärungsnotstand über seine Jünger.

Wenden wir uns jetzt einmal dem Verlauf der Tagestemperatur zu. Dazu heißt es auf Wikipedia unter „Tagesgang“, Zitat mit Hervorhebungen:

„Der Tagesgang der Lufttemperatur ist direkt an den Tagesgang der Globalstrahlung gekoppelt und zeigt daher einen ausgeprägten Abfall in der Nacht, also nach Sonnenuntergang. Das Minimum wird dabei am frühen Morgen bzw. um den Sonnenaufgang herum erreicht. Diese Tendenz wird durch eine starke Bewölkung und auch Wind, besonders in Nähe größerer Wasseroberflächen, abgedämpft. Unterschreitet die Lufttemperatur dabei die Taupunkttemperatur, kann es zu Phänomenen wie Nebel, Tau oder Reif kommen. Nachdem die Temperatur ihr Tagesminimum durchschritten hat, steigt sie zunächst rasch und in den Mittagsstunden dann etwas langsamer an. Ihr Maximum erreicht sie nach dem Sonnenhöchststand, im Winter meist schon zwischen 13 und 14 Uhr, im Sommer zwischen 16 und 17 Uhr, teilweise erst vor 18 Uhr. Danach sinkt sie in den Abendstunden rasch und in der Nacht etwas langsamer ab, bis sie wiederum am frühen Morgen ihr Minimum erreicht. Dieser Normalfall des Tagesgangs gilt sowohl für den Sommer als auch für den Winter. Dynamische Einflüsse wie ein Einbruch von Warm- oder Kaltluft können aber zu teils erheblichen Abweichungen und unter Umständen einer Umkehr des Temperaturverlaufs führen. In Küstennähe ist der Seewind dafür verantwortlich, dass die Tageshöchsttemperatur oft schon wesentlich früher um 12 bis 13 Uhr erreicht wird, die Temperatur im weiteren Tagesverlauf also nicht mehr zunimmt.“

So, und mit diesem Wissen schauen wir uns nun einmal 10-Minuten-Werte für die Temperatur am 15. August 2001 in Berlin an:

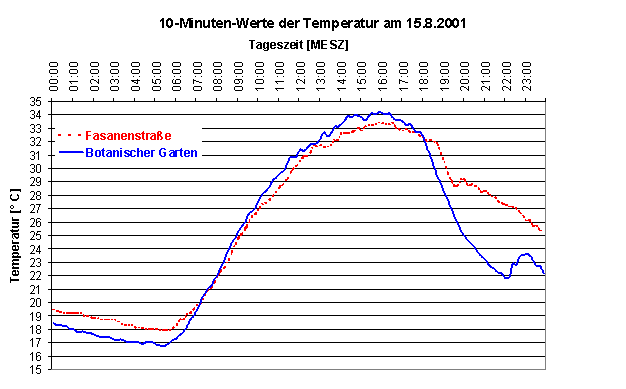
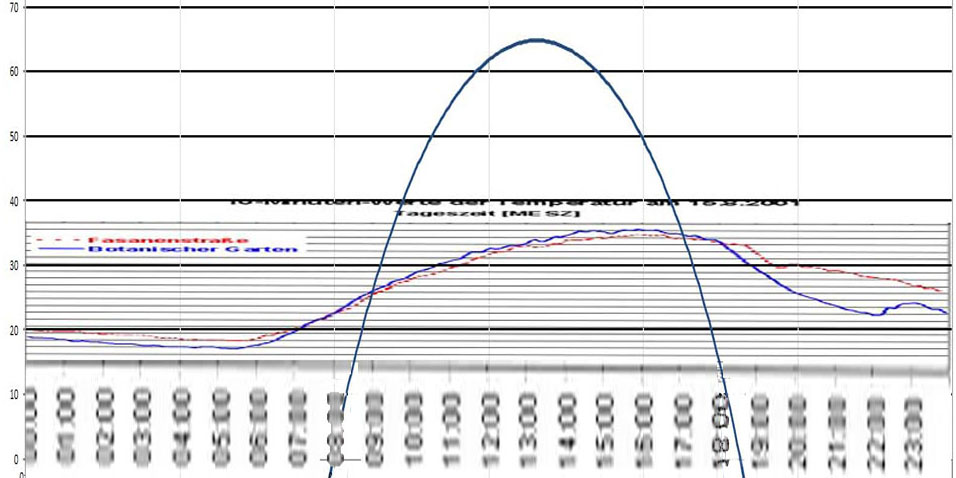
Abbildung 5: 10-Minuten-Werte für die Temperatur am 15. August 2001 in Berlin

Copyright: Alle Rechte vorbehalten, Freie Universität Berlin, 14195 Berlin: „Wir erlauben ausdrücklich und begrüßen das Zitieren unserer Dokumente und Webseiten sowie das Setzen von Links auf unsere Website.“

Mit den nachfolgend aufgeführten Eckdaten für Berlin vom 15. August 2001 habe ich dann einmal den vergleichbaren Tagesverlauf für das S-B-Temperaturäquivalent der solaren Einstrahlung berechnet, und zwar mit:

Solare Daten für Berlin am 15. August 2001

Solar Noon 13:10 MESZ

Erhebung Sonne 51 Grad

Mittagsrichtung 180 Grad

Sonnenaufgang 05:48 MESZ

Sonnenuntergang 20:31 MESZ

Tageslänge 14:42:59 Stunden

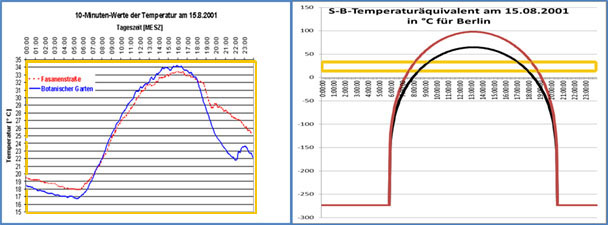
Abbildung 6: Vergleich der gemessenen Temperatur in Berlin (links: FU Berlin) mit dem S-B-Temperaturäquivalent für Berlin am 15. August 2001 (rechts: UW /rot=ohne Albedo / schwarz=mit Albedo) – gelb: Vergleich für die unterschiedlichen Vertikalmaßstäbe links & rechts

Wenn man diese beiden Diagramme dann einmal übereinander projiziert, ergibt sich das nachfolgende Bild:

Abbildung 7: Direkter Vergleich der gemessenen Temperatur in Berlin (FU Berlin) mit dem S-B-Temperaturäquivalent mit Albedo für Berlin am 15. August 2001 (schwarz)

Der Verlauf der gemessenen Tagestemperatur in Abbildung 6 lässt sich in fünf Abschnitte unterteilen:

  1. Die Temperatur fällt von 00:00 Uhr zum Sonnenaufgang um 05:50 Uhr leicht ab.
  2. Sofort von Sonnenaufgang an findet ein Anstieg der Temperatur statt, der sich zum Mittag hin langsam abflacht und seinen Zenit erst nach 16:00 Uhr erreicht. Dabei fällt insbesondere auf, dass sich die Temperatur morgens bereits erhöht, bevor das dafür eigentlich erforderliche S-B-Strahlungsäquivalent erreicht ist.
  3. Das Temperaturmaximum wird etwa 3 Stunden nach Solar Noon erreicht. Erst danach erfolgt zwischen etwa 16:30 Uhr und 18:00 Uhr ein flacher Abfall der Temperatur.
  4. Ein steilerer Temperaturabfall zwischen 18:00 und 22:00 Uhr, der langsam wieder abflacht.
  5. Ein leichtes Zwischenmaximum nach Sonnenuntergang zwischen 22:00 und 24:00 Uhr im Botanischen Garten, das wohl als Artefakt anzusehen ist.

Wir betrachten jetzt nur den Abschnitt [2], der sicherlich das markanteste Ereignis darstellt, weil sich hier die Temperatur beider Meßstationen bereits direkt nach Sonnenaufgang erhöht, obwohl rein physikalisch nach Verständnis des S-B-Gesetzes die spezifische Strahlungsleistung der Sonne noch gar keinen so frühen Beitrag zu einem Temperaturanstieg liefern dürfte. Nach der vorausgegangenen Diskussion kann es sich dabei eigentlich nur um einen Effekt des höherfrequenten solaren HF-Spektrums handeln, das trotz seiner vergleichbaren spezifischen Strahlungsleistung offenbar in der T^4-Funktion von Stefan und Boltzmann in seiner Wirkung nicht korrekt abgebildet wird.

Das ist bitter, denn jetzt haben wir noch ein weiteres Problem mit der terrestrischen S-B-Inversion des solaren HF-Spektrums:

  1. Wir haben festgestellt, dass der Beitrag des einfallenden solaren HF-Spektrums zur örtlichen Temperatur bereits kurz nach Sonnenaufgang beginnt, obwohl das terrestrische IR-Strahlungsäquivalent aus der Ortstemperatur für eine Erhöhung derselben noch gar nicht erreicht ist (S. Abbildung 1).
  2. Wir haben es bei vergleichbarer absoluter spezifischer Strahlungsleistung zu einem terrestrischen IR-Schwarzkörperspektrum also mit einem solaren HF-Spektrum geringerer Entropie zu tun.
  3. Ein terrestrisches IR-Spektrum würde von einer Stefan-Boltzmann-Inversion zwar korrekt abgebildet werden, nicht aber die S-B-Inversion eines solaren HF-Spektrums mit vergleichbarer absoluter spezifischer Strahlungsleistung.

Anmerkung: Wird hier etwa entgegen dem 2.HS der Thermodynamik etwas Wärmeres durch etwas Kälteres erwärmt? – Mitnichten, denn der wärmere Körper „Sonne“ bestrahlt den kälteren Körper „Erde“ mit seinem HF-Schwarzkörperspektrum von 5.772 Kelvin. Durch die sphärische Divergenz über die Entfernung zur Erdumlaufbahn beträgt die Solarkonstante auf der Erde allerdings nur noch 1.367 W/m². Wir haben hier auf der Erde also ein solares HF-Schwarzkörperspektrum mit einem Absolutbetrag von 1.367 W/m², dessen spezifische Strahlungsleistung als IR-Schwarzkörperspektrum bei einer terrestrischen S-B-Inversion maximal 394 Kelvin (=121°C) erzeugen könnte.

Was bedeutet das nun?

  1. Möglicherweise kann das solare Spektrum hier auf der Erde bereits einen Temperaturanstieg erzeugen, bevor es das rechnerische S-B-Temperaturäquivalent die Ortstemperatur überschreitet.
  2. Andererseits ist bisher nirgendwo berichtet worden, dass die Schutzwirkung von Raumanzügen gegen eine solare Einstrahlung von 1.367W/m² entsprechend 121°C bei den Außenarbeiten der Astronauten nicht ausgereicht hätte.

Was kann man da jetzt tun? Nun, da es sich in Abbildung 5 um ein einziges 24h-Temperaturdiagramm für lediglich zwei Meßstationen handelt, gibt es eigentlich nur folgende Möglichkeiten:

  1. Der unter [2] beschriebene frühzeitige Temperaturanstieg ist ein Artefakt und kann getrost ignoriert werden.
  2. Eine terrestrische Stefan-Boltzmann-Inversion kann nach Argument [7] das solare HF-Spektrum nicht korrekt abbilden.
  3. Zwar ist das maximale S-B-Temperaturäquivalent einer terrestrischen S-B-Inversion des einfallenden solaren HF-Spektrums nach Argument [10] auf den Betrag der spezifischen Strahlungsleistung beschränkt, aber insgesamt steigt die Temperaturkurve steiler an und das Maximum wird breiter, als es das Stefan-Boltzmann-Gesetz vorgibt

Es wäre also eine Aufgabe für die Experimentalphysik herauszufinden, welcher der drei Lösungsansätze bzw. deren Kombination [I], [II] und/oder [III] die physikalische Realität abbilden kann oder ob sich vielleicht noch eine ganz andere Lösung dieser Problematik anbietet.

Meine Anforderung an die Experimentalphysik: Die Experimentalphysik wird höflich gebeten, die hier formulierten Lösungsansätze [I], [II] und/oder [III] für die solare S-B-Inversion einmal unter dem Einsatz unterschiedlicher Einstrahlungsspektren mit gleicher spezifischer Strahlungsleistungen zu überprüfen und damit entweder zu verifizieren oder zu verwerfen. Für den Versuchsaufbau wird eine beidseitig geschwärzte dünne und beheizte Metallplatte vorgeschlagen, die von der einen Seite mit Schwarzkörperspektren unterschiedlicher Frequenzbereiche bei jeweils aufsteigender Strahlungsleistung erwärmt wird, und deren Gleichgewichtstemperatur auf der anderen Seite gemessen wird.

In einer Fortsetzung dieses Artikels werden weitere 24h-Temperaturmessungen vorgestellt und untersucht, ob der hier beschriebene frühzeitige Erwärmungseffekt unterhalb des solaren S-B-Strahlungsäquivalents der Ortstemperatur bestätigt werden kann.