Krampfhafte Suche nach Hockeyschlägern
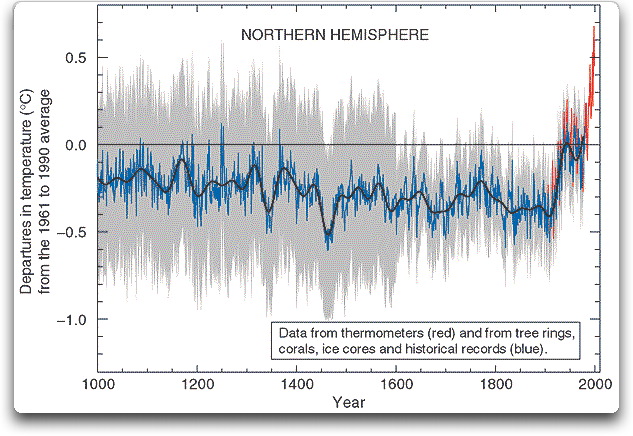
Der legendäre „Hockeyschläger“ weigert sich einfach zu sterben. Er wurde erstmals von Mann, Bradley und Hughes in ihrer 1998 veröffentlichten Arbeit „Global-scale temperature patterns and climate forcing over the past six centuries“ (im Folgenden „MBH98“) erschaffen.
MBH98 behauptete zu zeigen, dass sich die Welt nach einem langen Zeitraum mit sehr geringen Veränderungen plötzlich zu erwärmen begann, und zwar schnell.
Vor ein paar Jahrzehnten leistete Steve McIntyre von Climate Audit wirklich ganze Arbeit, indem er eine Vielzahl von Fehlern in MBH98 aufdeckte. Und irgendwann in dieser Zeit stellte jemand, wahrscheinlich Steve, aber vielleicht auch jemand anderes fest, dass das merkwürdige (und mathematisch falsche) in MBH98 verwendete Verfahren aktiv Hockeysticks aus dem roten Rauschen herausarbeiten konnte.
Trotz alledem folgten auf MBH verschiedene Studien, die ich als „Hockeyschläger“ bezeichne, d. h. Studien, die vorgaben, unabhängig voneinander einen Hockeyschläger in den historischen Aufzeichnungen zu finden, und von denen daher behauptet wurde, sie würden den ursprünglichen Hockeyschläger von MBH98 unterstützen und validieren.
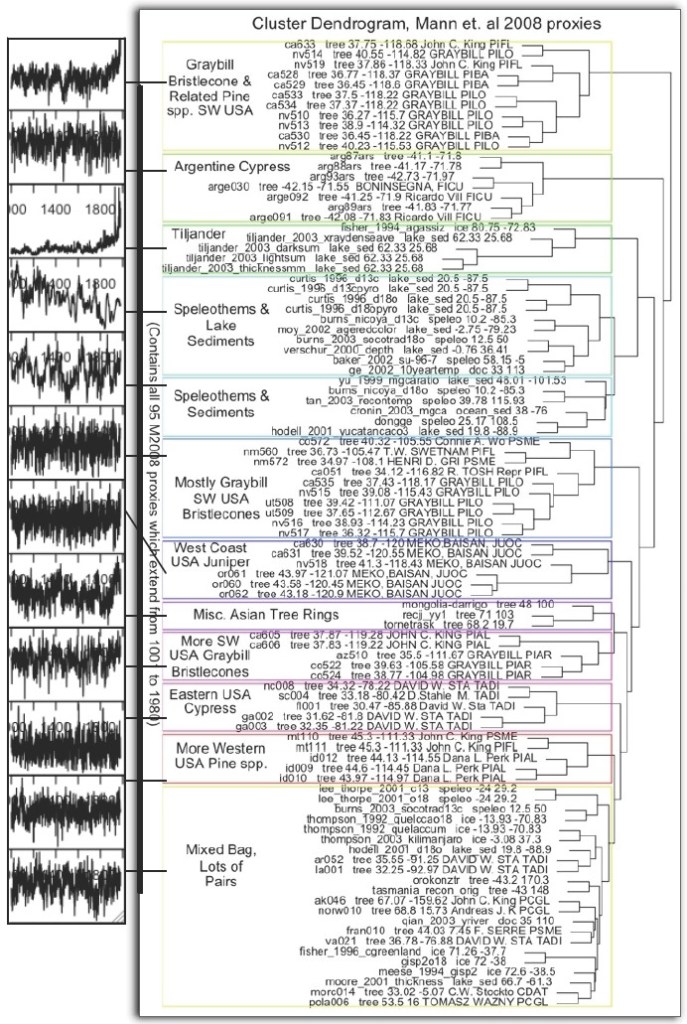
Natürlich wiederholten diese Studien viele der gleichen Fehler, die von McIntyre und anderen aufgedeckt worden waren. Hier ist die Geldgrafik aus meinem Beitrag Kill It With Fire, in dem der Versuch von Mann 2008 analysiert wurde, den Hockeystick zu rehabilitieren (M2008):
Man beachte, dass die Hockeystick-Form nur von einigen wenigen Gruppen von Proxies abhängt.
Vor ein paar Tagen wurde mir klar, dass ich zwar geglaubt hatte, dass die fehlerhafte Mathematik von MBH98 Hockeysticks aus dem roten Rauschen herausarbeiten zu können, es aber nie selbst ausprobiert hatte. Und was noch wichtiger ist, ich hatte es nie mit einfacheren Berechnungen versucht, mit einfachen Durchschnittswerten anstelle des unzentrierten Hauptkomponenten-Verfahrens von MBH98. Dies ist also im Grunde mein Labornotizbuch aus dieser Untersuchung.
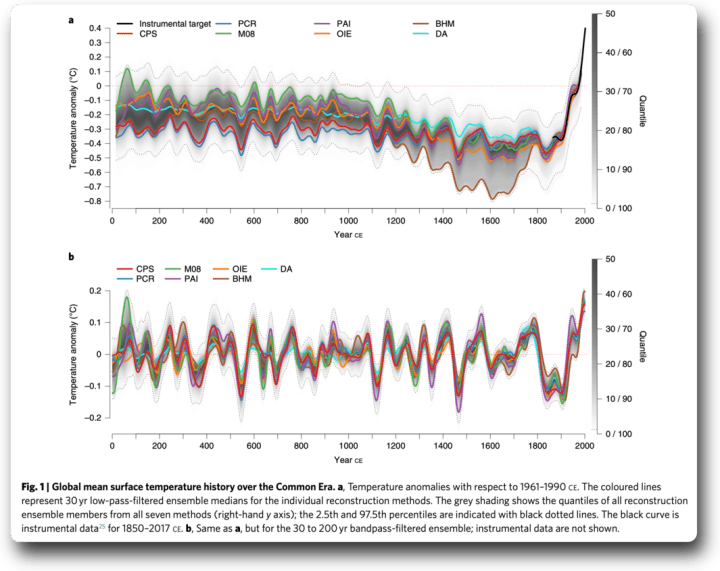
Der umfangreichste dieser Hockeyschläger betrifft den PAGES-Datensatz, den es in drei Varianten gibt: PAGES2017, PAGES2019 und PAGES2K. PAGES2K beginnt im Jahr 1 n. Chr. und enthält mehr als 600 Proxydaten. Hier sind mehrere PAGES2K-Rekonstruktionen aus einem Nature-Artikel, der die Behauptung aufstellt, dass es eine „konsistente multidekadische Variabilität in globalen Temperaturrekonstruktionen und -simulationen über das gemeinsame Zeitalter“ gibt:
Wie Abbildung 3 zeigt, ist es wahr, dass verschiedene Untersuchungen von unterschiedlichen Teams sehr ähnliche Hockeystick-Formen ergeben haben. Dies scheint die Wissenschaftler sehr zu beeindrucken, aber in diesem Beitrag wird gezeigt, warum dies sowohl wahr als auch bedeutungslos ist.
Dazu müssen wir zunächst die einzelnen Schritte bei der Erstellung historischer Temperaturrekonstruktionen auf der Grundlage von Proxys verstehen. Ein „Proxy“ ist eine Messung von Unterschieden in einer messbaren Variable, die sich mit der Temperatur ändert. Wenn es zum Beispiel wärmer ist, wachsen Bäume und Korallen im Allgemeinen schneller. Daher können wir die Breite ihrer Jahresringe als Stellvertreter für die Umgebungstemperatur analysieren. Andere Temperaturproxys sind Isotope in Eisbohrkernen, Sedimentationsraten in Seen, Speläotheme, Magnesium/Kalzium-Verhältnisse in Muscheln und ähnliches.
Der Prozess der Erstellung eines historischen Datensatzes auf der Grundlage von Proxys geht folgendermaßen vor sich:
1. Sammeln Sie eine Reihe von Proxys.
2. Verwerfen Sie diejenigen, die nicht „temperatursensitiv“ sind. Temperatursensitive Proxies können identifiziert werden, indem man prüft, ob sie im Allgemeinen im Gleichschritt (oder gegen den Gleichschritt) mit historischen Temperaturbeobachtungen schwanken (hohe Korrelation).
3. Sie können positiv korreliert sein (Temperatur und Proxy steigen/fallen gemeinsam) oder negativ korreliert (wenn das eine steigt, fällt das andere). Beide reagieren empfindlich auf die Temperatur und sind daher nützlich. Wir müssen also einfach die Proxies mit negativer Korrelation umdrehen.
4. Verwenden Sie ein einfaches oder komplexes mathematisches Verfahren, um den Durchschnitt aller oder einer Teilmenge der einzelnen Proxies zu ermitteln.
5. Erklären Sie den Erfolg.
[Hervorhebungen im Original]
Das scheint eine vernünftige Idee zu sein. Man sucht nach temperatursensiblen Proxies und mittelt sie auf irgendeine Weise, um die Vergangenheit zu rekonstruieren. Also … was gibt es da zu beanstanden?
Zunächst einmal hier die Beschreibung aus der Studie, in dem PAGES2K angekündigt wird, mit dem Titel „A global multiproxy database for temperature reconstructions of the Common Era„:
Reproduzierbare Klimarekonstruktionen für die Common Era (1. Jh. n. Chr. bis heute) sind der Schlüssel, um die Erwärmung in der Industrie-Zeitalter in den Kontext der natürlichen Klimavariabilität zu stellen.
Hier stellen wir eine von der Gemeinschaft bereitgestellte Datenbank mit temperatursensitiven Proxydaten aus der PAGES2k-Initiative vor. Die Datenbank enthält 692 Datensätze aus 648 Orten, darunter alle Kontinentalregionen und die wichtigsten Meeresbecken. Die Aufzeichnungen stammen von Bäumen, Eis, Sedimenten, Korallen, Speläothemen, dokumentarischen Belegen und anderen Archiven. Ihre Länge reicht von 50 bis 2000 Jahren, mit einem Median von 547 Jahren, während die zeitliche Auflösung von zweiwöchentlich bis hundertjährlich reicht. Fast die Hälfte der Proxy-Zeitreihen sind signifikant mit der HadCRUT4.2-Temperatur im Zeitraum 1850-2014 korreliert.
PAGES2K hat also den ersten Schritt zur Erstellung einer proxy-basierten Temperaturrekonstruktion vollzogen. Sie haben eine Vielzahl von Proxies gesammelt und festgestellt, dass etwa die Hälfte von ihnen „temperaturempfindlich“ sind, basierend auf ihrer Übereinstimmung mit der HadCRUT-Temperatur.
Nochmals … was gibt es da zu beanstanden?
Um zu demonstrieren, was es zu beanstanden gibt, habe ich Gruppen von 692 „Pseudoproxies“ erstellt, die der Größe des PAGES2K-Datensatzes entsprechen. Dabei handelt es sich um nach dem Zufallsprinzip erzeugte „Zeitreihen“, die im Jahr 1 beginnen, um der Länge des PAGES2K-Datensatzes zu entsprechen. Ich habe sie so erstellt, dass ihre Autokorrelation in etwa mit der Autokorrelation der Temperaturaufzeichnungen übereinstimmt, die recht hoch ist. Auf diese Weise sind sie „lebensecht“, eine gute Übereinstimmung mit den tatsächlichen Temperaturaufzeichnungen. Hier sind die ersten zehn einer zufälligen Gruppe:
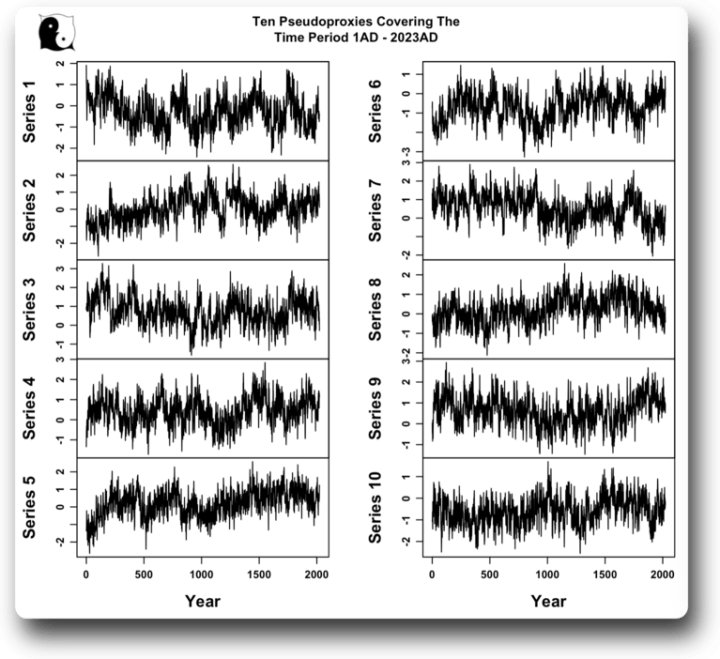
Abbildung 4. Nach dem Zufallsprinzip erzeugte Pseudoproxies mit hoher Autokorrelation, auch „rotes Rauschen“ genannt.
Wie man sieht, könnten sie alle die zwei Jahrtausende lange Temperaturgeschichte eines imaginären Planeten repräsentieren. Wie gut ist ihre Korrelation mit den Temperaturbeobachtungen? Abbildung 5 zeigt diese Daten:
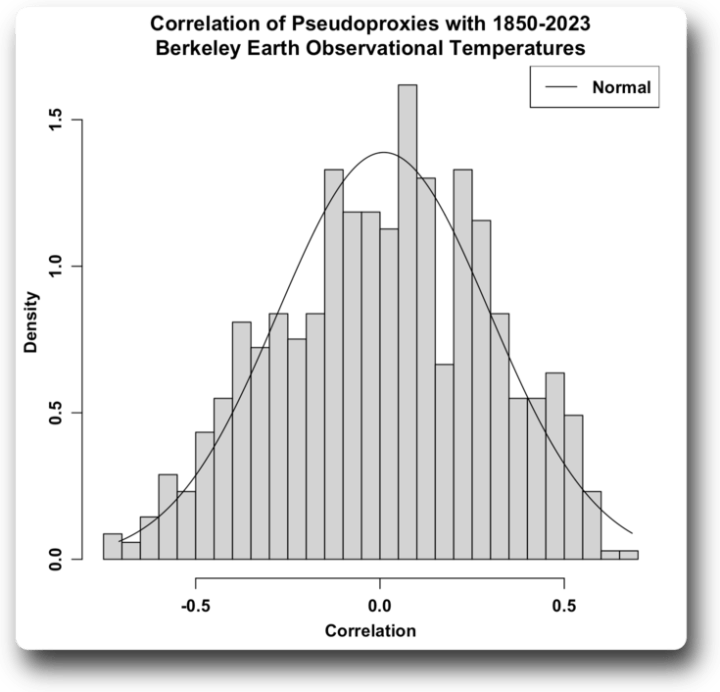
Abbildung 5. Korrelationen von 692 zufälligen Pseudoproxies mit den modernen Temperaturbeobachtungen von Berkeley Earth.
Dies entspricht in etwa dem, was wir erwarten würden: Etwa die Hälfte der Pseudoproxies weist eine positive Korrelation mit den Temperaturbeobachtungen auf, die andere Hälfte eine negative Korrelation, und die meisten Proxies weisen keine starke Korrelation mit der Temperatur auf.
Und hier ist der Durchschnitt aller Pseudoproxies:
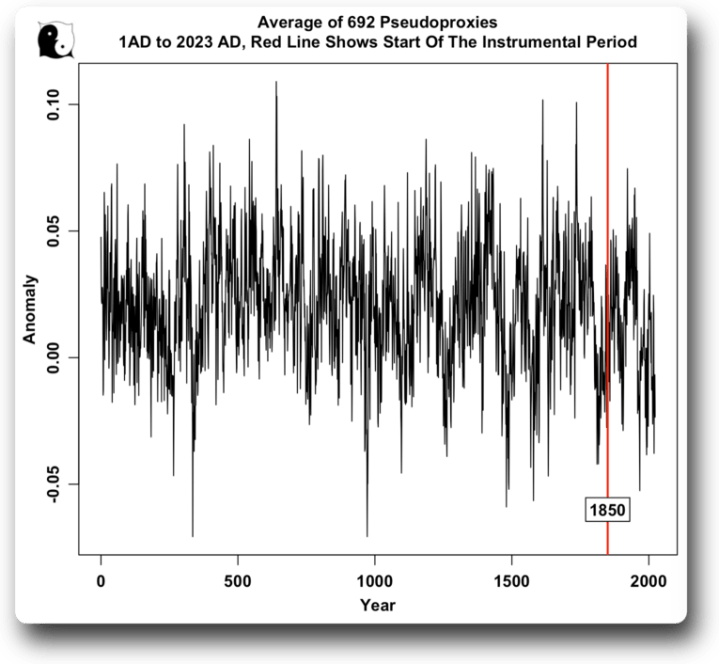
Abbildung 6. Durchschnitt, 692 Pseudoproxies. Die rote Linie zeigt den Beginn der instrumentellen Aufzeichnung von Berkeley Earth. Man beachte, dass es keinen Hockeyschläger gibt – im Gegenteil, in diesem Fall habe ich, um eine Verzerrung meiner Ergebnisse zu vermeiden, eine Reihe von Pseudoproxies ausgewählt, deren Durchschnitt am jüngsten Ende abfällt. Es gibt auch keinen signifikanten Trend in den Gesamtdaten.
OK, wir haben also die Proxies, und wir haben die Korrelation jedes einzelnen mit der instrumentellen Aufzeichnung berechnet. Dann habe ich in Schritt 3 des oben beschriebenen Verfahrens diejenigen Proxies umgedreht, die eine negative Korrelation mit dem instrumentellen Datensatz aufwiesen. Das bedeutete, dass alle Proxies positiv mit den Berkeley Earth-Daten korreliert waren.
An diesem Punkt wollte ich sehen, wie ein Durchschnitt aussehen würde, wenn ich nur die Pseudoproxies mit einer hohen Korrelation mit der instrumentellen Aufzeichnung auswählen würde, sagen wir 0,5 oder mehr, … aber vorher dachte ich ohne besonderen Grund, dass ich mir einen einfachen Durchschnitt des gesamten Datensatzes ansehen würde. Das hat mich verblüfft.
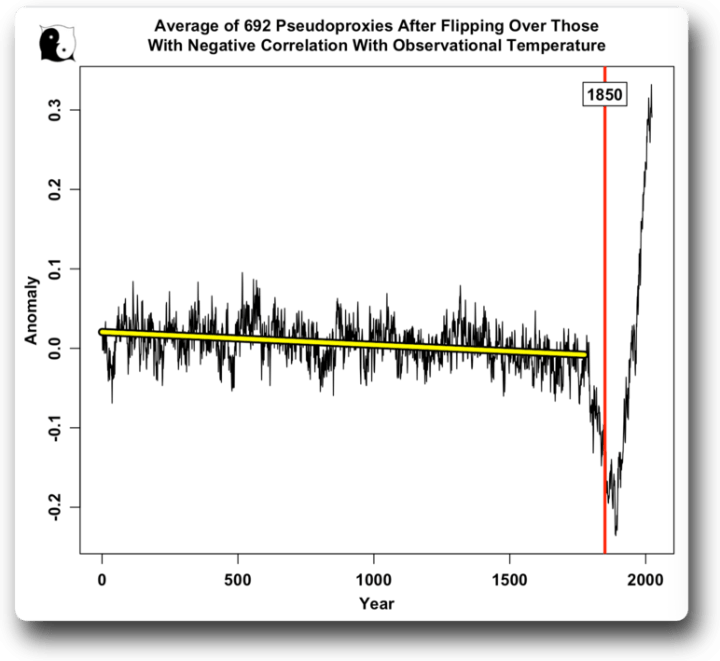
Abbildung 7. Durchschnitt aller Pseudoproxies nach einfachem Umdrehen (Invertieren) derjenigen, die eine negative Korrelation mit den Instrumentaldaten aufweisen.
HOPPLA!
Hier können wir sehen, warum alle verschiedenen Mittelungsmethoden die gleiche „historische Aufzeichnung“ ergeben … weil das oben genannte Verfahren aktiv nach Hockeyschlägern im zufälligen roten Rauschen sucht.
Ein interessantes Detail in Abbildung 7 ist, dass der Durchschnitt vor dem Beginn des für die Korrelation verwendeten Zeitraums stark abfällt. Ich nehme an, dies ist darauf zurückzuführen, dass für einen so starken Anstieg zunächst ein Tiefpunkt erreicht werden muss.
Und dieser Einbruch vor 1850 ist von Interesse, weil er sowohl in Panel A als auch in Panel B der in Abbildung 3 gezeigten PAGES2K-Rekonstruktionen zu sehen ist …
Ein weiterer bemerkenswerter Punkt ist, dass das Verfahren einen leichten Abwärtstrend von Anfang an bis zu einem starken Rückgang um 1775 eingeführt hat. Ich führe das darauf zurück, dass das Verfahren „U“-förmige Datensätze bevorzugt.
In jedem Fall ist der leichte Abwärtstrend ein echter Effekt des Verfahrens. Wir wissen das, weil es im gesamten Datensatz keinen Abwärtstrend gibt. Wir wissen auch, dass es sich um einen realen Effekt handelt, und zwar aus einem noch wichtigeren Grund: Wir sehen den gleichen leichten Abwärtstrend im ursprünglichen MBH-Hockeystick in Abbildung 1 und auch in Panel „a“ von Abbildung 2.
Und schließlich, warum gibt es so wenig Variation im „Griff“ des Hockeysticks? Sind die Temperaturen in der Vergangenheit wirklich so stabil?
Nein. Es handelt sich um ein weiteres Artefakt. Der Griff des Hockeysticks ist nur ein Mittelwert aus einer vermutlich großen Anzahl von zufälligen Datensätzen mit rotem Rauschen. Wenn man den Durchschnitt einer Reihe von zufälligen Datensätzen mit rotem Rauschen bildet, erhält man eine gerade Linie.
Mein nächster Gedanke war: Wie stark muss ich die Pseudoproxies beeinflussen, um einen sichtbaren Hockeyschläger zu erzeugen?
Um das zu untersuchen, habe ich den gleichen Originaldatensatz genommen. In diesem Fall habe ich jedoch nur 40 Proxies invertiert, und zwar diejenigen mit der stärksten negativen Korrelation. Ich habe also nur die stärksten negativen Signale umgedreht und den Rest der Proxies, die eine negative Korrelation aufwiesen, als unberührtes rotes Rauschen belassen. Hier ist das Ergebnis:
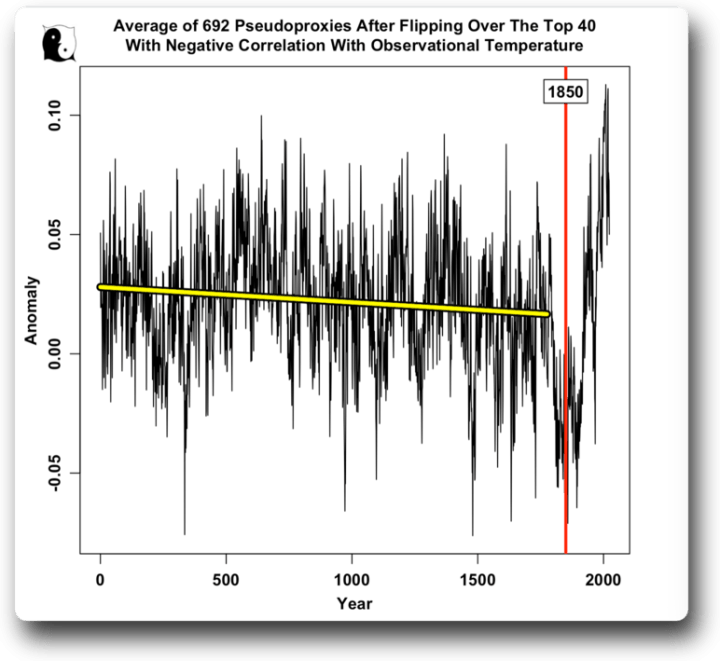
Abbildung 8. Durchschnitt aller Pseudoproxies nach Umdrehen derjenigen mit den vierzig höchsten negativen Korrelationen mit den Instrumentaldaten.
Man beachte, dass weniger als sechs Prozent (vierzig) der Pseudoproxies umgedreht wurden und alle vier Hockeyschläger-Merkmale bereits sichtbar sind – eine verringerte Variation im „Griff“ desselben, ein leichter Abwärtstrend bis 1775, ein starker Rückgang bis 1850 und eine fast vertikale „Blatt“ des Hockeyschlägers von 1850 an.
Wie sieht es am anderen Ende der Skala aus, wo wir nur die Daten mit der stärksten Korrelation auswählen? Hier ist der Durchschnitt nur des oberen Viertels der Daten (176 Pseudoproxies), gemessen an ihrer Korrelation mit der beobachteten Temperatur:
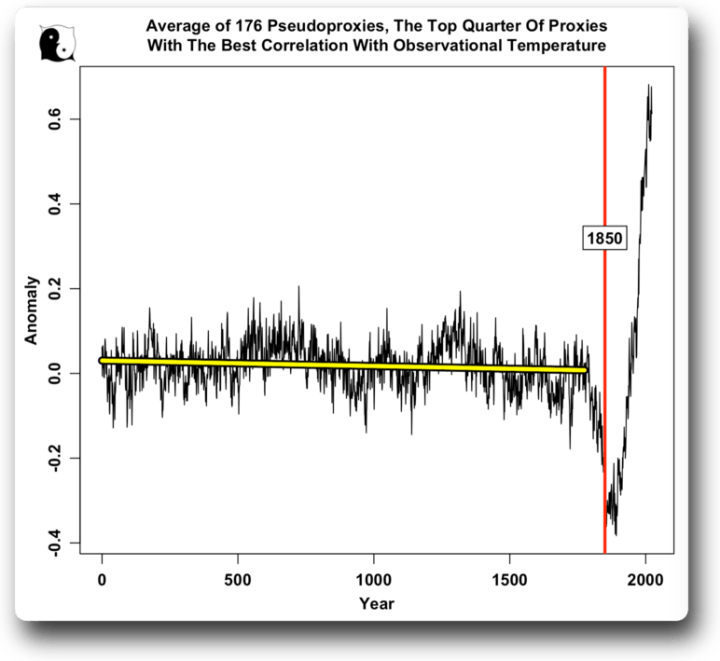
Abbildung 8a. Durchschnitt nur des obersten Viertels der Daten, d. h. derjenigen mit der besten Korrelation mit den Berkeley Earth-Daten.
Gleiche Sache. Gerader Griff am Hockeyschläger. Langsamer Rückgang bis 1775. Starker Rückgang. Vertikales Hockeyschläger-Blatt danach.
Schließlich wurde mir klar, dass ich mir die besten Szenarien angesehen hatte … aber was ist mit dem schlimmsten Fall? Hier ist also die Hälfte der Pseudoproxies mit der schlechtesten Korrelation mit der beobachteten Temperatur:
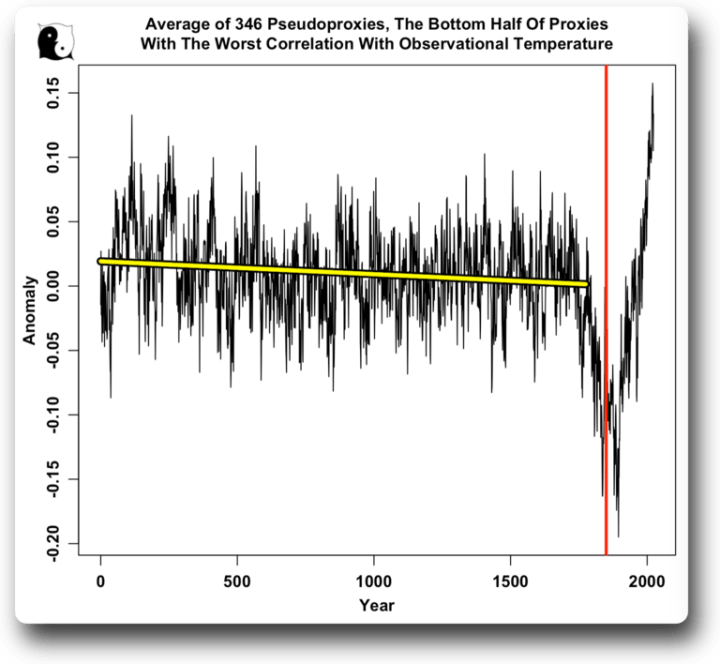
Abbildung 9. Durchschnitt nur der unteren Hälfte der Daten, derjenigen mit der schlechtesten Korrelation mit den Berkeley Earth-Daten.
Obwohl wir nur die Hälfte der Pseudoproxies mit der schlechtesten Korrelation mit den Temperaturen verwenden, nämlich diejenigen mit einer Korrelation von 0,22 oder weniger, erhalten wir die gleiche Geschichte wie zuvor – den gleichen geraden Hockeyschläger, den gleichen leichten Rückgang bis 1775, den gleichen starken Rückgang bis 1850 und das gleiche vertikale Hockeyschläger-Blatt nach 1850.
Es gibt einen interessanten und leicht zu übersehenden Punkt in den obigen Grafiken. Während die Form gleich bleibt, ist das Blatt des Hockeyschlägers umso höher, je größer die Korrelation ist. Die verschiedenen Verfahren veränderten die Spitze des Blattes von ~0,1, wenn nur 40 umgedreht wurden, über ~1,5, wenn die am schlechtesten korrelierten Pseudoproxies verwendet wurden, zu ~0,3, wenn alle Pseudoproxies umgedreht wurden, bis zu ~0,7, wenn nur die am besten korrelierten verwendet wurden. Alle zeigten also die gleiche Form des Hockeyschlägers, und sie unterschieden sich nur in der Größe des Blattes. Seltsam.
Ich habe weiter oben gesagt, dass dieser Beitrag zeigen würde, warum es sowohl wahr als auch bedeutungslos ist, dass verschiedene Studien alle zu Hockeyschlägern kommen.
Der Grund dafür ist in den obigen Zahlen ganz klar ersichtlich – egal, was die Forscher tun, da sie alle irgendeine Variante des Standardverfahrens verwenden, das ich oben im Beitrag aufgeführt habe, erhalten sie garantiert einen Hockeyschläger. Sie können dem nicht entkommen. Mit diesem Verfahren werden definitiv und sehr effektiv Hockeyschläger aus dem zufälligen roten Rauschen herausgefiltert.
[Hervorhebungen im Original]
Link: https://wattsupwiththat.com/2024/06/29/mining-for-hockeysticks/
Übersetzt von Christian Freuer für das EIKE