Evaluierung der Modellprojektionen
Jemand hat im Internet die Fähigkeiten der frühen Klimamodelle angepriesen und sich dabei auf die Studie Evaluating the Performance of Past Climate Model Projections von Zeke Hausfather, Henri F. Drake, Tristan Abbott und Gavin A. Schmidt bezogen.
Und ja, die Studie zeigt, dass die Klimamodelle wunderbar in der Lage sind, die Vergangenheit zurückzuverfolgen und die Zukunft vorherzusagen. Sie stellen eine Vielzahl von Tabellen und Grafiken zur Verfügung, um dies zu zeigen.
Aber ich war an etwas anderem interessiert. Ich wollte sehen, wie die vorübergehende Klimareaktion (Transient Climate Response, TCR) der einzelnen Modelle aussieht. Der IPCC definiert die vorübergehende Klimareaktion (TCR) als die globale Temperaturänderung zum Zeitpunkt einer Verdoppelung des Kohlendioxids (CO₂) in einem Experiment mit einem Anstieg von 1 % pro Jahr.
Mit anderen Worten, es handelt sich um die Temperaturänderung, die einer Erhöhung des Antriebs um 1 W/m² entspricht, multipliziert mit der Erhöhung des Antriebs um 3,7 W/m², die laut IPCC bei einer Verdoppelung des CO₂ eintreten wird.
Also habe ich mir die Modelldaten angesehen, die die Autoren sehr verantwortungsbewusst als Excel-Tabelle auf GitHub online gestellt haben, und die TCR für jedes analysierte Modell berechnet.
Dann wollte ich zusätzlich zur TCR die ECS, die Equilibrium Climate Sensitivity, berechnen. Dazu habe ich mir die TCR und die ECS von 23 Modellen aus dieser Studie angesehen. Hier sind diese Daten, zusammen mit einer LOWESS-Glättung der Daten:
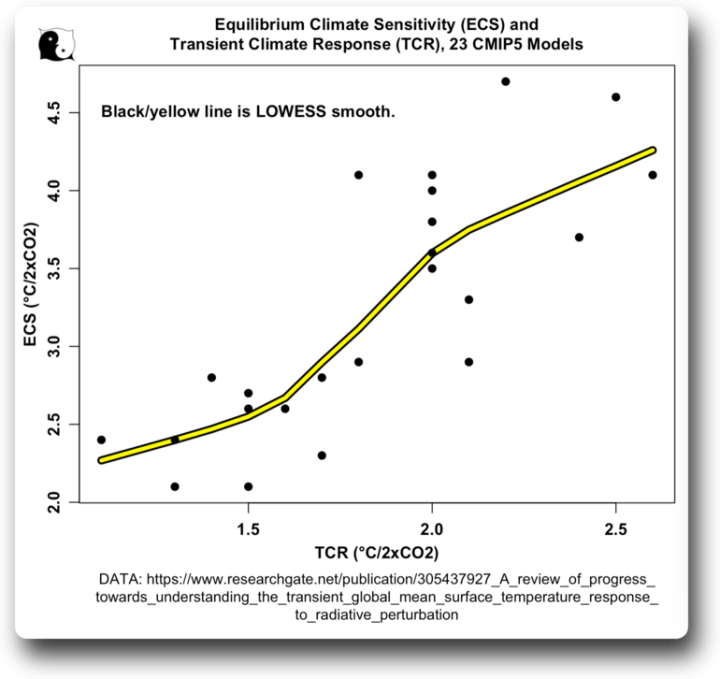
Abbildung 1. Streudiagramm, Gleichgewichts-Klimasensitivität (ECS) gegen transiente Klima-Reaktion (TCR), 23 CMIP-Modelle.
Daher habe ich die TCR-Werte aus der Modellleistungsstudie in ECS-Werte umgerechnet, wobei ich die LOWESS-Linie für die Umrechnung verwendet habe. Details in den Fußnoten.
Hier sind die Ergebnisse für die verschiedenen Modelle:

Abbildung 2. TCR und ECS für die 12 Modelle, die in der Studie zur Modellleistung untersucht wurden.
Das Interessante daran ist, dass die Klimasensitivität (ECS) der Modelle eine sehr große Spanne abdeckt, von zwei bis vier Grad bei einer Verdopplung des CO₂ … und dennoch leisten sie alle eine hervorragende Arbeit beim Hindcasting der Temperaturentwicklung des Planeten.
Und FALLS sie alle „physikalisch begründet“ sind, wie immer behauptet wird, tut es mir leid, aber das ist nicht möglich.
Ich nenne dies „Dr. Kiehl’s Paradox“, weil Jeffrey Kiehl 2007 in einem in GRL veröffentlichten Artikel mit dem Titel „Twentieth century climate model response and climate sensitivity“ (Reaktion des Klimamodells im zwanzigsten Jahrhundert und Klimasensitivität) diese Merkwürdigkeit zum ersten Mal bemerkte. Er sagte:
Die Frage ist: Wenn sich die Klimamodelle in ihrer Klimasensitivität um den Faktor 2 bis 3 unterscheiden, wie können sie dann alle die globale Temperaturaufzeichnung mit angemessener Genauigkeit simulieren?
Das ist in der Tat eine gute Frage. Als Antwort auf diese Studie habe ich einen Beitrag mit dem Titel „Dr. Kiehl’s Paradox“ geschrieben. Darin diskutierte ich Dr. Kiehls Antwort ebenso wie meine eigene Antwort auf diese Frage. Darauf folgten einige weitere Analysen mit den Titeln „Zero Point Three Times The Forcing“ (hier) und „Life Is Like A Black Box Of Chocolates“ (hier).
In diesen Beiträgen habe ich gezeigt, dass die globalen Temperaturergebnisse der Klimamodelle trotz ihrer immensen Komplexität sehr genau durch eine einzeilige Gleichung nachgebildet werden können, die einfach die als Input für die Modelle verwendeten Antriebsfaktoren verzögert und skaliert.
Ach ja, eine letzte Kuriosität. Im Hansen-Modell von 1981 sind die TCR und damit die ECS nicht konstant. Von 1981 bis 2024 steigt der ECS von etwa 1,6°C/2xCO₂ auf etwa 2,5°C/2xCO₂. Die ECS steigt dann bis 2040 weiter, geht bis 2075 leicht zurück und steigt bis 2100 auf 2,8°C/2xCO₂. Das ist fast das Doppelte des Ausgangswerts.
Was bedeutet das?
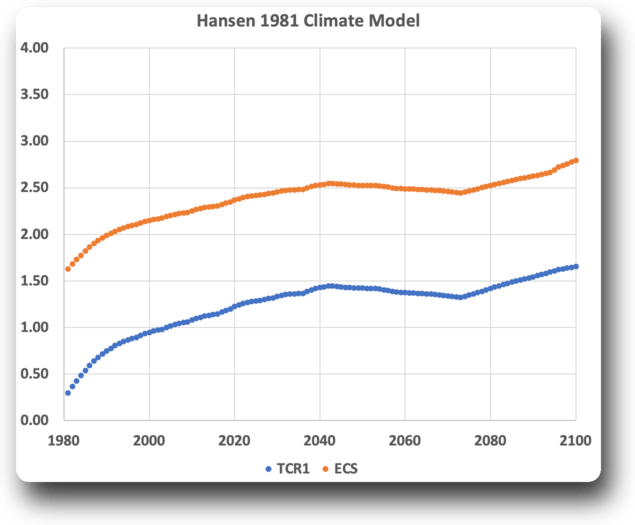
Abbildung 3. TCR und ECS für das Modell von Hansen 1981. Die TCS für jedes Jahr wird anhand der Veränderung von Treibhausgas und Temperatur von 1950 zu Treibhausgas und Temperatur für dieses Jahr berechnet.
Ich muss sagen, dass ich von der scheinbaren Übereinstimmung der Modelle mit der Realität nicht beeindruckt bin. Sie basieren nicht auf der Physik. Stattdessen sind sie einfach so eingestellt, dass sie mit der Vergangenheit übereinstimmen … und im Fall von Hansen 1981 so eingestellt, dass sie die zukünftige Erwärmung übertreiben.
Und wie mein genialer älterer Bruder zu sagen pflegte: „Es ist leicht, die Zukunft vorherzusagen … solange sie genau wie die Vergangenheit ist“.
Wie ich in meinem letzten Beitrag mit dem Titel Now You Sea Ice, Now You Don’t gezeigt habe (erscheint demnächst auch in deutscher Übersetzung), unterscheidet sich das Klima leider gelegentlich und ziemlich unvorhersehbar stark von der Vergangenheit …
Für die Mathematiker: Die Funktion, die ich in Excel verwendet habe, um den TCR in den ECS umzurechnen, basiert auf einer Annäherung an die LOWESS-Kurve in Abbildung 1. Sie lautet:
= IF(TCR < 1.6, 1.39 + 0.8 * TCR, IF(TCR < 2, -1.04 + 2.32 * TCR, 1.4 + 1.1 * TCR))
Damit werden drei annähernd geradlinige Abschnitte der LOWESS-Glättung definiert und deren Formeln zur Berechnung des ECS in Abhängigkeit vom TCR-Wert verwendet.
Link: https://wattsupwiththat.com/2024/04/20/evaluating-the-model-projections/
Übersetzt von Christian Freuer für das EIKE