Gibt es einen Atmosphärischen Treibhauseffekt? – Teil 2
Hermann Harde, Michael Schnell
Experimente mit Treibhausgasen
1. Versuchsaufbau für Messung mit Treibhaus-Gasen
Im Ersten Teil des Artikels „Gibt es einen Atmosphärischen Treibhauseffekt“ wurde eine einfache Apparatur vorgestellt, die sich von einem Styroporblock in einen Strahlungskanal mit verschiedenen Oberflächenbeschichtungen umwandeln lässt. Mittelpunkt der Untersuchungen war eine heizbare, warme Platte, die gleichzeitig als Wärmequelle und Sensor fungierte. Es konnte nachgewiesen werden, dass rund 70 % der elektrischen Heizleistung durch Strahlungsaustausch und 30 % durch Wärmeleitung von der warmen Platte abgeführt werden.
Der neue Versuchsaufbau besitzt einen wesentlich größeren Strahlungskanal aus poliertem Aluminium als Behälter für die untersuchten Gase. Ähnlich wie beim vorherigen Aufbau befinden sich zwei Platten an beiden Enden des Strahlungskanals, eine obere Platte mit der Fläche AE, im weiteren als Erdplatte bezeichnet, die auf 30 °C erwärmt wird, und eine gekühlte Platte am Boden (Atmosphärenplatte, Atm-Platte), die auf -11,4 °C stabilisiert ist. Die Erdplatte befindet sich in einer Kuppel, die von außen mit warmen Wasser auf 30 °C erwärmt wird, wodurch Wärmeleitungsverluste weitgehend ausgeschlossen werden. Der Abstand der Platten beträgt 111 cm. Es werden keine zusätzlichen Lichtquellen im sichtbaren oder IR-Bereich verwendet, sondern nur die von den beiden Platten emittierte und mit den Gasen interagierende Strahlung untersucht (Abb. 1). Für weitere Details, siehe Harde & Schnell 2022 [1, 2].
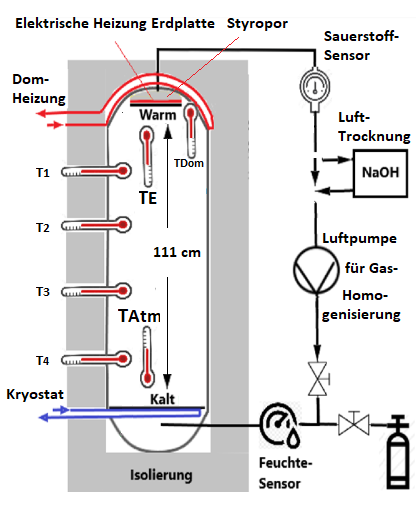
Abb. 1: Versuchsanordnung für die Messung mit Treibhausgasen.
Damit werden Bedingungen für den Strahlungsaustausch ähnlich dem Erde-Atmosphären-System (EASy) mit der wärmeren Erdoberfläche und der kälteren Atmosphäre simuliert. Es werden auch Probleme vermieden, die durch einen unpassenden Spektralbereich einer externen Quelle verursacht werden, durch die viel Abwärme im Behälter und an Fenstern erzeugt wird, die aber nur schlecht an die Absorptionsbanden der Treibhaus-Gase (TH-Gase) angepasst ist und hierdurch die Messempfindlichkeit deutlich verringert.
Für ein Probengas im Behälter ist die beheizte Erdplatte gleichzeitig IR-Strahlungsquelle und empfindlicher Detektor für die Rückstrahlung von TH-Gasen. Auf diese Weise wird die reine Strahlungswirkung der Gase als direkte Temperaturerhöhung ΔTE der Erdplatte oder alternativ, bei stabilisierter (konstanter) Temperatur TE, die Leistungseinsparung der Plattenheizung ΔHE bzw. die zugehörige Heizintensität ΔIH = ΔHE/AE gemessen.
Dieser Aufbau ermöglicht weitgehend, Konvektion oder Wärmeleitung zu eliminieren und damit den direkten Einfluss von TH-Gasen unter ähnlichen Bedingungen wie in der unteren Troposphäre reproduzierbar zu untersuchen. Eine spürbare Beeinflussung durch Wärmeleitung kann durch Kontrollexperimente mit Edelgasen ausgeschlossen werden [1, 2].
2. Einige physikalische Grundlagen
2.1 Spektrale Absorption und Emission
In guter Näherung kann angenommen werden, dass die Erdoberfläche, oder hier die geschwärzte Erdplatte und auch die Atm-Platte, als schwarze Körper mit einer Planck-Verteilung strahlen, die nur durch die Temperatur des Körpers bestimmt wird. Auf einer Wellenlängenskala erstreckt sich das jeweilige Spektrum von etwa 4 µm bis in den cm-Bereich, in reziproken Wellenlängen 1/λ als Wellenzahlen (Einheiten: cm-1) von 10 bis 2.500 cm-1.
a) Strahlung von Warm nach Kalt (Vorwärts-Strahlung)
Abb. 2 zeigt das emittierte Spektrum der Erdplatte für TE = 30 °C (Rot). Anders als Stickstoff, Sauerstoff oder Edelgase können die TH-Gase Strahlung in diesem Spektralbereich absorbieren, aber bei ausreichender Temperatur des Gases auch emittieren. Für CO2 z. B. findet die dominierende Wechselwirkung auf den Rotations-Vibrations-Übergängen der Knickschwingung um 670 cm-1 statt (15 µm).

Abb. 2: Strahlungs-Transfer-Rechnung für 20 % CO2 in trockener Luft über 111 cm bei einem Temperaturgradienten von -0,373 °C/cm. Schwarzkörperstrahlung der Platte PE (TE = 30 °C) (Rot Gelb), durchgelassene spektrale Intensität (Dunkelrot u. Grau).
Aufgrund dieser Wechselwirkung zeigt sich als Nettoeffekt, dass die spektrale Intensität auf dem Weg von der warmen zur kalten Platte über die Absorptionsbande kontinuierlich abgeschwächt wird (Gelb), in den Flanken der Bande durch schwächere Linien entsprechend geringere Verluste erleidet (Grau), dabei aber längst nicht so stark abklingt, wie für eine reine Absorption über diese Länge zu erwarten wäre. Für 20% CO2 in trockener Luft ergibt sich dabei für die von der Erd-Platte emittierte Strahlung mit einer Gesamtintensität von 479 W/m2 (Integral über spektrale Intensität) über den Ausbreitungsweg von 111 cm zur Atm-Platte und bei einem Temperaturgefälle von 0,373 °C/cm (TE = 30 °C, TA = -11,4 °C) eine Abschwächung um 25,1 W/m2 oder relativ um 5,2 %. Absorption allein würde zu einer Abnahme um 73,6 W/m2 (15,2 %) führen.
Solch eine Rechnung erfolgt in der Form, dass die Absorption und Emission in jeweils dünnen Schichten von Δz = 1 cm ermittelt wird (Strahlungstransfer-(ST)-Rechnung, Schwarzschild-Gleichung). Für jede Schicht müssen hierzu die spektralen Änderungen, in diesem Fall von mehr als 12.000 Linien, mit ihren druck- und temperaturabhängigen Linienbreiten und Absorptions- bzw. Emissionskoeffizienten berechnet werden, um schließlich nach 111 Berechnungsschritten die transmittierte Intensität zu erhalten.
Dieser Strahlungstransfer entspricht Verhältnissen, wie sie von Satelliten-Messungen bekannt sind, die die ins All abgegebene Strahlung aufzeichnen und die durch den typischen Trichter um 670 cm-1 gekennzeichnet sind. In diesem Spektralbereich wird die einfallende Strahlung unter den gegebenen Bedingungen, in der Atmosphäre ebenso wie hier im Laborexperiment, fast vollständig absorbiert, und die beobachtete Intensität resultiert nur aus der thermischen Emission des Gases, das in größeren Höhen oder hier in der Nähe der Atm-Platte bei reduzierter Temperatur entsprechend schwächer strahlt. In diesem Fall absorbiert CO2 von der Strahlung der PE-Platte zunächst 73,6 W/m2 und emittiert wieder 48,5 W/m2, während im Gasvolumen eine Differenz von 25,1 W/m2 verbleibt.
b) Strahlung von Kalt nach Warm (Rückstrahlung)
Für eine vollständige Strahlungsbilanz ist aber auch die Strahlung in Rückwärtsrichtung von der Atm-Platte zur Erdplatte zu berücksichtigen, die für die hier durchgeführten Untersuchungen zum Treibhaus-Effekt (TH-Effekt) von besonderem Interesse ist. Dies ist in Abb. 3 dargestellt.
Aufgrund des positiven Temperaturgradienten über den Ausbreitungsweg wird jetzt beim Durchqueren der Gasschicht die Strahlung mit einer Anfangsintensität von 266 W/m2 (Blaue Linie, TA = −11,4 °C) um 24,2 W/m2 ‘verstärkt‘, die dem Gasvolumen entnommen werden. Die Eigenstrahlung des Gases in Richtung der wärmeren Erdplatte kann klar als Peak um 670 cm−1 (Dunkelrot mit grauen Flanken) über dem breiteren Spektrum der Atmosphärenplatte identifiziert werden. Auf den stärkeren Linien in der Bandenmitte erreicht die Gasemission bereits volle Sättigung mit spektralen Intensitäten vergleichbar zu der spektralen Emission der Erdplatte (rote Linie) in diesem Spektralbereich. Die Emission auf den schwächeren Linien ist in Grau dargestellt.
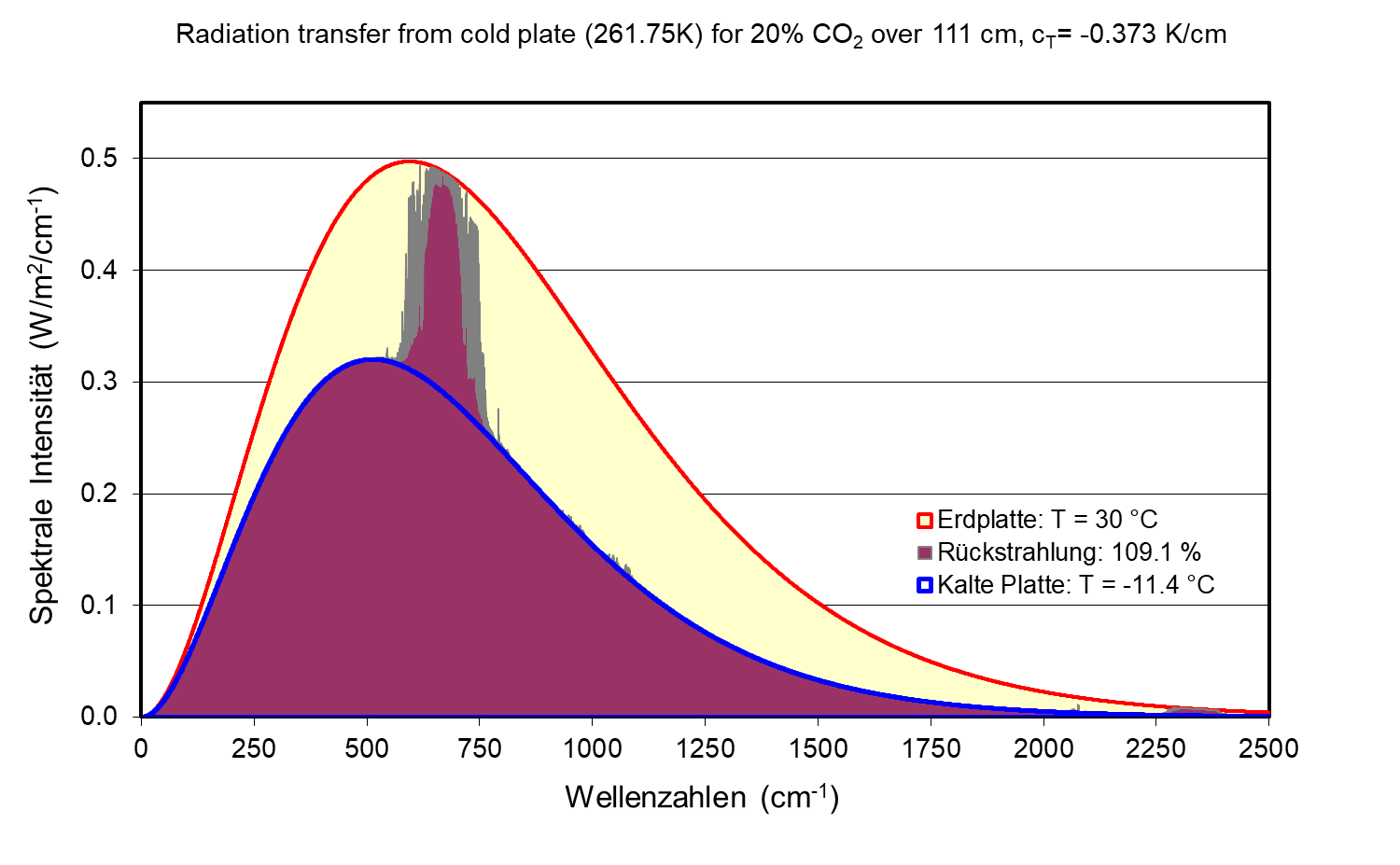
Abb. 3: Strahlungs-Transfer-Rechnung für 20 % CO2 in Luft über 111 cm für einen Temperaturanstieg von 0,373 °C/cm: Rückstrahlung von Atmosphärenplatte und Gas (Dunkelrot und Grau), Strahlung nur von Atmosphärenplatte (Blaue Linie) und spektrale Intensität der Erdplatte (Rot-Gelb).
Die erhöhte Rückstrahlung ist nahezu identisch mit den Verlusten in Vorwärtsrichtung, so dass innerhalb der Beobachtungsgenauigkeit die Gesamtbilanz aus Absorption und Emission des Gases Null ist.
Dies ist ein wichtiger Aspekt, der gegen die Messung der Gastemperatur zum Nachweis des TH-Effektes spricht. Dagegen kann mit dem vorgestellten Aufbau die Rückstrahlung der TH-Gase durchaus als Temperaturanstieg ΔTE der Erdplatte klar erfasst werden.
3. Einwände gegen den Treibhauseffekt
3.1 Molekülstöße
Einer der häufigsten Einwände gegen den TH-Effekt ist, dass TH-Gase nicht in der unteren Atmosphäre emittieren würden, während sie in der Tropopause und Stratosphäre gute Emittenten sind. Als Erklärung geben Kritiker an, dass in der unteren Troposphäre Kollisionsprozesse mit Stickstoff und Sauerstoff jede spontane Emission unterdrücken und die absorbierte Energie nur in kinetische Energie und damit in Wärme umgewandelt wird.
Leider wird bei dieser Interpretation übersehen, dass die typischen Stoßraten von mehreren GHz, wie sie in der unteren Atmosphäre beobachtet werden, sich in einer Höhe von 11 km nur um den Faktor 4–5 verringern und daher immer noch etwa 100 Millionen Mal größer als die spontane Übergangsrate von etwa 1 Hz auf der CO2-Biegeschwingung sind. Wenn eine solche Interpretation wahr wäre, gäbe es auch keine Emission in der höheren Atmosphäre.
Vielmehr kommt es auch ohne vorherige Absorption eines IR-Lichtquants zu einer kontinuierlichen Emission, da neben superelastischen Stößen (stoßbedingte Übergänge von einem höheren zu einem tieferen molekularen Zustand) auch inelastische Stöße stattfinden, die dem Gasgemisch kinetische Energie entziehen und diese wieder umwandeln, um die TH-Gasmoleküle anzuregen (Harde 2013 [3], Unterabschnitt 2.3). Dadurch werden tiefer liegende Energieniveaus bei ausreichender thermischer Energie kontinuierlich neu besetzt und die spontane Emission erfolgt weitgehend unabhängig – parallel zu den superelastischen Stößen – als thermische Hintergrundstrahlung (Harde 2013 [3], Abs. 2.5). Diese Emission wird durch die Lufttemperatur vorgegeben und ist der Hauptgrund dafür, dass mit zunehmender Höhe die Strahlungsintensität deutlich abnimmt. So beträgt sie in 11 km Höhe für CO2 beispielsweise nur 12 % der Intensität, die in einer 100 m dicken Gasschicht in Bodennähe beobachtet wird.
Stöße (adiabatisch und diabatisch) machen sich vor allem als spektrale Verbreitung der Linien bemerkbar. Aber auf diesen Frequenzen und über längere Weglängen kann die Strahlung die gleiche Stärke wie ein Schwarzkörperstrahler erreichen, und im thermischen Gleichgewicht wird dies hauptsächlich durch die Gastemperatur TG gesteuert.
Würden TH-Gase in der unteren Troposphäre nur absorbieren, nicht aber emittieren, würde nicht nur die Rückstrahlung, sondern auch die Aufwärtsstrahlung und damit ein effizienter Wärmetransport nach oben unterdrückt werden. Als Konsequenz könnte sich noch mehr Wärme in den unteren Schichten ansammeln und die Oberfläche stärker aufheizen als jede Rückstrahlung.
3.2 Zweiter Hauptsatz der Thermodynamik
Ein weiterer Einwand ist, dass die Strahlung eines kühleren Körpers nicht von einem wärmeren Körper absorbiert werden kann, da dies gegen den 2. Hauptsatz der Thermodynamik verstoßen würde. Wie bereits in Teil 1 gezeigt [4], wird dies durch die Messungen mit veränderter Temperatur und Oberfläche der kühleren Platte, ebenso wie durch den Demonstrationsversuch mit der Zwischenplatte im Strahlengang klar widerlegt.
Auch Messungen mit dem neuen Aufbau, bei denen die Temperatur der Atm-Platte sukzessive erhöht und die verringerte Heizintensität gemessen wird, bestätigen eindeutig den „gleichzeitigen doppelten Wärmeaustausch durch Strahlung“ (Clausius). In einem geschlossenen System „erfährt der kältere Körper einen Wärmeanstieg auf Kosten des wärmeren Körpers, der wiederum eine langsamere Abkühlungsrate erfährt“. In einem offenen System mit externer Heizung führt die Rückstrahlung des kälteren Körpers klar zu einer höheren Temperatur des wärmeren Körpers als ohne diese Rückstrahlung.
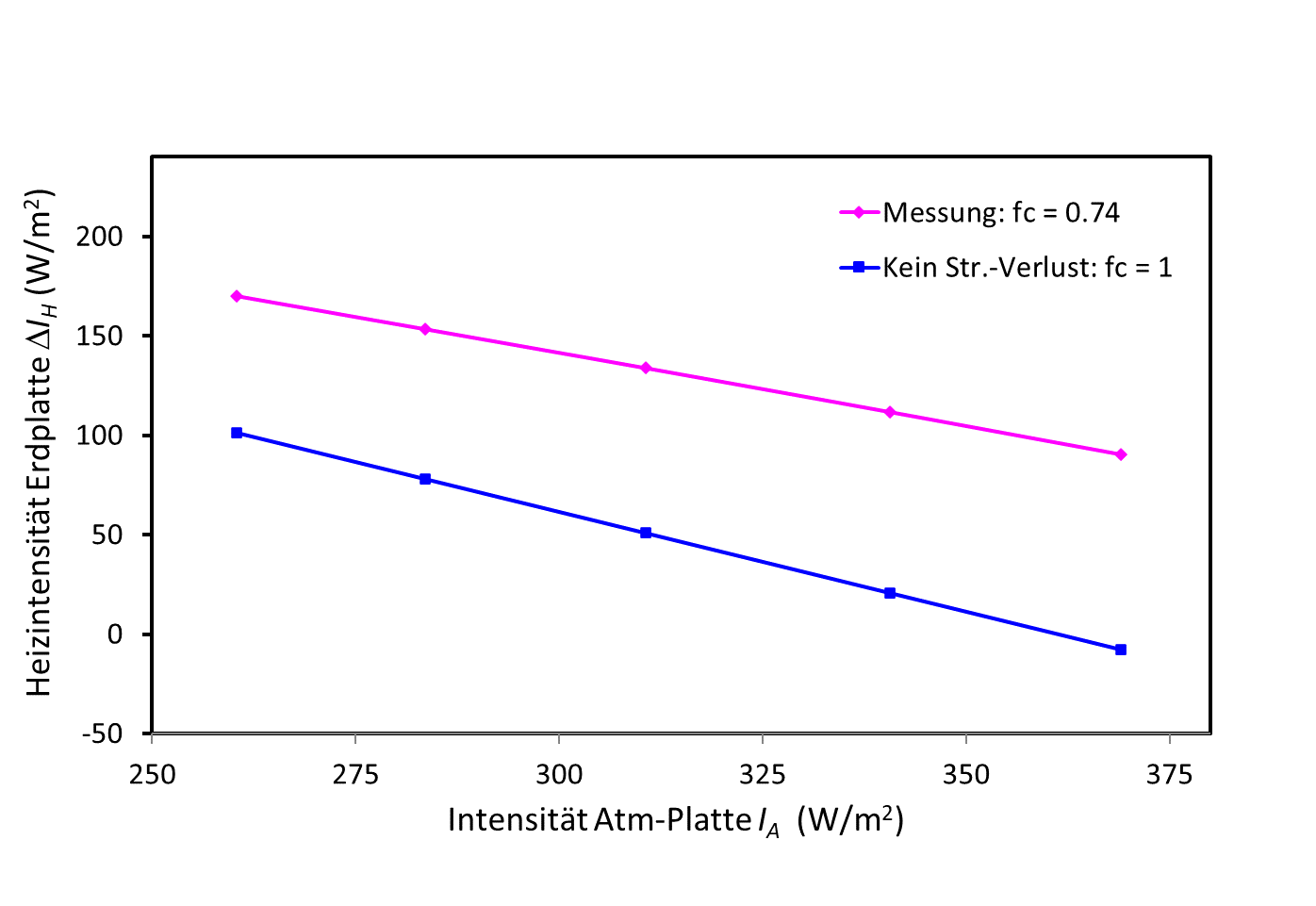
Abb. 4: Gemessene Heizintensität der Erdplatte für eine feste Temperatur TE = 30 °C als Funktion der Strahlungsintensität IA der Atm-Platte (Magenta Rhomben). Ebenfalls aufgetragen ist die theoretische Heizintensität für 100 %-ge Strahlungsübertragung (Blaue Quadrate).
Abb. 4 zeigt die Abnahme der Heizintensität ΔIH, wenn die Temperatur der Atm-Platte von -12,9 auf + 10,9 °C schrittweise erhöht wird. Bei diesen Temperaturerhöhungen steigt zunächst auch die Temperatur der Erdplatte an, was durch eine Verringerung der Heizintensität ausgeglichen wird, bis TE wieder 30 °C beträgt. Auf der Abszisse wird nicht die Temperatur, sondern die Strahlungsintensität IA der Atm-Platte (Magenta) gemäß der Stefan-Boltzmann-Gleichung (ε = 1) aufgetragen, wodurch eine Korrelation von Heiz- mit Strahlungsleistung ermöglicht wird. Der lineare Verlauf bestätigt einen Wärmetransport fast ausschließlich durch Strahlungstransfer entsprechend dem Stefan-Boltzmann-Gesetz, wobei Konvektion (durch die senkrechte Aufstellung) und Wärmeleitungsverluste (durch den beheizten Dom) weitgehend ausgeschlossen werden.
Mit einer solchen Messung lassen sich auch die Verluste beim Strahlungsaustausch zwischen Erd- und Atm-Platte direkt bestimmen. Im Idealfall, wenn die Heizintensität nur von der Rückstrahlung der Atm-Platte abhängen würde, müsste der Anstieg der Geraden fC = 1 sein. Gemessen wird aber ein Anstieg, ein Transmissionsgrad fC von 0,74, wodurch nachgewiesen wird, dass die Rückstrahlung nicht nur von der kalten Atm-Platte, sondern auch von der wärmeren Wand des Strahlungskanals verursacht wird. Das ist ein grundsätzliches Problem bei Strahlungskanälen, worauf schon im ersten Teil hingewiesen wurde [4].
Zum Vergleich ist der theoretische Verlauf mit dem Anstieg fC = 1 dargestellt (Blau), wenn es keine Strahlungsverluste gäbe. Gleichzeitig liefert die reduzierte Heizleistung bei einer beobachteten Temperaturerhöhung eine Eichung für die Temperaturempfindlichkeit der Erdplatte mit λE = 0,083 °C/W⋅m2.
4. Messungen mit Treibhausgasen
Es wurden die TH-Gase CO2, CH4 und N2O über einen weiten Bereich mit Konzentrationsänderungen bis zum 16-fachen der Ausgangskonzentration untersucht. Unsere Messungen zeigen eine deutliche Reaktion auf die TH-Gase, aber auch eine starke Sättigung im Temperaturanstieg mit zunehmender Konzentration. Und sie stimmen hervorragend mit detaillierten Strahlungstransfer-(ST)-Rechnungen überein.
4.1 CO2-Messungen
Abb. 5a zeigt den gemessenen Temperaturanstieg ΔTE an der Erdplatte als Funktion der CO2-Konzentration in trockener Luft. Die Konzentration wurde schrittweise von 1,25 % auf 20 % erhöht (Blaue Rauten).
Als direkter Vergleich ist der berechnete Temperaturanstieg ΔTC = λE⋅fCO2⋅ΔICO2 (Magenta-Quadrate) aufgetragen, basierend auf einer ST-Rechnung der CO2-Rückstrahlung ΔICO2 (Grüne Dreiecke), multipliziert mit einem Kalibrierungsfaktor, dem Transmissionsgrad fCO2 der von PW absorbierten Strahlung, und der separat gemessenen Temperaturempfindlichkeit λE der Erdplatte (siehe 3.3.2)
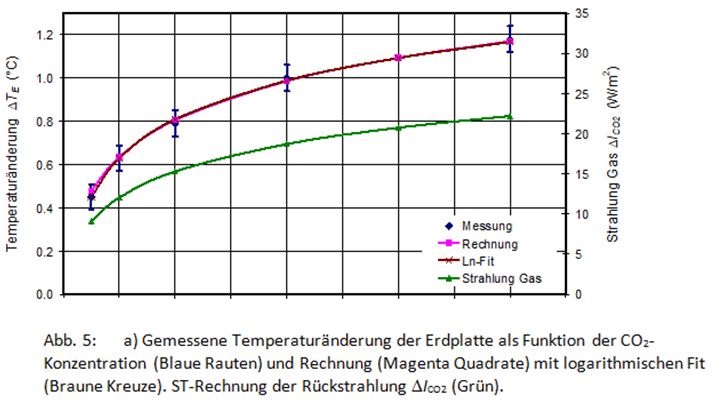
Abb. 5: a) Gemessene Temperaturänderung der Erdplatte als Funktion der CO2-Konzentration (Blaue Rauten) und Rechnung (Magenta Quadrate) mit logarithmischen Fit (Braune Kreuze). ST-Rechnung der Rückstrahlung ΔICO2 (Grün).
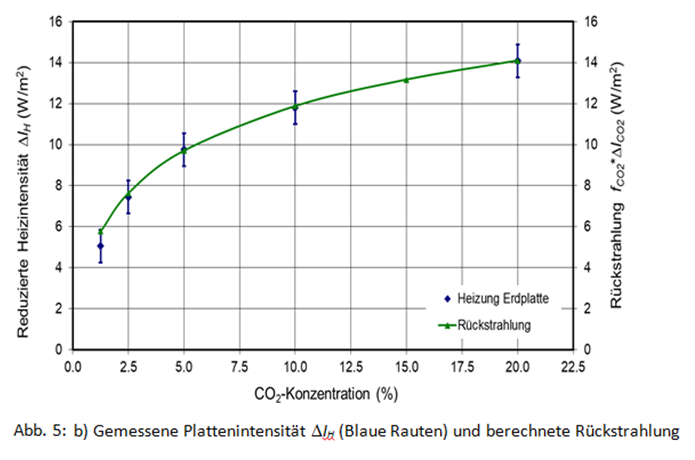
b) Gemessene Plattenintensität ΔIH (Blaue Rauten) und berechnete Rückstrahlung
unter Berücksichtigung der Strahlungsverluste mit fCO2⋅ΔICO2 für fCO2 = 0,59 (Grün).
Messung und Berechnung werden gut durch eine logarithmische Darstellung der Form als Funktion der Konzentration CCO2 in trockener Luft dargestellt (Braune Kreuze). Daraus leitet sich ein CO2-Strahlungsantrieb bei Verdopplung der CO2-Konzentration von ΔF2xCO2 = 3,7 W/m2 ab.
![]()
Eine unabhängige Messmethode zur Erfassung der Rückstrahlung ergibt sich, wenn mit steigender CO2-Konzentration die PE-Platte auf 30 °C stabilisiert und die eingesparte Heizintensität ΔIH, wie in Kap. 3.2 beschrieben, ermittelt wird.
Abb. 5b zeigt die eingesparte Heizintensität ΔIH für die Erdplatte (blaue Rauten), die erforderlich ist, um mit steigender CO2-Konzentration diese Platte auf 30 °C zu stabilisieren. Die eingesparte Heizintensität ΔIH kann gut durch die berechnete Rückstrahlung ΔICO2 bei einem Transmissionsgrad von fCO2 = 59 % reproduziert werden (Grün). Der Anteil fCO2 ergibt sich aus einer Anpassung an die eingesparte Heizintensität ΔIH. Aufgrund der volumenförmigen Absorption und Abstrahlung unterscheidet sich dieser Transmissionsfaktor leicht für die verschiedenen Gase und auch von dem Wert fC, der die Übertragungseigenschaften des Strahlungskanals ohne TH-Gase charakterisiert.
4.2 CH4-Messung
Messungen für CH4 wurden bei Konzentrationsänderungen von 1,25 bis 10 % in trockener Luft durchgeführt (Abb. 6). Der beobachtete Temperaturanstieg ΔTE der Erdplatte als Funktion der CH4-Konzentration (blaue Rauten) zeigt erneut eine hervorragende Übereinstimmung mit dem berechneten Temperaturanstieg (Magenta Quadrate) basierend auf der berechneten Rückstrahlung ΔICH4 (grüne Dreiecke). Mit Ausnahme der niedrigsten Konzentration weist auch dieses TH-Gas bei diesen Konzentrationsniveaus eine starke Sättigung auf und kann recht gut durch eine logarithmische Kurve (braune Kreuze) mit einem Strahlungsantrieb bei verdoppelter CH4-Konzentration von ΔF2xCH4 = 2,75 W/m2 dargestellt werden. Unter ansonsten vergleichbaren Bedingungen sind dies nur 74 % des CO2-Antriebs. Obwohl die atmosphärische Konzentration von CH4 mit 1,8 ppm mehr als 200-mal kleiner als die von CO2 ist, zeigt auch CH4 über den optischen Weg, der proportional zur Konzentration x Ausbreitungslänge ist, eine stärkere Sättigung in der Atmosphäre (siehe auch: http://hharde.de/climate %20c.htm).
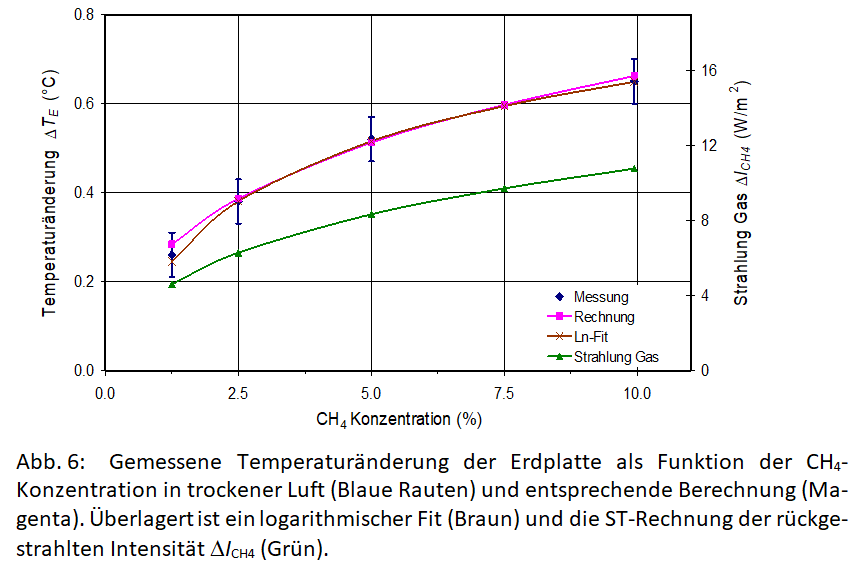
Abb. 6: Gemessene Temperaturänderung der Erdplatte als Funktion der CH4-Konzentration in trockener Luft (Blaue Rauten) und entsprechende Berechnung (Magenta). Überlagert ist ein logarithmischer Fit (Braun) und die ST-Rechnung der rückgestrahlten Intensität ΔICH4 (Grün).
4.3 N2O-Messung
Die N2O-Messungen wurden für Konzentrationen von 1,25 % bis 15 % durchgeführt (Abb. 7).
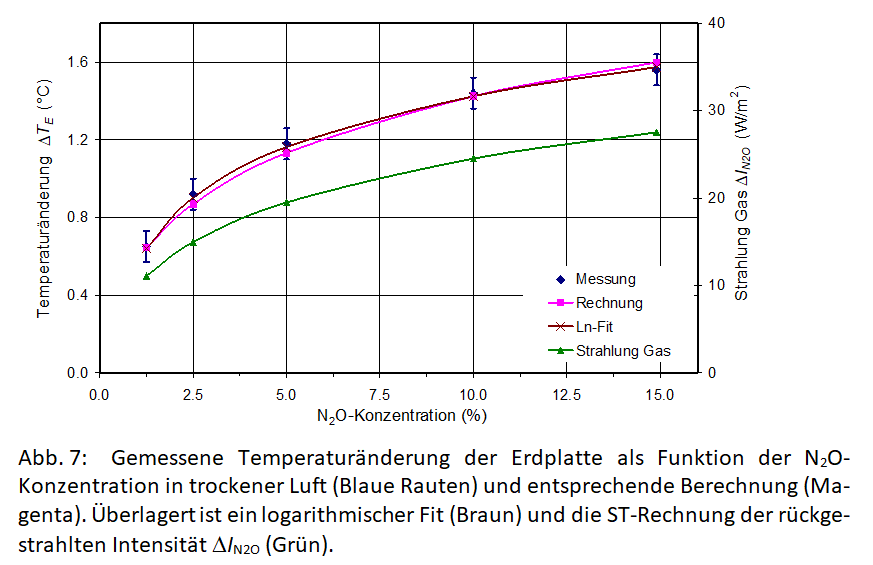
Abb. 7: Gemessene Temperaturänderung der Erdplatte als Funktion der N2O-Konzentration in trockener Luft (Blaue Rauten) und entsprechende Berechnung (Magenta). Überlagert ist ein logarithmischer Fit (Braun) und die ST-Rechnung der rückgestrahlten Intensität ΔIN2O (Grün).
Die gemessene Temperaturänderung ΔTE der Erdplatte (blaue Rauten) lässt sich wiederum für ansteigende N2O-Konzentration gut durch die berechnete Änderung ΔTC = λE⋅fN2O⋅ΔIN2O (Magenta Quadrate) reproduzieren. Die berechnete N2O-Emission ΔIN2O wird durch grüne Dreiecke wiedergegeben. Bei Anpassung der gemessenen Temperatur durch eine logarithmische Kurve (braune Kreuze) ergibt sich ein N2O-Strahlungsantrieb bei doppelter Konzentration von ΔF2xN2O = 5,0 W/m2. Dies ist 35 % größer als der CO2-Strahlungsantrieb.
5. Diskussion der Ergebnisse
5.1 Unterschiede zur Atmosphäre
Der vorgestellte Versuchsaufbau hat sich als geeignet erwiesen, den atmosphärischen TH-Effekt nachzuweisen und im Labor zu demonstrieren. Obwohl die Weglänge durch die Atmosphäre etwa um den Faktor 80.000 größer ist als die Messkammer, wird dies durch eine 500-fach höhere Konzentration für CO2 und eine 50.000-fach höhere CH4-Konzentration teilweise kompensiert und für N2O mit einer fast 500.000-mal höheren Konzentration im Vergleich zu den Meeresspiegelwerten sogar deutlich überkompensiert. Nicht so sehr die absoluten Werte sind dabei relevant, wichtiger ist der optische Weg als Produkt von Absorptionskoeffizient und Weglänge.
Andererseits ist der Temperaturgradient (Lapse-Rate) über die Troposphäre mit 6,5 °C/km 5.700-mal kleiner als in dem hier verwendeten Aufbau, während die absolute Temperaturdifferenz fast vergleichbar ist.
Am wichtigsten für den Nachweis des TH-Effektes und der Rückstrahlung von IR-aktiven Gasen ist jedoch deren Emission bei gleichzeitigen Stoßprozessen und dies unter Bedingungen, wie sie in der unteren Troposphäre anzutreffen sind. Die Experimente bestätigen damit definitiv, dass TH-Gase auf ihren Übergängen strahlen und innerhalb einer optisch dicken Schicht sogar vergleichbar zu einem Schwarzkörperstrahler mit gleicher Temperatur wie das Gas emittieren.
Unter realen atmosphärischen Bedingungen wird die Rückstrahlung der TH-Gase durch die spektral viel breitere Strahlung von Wolken überlagert, die in erster Näherung als graue Emitter mit einer durch ihre Unterseite gegebenen Temperatur beschrieben werden können. In den mit den TH-Gasen durchgeführten Experimenten werden Wolken durch die Atm-Platte und Kanalwände ersetzt. Ihre Strahlung ändert sich stark mit der Temperatur TA der Atm-Platte und simuliert auf diese Weise den Einfluss von Wolken in unterschiedlichen Höhen. Dies bestimmt aber auch die Größe des TH-Gasbeitrags, der vom Temperaturunterschied zwischen den Platten und damit von der Temperaturdifferenz abhängt. Auf die Atmosphäre übertragen bedeutet dies, dass bei Wolken die Rückstrahlung größer ist als bei klarem Himmel, der relative Beitrag durch TH-Gase jedoch abnimmt.
5.2 Reproduzierbarkeit und Genauigkeit
Die Reproduzierbarkeit der Messungen hängt stark von den Gleichgewichtsbedingungen des Aufbaus vor dem Befüllen der Messkammer mit dem TH-Gas ab, und dies gilt auch für die weitere Aufzeichnung von Daten. Die Temperaturanzeige ist auf ±0,13 °C begrenzt und bestimmt somit wesentlich die Genauigkeit der Messungen. Auch die elektrische Plattenheizung wird durch die Temperaturablesung beeinflusst, da jede Anfangs- und Endaufzeichnung zur Ermittlung der Differenz ΔHE zwei Temperaturmessungen erfordert. Dies ist der Hauptgrund für kleinere Abweichungen von einem Messdurchlauf zum nächsten. Zusätzliche Störungen gehen auf geringfügige Schwankungen der Raumtemperatur zurück, die innerhalb von ±0,2 °C geregelt werden kann.
Der Fehler für eine Einzelmessung der Temperaturänderung ΔTE und der reduzierten Heizleistung ΔHE wird bei den niedrigeren Konzentrationen auf ±20 % und bei den höheren Konzentrationen auf etwa ±10 % geschätzt. Die Gesamtgenauigkeit wird jedoch durch mehrmaliges Wiederholen der Messungen weiter verbessert. Alle Daten stellen das Mittel aus 5 Durchläufen dar. Dies ermöglicht es, den allgemeinen Trend einer Serie innerhalb von ±5 % zu bestimmen.
5.3 Vergleich mit der Literatur
Es zeigt sich für alle drei Gase eine gute Übereinstimmung zwischen Messung und Berechnung, sowohl für die Temperaturdaten als auch für die Plattenheizung. Insbesondere die zunehmende Sättigung und die charakteristische Abflachung mit steigender Gaskonzentration werden durch die Berechnungen gut bestätigt und schließen einen größeren Einfluss durch Wärmeleitung aus. Gleichzeitig zeigen diese Untersuchungen die nur geringe weitere Auswirkung auf die globale Erwärmung bei steigenden Treibhausgaskonzentrationen.
Während sich die Übereinstimmung in den Absolutwerten von gemessenen und berechneten Daten z.T. daraus erklärt, dass zur Ermittlung der Transmissionsgrade fGas – und damit für die entsprechende Skalierung der gemessenen Rückstrahlung und der Temperaturdaten – die Rechnungen als Referenz herangezogen werden, stellt die nahezu exakte Übereinstimmung des abgeleiteten Strahlungsantriebs für CO2 mit ΔF2xCO2 = 3,70 W/m2 eher eine zufällige Übereinstimmung mit der Literatur dar (siehe AR6 [5]), da die Messungen hier unter deutlich anderen Bedingungen durchgeführt wurden.
Dennoch ermöglicht dies einen direkten Vergleich untereinander, hierzu müssen allerdings die verschiedenen Auswirkungen berücksichtigt werden, wie z. B. eine sich ändernde Druckverbreiterung der Absorptionslinien über die Weglänge in der Atmosphäre, die Interferenz mit anderen TH-Gasen wie Wasserdampf, die unterschiedliche Bodentemperatur, und die sich ändernde Rückstrahlung mit unterschiedlicher Wolkenhöhe, Bewölkung und Emissionsgraden. Daraus lässt sich ein Strahlungsantrieb von ΔF2xCO2 = 3,4 W/m2 berechnen, und zusammen mit einer Planck-Sensitivität von λP = 0,31 °C/(W/m2) (siehe AR6 [5]) ergibt dies eine Basis-Gleichgewichts-Klimasensitivität (Temperaturanstieg bei verdoppelter CO2-Konzentration, ohne Rückkopplungen) von ECSB = λP⋅ΔF2xCO2 = 1,05 °C. Dieses Ergebnis stimmt hervorragend mit dem Coupled Model Intercomparison Project Phase 5 (CMIP5) überein.
Allerdings zeigen eigene Berechnungen unter Einbeziehung von Rückkopplungen, dass Wasserdampf im Gegensatz zu den Annahmen des IPCC nur noch zu einer marginalen positiven Rückkopplung beiträgt und die Verdunstung an der Erdoberfläche sogar zu einer deutlichen weiteren Reduzierung der Klimasensitivität auf nur noch ECS = 0,68 °C führt (Harde 2017 [6], Harde 2022 [7]). Dies ist weniger als ein Viertel des IPCC-Wertes mit ECS = 3 °C (AR6 [5]) und 5,4-mal kleiner als der Mittelwert von CMIP6 mit ECS = 3,78 °C.
Entsprechende Werte für CH4 und N2O können nur indirekt mit der Literatur verglichen werden, da hierfür nur Werte für den ppb-Bereich (parts per billion) angegeben werden, bevor Sättigungseffekte auftreten. Dennoch erlauben ihre relativen Werte zu CO2 durchaus eine Abschätzung ihrer Beiträge zur globalen Erwärmung, die für CH4 nicht mehr als 2 % und für N2O weniger als 1 % betragen.
Eine faustdicke Überraschung ist Methan, das tatsächlich einen geringeren Strahlungsantrieb als CO2 hat und angesichts seiner derzeitigen Konzentration von nur 1,89 ppm eindeutig kein Super-Treibhausgas ist, das Anlass zur Sorge geben sollte, wie uns manche Medien oder Klimaforscher glauben machen wollen.
6. Zusammenfassung
Die vorgestellten Messungen und Berechnungen bestätigen eindeutig die Existenz eines atmosphärischen TH-Effektes und zeigen entgegen dem oft falsch interpretierten zweiten Hauptsatz der Thermodynamik, dass ein wärmerer Körper durch die Strahlung eines kälteren Körpers, hier die Strahlung der gekühlten Platte und/oder eines TH-Gases, weiter erwärmt werden kann (siehe auch EIKE, Teil 1 [4]).
Sie bestätigen auch, dass TH-Gase unter Bedingungen, wie sie in der unteren Atmosphäre herrschen, auch IR-Strahlung in „Rückwärtsrichtung“ aussenden. Gleichzeitig offenbaren die theoretischen Untersuchungen die prinzipiellen Schwierigkeiten, den TH-Effekt als steigende Temperatur des Gases zu messen. Solche Versuche zeigen hauptsächlich eine Erwärmung durch Absorption von NIR oder IR-Licht über die Gefäßwände, während nur zu einem geringeren Grad Absorption durch die Gase erfolgt.
Solche Experimente übersehen oft auch, dass der Treibhauseffekt hauptsächlich das Ergebnis einer Temperaturdifferenz über den Ausbreitungsweg der Strahlung und damit der ‚Lapse-Rate‘ in der Atmosphäre ist.
Ein verminderter TH-Effekt bei reduzierter Temperaturdifferenz zwischen den Platten, wie dies analog auch durch Wolken in der Atmosphäre erfolgen kann, lässt sich klar nachweisen.
Unsere Ergebnisse zeigen nur einen geringen Einfluss von TH-Gasen auf die globale Erwärmung, die offensichtlich viel stärker von natürlichen Einflüssen wie dem solaren Strahlungsantrieb und Ozeanischen Oszillationen dominiert wird (siehe z. B. Connolly et al. 2021 [8]; Harde 2022 [7]). Es gibt also keinen Grund für Panik und Klimanotstand, vielmehr ist es höchste Zeit, zu einer konsolidierten Klimadiskussion zurückzukehren, die sich auf Fakten konzentriert und auch die Vorteile von Treibhausgasen einbezieht.
7. Referenzen
- H. Harde, M. Schnell, 2022: Verification of the Greenhouse Effect in the Laboratory, Science of Climate Change, Vol. 2.1, pp. 1-33, https://doi.org/10.53234/scc202203/10.
- H. Harde, M. Schnell, 2022: Nachweis des Treibhauseffekts im Labor, PDF-Datei
- H. Harde, 2013: Radiation and Heat Transfer in the Atmosphere: A Comprehensive Approach on a Molecular Basis, International Journal of Atmospheric Sciences (Open Access), vol. 2013, http://dx.doi.org/10.1155/2013/503727
- M. Schnell, H. Harde, 2024: Gibt es einen Atmosphärischen Treibhaus-Effekt? -Teil 1, EIKE 2024
- Sixth Assessment Report (AR6) of the IPCC, 2021: Climate Change 2021: The Physical Science Basis, Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change [Masson-Delmotte, V. et al. (eds.)]. Cambridge University Press.,
https://www.ipcc.ch/report/ar6/wg1/downloads/report/IPCC_AR6_WGI_TS.pdf - H. Harde, 2017: Radiation Transfer Calculations and Assessment of Global Warming by CO2, International Journal of Atmospheric Sciences, Volume 2017, Article ID 9251034, pp. 1-30, https://www.hindawi.com/journals/ijas/2017/9251034/, https://doi.org/10.1155/2017/9251034.
- H. Harde, 2022: How Much CO2 and the Sun Contribute to Global Warming: Comparison of Simulated Temperature Trends with Last Century Observations, Science of Climate Change, vol. 2, no 1, pp 105 -133, https://doi.org/10.53234/scc202206/10
- R. Connolly, W. Soon, M. Connolly, S. Baliunas, J. Berglund, C. J. Butler, R. G. Cionco, A. G. Elias, V. M. Fedorov, H. Harde, G. W. Henry, D. V. Hoyt, O. Humlum, D. R. Legates, S. Lüning, N. Scafetta, J.-E. Solheim, L. Szarka, H. van Loon, V. M. V. Herrera, R. C. Willson, H. Yan and W. Zhang, 2021: How much has the Sun influenced Northern Hemisphere temperature trends? An ongoing debate, Research in Astronomy and Astrophysics 2021 Vol. 21 No. 6, 131(68pp),
http://www.raa-journal.org/raa/index.php/raa/article/view/4906
Zur Sicherstellung sämtlicher Indizes und anderer evtl. Buchstabendarstellung zwischen Word und dieser Darstellung hier nochmal Gibt es einen Atmosphärischen Treibhauseffekt Teil 2 Vollständig