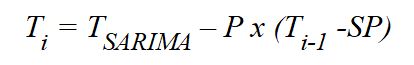Launen der Temperatur-Rückkopplung
Ist es wirklich das wärmste seit 125.000 Jahren, und wenn ja, was bedeutet das?
Chris Hall
Der Anlass für diesen Artikel waren die Behauptungen, dass der vorige Sommer der heißeste seit 125.000 Jahren war, nebst der atemlosen Angst, die damit verbunden war. Schon beim Überfliegen der Nachrichtenmeldungen wurde mir klar, dass diese Behauptung auf zwei wesentlichen Punkten beruht: der Annahme, dass das Klima sehr stabil ist und sich vor der jüngsten anthropogenen Beeinflussung nicht verändert hat, und dass die derzeitige Abweichung von der Mitteltemperatur so viele Standardabweichungen (Sigma) über dem erwarteten Wert liegt, dass sie in den letzten 125.000 Jahren unmöglich erreicht oder überschritten werden konnte.
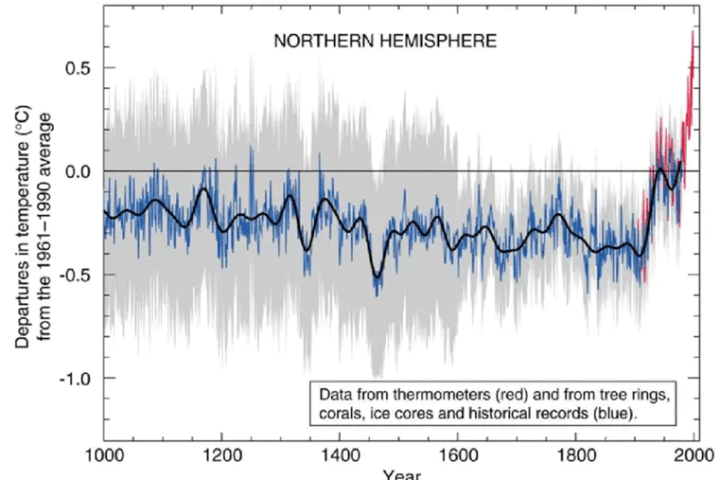
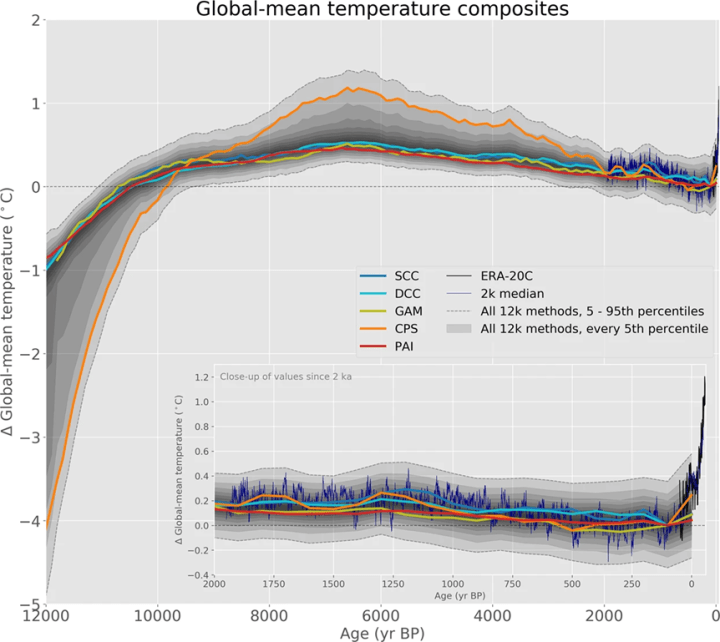
Die erste Annahme entspricht einer Paläotemperatur-Rekonstruktion im Stil des „Hockeysticks“, bei der die natürliche Temperaturschwankung im letzten Jahrtausend sehr gering ist. Es gibt mehrere Rekonstruktionen dieser Art, z. B. einige der flacheren Temp12k-Aufzeichnungen, sowie den klassischen Hockeystick (Abb. 1 und 2). Die zweite Annahme beruht auf dem Glauben, dass sich die statistischen Eigenschaften der paläoklimatischen Temperaturaufzeichnungen über einen sehr langen Zeitraum hinweg überhaupt nicht verändert haben.
Obwohl ich mich weder für die eine noch für die andere Paläotemperatur-Rekonstruktion aussprechen möchte, weise ich darauf hin, dass die 125.000 Jahre, die für unsere Rekordtemperaturen genannt werden, auf einem kleinen Taschenspielertrick beruhen. Wenn man sich die Temperaturaufzeichnungen des Wostok-Eiskerns auf der Paläoklima-Seite von wattsupwiththat (Abb. 3) ansieht, fällt die Temperatur, sobald man etwa 12.000 Jahre bis zum Beginn des Holozäns zurückgeht, drastisch in die Tiefen einer schweren Eiszeit ab, und erst wenn man etwa 125.000 Jahre in der Zeit zurückreist, bis man das warme Eem erreicht, kehrt man zur „Normalität“ zurück. In Wirklichkeit ist es also keine große Leistung, wärmer zu sein als der riesige Canyon des Eiszeitalters. Es stellt sich also die Frage, ob 2023 das heißeste Jahr und der August 2023 der heißeste Monat seit 12.000 Jahren war.
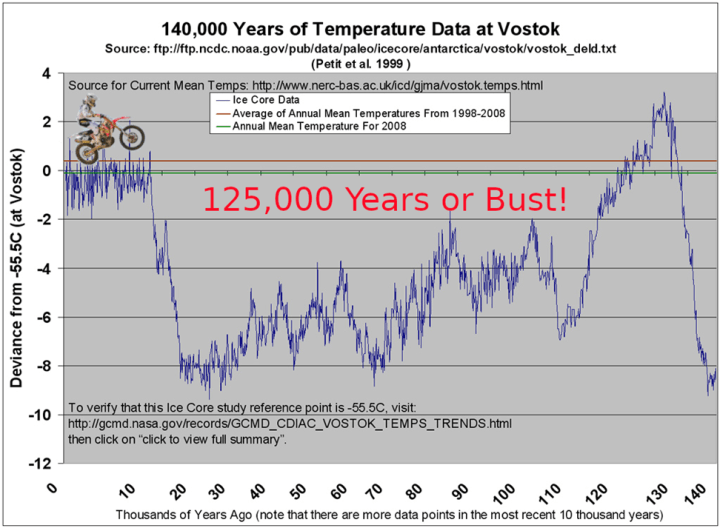
Abbildung 3: Leicht veränderte Rekonstruktion der Temperaturanomalie des Wostok-Eiskerns, entlehnt von der Paläoklima-Referenzseite von wattsupwiththat.
Für den Rest dieses Artikels werde ich den unwahrscheinlichen Fall annehmen, dass die Temperatur im Holozän extrem stabil war. Welche statistischen Eigenschaften hat dann die heutige instrumentelle Temperaturaufzeichnung, und was bedeutet das für die Behauptung von Rekordtemperaturen? Dies führt mich zu der Frage, was dies für die Rückkopplungs-Prozesse des Klimas bedeutet.
Globale monatliche Temperaturanomalien nach HadCRUT5: Das ist es, was wir haben
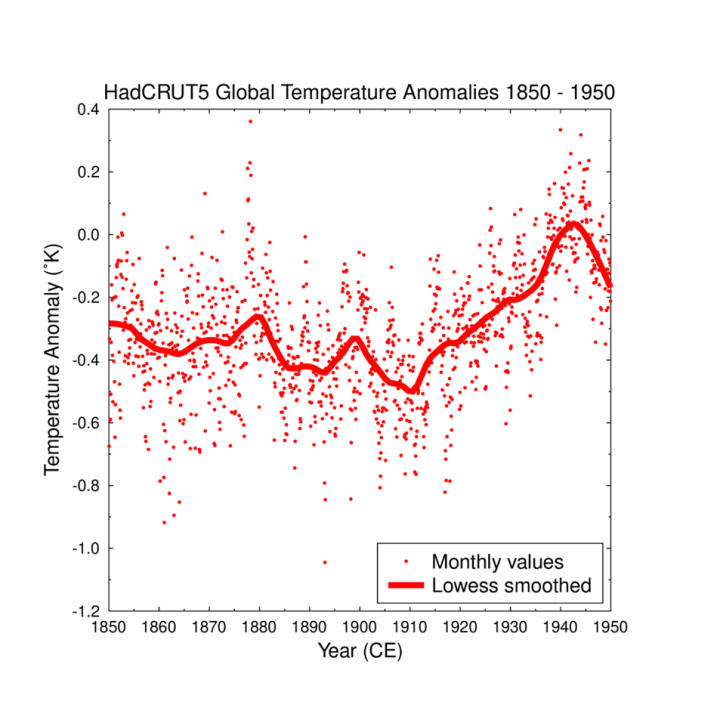
Ich beschloss, mir die offiziellen Temperaturaufzeichnungen aus einem Jahrhundert instrumenteller Daten anzusehen, das dem größten Teil des anthropogenen CO₂-Anstiegs vorausgeht, d. h. von 1850 bis 1950. Hierfür schien die globale monatliche HadCRUT5-Analyse eine vernünftige Wahl zu sein. Es gibt noch andere, aber sie sind hochgradig miteinander korreliert und basieren auf denselben Rohdaten, so wie sie sind. Dieser Datensatz ist in Abb. 4 dargestellt.
Der Mittelwert dieses Teils der Aufzeichnung beträgt -0,3078°C, was als Anomalie gegenüber einem späteren Teil der Aufzeichnung ausgedrückt wird, und die Standardabweichung beträgt 0,2066. Die Höchsttemperatur des gesamten globalen monatlichen Datensatzes stammt aus dem August 2023 mit einem Anomaliewert von 1,3520. Es zeigt sich also, dass der August über 8 Sigma über meinem Mittelwert von 1850 bis 1950 lag. Wahnsinn! Ich vermute, dass eine einfältige Extrapolation in die Vergangenheit nahelegen würde, dass wir diese sengende Temperatur während des Holozäns nicht überschritten hätten.
SARIMA-Bereich
Der nächste Abschnitt ist etwas umfangreich und kann von allen übersprungen werden, die sich nicht mit der Frage beschäftigen wollen, wie ich simulierte Temperaturaufzeichnungen auf der Grundlage der statistischen Eigenschaften der bestehenden Temperaturaufzeichnungen von 1850-1950 erstellt habe. Sie passt sich einem Modell an, das von einer Autokorrelation innerhalb der Aufzeichnung ausgeht. Die verwendeten Verfahren sind bei Aktienhändlern sehr beliebt, und die meisten der verwendeten Programme sind in der R-Bibliothek „forecast“ enthalten. Wenn Sie sich für solche Dinge nicht interessieren, können Sie diesen Abschnitt überspringen.
Und genau dem folgt diese Übersetzung. Es ist ein theoretischer Teil, dessen Ergebnisse unten beschrieben werden. Jeder an Theorie Interessierte dürfte der englischen Sprache mächtig genug sein, diese Passage im Original zu betrachten. A. d. Übers.
…
Steuerknöpfe: „hoch“ oder „niedrig“, das ist hier die Frage
Die sich aus der Modellierung der Temperaturzeitreihen ergebenden Residuen des weißen Rauschens sind das zufällige, chaotische Hintergrundrauschen des Klimas. Sie sind wahrscheinlich das Ergebnis von Vulkanen, ozeanischen Wirbeln, Sonnenaktivität, dem Ausgasen von Reisfeldern und dem chaotischen Flattern von manischen Schmetterlingen. Was auch immer Sie tun, es scheint, dass die Temperaturaufzeichnungen der Erde jeden Monat chaotisch um etwa 1/8 Grad Celsius auf und ab schwanken, und diese Schwankungen sind nicht autokorreliert und hängen nicht von der Jahreszeit ab. Wichtig ist, wie sich die beiden oben abgeleiteten statistischen Modelle über einen längeren Zeitraum hinweg verhalten.
In Abb. 6 zeige ich die Ergebnisse von zwei Simulationen, die über 1000 Jahre laufen. Bei dem in Abb. 5c gezeigten Modell handelt es sich um eine klassische Version einer „Random Walk“-Zeitreihe. Bei einem „Random Walk“ ist die Reihe nicht an einen bestimmten „Sollwert“ (SP) gebunden und kann munter hin und her wandern, nach oben oder unten oder hin und her oszillieren. Diese Art von Verhalten steht in engem Zusammenhang mit dem physikalischen Prozess der Diffusion, und die durchschnittliche Entfernung vom ursprünglichen Ausgangspunkt, der hier als Temperaturanomalie von Null angenommen wird, nimmt mit der Quadratwurzel der Zeit zu. Im Wesentlichen fehlt bei dieser Art von Zeitreihen jede Art von negativer Rückkopplung, die die Temperatur an einen bestimmten SP bindet. Dieses Verhalten ist unvereinbar mit Proxy-Temperaturaufzeichnungen, die angeblich zeigen, dass es seit Jahrhunderten oder Jahrtausenden keine signifikanten Temperaturveränderungen gibt.
Das in Abb. 5b gezeigte Modell ist jedoch perfekt für diejenigen, die behaupten, dass sich die globale Temperatur über einen längeren Zeitraum hinweg nicht wesentlich verändert hat. In diesem Fall oszilliert die Temperatur zwar um den Nullpunkt, aber ihre durchschnittliche Abweichung von diesem SP nimmt mit der Zeit nicht zu. Dies deutet darauf hin, dass es eine Reihe von negativen Rückkopplungen gibt, die die Reihe in der Nähe des SP halten. Auf diese Art von Zeitreihen werde ich noch näher eingehen.
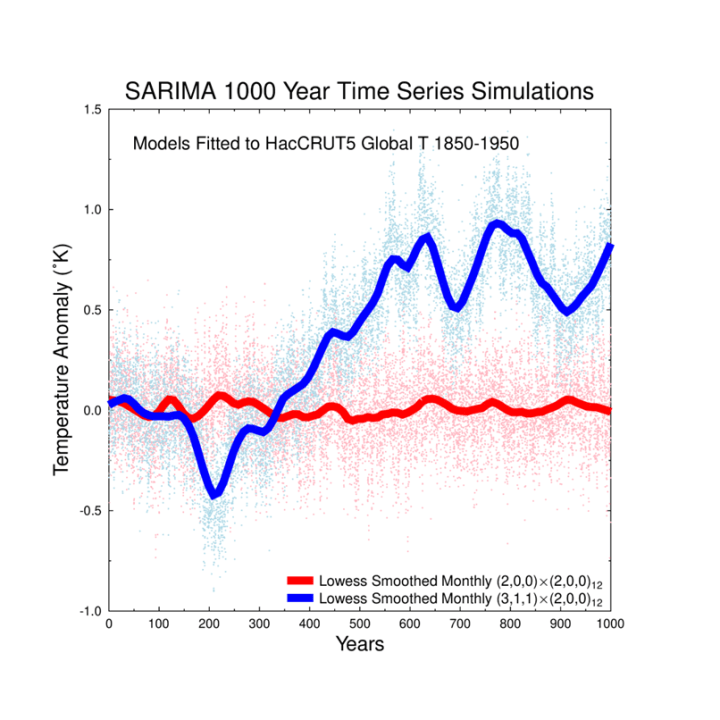
Abbildung 6: Typische SARIMA* simulierte 1000-Jahre-Temperaturzeitreihen für die beiden angepassten Modelle. Die Punkte stellen einzelne Monatswerte dar, und die dicken Linien sind die geglätteten Versionen der Zeitreihen nach Lowess. Das (2,0,0)x(2,0,0)12-Modell ist fest in der Nähe des Sollwerts 0 verankert, während das (3,1,1)x(2,0,0)12-Modell wie ein Random Walk wirkt, bei dem die Temperatur nicht an einen bestimmten Sollwert gebunden ist. Das letztgenannte Modell geht manchmal nach oben, manchmal nach unten und manchmal oszilliert es.
[*SARIMA = Seasonal Auto Regressive Integrated Moving Average]
Warum sollte man sich die Temperatur-Rückkopplung ansehen?
Ich weiß, was Sie sagen wollen: warum sollte man die Temperatur-Rückkopplung betrachten? Sicherlich wirken alle wichtigen Rückkopplungen auf die unzähligen Stellschrauben, die das Klima steuern, und nicht direkt auf die Temperatur. Und Sie hätten Recht – mit Ausnahme eines sehr wichtigen Reglers: CO₂. Im Falle von Kohlendioxid liegt die unmittelbare Klimaempfindlichkeit gegenüber einer Verdoppelung seiner Konzentration in der Atmosphäre irgendwo in der Nähe von 1,5°C. Die wirklich beängstigenden Folgen des Fahrens Ihres Geländewagens ergeben sich jedoch erst, wenn Sie die angenommene positive Rückkopplung des erhöhten Wasserdampfs in der Atmosphäre hinzurechnen, und diese positive Rückkopplung erfolgt über den Faktor Temperatur selbst. Erhöht man die Temperatur, entsteht mehr Wasserdampf, was zu einer höheren Temperatur führt. Senkt man sie, sinkt der Wasserdampfgehalt, wodurch es noch kühler wird. Da der Rückkopplungs-Prozess die Temperatur selbst ist, sollte jede Störung der Temperatur, sei es durch Rinderblähungen oder Schmetterlingsflügel, diese Rückkopplung aufweisen.
Um die Auswirkungen der Rückkopplung auf eine simulierte Temperaturaufzeichnung zu untersuchen, habe ich einen simulierten Proportional-Integral-Differential-Regler (PID) an das Ende der SARIMA-Simulation angehängt. Ich habe jahrzehntelang mit PID-Reglern gearbeitet, als ich versuchte, die Temperaturen von Laborproben auf einen bestimmten SP einzustellen, und zwar für Temperaturen zwischen 10°K und 1700°K. Obwohl diese Temperaturbereiche oft ein nicht-lineares Verhalten zeigen und man meinen könnte, dass ein inhärent lineares Regelsystem nicht funktionieren würde, zerlegt man in der Praxis die Temperaturbereiche in kleinere, nahezu lineare Bereiche, in denen der Regler recht gut funktioniert. Hier gehe ich davon aus, dass Temperaturabweichungen innerhalb weniger Grad von einer globalen Temperatur von etwa 288°K für einen PID-Regler „linear genug“ sind.
Der „P“-Wert ist ein negativer Rückkopplungsbetrag, der die Reaktion auf der Grundlage der aktuellen Abweichung vom gewünschten SP linear skaliert. Der „I“-Wert wird verwendet, um kleine Fehler auszugleichen, indem die Differenz zwischen der tatsächlichen Temperatur und dem SP über die Zeit integriert wird. Der Parameter „D“ wird verwendet, um große Überschwinger zu dämpfen, indem die Ableitung der Annäherung an den SP betrachtet wird. Da Temperaturableitungen oft verrauscht sind, wird der Parameter D bei vielen gut funktionierenden Systemen häufig nicht benötigt. Positive Werte für P und I deuten auf eine Gegenkopplung hin. Wenn jemand von Ihnen einen hochwertigen Holzpelletgrill besitzt, dann haben auch Sie wahrscheinlich einen PID-Regler.
Für die Zwecke dieses Artikels habe ich nur die P- oder Proportionalsteuerung implementiert und die Parameter I und D auf Null belassen. Genauer gesagt, habe ich implementiert:
Man beachte, dass das SARIMA-Modell, das von diesem Punkt an fortschreitet, auch alle vorherigen Schritte, die aus dem SARIMA-Modell abgeleitet wurden, sowie jegliche Rückkopplung enthält.
Nur mal so wollte ich sehen, wie viel negative Rückkopplung nötig wäre, um das Random-Walk-Modell von Abb. 5c an einen SP von Null zu binden. Es stellte sich heraus, dass ein Wert von nur etwa 1×10-³ Grad pro Monat für P ausreicht, um das zufällig wandernde Biest zu zähmen. Allerdings ist eine gewisse negative Rückkopplung erforderlich, um zu verhindern, dass die Abweichung von einem Anfangswert von Null mit der Zeit monoton zunimmt.
Das Modell in Abb. 5b ist viel stärker mit dem SP einer Temperaturanomalie von null Grad verankert, und deshalb sollten wir erwarten, dass es viel mehr Rückkopplung braucht, um diese Art von Zeitreihe vom Fall ohne PID-Regelung wegzubringen. Das liegt daran, dass in diesem Modell bereits eine Menge negativer Rückkopplung eingebaut ist. Ich zeige die Ergebnisse der Untersuchung der Auswirkungen zusätzlicher proportionaler Rückkopplung in Abb. 7, in der die maximale Abweichung von Null für eine Reihe von 1000-Jahre-Simulationen dargestellt ist. Die Abweichungen sind als Standardabweichungen (sigma) skaliert, wobei die Standardabweichung bei Null-Rückkopplung etwa 0,1748 Grad beträgt. Ist P positiv, liegt eine negative Rückkopplung vor, ist es negativ, liegt eine positive Rückkopplung vor. Für den Fall der Null-Rückkopplung kann man für die 12.000 Monate der Simulation eine maximale Abweichung von etwa 4 Sigma erwarten. Mit zunehmender negativer Rückkopplung sinkt die maximale Abweichung auf etwa 3 Sigma.
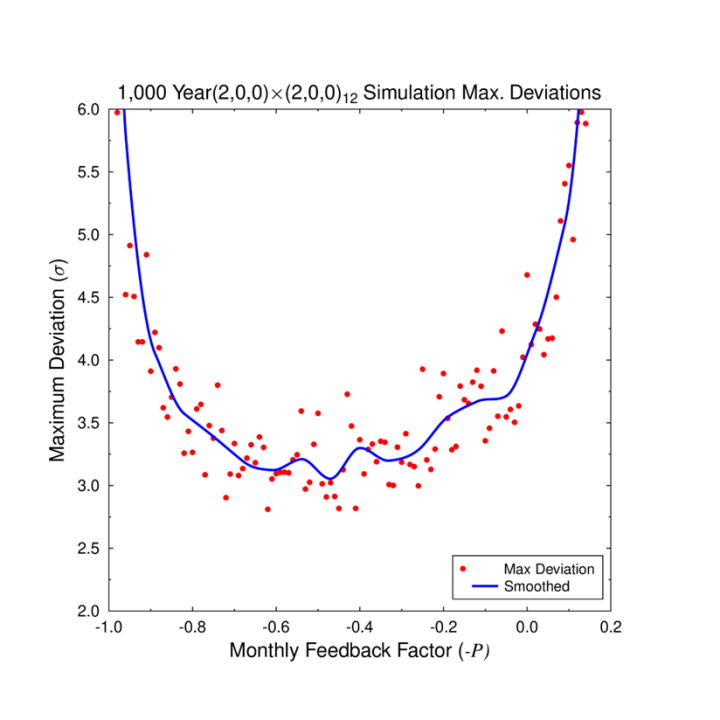
Abbildung 7: Maximale Abweichung für simulierte 12.000-Monats- (1.000-Jahres-) SARIMA-Simulationen auf der Grundlage der Anpassung (2,0,0)x(2,0,0)12 an die HadCRUT5-Temperaturaufzeichnung 1850-1950 plus einer Rückkopplungskorrektur auf der Grundlage eines konstanten Sollwerts.
Abb. 7 veranschaulicht jedoch auch etwas, das Ihnen Ihre Mutter wahrscheinlich beigebracht hat: Zu viel von allem kann schlecht sein. Bei extremer negativer Rückkopplung tritt ein Phänomen auf, das oft als „Hunting“ bezeichnet wird, d. h. die extreme Rückkopplung beginnt zu überkorrigieren, was zu immer stärkeren Schwingungen führt. Bei positiver Rückkopplung, bei der jede Störung des Systems vergrößert wird, setzt dieses Verhalten sogar noch früher ein. Tatsächlich explodiert das System bei einem -P-Wert von mehr als 0,19 vollständig.
Schlussfolgerung
Daraus schließe ich, dass es keine sehr starke positive Temperaturrückkopplung innerhalb des Klimasystems geben kann, wenn die „normale“ oder vorindustrielle Temperaturaufzeichnung völlig flach ist. Es ist möglich, dass es eine verzögerte Auswirkung des Wasserdampfanstiegs aufgrund eines Temperaturanstiegs gibt, aber dies könnte mit dem Parameter „I“ eines PID-Reglers berücksichtigt werden. Dieser Parameter kann ebenso leicht zu Instabilitäten führen wie der Parameter P. Wenn die Atmosphäre über den Ozeanen im Durchschnitt um ein paar Zehntel Grad steigt, warum sollte es dann mehr als einen Monat dauern, bis der Wasserdampfanteil in der Atmosphäre steigt? Im Grunde will ich damit sagen, dass, wenn ein Anstieg von 1°K aufgrund eines Anstiegs des CO₂ tatsächlich zu einem Temperaturanstieg von 2°K aufgrund einer positiven Rückkopplung führt, jede Störung der Temperatur aus irgendeinem Grund aufgrund einer positiven Rückkopplung ebenfalls verstärkt werden sollte.
Natürlich kann ein Teil oder vielleicht sogar der größte Teil des „Rauschens“ in unserer bestehenden Temperaturaufzeichnung auf Messungen oder instrumentelles Rauschen zurückzuführen sein. Wenn das der Fall ist, dann ändert sich in dieser Geschichte nur die Größe der Komponente des weißen Rauschens. Die allgemeine Temperaturrückkopplung muss in jedem Klimamodell berücksichtigt werden, wenn man gleichzeitig die Gleichgewichts-Klimasensitivität von Kohlendioxid über den Mechanismus der positiven Temperaturrückkopplung erhöhen will.
Reference
Kaufman, D., McKay, N., Routson, C., Erb, M., Davis, B., Heiri, O., Jaccard, S., Tierney, J., Dätwyler, C., Axford, Y. and Brussel, T., 2020. A global database of Holocene paleotemperature records. Scientific data, 7(1), p.115.
Link: https://wattsupwiththat.com/2024/02/13/temperature-feedback-follies/
Übersetzt von Christian Freuer für das EIKE