Der gemeine Küchenherd als Beispiel für die Anwendung des Stefan-Boltzmann-Gesetzes – Teil 1 - EIKE - Europäisches Institut für Klima & Energie

von Uli Weber

(A) Vorbemerkung: Ich hatte in der fernen Vergangenheit oft die populärwissenschaftlichen Aussagen von US-amerikanischen Wissenschaftlern bewundert, deren stark vereinfachende Erklärungen allgemeinverständlich waren, ohne grob fehlerhaft zu sein. Von einem aktuellen Fortbestand dieser hohen Kunst ist mir in den Zeiten spontaner Empörung und hochmoralischem Mobbing leider nichts bekannt. Denn dazu gehört nunmal auch auf Seiten von selbsternannten „Fachleuten“ und sogenannten „Faktencheckern“ eine Kultur des Zulassens solcher allgemeinverständlichen Beschreibungen ohne spontan-cholerische Besserwisseranfälle, die solche Bemühungen konterkarieren. Schon die Mathematik scheint in der gegenwärtigen Kommunikation an frühe Verständnisgrenzen zu stoßen, und die Physik bedient sich der Mathematik lediglich als Formalsprache. Im aktuellen EIKE-Artikel von Dr. Hans Hofmann-Reinecke heißt es dazu, Zitat mit Hervorhebungen:

„Unsere grassierende Inkompetenz in Sachen Mathematik ist kein rein akademisches Problem, sie hat dramatische Konsequenzen, auch für die deutsche Politik. Dabei geht es nicht etwa um Fehler bei den letzten Stellen hinterm Komma, es geht um das Verkennen von Größenordnungen. Diese kognitive Behinderung führt zu katastrophalen Entscheidungen durch unsere „Politiker-innen“. Da aber die Mehrheit der Bevölkerung auch nicht besser rechnen kann, ist sie nicht in der Lage, das Versagen der Verantwortlichen zu erkennen und sie dafür zur Rechenschaft zu ziehen.“

Das vorstehend Gesagte gilt umso mehr für komplizierte physikalische Vorgänge, wenn dem geneigten Leser in unserer MINT-fernen Gesellschaft zusätzlich auch noch grundlegende physikalische Begriffe unbekannt sind, selbst wenn er denn eigenständig rechnen könnte. Was nun mein hemisphärisches Stefan-Boltzmann-Modell betrifft, mit dem ich den sogenannten „natürlichen atmosphärischen Treibhauseffekt“ widerlegt hatte, so sind mir in der Vergangenheit drei Sorten von „Total-Quatsch“-Kritikern untergekommen. Die Hälfte dieser Kritiker besteht aus Professoren mit unterschiedlichen Schwerpunkten in Physik oder Chemie, die altersgemäß-intellektuell ihren ganz persönlich interpretierten „atmosphärischen Treibhauseffekt“ nicht mehr loslassen wollen oder können, ein weiteres Viertel davon sind Dunning-Krüger-Schmalspurphysiker, die nur ihre eigene vorgefasste Meinung (aner)kennen, und das letzte Viertel besteht aus sophistisch vorgebildeten Trollen der Klimakirche. Unter diesen Voraussetzungen ist es ziemlich ungünstig, sich mit stark vereinfachenden Beispielen zusätzlich angreifbar zu machen. Daher werde ich das jetzt mal versuchen und setze dabei einfach die Grundrechenarten ganz frech voraus.

(B) Fangen wir also mal mit den physikalischen Einheiten an: Physikalische Berechnungen bestehen nicht nur aus Zahlen und Symbolen, bestimmend sind vielmehr die jeweilig korrekten [physikalischen Einheiten]. Nehmen wir einmal an, Ihr Auto hätte eine Leistung von 100 [kW], das sind [k=kilo=1.000] mal 100 [Watt], also so viel wie 1.000 von den inzwischen verfemten 100 [Watt] Glühbirnen. Diese Leistung hat Ihr Auto immer, auch wenn es in der Garage steht. Und wenn Sie sich jetzt wundern, dass Ihr Auto dann gar nicht leuchtet, das tut die Glühbirne auch nicht, solange kein Strom fließt. Man nennt die Fähigkeit eines Körpers, Arbeit zu verrichten, physikalisch „Leistung“ (Einheit Watt [W]), und zwar auch dann, wenn dieser Körper momentan gar nichts leistet, sondern sich in der Garage oder im Supermarkt-Regal ausruht. Wenn Sie aber den Lichtschalter umlegen, dann läuft die Zeit, die Glühbirne verbraucht diese 100 [Watt] an elektrischem Strom und liefert Ihnen dafür Licht. Und wenn Sie diese Glühbirne jetzt 12 Stunden brennen lassen, dann stellt Ihnen Ihr Stromversorger dafür 12 Stunden mal 100 Watt in Rechnung, also 1,2 Kilowattstunden. Diese 1,2 Kilowattstunden bestehen also aus 100 Watt [W] mal 12 Stunden [h] gleich 1.200 Wattstunden [Wh] und nennen sich physikalisch „Arbeit“. Arbeit ist also Leistung [Watt] mal Zeit [Zeiteinheit], oder

Arbeit: 1 [Wh] = 1 [W] x 60 [min = 60sek] = 3.600 [Watt x Sekunden] [= Joule = Ws]

Zum Durchschnitt von physikalischer Arbeit: Nehmen wir jetzt einmal an, Sie haben für diese Glühbirne einen eigenen Stromzähler und lassen sie an 182,5 Tagen im Jahr brennen. Nach genau einem Jahr stellen Sie fest, dass Ihre Glühbirne 100 Watt x 182,5 Tage [=d] Strom verbraucht hat, also

100 [W] x 182,5[d] x 24[h] = 438.000 [Wh] x 3.600[s] = 1.576.800.000 [Ws oder Joule]

Nun sind Sie aber vielleicht schon etwas älter und ein bisschen vergesslich. Daher wissen Sie nicht mehr so genau, wie lange Sie die Glühbirne haben brennen lassen. Dummerweise ist auch die Leistungsangabe auf der Glühbirne nicht mehr lesbar, sodass Sie weder die tatsächliche Brenndauer noch die Leistung der Glühbirne aus dem Stromverbrauch physikalisch korrekt rückrechnen können, wie es sonst eigentlich möglich wäre:

Brenndauer der Glühbirne = 438.000 [Wh] / 100 [W] = 4.380 [Stunden =h]

Leistung der Glühbirne = 438.000 [Wh] / 4.380 [Stunden =h]= 100 [Watt]

Anmerkung: Wie Sie sicher bereits gemerkt haben, stehen physikalische Einheiten oft in eckigen Klammern. Diese physikalischen Einheiten müssen sich auf beiden Seiten des Gleichheitszeichens entsprechen und unterliegen ebenso den Regeln der Mathematik wie die davor stehenden Zahlen, also beispielsweise: 100 [Ws] / 10 [s] = 10 [W]

Ihnen bleibt jetzt also nur noch eine rein mathematische Rückrechnung, wobei Sie entweder die Leistung der Glühbirne oder deren Brenndauer als bekannt voraussetzen müssen, im einfachsten Fall also beispielsweise das gesamte Abrechnungsjahr, weil Ihre Stromrechnung darauf lautet:

Der Gesamtverbrauch war 438.000 [Wh] / [a] – und das Jahr [a] hat 8.760 Stunden [h]

Daraus folgt: Leistung der Glühbirne = 438.000 [Wh] / 8.760 Stunden [h] = 50 [Watt =W]

In dem Moment, wo Sie aus einer vorhandenen „Leistung“ [W] durch Einbeziehung der „Zeit“ [s] eine „Arbeit“ [Joule=Ws] abfordern, geht Ihnen der physikalisch eindeutige Bezug zwischen „Leistung“ und „Zeit“ verloren. Sie müssen also mindestens eine der beiden tatsächlichen Eingangsgrößen kennen, um den originären physikalischen Bezug wieder herzustellen. Das Ergebnis von „Arbeit“ [Ws] ist also mathematisch richtig, kann aber rückblickend den tatsächlichen physikalischen Sachstand nicht mehr eindeutig aus sich heraus abbilden. Denn Sie hatten ja gar keine 50 W Glühbirne übers ganze Jahr brennen lassen, sondern eine 100 W Glühbirne für ein halbes Jahr.

(C) Das geheimnisvolle Stefan-Boltzmann-Gesetz: Nachdem wir nun die nötigen physikalischen Einheiten geklärt haben, wenden wir uns einmal dem geheimnisvollen Stefan-Boltzmann-Gesetz zu. Dieses physikalische Gesetz verknüpft die Temperatur eines Körpers mit seiner Abstrahlungsleistung:

P / A = C x T x T x T x T = C x T^⁴ mit

P = Strahlungsleistung in [W]

A = Fläche des Körpers in Quadratmetern [m x m = m^²]

C = Konstante (S-B-Konstante) [W/(m^² x K^⁴)]

T = Temperatur des Körpers bezogen auf den absoluten Nullpunkt

[0 Kelvin = 0 K]

Anmerkung: 0 Kelvin entspricht einer Temperatur von -273,15°C

Wir können diese Gleichung vereinfachen, indem wir eine spezifische Strahlungsleistung „S“ (= P / A) in [W/m^²] einführen und erhalten dann:

S [W/m^²] = C [W/(m^² x K^⁴)] x T^⁴ [K^⁴] Stefan-Boltzmann-Gesetz

Jeder Körper mit einer Temperatur größer 0 Kelvin, also größer als -273,15°C, strahlt mit einer spezifischen Strahlungsleistung, die sich direkt aus dem Stefan-Boltzmann-Gesetz ergibt. Wie Sie unschwer erkennen, kommt die Zeit [t] im Stefan-Boltzmann-Gesetz gar nicht vor. Dieses physikalische Gesetz gilt nämlich ausschließlich „just in Time“, also, ein Körper strahlt dann und nur dann die durch das Stefan-Boltzmann-Gesetzes vorgegebene spezifische Leistung ab, wenn er in diesem Augenblick auch ganz genau die dort vorgegebene Temperatur hat.

Temperatur [Kelvin]

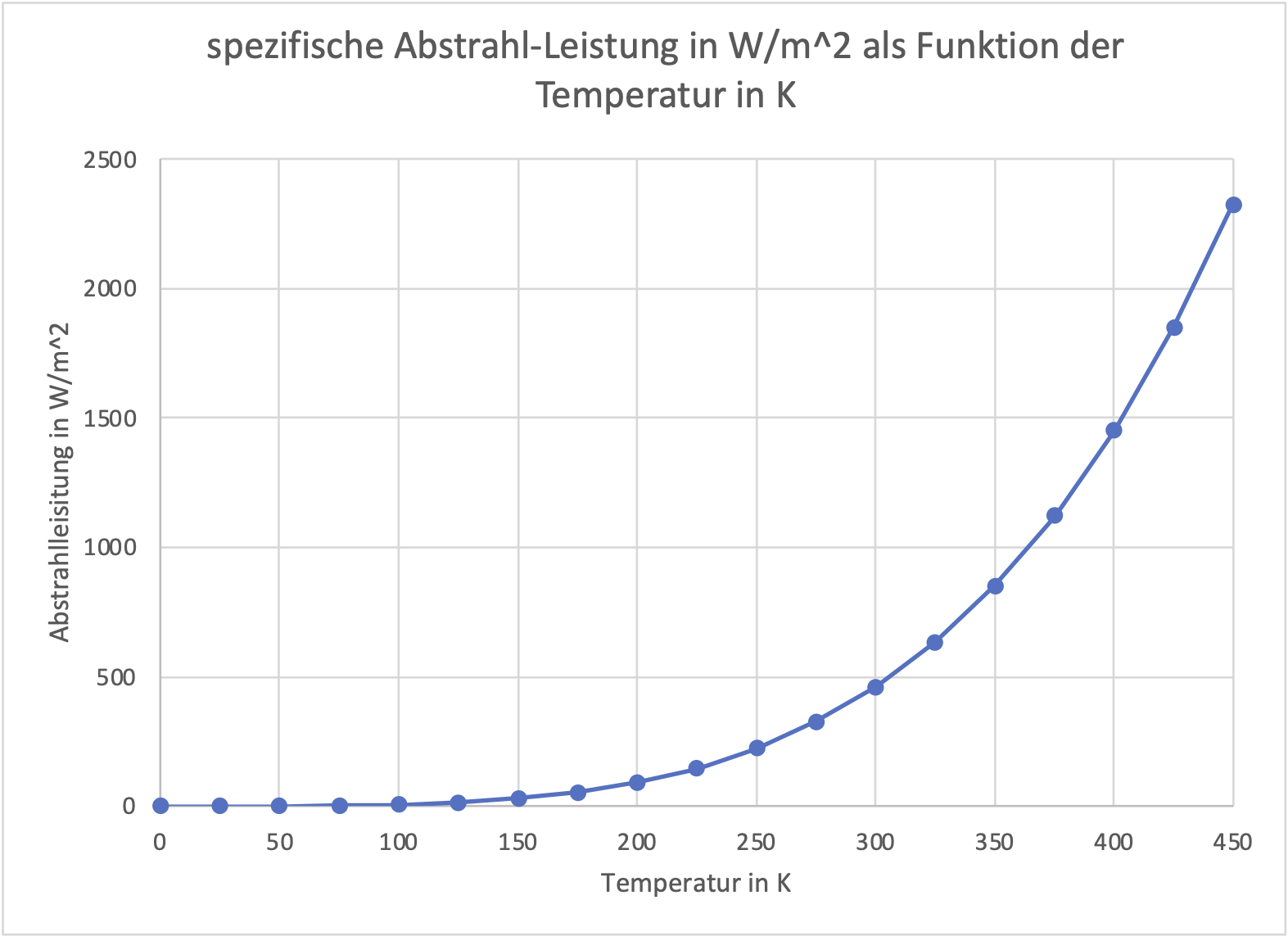
Abbildung: Die Abhängigkeit der spezifischen Strahlungsleistung [W/m^²] von der Temperatur [K] im Stefan-Boltzmann-Gesetz (mit freundlicher Genehmigung von M. Limburg)

Der in der vorstehenden Abbildung gezeigte Verlauf der Stefan-Boltzmann-Funktion ist durch eindeutige Wertepaare von Temperatur und spezifischer Strahlungsleistung gekennzeichnet. Eine mathematische Anwendung dieser Funktion auf Mittelwerte ist physikalisch nicht erlaubt. In einer räumlichen Umgebung, die gegenüber einem betrachteten Körper sehr groß und massereich ist, tendiert dieser Körper dazu, die Temperatur seiner Umgebung anzunehmen. Wenn Sie also ein Eis aus dem Kühlschrank nehmen und sich eine Tasse Kaffee aufbrühen, dann ist das Eis kälter als die Umgebung und der Kaffee heißer. Wenn Sie dann gestört werden und Eis und Kaffee vergessen, werden Sie später feststellen, dass beides die Temperatur der Küche angenommen hat; das ist sowohl schlecht für das ehemals kalte Eis wie auch für den ehemals heißen Kaffee, und für Sie bleibt auch nichts Gescheites mehr übrig. Im Ergebnis hatte also das Eis so lange Strahlung aufgenommen, bis es die Temperatur der Umgebung angenommen hat, und der Kaffee hatte so lange Strahlung abgegeben, bis er ebenfalls diese Temperatur angenommen hatte. Nehmen Sie zum Beispiel eine Tiefkühlpizza und schieben Sie diese in den Ofen. Solange der Ofen nicht angeschaltet ist, schmilzt diese Tiefkühlpizza lediglich still vor sich hin und nimmt schließlich die Umgebungstemperatur des kalten Ofens an. Sie müssen also den Ofen anschalten und die vorgegebene Temperatur einstellen, damit Sie Ihre Tiefkühlpizza aufbacken können. Physikalische Gleichzeitigkeit bedeutet also, dass der Ofen genau dann Wärme erzeugen muss, wenn die Pizza im Ofen aufgebacken werden soll.

Sie finden das selbstverständlich? Naja, Tag und Nacht sind auch selbstverständlich, das weiß schon jedes Kindergartenkind. Nur in der Klimawissenschaft ist das immer noch nicht bekannt.

(D) Das glauben Sie nicht? – Dann schaunmermal der Klimawissenschaft genau auf die Finger:

Die strenge physikalische Gleichzeitigkeit im Stefan-Boltzmann-Gesetz gilt nicht nur für Ihre Pizza und den heißen Ofen, sie ist ebenfalls eine zwingende Voraussetzung für eine Stefan-Boltzmann-Inversion*. Inversion heißt in diesem Fall, dass, in Umkehrung des Stefan-Boltzmann-Gesetzes, eine spezifische Strahlungsleistung auf einen Körper einwirkt und dort eine Temperatur erzeugt. Und diese Temperatur folgt dann wiederum dem Stefan-Boltzmann-Gesetz. Soweit die Theorie, in der Praxis ist das gar nicht so einfach, wenn man die Temperatur der sonnenbeschienenen Erde berechnen will, denn es gibt auf unserer Erde nun mal Tag und Nacht:

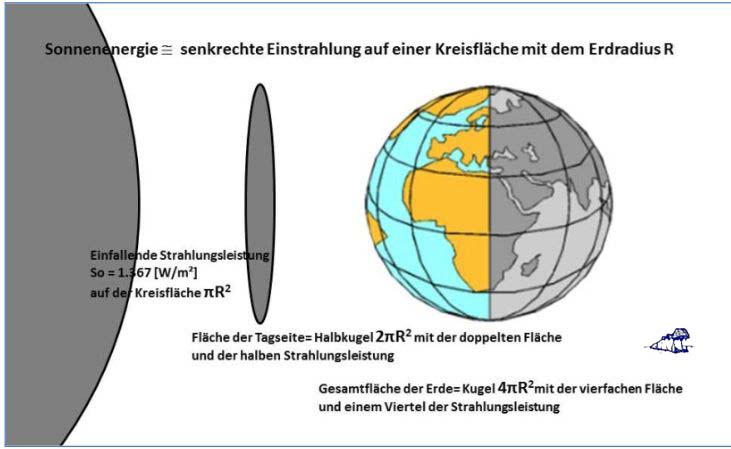
Abbildung: Die geometrischen Verhältnisse beim Einfall der Sonneneinstrahlung auf die Erde

Und das sind die bestimmenden Parameter:

Spezifische Strahlungsleistung der Sonne: 1.367 W/m² (= Solarkonstante)

Fläche des Lichtkegels, der auf die Erde fällt: Kreisfläche mit dem Erdradius R

Von der Sonne beschienene Fläche: Halbkugel mit dem Erdradius R

Gesamtoberfläche der Erde: Kugel mit dem Erdradius R

Kreisfläche, Halbkugelfläche und Kugelfläche verhalten sich zueinander wie 1 : 2 : 4

Und mit diesem Flächenverhältnis haben wir bereits den wesentlichen Knackpunkt für eine Stefan-Boltzmann-Inversion auf unserer Erde zu fassen. Beim S-B-Gesetz (Temperatur erzeugt Strahlung) hat der betreffende Körper nämlich eine einheitliche Temperatur und strahlt in alle Richtungen gleichmäßig ab. Bei der S-B-Inversion (Strahlung erzeugt Temperatur) ist das nicht so. Versuchen Sie einfach mal, einen Fußball komplett mit einer Taschenlampe zu beleuchten (danke für das schöne Beispiel, Herr W. Schulz), dann erkennen Sie das Problem sofort. Denn egal was Sie auch machen, die Rückseite des Fußballs bekommen Sie mit dem Lichtstrahl nie zu fassen. Nun könnte man mit der sogenannten „Klimawissenschaft“ argumentieren, dass sich die Erde unter dem Lichtkegel der Sonne ja einmal in 24 Stunden um sich selber dreht und einfach über diese 24 Stunden mitteln. Wir haben aber bereits gesehen, dass eine mathematische Mittelung über Dunkelzeiten physikalisch nicht so richtig funktioniert. Denn schließlich wäre die dunkle Nachtseite der Erde in einer solchen 24h-Mittelung ja immer mit enthalten. Nehmen wir jetzt also noch einmal unsere Tiefkühlpizza und stellen über einen gemeinsamen Stromzähler nebeneinander 2 Herde auf, die Tag- und Nachtseite der Erde repräsentieren sollen und jeweils 12 Stunden des 24h-Tages angeschaltet sind. Jeder dieser beiden Herde wird also für 12 Stunden mit 2 [kW] betrieben und danach kommt der andere Herd dran. Wenn Sie Ihre Pizza aufbacken wollen, dann müssen Sie daher je nach Tageszeit den jeweils eingeschalteten Herd auswählen. Über einen 24h-Tag liegt der Verbrauch beider Herde zusammen dann bei 48 [kWh]. Bezogen auf einen einzelnen Herd ergibt das jeweils einen Verbrauch von 24 [kWh] in 24 Stunden oder 1 [kW] pro Stunde. Wenn wir jetzt einmal vereinfachend eine lineare Beziehung zwischen Stromverbrauch und Temperatur unterstellen, dann würden echte 2 [kW] beispielsweise 200°C entsprechen, 1 [kW] Durchschnitt dagegen nur 100°C. Die 200°C reichen zum Aufbacken der Pizza in der vorgegebenen Zeit völlig aus; bei 100°C sehe das Ergebnis dagegen sehr viel langwieriger und trockener aus…

Wir sehen also, dass die Ableitung von Temperatur allein aus einer Energiemenge zu völlig unterschiedlichen Ergebnissen führen kann, je nachdem, ob die tatsächliche physikalische Situation in die Berechnung eingeht oder nicht. Man muss also in einer Stefan-Boltzmann-Inversion immer die tatsächliche „Just-in-Time“ Augenblicksleistung als physikalische Grundlage für die Berechnung der tatsächlichen Augenblickstemperatur verwenden.

Weiterhin gilt das Stefan-Boltzmann-Gesetz nur für einen sogenannten „schwarzen“ Körper. Das ist ein idealisierter Körper, der sämtliche Strahlung aufnimmt, die auf ihn trifft. Und hier kommt ein weiterer wichtiger Fachbegriff ins Spiel, und zwar die sogenannte „Weiße“ (Albedo) eines natürlichen Körpers. Diese „Weiße“ gibt an, wie viel der Einstrahlung ein solcher Körper zurückreflektiert. Während also ein „schwarzer“ Körper eine Albedo von „0“ hat, reflektiert eine Diskokugel die gesamte Strahlung und hat eine Albedo von „1“. Und die natürlichen Körper liegen als sogenannte „graue Körper“ irgendwo dazwischen, beispielsweise auch unsere Erde:

Abbildung: Earthrise, Farbbild, von Bill Anders – gemeinfrei (Wikipedia)

Alles, was Sie hier in dieser Abbildung von der Erde sehen ist das reflektierte Sonnenlicht, und das sind etwa 30% (oder 0,30 vom Ganzen=1) der Sonneneinstrahlung. Diese 30 Prozent müssen wir also schon einmal von der Solarkonstanten (1.367 W/m²) abziehen, wenn wir das Stefan-Boltzmann-Gesetz auf die Erde anwenden wollen. Es bleiben somit etwa 940 W/m² für die Erzeugung der Temperatur auf unserer Erde übrig. Wir können auf der obigen Abbildung die Tagseite und die Nachtseite unserer Erde deutlich unterscheiden. Weiterhin ändern sich über die Breitenkreise der Zenitwinkel der Sonne, also wie hoch die Sonne am Himmel steht. Deshalb fahren Sie im Urlaub beispielsweise gerne in den Süden, weil es dort bei höherem Sonnenstand wärmer ist als hier bei uns. Und über das Jahr ändert sich dann auch noch das Verhältnis zwischen Tageslicht und Nacht, was man bei uns Sommer und Winter nennt.

(E) Der sogenannte „natürliche atmosphärische Treibhauseffekt“: Die Klimawissenschaft macht sich die Berechnung der „theoretischen“ Temperatur unserer Erde nun denkbar einfach. Sie nimmt nämlich einfach die einfallende Sonnenstrahlung auf der Kreisfläche mit dem Erdradius, zieht den reflektierten Anteil von 30% (Albedo) davon ab und teilt diesen Betrag dann durch 4, weil die Kugelfläche der Erde viermal größer ist als die Kreisfläche der einfallenden Sonnenstrahlung. Im Ergebnis ergibt sich somit ein Wert von:

(Solarkonstante – 30% = 940 W/m²) / 4 = 235 W/m² für jeden Quadratmeter unserer Erde.

Mit dieser spezifischen Strahlungsleistung geht man nun in das Stefan-Boltzmann-Gesetz hinein und erhält -18°C für die „theoretische Temperatur“ unserer Erde. Die „tatsächlich gemessene globale Durchschnittstemperatur“ beträgt dagegen etwa +15°C**. Die Differenz von 33°C zwischen diesen beiden Temperaturen schreibt man nun einem „natürlichen atmosphärischen Treibhauseffekt“ zu, der durch sogenannte IR-aktive „Klimagase“, das sind mit absteigender Wichtigkeit Wasserdampf, CO₂, Methan und andere IR-aktive Gase, erzeugt werden soll. Wenn Sie nun einmal das Internet durchsuchen, dann werden Sie feststellen, dass der Wasserdampf nur noch sehr selten unter den „Klimagasen“ auftaucht. Das war vor etwa einem Jahrzehnt noch ganz anders; damals hatte der Wasserdampf bei weitem den größten Anteil am sogenannten „natürlichen atmosphärischen Treibhauseffekt“: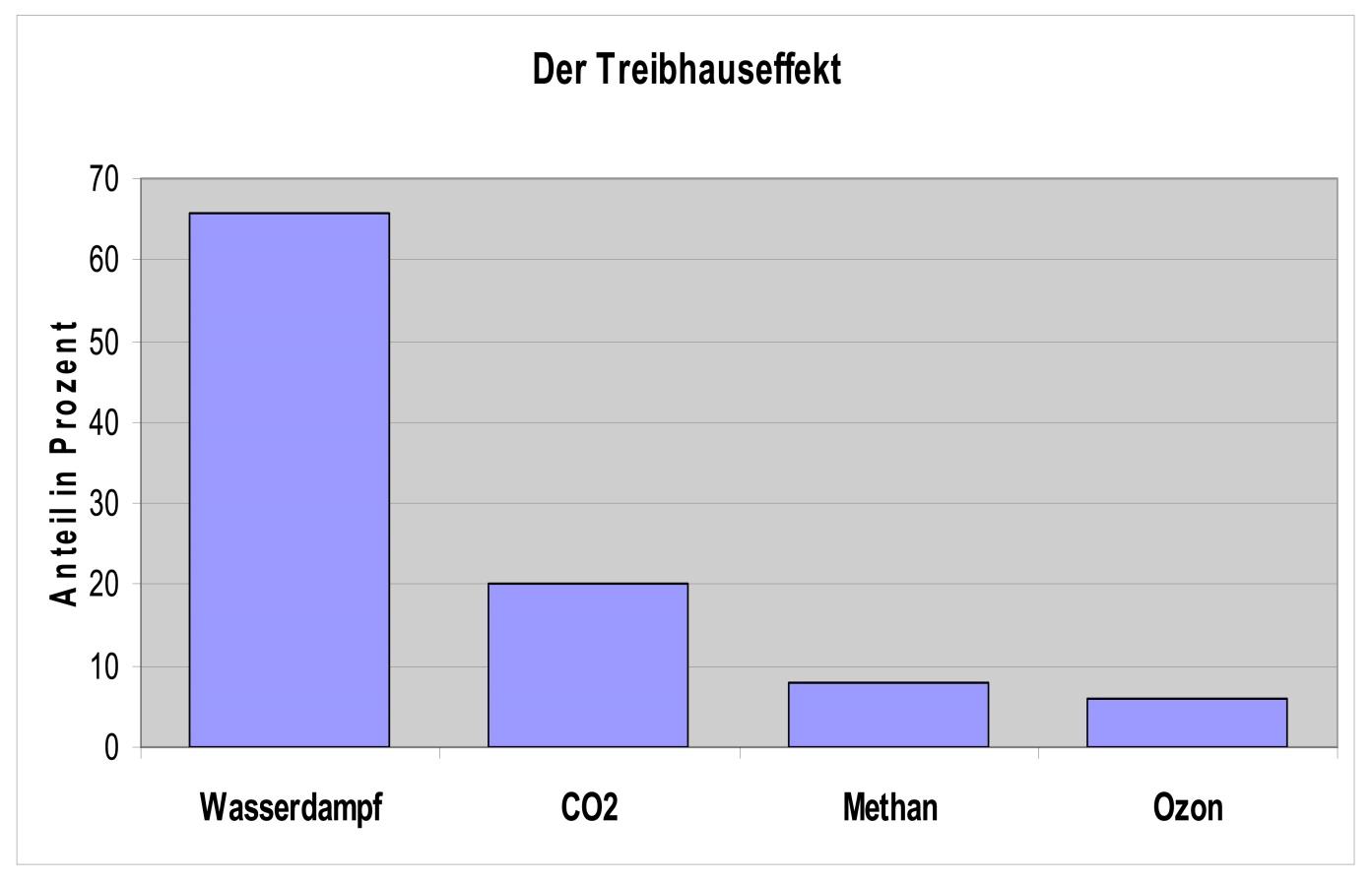 $C:\Users\Uli\Documents\Ablage & Archiv\Texte\Klimahysterie\Text 12 x 19\Charts\Charts skaliert\Chart 7.jpg$

Abbildung: Die gemittelten Anteile am sogenannten „natürlichen atmosphärischen Treibhauseffekt“

Quelle: Klimahysterie gefährdet die Freiheit Seite 57 (damals hat der Autor den THE noch „geglaubt“)

Das Problem von Klimawissenschaft und globaler Transformationspolitik war sicherlich der geringe Anteil von CO₂ am sogenannten „Treibhauseffekt“, denn der „menschengemachte“ CO₂-Anteil ist wiederum nur ein Bruchteil des natürlichen atmosphärischen CO₂. Die Argumentation für den Wegfall des Wasserdampfs ist daher ganz einfach. Mit der Temperatur steigt der Anteil von Wasserdampf in der Atmosphäre. Also werden die übrigen „Klimagase“ zu „primären Temperaturanheizern“ befördert, während Wasserdampf mit einem Beitrag von etwa 65% am sogenannten „Treibhauseffekt“ nur ein „Mitläufer“ ist, der lediglich auf einen solchen Temperaturanstieg reagiert – und damit ist er ‘raus aus der Betrachtung. Vielmehr wird sein Einfluss auf die „globale Durchschnittstemperatur“ den „primären Klimagasen“ einfach proportional, also je nach deren eigenem Anteil an diesem Temperaturanstieg, zugerechnet. Mit diesem Zaubertrick hat man dann auch gleich noch die natürlichen Klimaschwankungen von ca. 50% (IPCC) für den „menschengemachten Treibhauseffekt“ vereinnahmt. Was die platten Zahlen angeht, so ist der aktuelle Stand bei den atmosphärischen Anteilen von CO₂ und Wasserdampf:

Atmosphärisches CO₂: um 420 ppm – Wasserdampf im Mittel 0,4 %

Ich hoffe, diese Zahlen haben einen allgemeinen Aufschrei unter meinen Lesern bewirkt, denn die Äpfel und Birnen stimmen in diesem Vergleich nicht überein. Wenn schon ppm, dann muss man in einem direkten Vergleich beide Anteile in ppm angeben, und bei Prozent ist das ebenso, also:

Atmosphärisches CO₂: 420 ppm oder 0,042% – Wasserdampf 4.000 ppm oder 0,4 %

Mit der oben zitierten Argumentation kann man sich nun voll auf das lebensspendende CO₂ als „klimatisches Giftgas“ stürzen, wie die nachfolgende Abbildung vom Umweltbundesamt beweist:

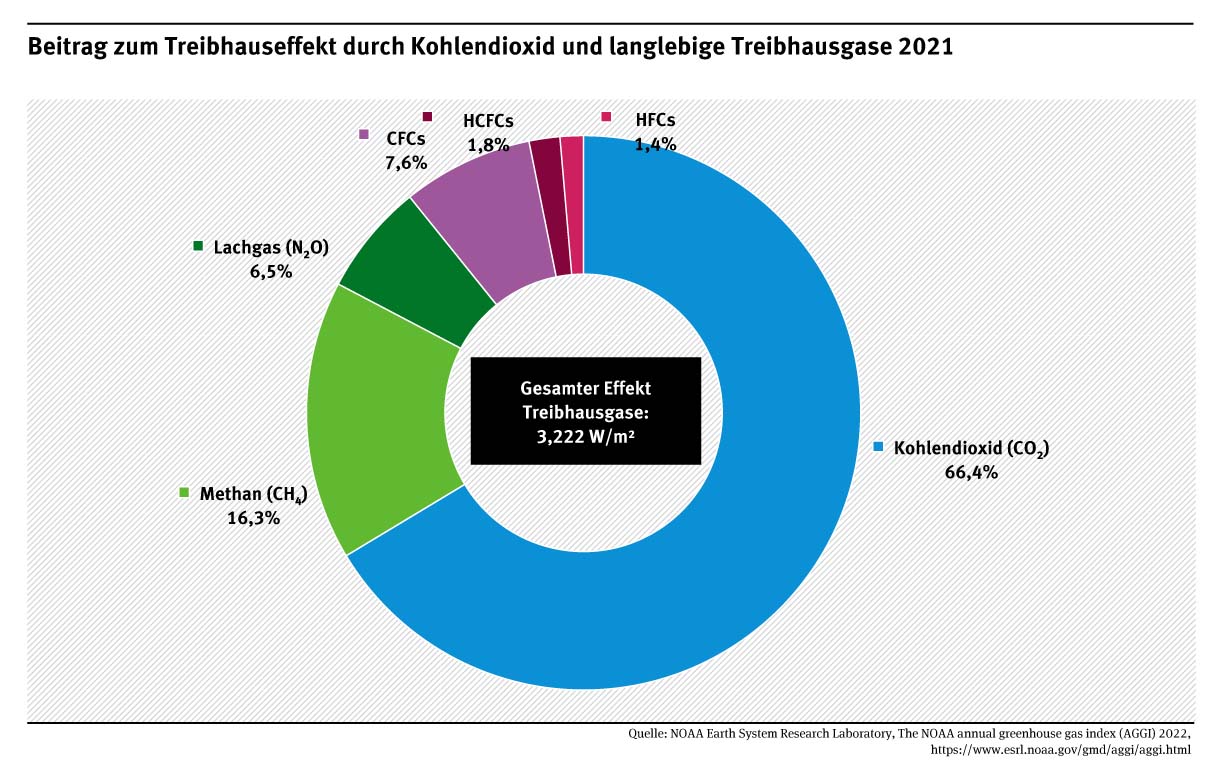Abbildung: Beitrag zum Treibhauseffekt durch Kohlendioxid und langlebige Treibhausgase 2021
Quelle: UBA mit Angabe: National Centers for Environmental Information (NOAA)

Im dazu gehörigen Text ist nirgendwo beschrieben, dass es sich bei dieser Kreisgrafik um lediglich etwa 30% des sogenannten „natürlichen atmosphärischen Treibhauseffektes“ handelt beziehungsweise der „Klimaeffekt“ von Wasserdampf bei den dargestellten „Klimagasen“ bereits mit eingerechnet ist. Das große Problem der sogenannten Klimakatastrophe soll nun vielmehr der stetig wachsende menschengemachte Anteil am atmosphärischen CO₂ durch die Verbrennung fossiler Energieträger sein, durch den dieser „Treibhauseffekt“ sich immer weiter verstärken und schließlich zu einer „Selbstverbrennung“ unserer Erde führen soll:

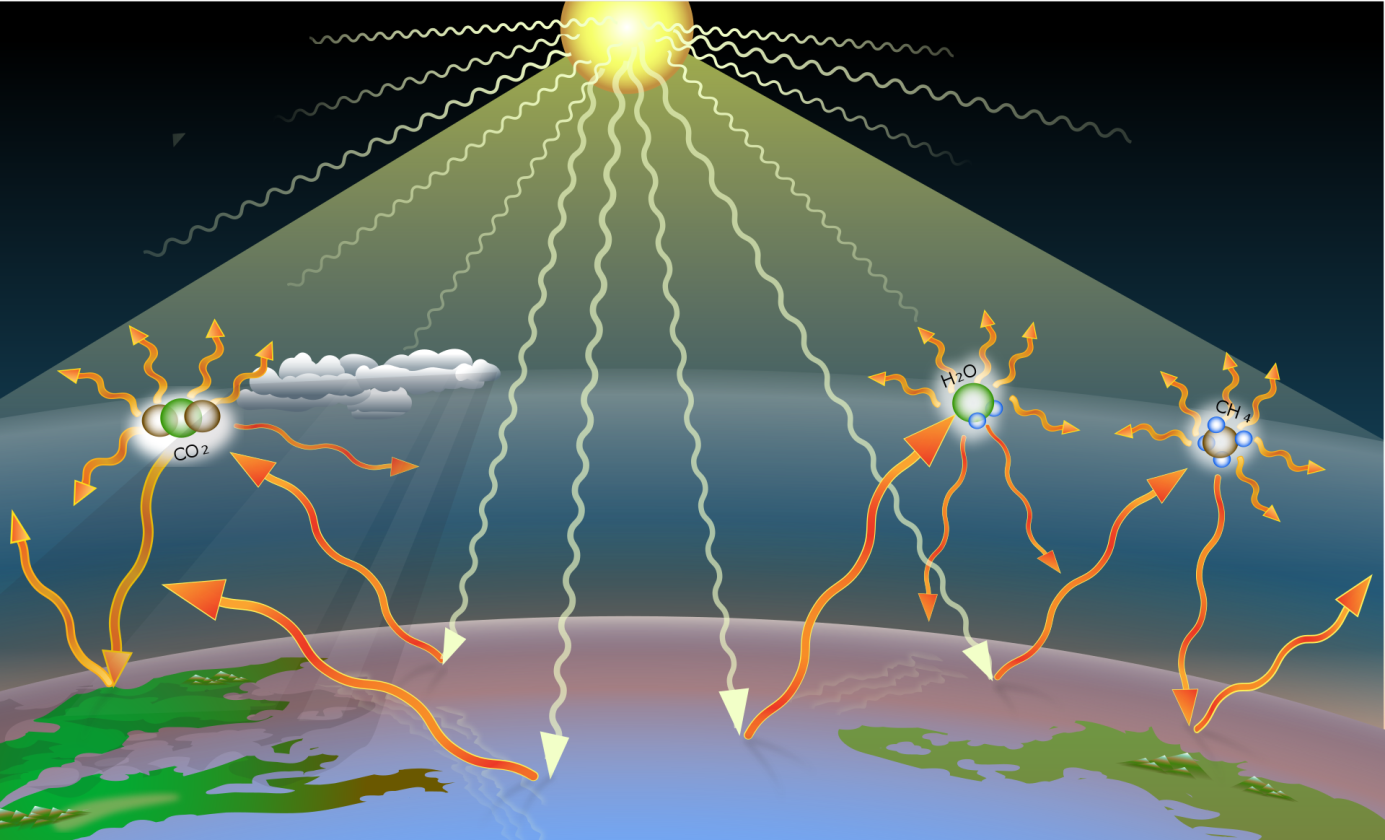
Abbildung: Der atmosphärische Treibhauseffekt (Wikipedia, Autor „A loose necktie“, Lizenz Creative Commons Attribution-Share Alike 4.0 International

Die Erklärung dazu lautet, Zitat: „Sonnenlicht (weiße Pfeile) wird auf der Erdoberfläche in Wärmestrahlung umgewandelt. Diese wird zurückgestrahlt (orange Pfeile). Ein Teil davon wird von Molekülen der Treibhausgase aufgenommen (Wasserdampf, Kohlendioxid und Methan) und in eine zufällige Richtung wieder emittiert, teilweise auch zurück zur Erde“.

Nix Genaueres über diesen sogenannten „natürlichen atmosphärischen Treibhauseffekt“ finden Sie übrigens auch beim Umwelt Bundesamt, das sich hinter historischen Fehlinterpretationen und schwammigen Vermutungen versteckt, ohne konkrete zahlenbasierte physikalische Mechanismen darzustellen. Wer’s etwas theoretischer mag, möge hier nachschauen…

Die Fortsetzung dieses Artikels erfolgt im 2. Teil: In Teil 2 wird zunächst das Kapitel (E) beendet, indem die Kenntnisse aus den Kapiteln (B) bis (D) auf die Berechnung der Klimawissenschaft für ihren „natürlichen atmosphärischen Treibhauseffekt“ angewendet und daraus Fragen abgeleitet werden. In Kapitel (F) erfolgt dann ein Abgleich dieser Fragestellungen mit den Gesetzen der physikalischen Wärmelehre. Als Gegenentwurf wird in Kapitel (G) dann mein hemisphärisches Stefan-Boltzmann-Modell vorgestellt. Und am Ende folgen in Kapitel (H) noch ein paar Nachweise, warum die mit meinem S-B-Modell berechnete und die gemessene Temperatur nicht übereinstimmen können.

Erklärungen

*) Stefan-Boltzmann-Inversion: Sowohl die klimawissenschaftliche Ableitung des Treibhauseffektes (THE) als auch mein hemisphärisches Stefan-Boltzmann-Modell stellen Inversionen des Stefan-Boltzmann-Gesetzes dar. In beiden Fällen wird aus der spezifischen Strahlungsleistung der Sonne eine Temperatur berechnet. Anstelle von (Temperatur erzeugt Strahlung) wird bei der Inversion also das S-B-Gesetz umgekehrt (Strahlung erzeugt Temperatur). Die Erwärmung eines Körpers durch Sonnenstrahlung kann jeder selber beobachten und überprüfen. Für eine genaue Berechnung müssen zusätzlich alle Randbedingungen des S-B-Gesetzes eingehalten werden, beispielsweise die zwingende Gleichzeitigkeit von Temperatur und Strahlung sowie die exakten geometrischen Verhältnisse bei der Einstrahlung. Das ist bei der klimawissenschaftlichen Faktor4-Berechnung des THE aber nicht der Fall.

**) Die „tatsächlich gemessene globale Durchschnittstemperatur“ von etwa +15°C: Diese „gemessene globale Durchschnittstemperatur“ ist eine Schimäre, denn dafür gibt es kein exaktes und nachvollziehbares „Kochrezept“ und keine zuverlässige Datengrundlage. Der interessierte Leser findet dazu die detaillierten Analysen und Ausführungen von Herrn Dipl.-Ing. Limburg hier und hier auf EIKE. Die Differenz dieser aktuell „gemessenen“ Globaltemperatur zu einer „vorindustriellen Temperatur“ stellt nun aber die Grundlage für die Sage von der „menschengemachten Klimakatastrophe“ dar. Der Menschen soll nämlich durch die Nutzung von fossilen Energieträgern und dem damit verbundenen Ausstoß von CO₂ einen Temperaturanstieg verursachen, der schließlich das Ende der Menschheit herbeiführen soll. Aber selbstverständlich gibt es für die ominöse „vorindustrielle Globaltemperatur“ auch kein Kochrezept und keine nachvollziehbare Datengrundlage. Inzwischen werden sogar fast nur noch Differenzen zwischen dieser „vorindustriellen Temperatur und der angeblich „gemessenen globalen Durchschnittstemperatur“ veröffentlicht. Das wiederum ist ganz natürlich, denn es gab und gibt gar keine globalen vorindustriellen Daten, wie die nachstehende Abbildung beweist:

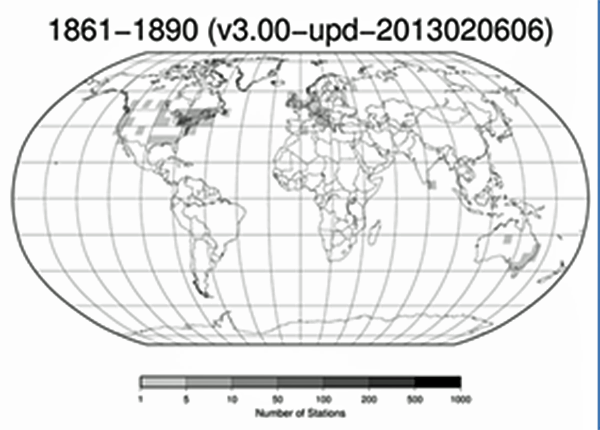Abbildung: NOAA Global Historical Climatology Network: Gebiete mit mehr als 10 Jahren kontinuierlicher Temperaturaufzeichnung im Zeitraum 1861-1890 (rechts, grau unterlegt)

Anmerkung: Der angegebene Link aus 2020 funktioniert aktuell nicht mehr.

Die Industrialisierung begann in der 1. Hälfte des 19. Jahrhunderts. Es gibt aber selbst aus der 2. Hälfte des 19. Jahrhunderts keine weltumspannenden Temperaturdaten, lediglich aus Teilen der USA, Europa, Ceylon und Australien liegen solche Daten vor. Das reicht für eine Globaltemperatur schon mal nicht aus. Vielleicht wird jetzt auch klar, warum die „gemessene globale Durchschnittstemperatur“ nur noch als Differenz zu einem ungenannten Fixwert angegeben wird – und gleichzeitig das oben abgebildete Beweismittel verschwunden ist…