Von Henri Masson, Professor (emeritus) an der University of Antwerp (Belgium) und Michael Limburg Dipl. Ing.

Dieser Artikel wiederholt weitgehend einen Teil des Vortrags, den der Autor Henri Masson auf der 12. jährlichen EIKE-Konferenz (München 2018) gehalten hat. Der Text, der die PowerPoint-Folien der Präsentation umgibt, ist jedoch unveröffentlicht, ebenso wie das, was den Kern dieser Studie ausmacht: die Analyse der Anpassungs-Residuen von Hadcrut 5.0.1.0-Daten durch eine Summe von Sinuskurven oder eine lineare Regressionslinie.

Der Beitrag wurde aus praktischen Gründen in 4 Teile aufgeteilt

Das Video dazu findet man hier. 

Teil 2

Zeitliche Mittelwerte

Der IPCC drückt seine Ergebnisse in Form von Monats- oder Jahres-Durchschnittswerten aus.

Es kommt vor, dass nicht nur die Sonne, sondern auch der Mond, der zwar kleiner ist, aber viel näher an der Erde steht, die lokale Sonneneinstrahlung verändert, wobei die Gravitationskräfte (das berühmte Problem der drei Körper in der Mechanik) die Ausrichtung der Rotationsachse der Erde und damit ihre Neigung gegenüber der Ebene der Ekliptik leicht verändern (Abbildung 7). Nun gibt es in einem Sonnenjahr mathematisch gesehen 13 Mondmonate (365/28 ~ 13,04), während der Kalender, mit dem wir die monatlichen Durchschnittswerte berechnen, 12 Monate von ungleicher Länge enthält. Daraus folgt, dass ein Datum des Sonnenkalenders von Jahr zu Jahr mit verschiedenen Mondphasen übereinstimmt. Diese Tatsache, die den Gärtnern, die „mit dem Mond pflanzen“, wohl bekannt ist, wird von den Klimatologen völlig vernachlässigt. Zum Leidwesen der Letzteren ergibt sich daraus auch von Sonnenjahr zu Sonnenjahr ein Rest an zeitlicher Anpassung der Amplitude, vergleichbar mit den Temperaturanomalien, die als Indikator für den Klimawandel gelten. Dies macht das Ganze sehr unübersichtlich.

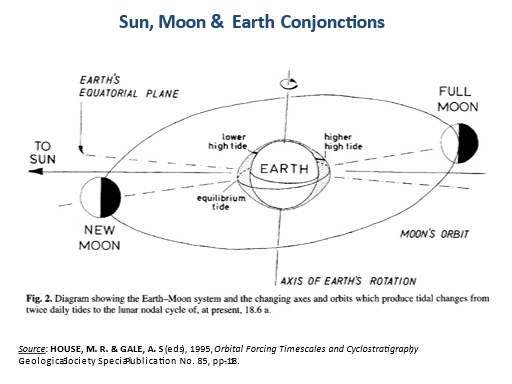
Abbildung 7: System Erde-Sonne-Mond.

Diese Tatsache wird vernachlässigt, da die Temperaturschwankungen von einem Tag auf den anderen nur sehr selten berücksichtigt werden und die größte zeitliche Auflösung bei einem Monat liegt. Betrachtet man jedoch die täglichen Temperaturschwankungen an einem bestimmten Punkt, so ist eine Periodizität von ~14 Tagen (ungefähr die Harmonische der Größenordnung von 2 bis 29,3 Tagen, die den Mondmonat kennzeichnet) deutlich erkennbar, wie in Abbildung 8 unten dargestellt:

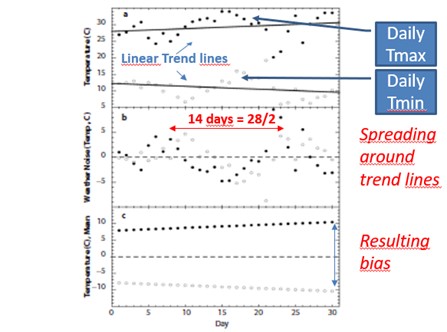
Abbildung 8: Tägliche Temperaturmessung. Eine Periodizität von 14 Tagen ist in der Aufzeichnung von Höchst-, Tiefst- und Durchschnittstemperaturen, zusätzlich zu einer langsamen Drift entsprechend den jährlichen Schwankungen offensichtlich. Die Amplitude dieser Periodizität von 14 Tagen ist in der Größenordnung von ±5°C um den Durchschnitt in dem gewählten Beispiel (Vanwvskvlei, Südafrika). Die Häufigkeitsanalyse der täglichen Daten, die an verschiedenen Orten für verschiedene Monate des Jahres gesammelt wurden, zeigt die gleichen Merkmale mit unterschiedlichen Amplituden und natürlich mit einem monatlichen Trend, der sich je nach Jahreszeit ändert. (Quelle: P. Frank, Imposed and Neglected Uncertainty in the Global Average Surface Air Temperature Index, Energy & Environment – Vol. 22, No. 4, 2011)

Die durch diese kalendarische Diskrepanz verursachten Fehler lassen sich einfach dadurch veranschaulichen, dass man einem Dutzend Sinuskurven von 365,25 Tagen eine Sinuskurve mit geringerer Amplitude und einer Periode von 29,53 Tagen überlagert. Um das Signal zu verrauschen, wurden einige Sinuskurven mit sehr geringer Amplitude hinzugefügt. Ihre Perioden entsprechen den bekannten astrophysikalischen Zyklen, die die Umlaufbahnen der Erde um die Sonne und des Mondes um die Erde stören. Die verwendeten Parameter sind in der folgenden Tabelle 1 zusammengefasst:

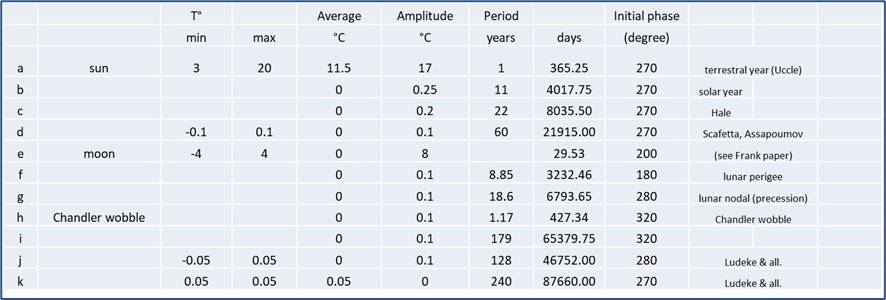
Tabelle 1. Parameter, die zur Simulation der Wechselwirkungen zwischen Sonnen- und Mondkalender verwendet werden. Zusätzlich zum Sonnenjahr und zum Mondmonat wurden verschiedene gut dokumentierte Periodizitäten von Mond und Sonne mit einer kleinen Amplitude hinzugefügt, um das natürliche Rauschen zu simulieren.

Einige illustrative Ergebnisse der Simulation sind in den Abbildungen 9, 10 und 11 wiedergegeben:

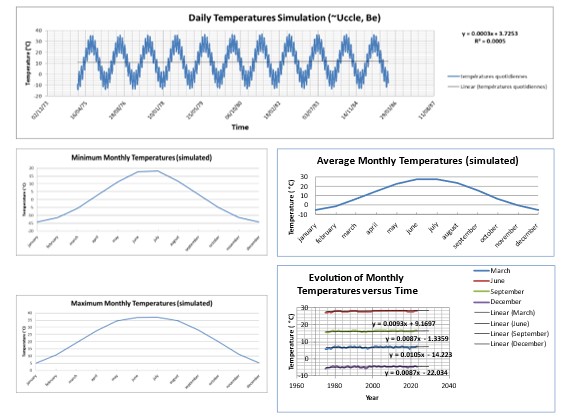
Abbildung 9: Simulation der monatlichen Durchschnittswerte (Sonnenkalender), die sich aus der Überlagerung einer Sinuskurve mit einer Periode von 365 Tagen und einer anderen mit einer Periode von 28 Tagen ergeben.

Die Entwicklung der simulierten monatlichen Temperaturen ist in Abbildung 10 dargestellt. Für den gewählten Wert der Parameter ergibt sich ein mit den Temperaturanomalien vergleichbares Profil mit einer positiven Steigung der Regressionslinie. Der IPCC führt die Ausschläge der Kurve auf kurzlebige natürliche Phänomene zurück (El Nino, Vulkanismus usw.). Es sei darauf hingewiesen, dass die Simulation auch eine „Pause“ aufweist, wie die aus Wetterdaten berechneten Temperaturanomalien.

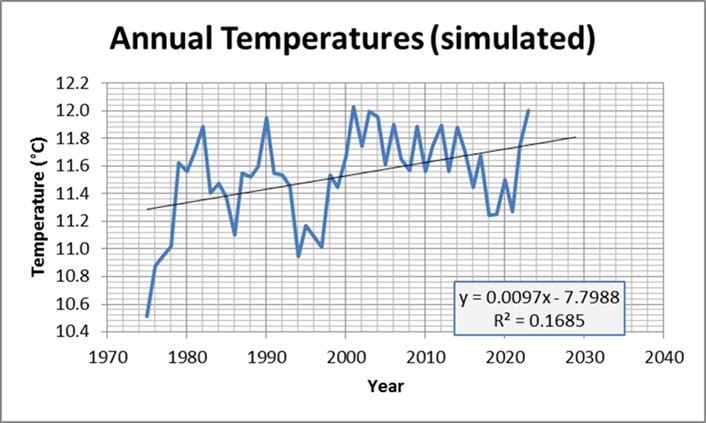
Abbildung 10: Simulation der Temperaturanomalien, die sich aus der Überlagerung einer Sinuskurve mit einer Periode von 365 Tagen und einer weiteren mit einer Periode von 28 Tagen ergeben. Das Ausmaß und die Amplitude sind mit den vom IPCC gemeldeten Temperaturanomalien vergleichbar. Die Regressionslinie hat eine positive Steigung, während das Signal vollkommen stationär ist. Die Ausschläge der Kurve wurden „künstlich“ mit fiktiven Ereignissen in Verbindung gebracht, um die Erklärungen des IPCC angesichts eines solchen Ergebnisses wiederzugeben.

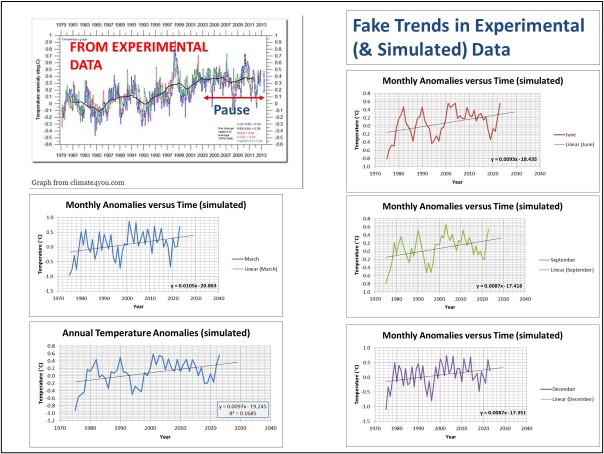
Abbildung 11: Vergleich zwischen realen und simulierten Anomalien (erhalten durch Überlagerung einer Sinuskurve mit einer Periode von 365 Tagen und einer anderen mit einer Periode von 28 Tagen). Die experimentelle Kurve befindet sich in der oberen linken Ecke der Abbildung. Alle anderen Abbildungen sind Simulationen jährlicher oder monatlicher Zeitreihen; ihre Regressionslinien zeigen einen positiven Trend.

Abbildung 11 ermöglicht einen direkten Vergleich dieser Simulationen mit den Temperaturanomalien. Die Ähnlichkeit ist frappierend. Wir überlassen es dem Leser, seine eigenen Schlussfolgerungen zu ziehen.

Am Rande sei bemerkt, dass die Amplitude der Gezeiten des Ozeans im Wesentlichen auf die Wirkung des Mondes zurückzuführen ist, die durch die Wirkung der Position der Sonne moduliert wird, die hohe Gezeiten verursacht und die Verteilung der Meeresströmungen beeinflusst. Es ist nicht ausgeschlossen, dass die gleichen Gravitationskräfte die Struktur und die Dynamik der Atmosphäre beeinflussen, die eine 1000-mal geringere Trägheit als der Ozean aufweist, z. B. auf die Position der Jetstreams oder die Merkmale der Walker-Zirkulation, der Hadley-Zellen oder der Polarzellen, auch wenn es keine genauen Daten gibt.

Diese variable Phasenverschiebung von Jahr zu Jahr zwischen Sonnen- und Mondkalender ist auch der Grund dafür, dass der Ramadan, der auf einem Mondkalender basiert, von Jahr zu Jahr zu unterschiedlichen Zeiten stattfindet, die sich auf den Sonnenkalender beziehen.

Lokale Temperatur-Anomalien

Aber selbst wenn wir uns auf die Verwendung lokaler Indikatoren beschränken, bleiben Probleme bestehen. Das von der WMO (World Meteological Association) befürwortete Konzept der lokalen Temperaturanomalie besteht darin, die an einem Punkt beobachtete Temperatur mit dem über einen bestimmten Bezugszeitraum von 30 Jahren errechneten Durchschnitt zu vergleichen. Die Rechtfertigung für Temperaturanomalien liegt in der Tatsache, dass es sich um eine bequeme Methode für den Vergleich von Temperaturschwankungen an verschiedenen Punkten der Erde handelt, wobei die lokalen Temperaturen zwischen den Polen und dem Äquator um bis zu 100°C variieren. Ursprünglich war vereinbart worden, den Bezugszeitraum alle 30 Jahre neu zu bestimmen (1930-1960, 1960-1990, 1990-2020). Die letzte Anpassung ist immer noch Gegenstand heftiger Debatten, wobei die WMO es vorzieht, den Referenzzeitraum 1960-1990 beizubehalten. Einige, die von der „offiziellen Klimawissenschaft“ als Verschwörungstheoretiker bezeichnet werden, sehen darin den verzweifelten Versuch, die Tatsache zu verschleiern, dass diese Anomalien im Vergleich zum Zeitraum 1990-2020 eine bedauerliche Tendenz zur Stagnation aufweisen, was die politische Agenda im Zusammenhang mit dem (so genannten) Klimanotstand ernsthaft beeinträchtigt.

Leider führen die Temperaturanomalien zu falschen Trends und Verzerrungen, die durch natürliche zyklische Temperaturkomponenten verursacht werden, deren Zeitraum den für die Berechnung der Anomalien verwendeten Referenzzeitraum (30 Jahre) überschreitet, und solche natürlichen Klimakomponenten sind zahlreich (siehe Tabelle 2).

Tabelle 2: Einige natürliche Zyklen im Vergleich zu dem für die Berechnung der Temperaturanomalien verwendeten Bezugszeitraum.

Veranschaulichen wir den Mechanismus anhand einer einfachen Sinuskurve mit einer Periode von 180 Jahren (eine bekannte periodische Komponente der Klimazeitreihen) und sehen wir uns an, was die Berechnung der Anomalien entlang dieser Sinuskurve ergeben würde, wobei der Bezugszeitraum wie üblich 30 Jahre beträgt (Abbildung 12):

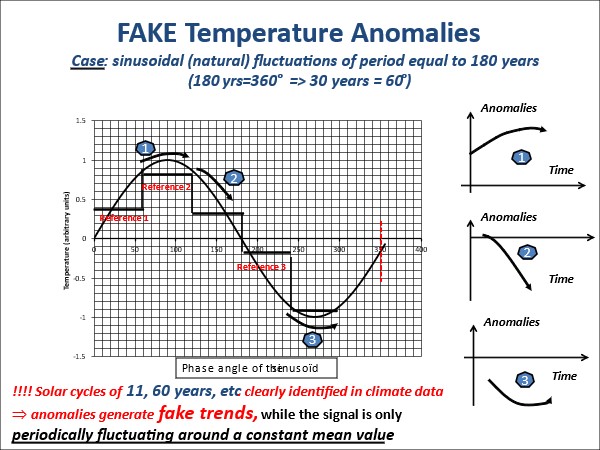
Abbildung 12: Simulation des Ausmaßes der Temperaturanomalien. Die Berechnung erfolgt für eine Sinusperiode von 360° und für Referenzperioden, die zur Berechnung der Anomalien verwendet werden, von 60° (dies entspricht einer Periode von 180 Jahren und einer Referenzperiode zur Berechnung der Anomalien von 30 Jahren). Diese Bezugszeiträume sind durch die roten Linien in der Abbildung dargestellt. Eine Sinuskurve zeigt natürlich keine Tendenz und entwickelt sich um eine Horizontale. Die drei dargestellten Fälle zeigen signifikante Anomalien, die sich deutlich voneinander unterscheiden und alle fiktiv sind.

Zusätzlich zu den falschen Tendenzen führt das Konzept der Anomalie im Falle eines polyzyklischen Signals auch zu variablen Verzerrungen in Abhängigkeit von der Anfangszeit und der Länge des Referenzzeitraums. Dieser Effekt wurde in Abbildung 13 für den Fall einer einfachen Sinuskurve simuliert. Dieser Effekt führt nicht nur zu Verzerrungen, sondern auch zu Diskontinuitäten beim Übergang von einer Referenzperiode zur anderen.

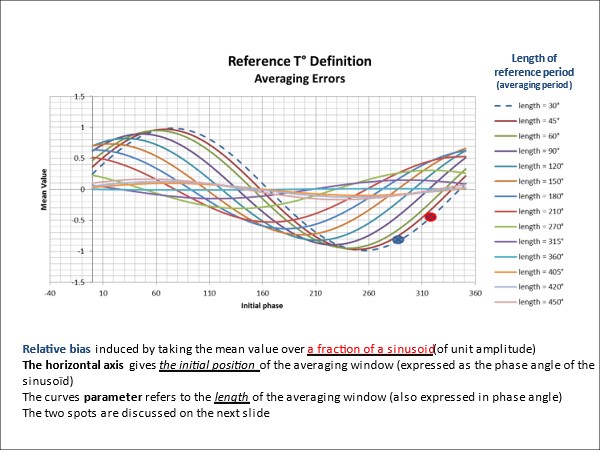Abbildung 13: Verzerrung des zur Berechnung der Anomalien verwendeten Basiswerts nach Länge der Referenzperiode. Die Periode der Sinuskurve mit Einheitsamplitude wird in Grad (360°) ausgedrückt. Die Kurven stellen die Länge der Referenzperioden dar, die für die Berechnung der Anomalien verwendet wurden. Sie sind ebenfalls in Grad angegeben (die Bruchteile der Periode darstellen). Die Punkte der verschiedenen Kurven entsprechen dem anfänglichen Offset der Referenzperiode. Diese Verzerrungen sind sehr variabel und können bis zur Amplitude der Sinuskurve reichen. In dieser Abbildung wird auch das Problem der „gestuften Verbindung“ deutlich, wenn man von einer Referenzperiode zu einer anderen wechselt, wobei sich die Verzerrung je nach Position auf der Sinuskurve in die eine oder andere Richtung ändert. Die beiden Punkte, die den Kurven hinzugefügt wurden, veranschaulichen dieses Problem.

Um unsere Beschwerden zusammenzufassen, können wir einfach sagen, dass die Verwendung von Temperaturanomalien ein dreifaches „mathematisches“ Problem darstellt: Sie führt zu falschen Trends, Verzerrungen und verursacht Verbindungsprobleme, wenn man von einem Bezugsfenster zum anderen wechselt (1930-1960, 1960-1990 und möglicherweise 1990-2020, um die WMO- und IPCC-Konvention zu verwenden, die nicht die der NASA ist; letztere beginnt ihren ersten Bezugszeitraum zum Zeitpunkt des Starts der ersten Wettersatelliten, was zwar logisch ist, aber zur Verwirrung beiträgt).

Zuverlässigkeit lokaler Messungen

Nachdem die Gefahren aufgezeigt worden sind, die sich aus der Verwendung globaler oder lokaler Temperaturanomalien ergeben, muss auch die Qualität der „rohen“ Einzelmessungen hinterfragt werden, wie sie in den „primären“ Datenbanken erfasst und aufgezeichnet werden, aus denen die monatlichen und jährlichen Durchschnittswerte und ihre Anomalien extrahiert werden.

Die Temperatur im Tagesverlauf

Die Temperatur schwankt im Laufe des Tages mit einer Amplitude, die von der lokalen Bewölkung abhängt, die tagsüber als Abschirmung und nachts als Abdeckung wirkt. Je stärker die Bewölkung ist, desto geringer ist die Amplitude der Tag-Nacht-Temperaturschwankungen. Bei Abwesenheit von Wolken können die täglichen Temperaturschwankungen beispielsweise in den europäischen Gebirgen 20°C überschreiten. Es stellt sich daher die Frage, welche Temperatur für einen bestimmten Tag repräsentativ ist. In der Tat gibt es verschiedene Methoden (Maximum + Minimum / 2, Durchschnitt der zu bestimmten Zeiten aufgezeichneten Temperaturen, kontinuierliche Ablesung und Durchschnitt der Messungen usw.), und diese Methoden werden nicht immer erläutert. Dies stellt eine erste Fehlerart dar (Abbildung 14).

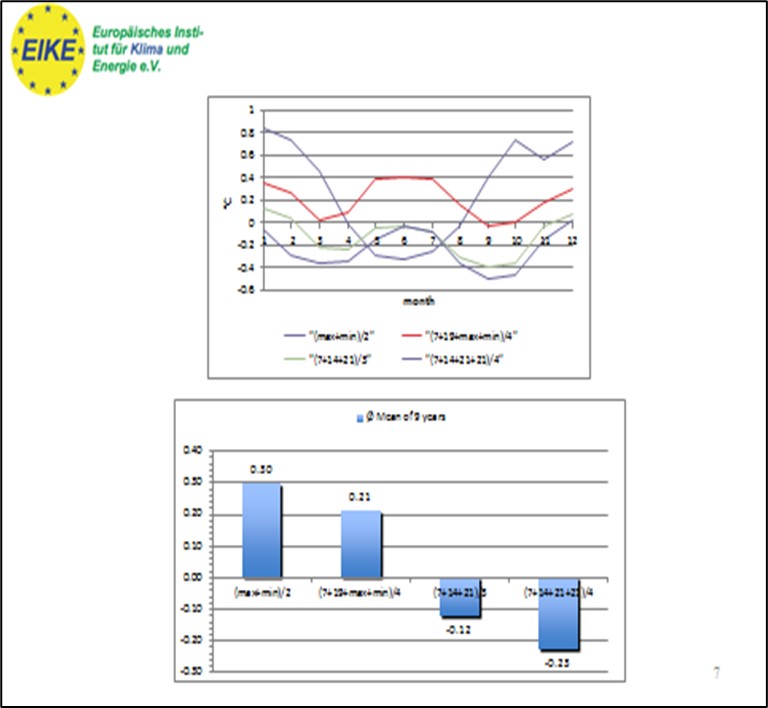Abbildung 14: Algorithmen zur Bestimmung der Tagestemperatur und Fehler im Vergleich zur tatsächlichen Durchschnittstemperatur, die durch die Integration kontinuierlicher Temperaturmessungen über die gesamten 24 Stunden eines Tages abgeleitet wird. Der Fehler liegt in der Größenordnung von +- 0,6°C

Terrestrische Untersuchungen

Die längsten mit dem Thermometer aufgezeichneten Messreihen sind etwa 300 Jahre alt. Die Bedingungen normalisierten sich allmählich und erreichten ihren Höhepunkt in den Stevenson-Wetterhütten. Diese wurden später und nach und nach durch gekapselte Sensoren (Thermistor-Thermoelemente oder Platin-Filament-Thermometer) ersetzt, die jeweils eine Neukalibrierung erforderten. Auch die Umgebung dieser Sensoren hat sich im Laufe der Zeit durch Urbanisierung, Pflasterung usw. verändert („städtischer Blockeffekt“). Viele dieser Sensoren befinden sich heute in unmittelbarer Nähe von Gebäuden, die Sonnenstrahlung sammeln oder reflektieren, manchmal in der Nähe von Klimaanlagen. außer auf dem Rollfeld des Flughafens in Reichweite von Flugzeugabgasen und anderen auf den Start- und Landebahnen manövrierenden Fahrzeugen. Basierend auf einer großen Umfrage von Antony Watts (von der Website WattsUpWithThat) wurde geschätzt, dass nur 10 % der Installationen auf amerikanischem Boden einen Messfehler von weniger als 1 °C aufweisen (Abbildung 15).

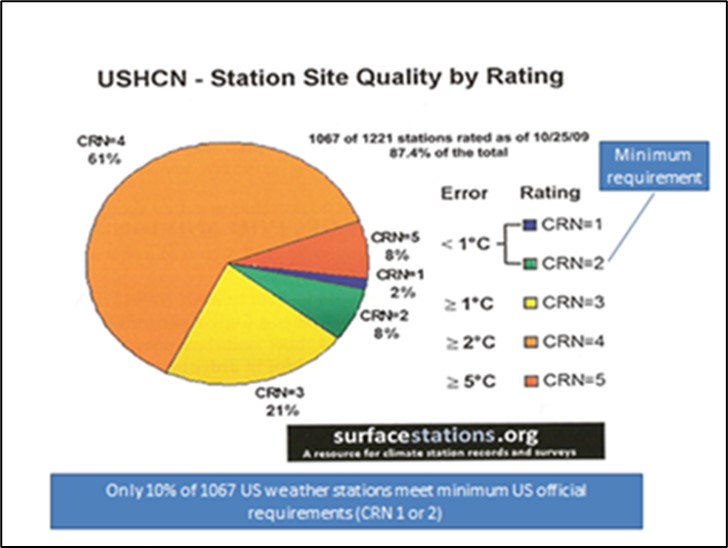Abbildung 15. Genauigkeit der Messungen an terrestrischen Wetterstationen in den USA. Weniger als 10% der 1221 untersuchten Stationen haben einen Fehler von weniger als 1°C.

Für andere Länder liegen keine Daten vor, aber man kann davon ausgehen, dass das Ergebnis vergleichbar, wenn nicht sogar schlechter sein wird. Darüber hinaus muss eine Höhenkorrektur des Messpunktes vorgenommen werden, um alle Temperaturen auf Meereshöhe zurückzubringen. Diese Korrektur ist rein theoretisch und basiert auf einer adiabatischen Ausdehnung in der Atmosphäre, was aber fast nie zutrifft, wie die Messungen der Wetterballone beweisen.

Wir haben es also mit mehreren voneinander unabhängigen Fehlern zu tun, die häufig willkürlich und undurchsichtig von Hand korrigiert werden und die sich häufen.

Wetterstationen sind sehr nützlich, um lokale Bedingungen zu beschreiben und kurzfristige Vorhersagen zu machen, aber wegen der Fehler, welche die dort möglichen Messungen verfälschen, überhaupt nicht geeignet, um lokale Temperaturschwankungen in der Größenordnung von einem Hundertstel Grad pro Jahr festzustellen, wie es der IPCC behauptet.

Wird fortgesetzt. Wer den gesamten Bericht sofort lesen will, findet ihn als pdf hier

IPCC has it all wrong Li-Edition Deutsch