Der Fehler des Mittelwertes: ein Disput zwischen Gavin Schmidt und Nicola Scafetta
Und schon wieder schreiben wir über die richtige Verwendung von Statistiken in der Klimawissenschaft. Traditionell werden die schwerwiegendsten Fehler bei der statistischen Analyse in den Sozialwissenschaften begangen, dicht gefolgt von medizinischen Arbeiten. Die Klimawissenschaft heftet sich an ihre Fersen.
In diesem Fall handelt es sich um einen Streit zwischen Nicola Scafetta, Professor für Atmosphärenphysik an der Universität Neapel, und Gavin Schmidt, Blogger bei RealClimate.org, Klimamodellierer und Direktor des Goddard Institute for Space Studies (GISS) der NASA.
Scafettas Originalarbeit aus dem Jahr 2022, veröffentlicht in den Geophysical Research Letters, ist der Ursprung des Streits (das Herunterladen der pdf-Datei ist kostenlos). Die Kernaussage der Studie lautet, dass CMIP6-Klimamodelle (GCMs), die eine ECS (Equilibrium Climate Sensitivity) von mehr als 3°C/2xCO₂ („°C/2xCO₂“ bedeutet °C pro CO₂-Verdoppelung) erzeugen, statistisch signifikant von den Beobachtungen seit 1980 abweichen (sie laufen zu heiß). Dieses Ergebnis ist nicht überraschend und steht im Einklang mit den jüngsten Ergebnissen von McKitrick und Christy (2020). Die Tatsache, dass die AR6/CMIP6-Klimamodelle zu heiß laufen und dass dies eine Funktion einer zu hohen ECS zu sein scheint, wird im AR6 eingeräumt:
„Der AR5 bewertete mit geringem Vertrauen, dass die meisten, wenn auch nicht alle CMIP3- und CMIP5-Modelle den beobachteten Erwärmungstrend in der tropischen Troposphäre während des Satellitenzeitraums 1979-2012 überschätzten, und dass ein Drittel bis die Hälfte dieser Differenz auf eine Überschätzung des SST-Trends (Meerestemperatur) während dieses Zeitraums zurückzuführen war. Seit dem AR5 zeigen zusätzliche Studien auf der Grundlage von CMIP5- und CMIP6-Modellen, dass diese Erwärmungsverzerrung bei den troposphärischen Temperaturen bestehen bleibt.“ – (AR6, S. 443)
Und:
„Mehrere Studien, die CMIP6-Modelle verwenden, deuten darauf hin, dass Unterschiede in der Klimasensitivität ein wichtiger Faktor sein könnten, der zu der Diskrepanz zwischen den simulierten und beobachteten troposphärischen Temperaturtrends beiträgt (McKitrick und Christy, 2020; Po-Chedley et al., 2021)“ – (AR6, S. 443)
Die AR6-Autoren versuchten, das Eingeständnis durch geschickte Formulierungen abzuschwächen, aber McKitrick und Christy zeigten, dass die AR5/CMIP5-Modelle in der tropischen Troposphäre zu warm sind und die Beobachtungen auf statistisch signifikantem Niveau nicht übereinstimmen. Doch ungeachtet der Beweise, dass AR5 bereits zu warm war, ist AR6 noch wärmer, wie im AR6 auf Seite 321 zugegeben wird:
„Die Schätzung des AR5 für die historische Erwärmung zwischen 1850-1900 und 1986-2005 beträgt 0,61 [0,55 bis 0,67] °C. Das Äquivalent im AR6 beträgt 0,69 [0,54 bis 0,79] °C, und die Differenz von 0,08 [-0,01 bis 0,12] °C ist eine Schätzung des Beitrags von Veränderungen im Beobachtungswissen allein (kapitelübergreifender Kasten 2.3, Tabelle 1).“ – (AR6, S. 321).
Wir sehen also, dass die AR6-Einschätzung, wonach die AR6- und AR5-Klimasensitivität für CO₂ zu hoch sein könnte und dass AR6 schlechter ist als AR5, die Arbeit unterstützt, die Scafetta, McKitrick und Christy in den letzten Jahren geleistet haben.
Betrachten wir nun den Streit zwischen Scafetta und Schmidt darüber, wie der statistische Fehler der mittleren Erwärmung von 1980-1990 bis 2011-2021 zu berechnen ist. Schmidts (2022) Einwände gegen Scafettas Fehleranalyse sind hier in seinem Blog veröffentlicht. Scafettas ursprünglicher Artikel in Geophysical Research Letters wurde später durch einen ausführlicheren Artikel in Climate Dynamics (Scafetta N., 2022b) ergänzt, in dem das Problem im ersten und zweiten Anhang ausführlich erörtert wird.
Scafettas (2022a) Analyse der Klimamodelle ECS
Der Kern von Scafettas Argumentation ist in Abbildung 1 dargestellt:

Abbildung 1. Die Ergebnisse der Klimamodelle sind in rot und die Beobachtungen der ECMWF ERA5 Wetter-Reanalyse in blau dargestellt. Die beiden oberen Diagramme zeigen Modellläufe, die zu ECS-Berechnungen von mehr als 3°C/2xCO₂ führen, und das untere Diagramm jene mit ECS von weniger als 3°C/2xCO₂. Diagramm aus (Scafetta N., 2022a)
In Abbildung 1 sehen wir, dass die Modelle heiß laufen, wenn ECS größer als 3°C/2xCO2 ist. Die Diagramme auf der rechten Seite zeigen einen Vergleich der mittleren Differenz zwischen den Beobachtungen und den Modellen in den 11-Jahres-Zeiträumen 1980-1990 und 2011-2021. Scafettas vollständige Analyse aus dem Jahr 2022a ist in Tabelle 1 enthalten, in der 107 durchschnittliche CMIP6-GCM-Simulationen für die von Climate Explorer bereitgestellten IPCC-Treibhausemissionsszenarien Historisch + SSP2-4.5, SSP3-7.0 und SSP5-8.5 analysiert werden. Die ERA5-T2m [1] mittlere globale Oberflächenerwärmung von 1980-1990 bis 2011-2021 wurde anhand des weltweiten ERA5-Gitters auf 0,578°C geschätzt. Die mittlere Erwärmung der IPCC/CMIP6-Klimamodelle ist bei allen dargestellten Modellen deutlich höher, wenn der ECS größer als 3°C/2xCO₂ ist.
Schmidts Analyse
Die rechts in Abbildung 1 dargestellten Diagramme sind der Kern der Debatte zwischen Scafetta und Schmidt. Die von Schmidt aufgezeichneten Daten (in unserer Abbildung 2) unterscheiden sich geringfügig, zeigen aber das Gleiche.
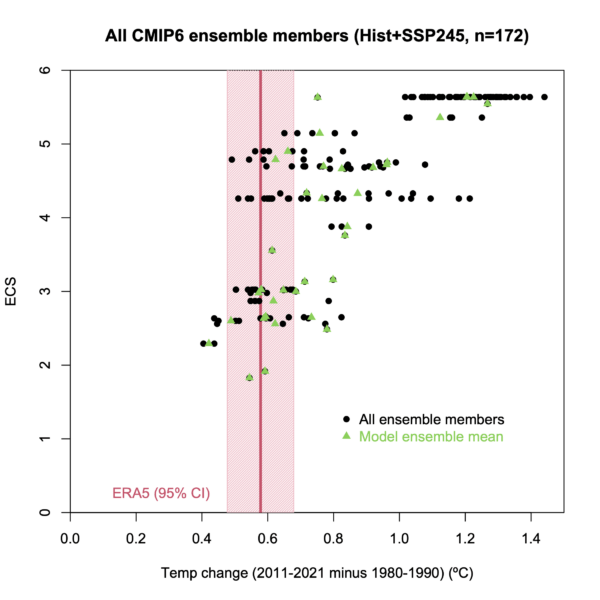
Abbildung 2. Schmidts Diagramm des IPCC/CMIP6 modellierten ECS im Vergleich zu den Beobachtungen der ERA5-Reanalyse. Die grünen Punkte sind die Mittelwerte des Modell-Ensembles, die in Scafettas Darstellung (Abbildung 1) verwendet wurden, und die schwarzen Punkte sind einzelne Modellläufe. Das rosa Band ist Schmidts Berechnung der Unsicherheit der ERA5-Beobachtungen.
In Abbildung 2 sehen wir, dass die einzigen ECS-Ensemblemittelwert-Schätzungen (grüne Punkte), die mit der mittleren Differenz der ERA5-Wetter-Reanalyse zwischen 1980-1990 und 2011-2021 übereinstimmen oder um diese herum liegen, ECS-Schätzungen von 3°C/2xCO₂ oder weniger sind. Alle Ensemble-ECS-Schätzungen über 3°C/2xCO₂ sind zu hoch. Bei den Basisdaten stimmt Schmidt also mit Scafetta überein, was hilfreich ist.
Der Disput
Der Kern des Streits ist die Frage, wie die 95%ige Unsicherheit (die Fehlerschätzung) des ERA5-Mittelwerts der Wetter-Reanalyse 2011-2021 im Vergleich zum Zeitraum 1980-1990 berechnet werden kann. Diese Fehlerschätzung wird verwendet, um zu entscheiden, ob ein bestimmtes Modellergebnis innerhalb der Fehlermarge der Beobachtungen (ERA5) liegt oder nicht. Scafetta berechnet einen sehr kleinen ERA5-Fehlerbereich von 0,01 °C (Scafetta N. , 2022b, Anhang) aus ähnlichen Produkten (z. B. HadCRUT5), da das ECMWF (Europäisches Zentrum für mittelfristiges Wetter) mit seinem Wetter-Reanalyseprodukt (ERA5) keine Unsicherheitsabschätzung bereitstellt, so dass er geschätzt werden muss. Schmidt berechnet eine sehr große ERA5-Fehlerspanne von 0,1°C unter Verwendung der ERA5-Standardabweichung für den Zeitraum. Sie ist in Abbildung 2 als rosa Band dargestellt. Dies ist der kritische Wert, um zu entscheiden, welche Unterschiede zwischen den Klimamodell-Ergebnissen und den Beobachtungen statistisch signifikant sind.
Wenn wir davon ausgehen, dass Scafettas Schätzung korrekt ist, zeigen die Abbildungen 1 und 2, dass alle Klimamodell-Simulationen (die grünen Punkte in Abbildung 2) für die 21 Klimamodelle mit ECS >3°C und die große Mehrheit ihrer Simulationsmitglieder (die schwarzen Punkte) offensichtlich auf statistisch signifikantem Niveau zu warm sind. Unter der Annahme, dass Schmidts Schätzung korrekt ist, deutet Abbildung 2 darauf hin, dass drei Klimamodelle mit ECS>3°C teilweise innerhalb der ERA5-Fehlerspanne liegen, während die anderen 18 Klimamodelle zu warm sind.
Obwohl Schmidts Ergebnis die Schlussfolgerung von Scafetta (2022a, 2022b), dass nur die Klimamodelle mit ECS<3,01°C die Erwärmung von 1980-1990 bis 2011-2021 am besten nachzuprojizieren scheinen, nicht wesentlich zu ändern scheint, ist es wichtig, die Fehlerfrage zu diskutieren. Ich beziehe mich dabei auf die stochastischen Standardverfahren zur Bewertung des Fehlers des Mittelwerts, die in dem klassischen Lehrbuch zur Fehleranalyse von Taylor (1997) diskutiert werden.
Im Folgenden wiederhole ich die von Schmidt vorgenommenen Berechnungen und kommentiere sie unter Verwendung des HadCRUT5.0.1.0-Jahresmittelwertes der globalen Temperatur anstelle des ERA5-T2m, weil er leichter zu bekommen ist, weil er dem ERA5-T2m nahezu gleichwertig ist und vor allem, weil er auch die relativen stochastischen Unsicherheiten für jedes Jahr angibt, was, wie bereits erläutert, eine entscheidende Komponente für die Bewertung der statistischen Signifikanz von Unterschieden zwischen der Realität und den Klimamodellen ist.
Schmidts Schätzung des Fehlers des Mittelwerts (der rosafarbene Balken in Abbildung 2) liegt bei ± 0,1°C (95%ige Sicherheit). Diesen Wert erhielt er, indem er davon ausging, dass die zwischenjährlichen Schwankungen im ERA5-T2m von 2011 bis 2021 gegenüber dem dekadischen Mittelwert zufälliges Rauschen sind. In der Praxis berechnete er die durchschnittliche Erwärmung (0,58 °C) von 2011 bis 2021 anhand der ERA5-T2m-Temperaturanomalien im Verhältnis zum Mittelwert von 1980-1990. Das heißt, er hat die Werte auf den Mittelwert von 1980-1990 „gestützt“. Dann schätzte er den Fehler des Mittelwerts, indem er die Standardabweichung der Basiswerte von 2011 bis 2021 berechnete, diese Standardabweichung durch die Wurzel aus 11 teilte (weil es N=11 Jahre gibt) und schließlich das Ergebnis mit 1,96 multiplizierte, um die 95%ige Sicherheit zu erhalten. Hier kann man eine Tabellenkalkulation herunterladen, die Schmidts und Scafettas Berechnungen durchführt.
Abbildung 3 zeigt die Gleichung von Schmidt für den Fehler des Mittelwerts. Wenn dieser Wert mit 1,96 multipliziert wird, um die 95%ige Sicherheit zu erhalten, ergibt sich ein Fehler von ± 0,1°C:
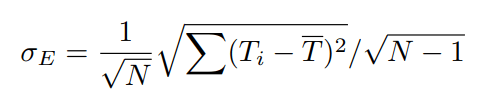
Abbildung 3. Die von Schmidt verwendete Gleichung zur Berechnung des Fehlers des Mittelwerts für die ERA5-Daten.
Die von Schmidt verwendeten Gleichungen sind diejenigen, die in Taylor (1997, Seiten 100-102) aufgeführt sind. Das Hauptproblem bei Schmidts Ansatz ist, dass Taylor deutlich erklärt, dass die Gleichung in Abbildung 3 für den Fehler des Mittelwerts nur dann funktioniert, wenn die N jährlichen Temperaturwerte (Ti) zufällige „Messungen der gleichen Größe x“ sind. Beispielsweise verwendet Taylor (Seite 102-103) die obige Gleichung zur Schätzung des Fehlers des Mittelwerts für die elastische Konstante k „einer“ Quelle unter Verwendung wiederholter Messungen mit dem gleichen Instrument. Da die wahre Elastizitätskonstante nur ein Wert ist, kann die Variabilität der wiederholten Messungen als zufälliges Rauschen um einen Mittelwert interpretiert werden, dessen Standardabweichung die Standard Deviation of the Mean (SDOM) ist.
Bei der Verwendung der SDOM gehen Schmidt et al. implizit davon aus, dass jeder Jahresmittelwert der Temperatur eine Messung eines einzigen wahren dekadischen Wertes ist und dass der statistische Fehler für jeden Wert durch seine Abweichung von diesem dekadischen Mittelwert gegeben ist. Sie gehen also davon aus, dass die „wahre“ globale Oberflächentemperatur zwischen 1980 und 1990 oder 2011-2021 nicht schwankt und alle Abweichungen vom Mittelwert (oder wahren Wert) zufällige Schwankungen sind.
Die interannuelle Variabilität der globalen Temperaturen in diesen zwei Jahrzehnten ist jedoch kein zufälliges Rauschen um einen dekadischen Mittelwert. Die N Jahresmitteltemperaturmessungen von 2011 bis 2021 sind keine unabhängigen „Messungen der gleichen Größe x“, sondern jedes Jahr herrscht ein anderer physikalischer Zustand des Klimasystems. Dies ist in der Darstellung der beiden Jahrzehnte in dieser Tabelle leicht zu erkennen. Die x-Achse ist mit 2010-2022 beschriftet, aber für die orangefarbene Linie ist es eigentlich 1979-1991. Nach Taylor (1997) ist SDOM also nicht die richtige Gleichung für diesen speziellen Fall.
Wie Scafetta (2022b) erklärt, ist die Aufzeichnung der globalen Temperatur hochgradig autokorreliert, da sie die dynamische zwischenjährliche Entwicklung des Klimasystems enthält, die durch ENSO-Oszillationen und andere natürliche Phänomene hervorgerufen wird. Diese Oszillationen und Trends sind ein physikalisches Signal und kein Rauschen. Scafetta (2022b) erklärt, dass bei einer generischen Zeitreihe (yt), die von Gauß- (zufällig) verteilten Unsicherheiten ξ mit Standardabweichung σξ betroffen ist, der Mittelwert und der Fehler des Mittelwerts durch die Gleichung in Abbildung 4 gegeben sind:
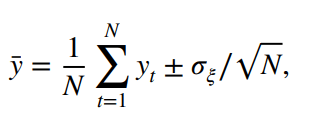
Abbildung 4. Die richtige Gleichung zur Berechnung der Unsicherheit im Mittelwert der globalen Temperatur über einen Zeitraum, in dem sich der Mittelwert ändert.
Die Gleichung in Abbildung 4 ergibt einen Fehler von 0,01°C (bei einem Konfidenzniveau von 95 %; Einzelheiten zur Berechnung findet man in der Tabelle hier). Wenn die Standardabweichung der Fehler nicht streng konstant für jedes Datum ist, ist der in der obigen Gleichung zu verwendende Standardfehler die Quadratwurzel aus dem Mittelwert der quadrierten Unsicherheiten für jedes Datum.
Scafettas Gleichung leitet sich direkt von der allgemeinen Formel für die Fehlerfortpflanzung ab, die von (Taylor, 1997, S. 60 und 75) diskutiert wird. Taylor erklärt, dass die Gleichungen auf den Seiten 60 und 75 für die Schätzung des Fehlers einer Funktion „mehrerer“ unabhängiger Variablen übernommen werden müssen, von denen jede mit einem individuellen stochastischen Fehler behaftet ist, der verschiedenen physikalischen Zuständen entspricht, wie z. B. dem Durchschnitt einer globalen Temperaturaufzeichnung von N „verschiedenen“ Jahren. Die Unsicherheit der Funktion (z. B. der Mittelwert von N verschiedenen Größen) hängt nur von dem statistischen Fehler jeder Größe ab, nicht aber von der Variabilität der verschiedenen Größen gegenüber ihrem Mittelwert.
Wir können ein im Internet verfügbares Tool zur Berechnung der Fehlerfortpflanzung verwenden, um unsere Berechnungen zu überprüfen. Ich habe die Jahresmittelwerte der HadCRUT5-Temperaturdaten mit ihren relativen Unsicherheiten hochgeladen und den Rechner den Mittelwert mit seinem relativen Fehler bewerten lassen. Das Ergebnis ist in Abbildung 5 dargestellt.

Abbildung 5. Die richtige Gleichung zur Berechnung der Unsicherheit des Mittelwerts der globalen Temperatur über einen Zeitraum von N=11 verschiedenen Jahren, die durch unterschiedliche jährliche Temperaturmittelwerte gekennzeichnet sind.
Schmidts Berechnung der Standardabweichung des Mittelwerts (SDOM) basiert auf der irrigen Annahme, dass er mehrere Messungen derselben Größe mit dem gleichen Verfahren durchführt und dass daher die zwischenjährliche Abweichung vom dekadischen Mittelwert eine Art zufälliges Rauschen ist, das als stochastische Unsicherheit betrachtet werden kann. Keine dieser Bedingungen ist in diesem Fall erfüllt. Die globale jährliche durchschnittliche Temperaturanomalie ändert sich aus natürlichen Gründen ständig, obwohl ihre jährlichen Schätzungen auch durch einen kleinen stochastischen Fehler wie den in Scafettas Berechnung enthaltenen beeinflusst werden. Laut Taylor sind es nur die Messfehler der jährlichen Temperaturmittelwerte, die den Fehler des 11-Jahres-Mittelwerts von 2011 bis 2021 bestimmen können.
Wie Scafetta im Anhang zu Scafetta 2022b schreibt, enthält der globale Temperaturdatensatz von HadCRUT5 seine 95%-Konfidenzintervall-Schätzung, und von 2011 bis 2021 betragen die Unsicherheiten für die monatlichen und jährlichen Mittelwerte monatlich ≈ 0,05°C und jährlich ≈ 0,03°C. Die geschätzte Unsicherheit der Berkeley Earth Land/Ozean-Temperaturaufzeichnungen beträgt 0,042°C (monatlich), 0,028°C (jährlich) und 0,022°C (dekadisch). Je länger der Zeitraum ist, desto geringer ist der Fehler des Mittelwerts.
Jeder der oben genannten Werte, Jahr für Jahr, muss gemittelt und durch die Quadratwurzel der Anzahl der Jahre (in diesem Fall 11) geteilt werden, um den Fehler des Mittelwerts zu bestimmen. In unserem Fall beträgt der HadCRUT5-Fehler des Mittelwerts für 2011-2021 0,01°C. Bei dem Verfahren von Scafetta kann der „wahre“ Wert in jedem Jahr variieren, bei dem von Schmidt ist dies nicht der Fall.
Die für die ERA5-Wetter-Reanalyse verwendeten Beobachtungen sind nahezu identisch mit denen, die im HadCRUT5-Datensatz verwendet werden (Lenssen et al., 2019; Morice et al., 2021; Rohde et al., 2020). Wie Morice et al. anmerken, verwendet das MET Office Hadley Centre ERA5 zur Qualitätskontrolle.
Lenssen et al., an denen Gavin Schmidt als Koautor beteiligt ist, nehmen eine umfassende Überprüfung der Unsicherheit verschiedener globaler Durchschnittstemperatur-Datensätze, einschließlich ERA5, vor. Craigmile und Guttorp stellen in Abbildung 6 den geschätzten jährlichen Standardfehler in mehreren globalen Temperaturdaten dar: GISTEMP, HadCRUT5, NOAA, GISS, JMA und Berkeley Earth:
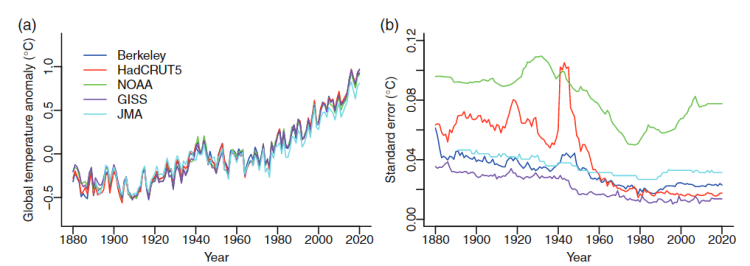
Abbildung 6. Gesamt-Usicherheit für drei globale Temperaturanomalie-Datensätze. Diese Datensätze sollten eine ähnliche Unsicherheit aufweisen wie ERA5. Quelle: (Craigmile & Guttorp, 2022).
Abbildung 6 zeigt, dass der Standardfehler der Unsicherheiten von 1980 bis 2021 auf der Jahresskala und mit 95 % Konfidenz sehr viel geringer ist als der Schmidtsche Fehler des Mittelwerts von 0,10 °C, der zudem auf einer Zeitskala von 11 Jahren berechnet wird. Die in Abbildung 6 angegebenen Unsicherheiten sind nicht durch die interannuelle Temperaturvariabilität um ein dekadisches Mittel gegeben. Dieses Ergebnis zeigt deutlich, dass Schmidts Berechnung fehlerhaft ist, denn auf der 11-Jahres-Skala muss der Fehler des Mittelwerts deutlich kleiner sein (durch die Wurzel aus 11 = 3,3) als der jährliche Wert.
Scafetta (2022b) argumentiert, dass die Fehler für den Jahresmittelwert von ERA5-T2m in der gleichen Größenordnung liegen sollten wie die Fehler anderer Temperatur-Rekonstruktionen, etwa des eng verwandten HadCRUT5-Datensatzes. Daher muss der Fehler auf der dekadischen Skala vernachlässigbar sein, etwa ±0,01°C, und dieses Ergebnis wird auch durch die Online-Rechner-Tools zur Schätzung des Fehlers von gegebenen Funktionen unabhängiger Variablen bestätigt, wie in Abbildung 5 gezeigt.
Die Unterschiede zwischen Scafetta und Schmidt sind auf die unterschiedlichen Schätzungen des ERA5-Fehlers zurückzuführen. Ich halte die Schätzungen von Scafetta für wesentlich realistischer.
Patrick Frank helped me with this post, but any errors are mine alone.
Download the bibliography here.
- ERA-T2m is the European Centre for Medium-Range Weather (ECMWF) Reanalysis 2-meter air temperature variable. Link. ↑
Übersetzt von Christian Freuer für das EIKE