Das LWIR-Puzzle*: Experimente mit dem MODTRAN-Modell
Kevin Kilty
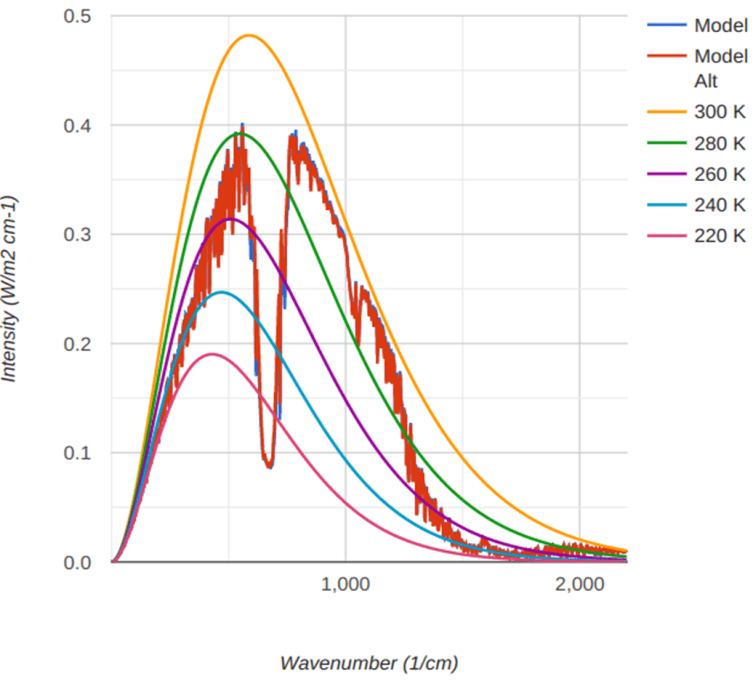
Abbildung 1. Unterschiede in der ausgehenden langwelligen Strahlung (OLR) an der Spitze einer tropischen Atmosphäre zwischen 260 ppm und 420 ppm CO₂-Konzentration. Die einzigen offensichtlichen Unterschiede liegen in der Nähe des atmosphärischen Wasserdampffensters.
Auf dieser Website wird viel Tinte über CO₂ und seine Auswirkungen auf die langwellige Infrarotstrahlung (LWIR) verschüttet, sowohl in den Artikeln selbst als auch in den nachfolgenden Threads. Da diese Seite von vielen Skeptikern des Zusammenhangs zwischen CO₂ und globaler Erwärmung besucht wird, versuchen die meisten dieser Argumente, CO₂ als Ursache für eine Klimaerwärmung zu entlasten.
Ein gemeinsames Thema ist, dass die relativ geringe Auswirkung einer CO₂-Verdoppelung auf das LWIR an der Oberseite der Atmosphäre (TOA) zu gering zu sein scheint, um die viel größere Wirkung zu erzielen, die für eine Erwärmung von 3 K an der Oberfläche erforderlich ist. In mehreren Artikeln vom letzten Sommer wurden die Behauptungen des IPCC gegenüber dem Stefan-Boltzmann-Gesetz in Frage gestellt;[1][2] und viele Kommentare spiegeln diese Meinung ebenfalls wider. Es scheint ein allgemeines Missverständnis zu geben, das von der Gemeinschaft der Klimaforscher selbst initiiert wurde und bis heute aufrechterhalten wird. Untersuchen wir das Problem des Infrarottransports in der Atmosphäre anhand einiger einfacher Modellierungen. Einige dieser Ergebnisse könnten für so Manchen überraschend sein.
[Hervorhebung im Original]
Die Essenz eines Missverständnisses
Wenn die CO₂-Konzentration von ihrem derzeitigen Wert von 400 ppm auf 800 ppm verdoppelt wird, führt dies zu einer Verringerung der ausgehenden LWIR-Strahlung um etwa 3,7 W/m² am TOA.[3] Fast jeder spricht bei diesem Rückgang von einem „Forcing“. Diese unglückliche Formulierung erweckt den Eindruck, dass sich die 3,7 W/m² an der TOA mit der Sonnenstrahlung, die auf die Oberfläche trifft, verbinden und die Oberflächentemperatur direkt nach oben treiben. Er suggeriert, wenn man so will, so etwas wie einen Wärmestromvektor, der auf die Oberfläche zeigt.
Dies ist jedoch nicht der Fall. Das Defizit von 3,7 W/m² strahlt überhaupt nicht vom TOA auf die Oberfläche. Es handelt sich um ein Defizit der ausgehenden Strahlung, das durch die höhere CO₂-Konzentration auf allen Ebenen der Atmosphäre verursacht wird, die mehr Strahlung absorbiert und effektiver in alle Richtungen abstrahlt. Der Wert von 3,7 W/m² an der TOA hängt von der angenommenen Temperatur und Zusammensetzung der Atmosphäre ab.
In der Nähe der Erdoberfläche verhält es sich ähnlich. Das LWIR wird in dieser Atmosphäre aufgrund unserer neuen CO₂-Konzentration anders absorbiert und emittiert. Da die Atmosphäre für LWIR relativ undurchlässig ist (allerdings nicht völlig undurchlässig; verschiedene Modelle gehen von 12 % bis 35 % Transparenz in der Spalte von der Oberfläche bis zum TOA aus), hat das, was am TOA geschieht, nur begrenzte Auswirkungen auf das, was an der Oberfläche geschieht. Was an der Oberfläche zählt, ist hauptsächlich die Absorption und Emission von LWIR im wärmsten und feuchtesten Teil der Atmosphäre in Bodennähe. Der Klimaantrieb ist die Störung, die CO₂ auf den lokalen LWIR-Transport ausübt; es ist nicht der Rückgang des LWIR um 3,7 W/m², den wir aufgrund dieser Störung zufällig am TOA beobachten können.
Strahlungstransport
Die Übertragung von Strahlungsenergie ist ein komplexes Problem. Häufig wird allein die Stefan-Boltzmann-Gleichung als Grundlage für Strahlungsberechnungen verwendet. Dies funktioniert nur, wenn die Strahlung zwischen Oberflächen ausgetauscht wird, zwischen denen sich kein IR-aktives Medium befindet. Mit anderen Worten: Die alleinige Verwendung des Stefan-Boltzmann-Gesetzes schränkt die Probleme, die man legitimerweise angehen kann, stark ein.
Wenn eine physikalische Situation Grenzen mit fester Temperatur oder festem Strahlungsfluss und ein Medium umfasst, das durch Emission, Absorption oder Streuung an der Übertragung teilnehmen kann, wird das Problem enorm schwieriger und erfordert einen echten Lösungsansatz für den Strahlungstransport. Das einzige Tool, das mir zur Verfügung steht, ist MODTRAN, das den Transport zwischen zwei Punkten im Raum berechnen kann, solange Temperatur und Zusammensetzung angegeben sind. Es kann keine unbekannte Temperatur berechnen, weil es kein vollständiger Lösungsansatz für die Transportgleichung ist.
Das Problem des Strahlungstransports sieht folgendermaßen aus: Strahlung, die an einem beliebigen Punkt im Raum einfällt, hat den Raum auf Strahlen von anderen Punkten durchquert, an denen es zu Absorption, Emission und Streuung gekommen ist. Inzwischen entsteht an jedem Punkt aufgrund seiner Temperatur eine gewisse Menge an emittierter Strahlung, die sich in alle Richtungen ausbreitet. MODTRAN berechnet die akkumulierten Änderungen der Strahlungsintensität entlang einer bestimmten Bewegungsrichtung aus all diesen Faktoren.
Dieses Problem ist fast identisch mit dem der Berechnung des Neutronenflusses in einem Kernreaktor, der Wärme abgibt, Elemente umwandelt und dabei weitere Neutronen aussendet. Ohne eine Transportgleichung würde man nie verstehen, was in einem Reaktor vor sich geht, und dasselbe gilt für den Transport von Strahlungswärme in einer aktiven Atmosphäre.
Grenzen des MODTRAN-Modells
Die an der Universität von Chicago verfügbare Version von MODTRAN besteht aus einem in den 1980er Jahren geschriebenen FORTRAN-Programm, auf das man über einen in einer anderen Sprache geschriebenen „Wrapper“ in begrenztem Umfang zugreifen kann. Der Wrapper bietet eine grafische Benutzeroberfläche (GUI) mit Eingabefeldern, in denen man die Randtemperaturen ändern, aus einer begrenzten Anzahl von Atmosphärenmodellen auswählen und den Gehalt an Treibhausgasen oder die Wolkenbedeckung einstellen kann. Das ist praktisch, verhindert aber, dass man die volle Leistung des alten FORTRAN-Codes nutzen kann.
Zum einen kann man nicht in jedem beliebigen Blickwinkel wählen. Nur vertikale Ansichten sind erlaubt. Um die Strahlungsintensität (I) entlang eines vertikalen Pfades in die tatsächliche Bestrahlungsstärke (Fluss) auf einer Oberfläche (G) umzuwandeln, geht man in der Regel von isotroper Strahlung aus, was die Umwandlung so einfach macht wie G= pI. [4] Dies ist nicht besonders wichtig, außer dass es Teil einer Liste von Problemen ist [5], die verhindern, dass die Genauigkeit von MODTRAN besser als 5-10 W/m² ist. Unterschiede zwischen Modellen, die sich nur durch ein oder zwei Parameter unterscheiden, sind jedoch wahrscheinlich genauer als dies.
Zweitens tritt bei einer infrarot-aktiven Atmosphäre eine Temperaturdiskontinuität an den Grenzflächen auf [6], wodurch ein Konzept wie die Oberflächentemperatur mehrdeutig wird. Es erschwert die Einbeziehung der konvektiven Wärmeübertragung in ein Problem.
Drittens habe ich, nachdem ich viele Modelle ausgeführt habe, einen Fehler im alten FORTRAN-Code festgestellt. Der Fehler manifestiert sich in getrennten Durchläufen mit unterschiedlichen Parametern, die zu genau denselben Lösungen führen – und ich meine genau. Das ist ein Fehler. Vor vierzig Jahren wurde ich dafür bezahlt, alte FORTRAN-Codes aus dem gleichen Jahrgang wie MODTRAN umzuschreiben, um sie zwischen Maschinen mit unterschiedlichen Wortlängen, unterschiedlichen Sprachen und unterschiedlichen Compilern zu portieren. Genau wie MODTRAN stammten diese Codes von Bundesverträgen oder Bundesbehörden. Die meisten enthielten eine gewisse Anzahl von Fehlern. Im Falle von MODTRAN scheint der Code an Stellen, an denen er doppelte Genauigkeit verwenden sollte, mit einfacher Genauigkeit zu rechnen.
Benutzer aufgepasst.
Die Auswirkungen von Änderungen der CO₂-Konzentration
MODTRAN bietet mehrere Modelle der Atmosphäre an. Nehmen wir das tropische Modell als Beispiel, und zwar aus dem einfachen Grund, dass ein großer Teil des Sonneneintrags auf die Erde in den Tropen stattfindet. Betrachten wir außerdem die Unterschiede zwischen 260 ppm (vorindustrielle) und 420 ppm (nahezu aktuelle) CO₂-Konzentration. Als Obergrenze der Atmosphäre (Top of Atmosphere, TOA) nehmen wir eine Höhe von 18 km über der Oberfläche von 1013 mbar an. Unser Referenzmodell liegt bei 260 ppm. Es gibt keine Wolken und wir vernachlässigen jegliche Auswirkungen der Konvektion. Ich konzentriere mich ausschließlich auf den Strahlungstransport.
Wie Abbildung 2 zeigt, berechnet MODTRAN die Unterschiede im Strahlungstransport, die durch den von uns gewählten CO₂-Anstieg verursacht werden, als einen Rückgang am TOA von 3 W/m². Die neue Atmosphäre absorbiert mehr LWIR. Diese Abnahme der LWIR-Strahlung würde von Satelliten gemessen werden, aber sie hat sich über 400 Jahre hinweg vollzogen und beträgt nur ein Zehntel Watt pro Quadratmeter und Jahrzehnt. Er ist mit anderen Worten nicht messbar, da er im Rahmen des Auflösungsvermögens eines jeden Instruments und des von der Erde verursachten Rauschens liegt [7].
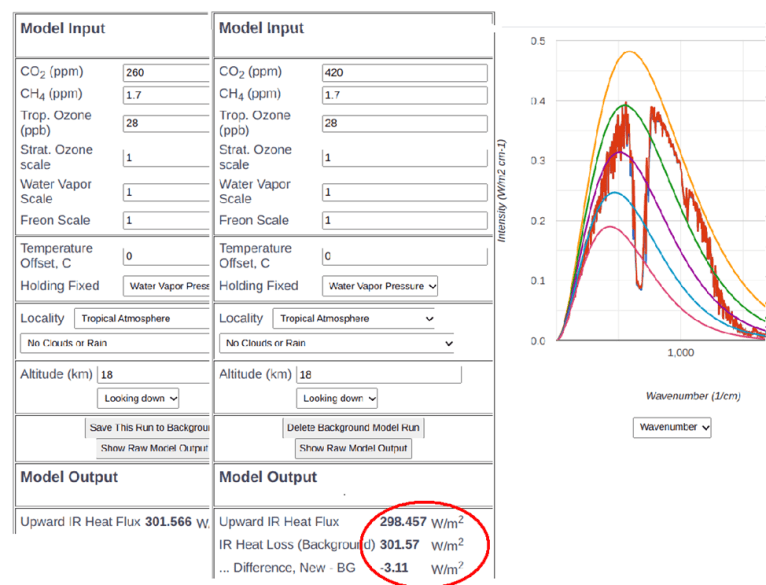
Abbildung 2. Ergebnisse des Referenzmodells und Vergleich mit dem Modell mit höherer CO₂-Konzentration (420 ppm). Beachten Sie, dass die OLR infolge der neuen Absorption in der Atmosphäre zurückgegangen ist.
Das OLR-Diagramm (Abbildung 3) in diesem aktuellen WUWT-Aufsatz [in deutscher Übersetzung hier] zeigt, dass Klimastörungen weitaus größere Auswirkungen haben. Die beiden jüngsten El Ninos und der Pinatubo zum Beispiel zeigen in diesem Diagramm weitaus größere Auswirkungen, als es unser langsamer CO₂-Anstieg jemals könnte. Folglich beweist die Grafik nichts über den gegenwärtigen Einfluss von CO₂.
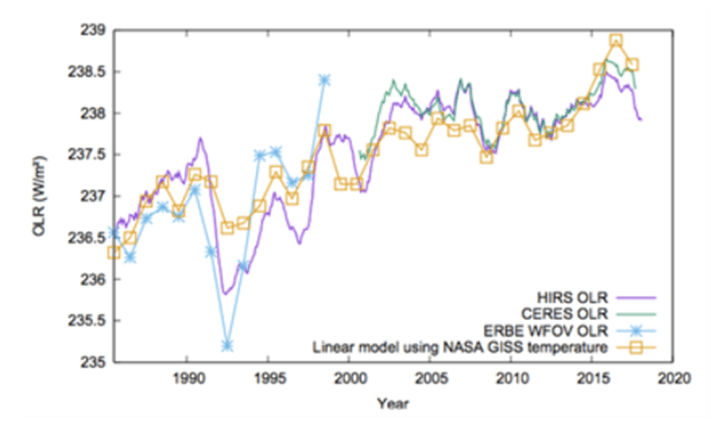
Abbildung 3. Grafik der von Satelliten gemessenen abgehenden langwelligen Strahlung. Vorübergehende Störungen des Klimas wie El Ninos und Vulkanausbrüche machen etwa 1-2 W/m² aus, während der Einfluss von CO₂ in der vorindustriellen Zeit bis heute über die gesamte Grafik hinweg nur etwa 10-20 % ausmachen würde. Diese Grafik stammt aus Dewitte und Clerbaux, 2018, Remote Sensing, 10(10), S.1539 und wurde im oben verlinkten aktuellen WUWT-Aufsatz referenziert.
In der Zwischenzeit erhöht dieser CO₂-Anstieg in der Nähe der tropischen Oberfläche den nach unten gerichteten Fluss um 1 W/m². Wenn wir davon ausgehen, dass sich die tropische Atmosphäre und die Oberfläche in unserem Referenzmodell im Energiegleichgewicht befanden, dann werden die bei 420 ppm berechneten Änderungen des LWIR-Flusses die Temperatur der Atmosphäre und der Oberfläche erhöhen, bis das ausgehende LWIR am TOA wieder den Referenzwert von 301,6 W/m² erreicht. Um herauszufinden, wie hoch der Temperaturanstieg sein muss, um das Gleichgewicht wiederherzustellen, können wir MODTRAN durch eine Reihe von Iterationen verwenden.
Mit Hilfe des Stefan-Boltzmann-Gesetzes können wir berechnen, dass ein Anstieg der langwelligen Strahlung um 1 W/m² an der Oberfläche die Grenztemperatur an der Oberfläche nur um 0,18 K erhöhen würde. Dies ist viel zu wenig, um die Energie am TOA auszugleichen, aber selbst diese kleine Anpassung der Oberflächentemperatur erhöht nicht nur die OLR, sondern auch die abwärts gerichtete LWIR an der Oberfläche erheblich. Wiederholte MODTRAN-Berechnungen mit verfeinerten Schätzungen der Oberflächentemperatur zeigen, dass das Energiegleichgewicht am TOA mit einem Temperaturanstieg von 0,7 K wiederhergestellt ist. Abbildung 4 zeigt dies. Ein Anstieg um 0,7 K an der Oberfläche, die fast schwarz ist (e=0,97), kann jedoch nicht ohne einen Anstieg der emittierten Leistung (berechnet mit dem Stefan-Boltzmann-Gesetz) von 4,2 W/m² aufrechterhalten werden. Das ist ein viel größerer Wert als der, mit dem wir begonnen haben.
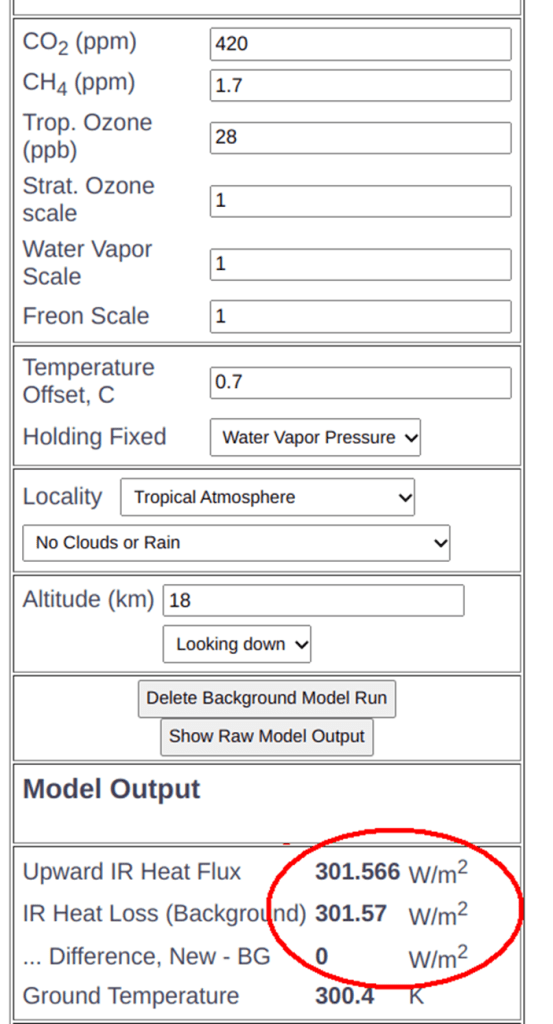
Abbildung 4. Eine Erhöhung der Grenztemperatur um 0,7 K stellt das Energiegleichgewicht am TOA wieder her.
Wie geschieht das? Ein geringer Anstieg der Bestrahlungsstärke an der Bodenoberfläche erhöht deren Temperatur. Dies wiederum erhöht die von der Oberfläche abgestrahlte Leistung. Die erhöhte Strahlungsleistung wird in der Atmosphäre absorbiert, vor allem in der Nähe der Oberfläche, da dies der feuchte Teil der Atmosphäre ist. Ein Teil dieser absorbierten Strahlung wird an den Boden zurückgestrahlt. Dadurch steigt die Oberflächentemperatur wieder leicht an. Der Prozess wiederholt sich ad infinitum. Es handelt sich um eine unendliche Reihe von Wiederabstrahlungen, die schließlich konvergieren, wenn das Energiegleichgewicht wiederhergestellt ist. Unendliche Reihen wie diese sind bei Problemen des Strahlungsaustauschs zwischen Oberflächen mit oder ohne dazwischenliegendem aktiven Medium üblich – der Resonanzraum eines Lasers ist ein extremes Beispiel für Ersteres.
Schlussfolgerung
Unser Experiment zeigt, dass der Strahlungstransport zu den begrenzenden Oberflächen eines IR-aktiven Mediums hauptsächlich aus dem Rückstrahlungsaustausch zwischen den Oberflächen und dem benachbarten Medium besteht. Der Austausch, der in einem Teil des Mediums stattfindet, kann einen geringen Einfluss auf andere Teile haben. Je mehr Teile des Mediums voneinander isoliert sind, desto langsamer ist die Rückkehr zum Gleichgewicht durch Rückstrahlung und Temperaturanpassungen.
In unserem Testfall manifestiert sich ein Anstieg der CO₂-Konzentration von den vorindustriellen Schätzwerten bis zum heutigen Zeitpunkt zunächst in einer Abnahme von 3 W/m² an der TOA und einer Zunahme von 1 W/m² an der Oberfläche. Die Störung durch den CO₂-Anstieg in der gesamten Atmosphäre durchläuft eine Kette von Ereignissen, die darin endet, dass das Energiegleichgewicht am TOA wiederhergestellt wird und ein Temperaturanstieg an der Oberfläche einen Anstieg von 4,2 W/m² zu erfordern scheint [8]. Das ist es aber nicht. Solche scheinbaren Ungereimtheiten treten häufig auf, wenn ein aktives Medium am Transport beteiligt ist [9].
Anmerkungen
1. Eine ernsthafte Frage. In diesem Fall wurden die 3,7 W/m² am TOA mit der Energiedichte verglichen, die erforderlich ist, um einen Anstieg der Oberflächentemperatur von nur 1 K aufrechtzuerhalten, berechnet mit der Stefan-Boltzmann-Gleichung, die 7 W/m² beträgt. Der scheinbare Widerspruch ist leicht zu erkennen.
2. Hayden wird im letzten SEPP-Newsletter zitiert.
3. Dieser Wert von 3,7 W/m² für den „Klimaantrieb“ wird an vielen Stellen zitiert, kann aber durch die Verwendung von MODTRAN mit jedem seiner atmosphärischen Sommermodelle durch Verdoppelung des CO₂ nachgewiesen werden.
4. Hauptsächlich wegen der nicht isotropen Strahlung. Ein Beispiel: Aus einer Höhe von 16 km über der Erdoberfläche werden bei einem Blick auf die untere Hemisphäre 0,28 Steradiane mit einem Hintergrund aus kaltem Raum gefüllt sein, während die restlichen 6,00 Steradiane von der warmen Erdoberfläche eingenommen werden. Dies ist aus dem Bullauge eines Flugzeugs deutlich sichtbar. Aufgrund dieser Veränderung des Hintergrunds wird der durch die Annahme von G= pI berechnete Flusswert zu stark verzerrt sein.
5. Diese lange Liste enthält hauptsächlich Probleme mit der Isotropieannahme in verschiedenen Zusammenhängen. Interessanterweise verwendet der Wrapper nicht p, sondern die Konstante 3,14. Bei keiner dieser Berechnungen gibt es eine Zeitabhängigkeit. MODTRAN-Berechnungen erfolgen augenblicklich, aber die tatsächlichen Veränderungen sind verzögert und brauchen Zeit.
6. Siehe zum Beispiel: Houghton, J.T., 1986, Physics of Atmospheres, 2nd Ed., Cambridge. P. 13. Oder, M. Necati Ozisik, 1973, Radiative Transfer, Wiley-Interscience. S. 320.
7. Man könnte fast sagen, dass die Oberflächentemperatur der Erde einen Großteil ihres eigenen Treibhauseffekts verursacht.
8. Die Rückkehr zum Gleichgewicht kann lange dauern, da sie Veränderungen an der Erdoberfläche wie das Schmelzen von Eis oder die Veränderung der Vegetation mit sich bringen kann.
9. Zu den weiteren offensichtlichen Ungereimtheiten gehört, dass eine steigende CO₂-Konzentration die Erde anscheinend eher abkühlt als erwärmt, insbesondere wenn die IR-aktiven Gase in der Atmosphäre in einer dünnen Schicht in Bodennähe konzentriert sind und die übrige Atmosphäre darüber besonders transparent ist, wie z. B. in der Antarktis oder der winterlichen Arktis oder an der Bodenoberfläche von Hochregionen.
Link: https://wattsupwiththat.com/2023/03/17/the-lwir-puzzle-experiments-with-modtran/
Übersetzt von Christian Freuer für das EIKE