Auswirkungen der Urbanisierung auf die GHCN-Temperaturtrends, Teil III: Verwendung der Bevölkerungsdichte, 1880-2015
Roy W. Spencer, Ph. D., Global Warming Blog
Dies ist der dritte Teil meiner (nicht enden wollenden, wie es scheint) Serie über die Messung der Auswirkungen von städtischen Wärmeinseln (Urban Heat Islands, UHI) auf die Temperaturtrends an der Landoberfläche.
In Teil I [in deutscher Übersetzung hier] und Teil II [in deutscher Übersetzung hier] habe ich den Landsat-basierten „bebauten“ Strukturdatensatz als Stellvertreter für die Verstädterung hervorgehoben. Ich bin sicher, dass wir ihn im Rahmen unseres Zuschusses des Energieministeriums weiter untersuchen werden, um (hauptsächlich) satellitengestützte Methoden und Datensätze zum Testen von Klimamodellen und deren Vorhersagen der globalen Erwärmung zu untersuchen.
Ein Großteil der ursprünglichen Forschung zum UHI-Effekt (z. B. T.R. Oke, 1973 und später) bezog sich auf die Erwärmung im Verhältnis zur Gesamtbevölkerung von Städten. Da die Bevölkerungsdatensätze viel weiter zurückreichen als der Satellitenzeitraum, können sie Informationen über den UHI-Effekt liefern, die bis weit vor 1900 zurückreichen. In den letzten Wochen habe ich einen Umweg über die Landsat-Diagnose menschlicher Siedlungsstrukturen als Näherungswert für die Urbanisierung und die Bevölkerungsdichte gemacht. Dabei musste ich mich mit Problemen im Zusammenhang mit niedrigen Korrelationen und der linearen Regression (insbesondere der Regressionsverdünnung) auseinandersetzen. Ich habe beschlossen, hier nicht darauf einzugehen, weil es etwas zu technisch ist.
Je tiefer ich in dieses Projekt einsteige, desto mehr lerne ich.
Urbanisierungs-Effekte von 1880 bis 2015
Ich habe viele Ergebnisse, die ich zeigen könnte, aber ich denke, ich werde nur eines davon vorstellen, welches von Interesse sein dürfte. Ich verwende Dutzende (in den ersten Jahren) bis Hunderttausende von 2-Stationen-Paaren von Temperaturdifferenzen und PD-Differenzen* und sortiere diese nach der kleinsten bis zur größten durchschnittlichen PD der 2-Stationen. Dann führe ich Regressionen in separaten PD-Intervallen (12 bis 19) durch, um die Veränderung der Temperatur mit der Bevölkerungsdichte (dT/dPD) zu ermitteln. Diese Koeffizienten sind in der Tat Tangenten an die nichtlineare Funktion, die die PD mit dem UHI-Erwärmungseffekt verbindet. Die unten gezeigten Daten stammen aus dem Monat Juni in 20-Jahres-Intervallen von 1880 bis 2015 im Breitenbereich 20N bis 80N.
[*PD = Population Density = Bevölkerungsdichte]
Durch Aufsummieren dieser Regressionskoeffizienten (Integration, in Worten der Infinitesimalrechnung) von Null PD bis zum maximalen PD-Durchschnittswert von zwei Stationen ermittle ich Kurven von PD und UHI-Effekt. Ich habe mir eine ganze Reihe veröffentlichter UHI-Papiere angesehen und kann keinen ähnlichen Ansatz für das UHI-Problem finden.
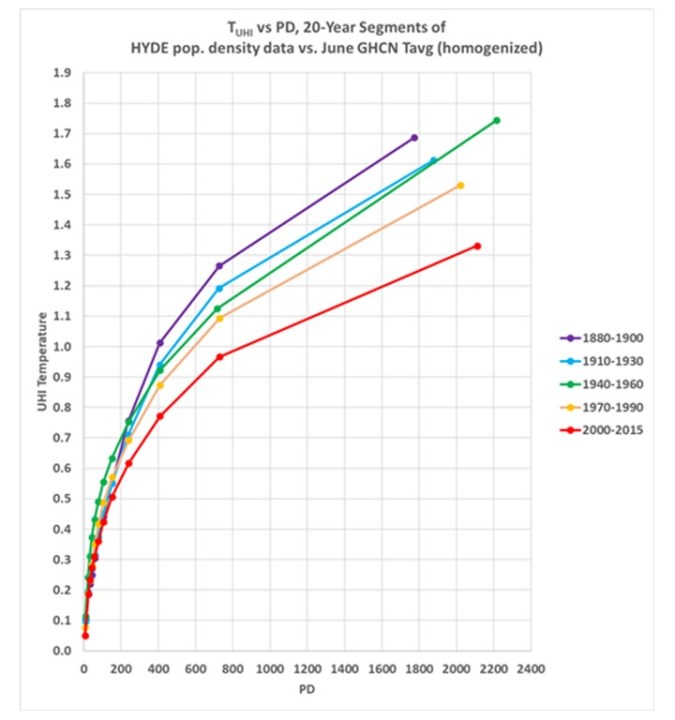
Abb. 1. UHI-Erwärmungskurven als Funktion der 10×10 km großen Bevölkerungsdichte an GHCN-Temperaturmessstationen in fünf verschiedenen 20-Jahres-Zeiträumen von 1800 bis 2015. Die Bevölkerungsdichte (PD, Personen pro km²) und die Temperaturdaten stammen alle 10 Jahre aus dem Monat Juni, und alle Stationspaare in einem Umkreis von 150 km und in einem Höhenabstand von 300 m zueinander wurden berücksichtigt. Die PD-Daten stammen aus dem HYDE 3.2-Datensatz, der auf einem ~10×10 km großen globalen Gitter basiert.
Ich muss zugeben, dass die Ergebnisse in Abb. 1 nicht das sind, was ich erwartet habe. Sie zeigen, dass der gesamte UHI-Effekt im späten 19. Jahrhundert stärker war und sich seitdem etwas abgeschwächt hat. (Zur Erinnerung: Da diese Ergebnisse auf Differenzen zwischen zwei Stationen beruhen, handelt es sich um räumliche Beziehungen, d. h. in den Jahren 1880, 1890 und 1900 ist der Temperaturunterschied zwischen ländlichen und dicht besiedelten Gebieten größer als in späteren Jahrzehnten).
Ich habe keine schlüssige Erklärung dafür, und Vorschläge sind willkommen.
Wären die Ergebnisse umgekehrt, würde ich vermuten, dass dies auf größere Fehler bei den frühen Bevölkerungsschätzungen zurückzuführen ist, da Fehler bei der unabhängigen Variable (PD) die Regressionssteigung (dT/dPD) unter die „wahre“ Beziehung senken (Regressionsverdünnung). Aber genau das Gegenteil ist der Fall. Und es kann nicht an der viel geringeren Anzahl von Stationen in den frühen Perioden liegen, denn das führt nur zu Rauschen in den Regressionskoeffizienten, nicht aber zu systematischer Verzerrung.
Einige Gedanken dazu
Nach der Lektüre der Fachliteratur halte ich dies für einen ziemlich neuen Ansatz, der ein häufiges Problem vermeidet: die übliche Einteilung der Stationen in „ländliche“ und „städtische“ Kategorien. Da die Kurven in Abb. 1 nicht linear sind, wird eine fast ländliche Station bei einem gegebenen Bevölkerungszuwachs eine viel stärkere Erwärmung erfahren als ein sehr städtischer Standort. Daher sind frühere Untersuchungen, die nur geringe Unterschiede in den Temperaturtrends zwischen städtischen und ländlichen Standorten festgestellt haben, nicht wirklich aussagekräftig. Meine Methode umgeht dieses Problem, indem ich Kurven konstruiere, die bei einer Bevölkerungsdichte von Null beginnen (wirklich ländliche Bedingungen).
[Hervorhebungen im Original]
Letztendlich wird all dies zu einer Schätzung darüber führen, wie viel der Erwärmung auf dem Land (z. B. seit 1880) auf den Wärmeinseleffekt in Städten zurückzuführen ist. Wie ich bereits erwähnt habe, glaube ich nicht, dass er groß sein wird. Aber es muss dokumentiert werden.
Übersetzt von Christian Freuer für das EIKE