Verkettete Unsicherheiten

Kip Hansen

[Originaltitel: „Daisy-Chained Uncertainties“ Daisy = Gänseblümchen. – Alle Hervorhebungen in diesem Beitrag im Original]

Wie hoch sind die Wahrscheinlichkeiten? Haben Sie das jemals jemanden fragen hören? Das habe ich sicher. Natürlich fragen sie oft, weil sie keine Ahnung haben, was „Zufall“ ist oder wie man zu einer praktischen Vorstellung davon kommt, „wie hoch die Wahrscheinlichkeit ist“.

Die meisten von uns wissen, dass beim Werfen einer Münze die Wahrscheinlichkeit 50/50 beträgt, dass sie Kopf ergibt. Die Wahrscheinlichkeit, dass sie auf „Zahl“ fällt, ist ebenfalls 50:50. Wir wissen, dass unsere individuelle Wahrscheinlichkeit, von einem Blitz getroffen zu werden, äußerst gering ist. Trotzdem habe ich einen nahen Verwandten, der zweimal vom Blitz getroffen wurde – und beide Male überlebte. Wie groß ist die Wahrscheinlichkeit dafür?!

(Vom Blitz getroffen: Die Schätzungen gehen weit auseinander, aber in den Vereinigten Staaten: „Nach Angaben des National Weather Service hat eine Person eine Wahrscheinlichkeit von 1:15.300, im Laufe ihres Lebens vom Blitz getroffen zu werden, d. h. in einem Zeitraum von 80 Jahren“. Und: „Die Wahrscheinlichkeit, in einem bestimmten Jahr vom Blitz getroffen zu werden, liegt allerdings näher an der 1:1-Million-Marke: 1:1.222.000.“)

Das Thema „Wahrscheinlichkeiten“ ist so umfangreich und komplex, dass der Statistiker William Briggs ein 237-seitiges Buch als Einführung in dieses Thema geschrieben hat.

Regelmäßige Leser werden wissen, dass ich ein eingefleischter Pragmatiker bin – ein praktischer Mensch. Wenn es nicht stimmt, wenn ich mir den Zeh daran stoße, dann ist mir das ziemlich egal. Das bedeutet, dass ich mich eher an berufstätige Ingenieure wende und nicht an Akademiker aller Art, wenn das Thema etwas ist, das ich sehen und anfassen kann.

Mein bevorzugter professioneller Statistiker ist William M. Briggs. Wir haben einen gemeinsamen Hintergrund, der so unterschiedliche Themen wie Kryptologie und Bühnenmagie umfasst. Er veröffentlicht gelegentlich etwas von mir.

Briggs schrieb darüber, was mit der Wahrscheinlichkeit geschieht, wenn mehrere ungewisse Dinge gleichzeitig eintreten müssen. Aber was wir oft in Betracht ziehen müssen, sind verkettete Unsicherheiten.

Was sind daisy-chained Wahrscheinlichkeiten? Etwa so: Wenn meine schwarze Katze, die mit einer Wahrscheinlichkeit von fünfzig zu fünfzig heute Abend nach Hause kommt und dann auf den Hund meines Sohnes trifft, der mit einer Wahrscheinlichkeit von eins zu vier unerwartet bei mir abgegeben wird, damit ich über Nacht auf ihn aufpasse, und wenn man bedenkt, dass der Hund die Katze an einem von fünf Tagen überhaupt nicht verträgt, wie hoch ist dann die Wahrscheinlichkeit, dass es heute Abend zu einem chaotischen Kampf zwischen Hund und Katze in meiner Wohnung kommt?

(Die Wahrscheinlichkeit, dass ein Chaos entsteht, beträgt nur 2,5 %. Ich wäre bereit, diese Wahrscheinlichkeit {und entsprechende Vorsichtsmaßnahmen} in Kauf zu nehmen. Überrascht?)
Natürlich verwendet Briggs kein solches Beispiel eines „Hausherrn“.

Briggs sagt Folgendes:

Hier ein Beispiel aus den jüngsten Nachrichten:

„Phil Trathan: Kaiserpinguine kämpfen sich durch den antarktischen Winter, und sie brauchen das Meereis als stabile Plattform, sie sind also darauf angewiesen, dass das Meer gefriert und eine feste Basis bildet. Und wenn die Temperaturen in der Antarktis steigen, wird das Meereis verschwinden. Und das bedeutet, dass die Kaiserpinguine dann keinen Platz mehr zum Brüten haben werden.“

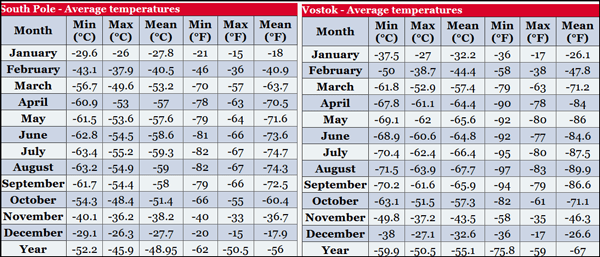
„Falls die Temperaturen in der Antarktis steigen“ bedeutet, dass die Temperaturen hoch genug steigen, um die winterliche Bildung von Meereis zu gefährden:

Die höchste Höchsttemperatur (Monatsdurchschnitt), die in Wostok oder am Südpol gemessen wurde, liegt bei minus 26 Grad Celsius. Antarktis-Experten wissen, dass im Südwinter immer Meereis vorhanden ist, wenn Kaiserpinguine an Land kommen müssen, um Eier zu legen und Küken aufzuziehen. Kaiserpinguine nisten nicht auf dem temporären Meereis, sondern auf dem soliden Festeis oder auf den eisbedeckten Felsen der Antarktis in Küstennähe. Je nach Beschaffenheit der Küstenlinie benötigen sie jedoch oft landgebundenes Meereis, um das Wasser zu verlassen und auf das Land zu gelangen.

Das ist ein Beispiel dafür, wie schlimm die Propaganda werden kann, aber sehen wir uns die Beispiele von Briggs an:

Alle drei Teile der Aussage sind mit ihren eigenen Unsicherheiten behaftet. Wenn wir die Aussage als Ganzes betrachten, dann müssen diese Unsicherheiten mehr oder weniger multipliziert werden, was zu einem Ganzen führt, das weitaus unsicherer ist als jeder einzelne Teil.“

„Diese Münze wird Kopf ergeben, [dann] werde ich mit diesem Würfel eine größere Zahl als eine 3 würfeln und [dann] eine Herz-Acht aus diesem Stapel ziehen.“

Vergessen Sie das nie! Alle Wahrscheinlichkeiten sind bedingte Wahrscheinlichkeiten, d. h. wir müssen Beweise vorlegen, aus denen wir sie berechnen können. Hier habe ich allgemeine Beweismittel ausgewählt. Wir müssen diese für jeden der drei Teile dieses Szenarios annehmen. Für den Münzwurf nehmen wir an: „Hier ist ein Objekt, das, wenn es geworfen wird, nur Kopf oder Zahl zeigen kann“. Daraus leiten wir ab, dass die Wahrscheinlichkeit für Kopf 1/2 ist.

Und so weiter für die anderen. Wir erhalten 1/2 für den Wurf, 1/2 für den Würfelwurf und 1/52 für das Ziehen einer Karte, alles unter der Annahme eines Standardbeweises. Damit das gesamte Szenario wahr ist, müssen wir alle drei Werte erhalten. Die Wahrscheinlichkeiten multiplizieren sich: 1/2 x 1/2 x 1/52 = 1/208, was etwa 0,005 entspricht.“ [Der genauere Wert ist 0,0048076923076923, etwa ½ von 1 % ]

Ich habe diese Beispiele ausgewählt, weil ich denke, dass sie unserem Kaffee-„Klimawandel“-Szenario ähneln, auch wenn die Beweislage schwieriger ist. Gehen wir die einzelnen Teile des Szenarios durch, um zu sehen, wie Aussagen wie diese angegangen werden sollten.

1) Die Bedrohung durch den „Klimawandel“. Darunter verstehe ich, dass die Modelle der Experten, die einen „erheblichen“ „Klimawandel“ vorhersagen, korrekt sind oder dass sich das Klima von selbst verändert, und zwar aus Gründen (zumindest teilweise), die nicht von den Experten in ihren Modellen kodiert wurden. Angesichts der Tatsache, dass Experten seit den 1970er Jahren das Unheil für das Wetter vorhersagen, zuerst, dass es zu kalt sein würde, dann, dass es zu heiß sein würde, dann, dass es einfach zu unterschiedlich sein würde, und dass sie bisher jedes Mal falsch lagen, bin ich nicht allzu scharf auf Expertenmodelle. Aber ich denke auch, dass das Klima der Erde in der Vergangenheit sowohl wärmer als auch kühler, feuchter und trockener, sonniger und bewölkter gewesen ist, also kann es auch wieder so sein.

Es gibt keinen numerischen Wert für die Wahrscheinlichkeit, die sich aus diesen Beweisen ableiten lässt. Sie ist zu vage. Das heißt aber nicht, dass sie nicht nützlich ist. Wenn man nach einer Zahl fragt, liegt sie meiner Meinung nach auf der Grundlage dieser Beweise nicht allzu weit von 50-50 entfernt.

2) Das schlechte Ereignis. Vielleicht würde die Kaffeeproduktion in Afrika bei verändertem Wetter zurückgehen, vielleicht aber auch nicht. Die Aussage, dass sie zurückgehen wird, ist das Ergebnis eines anderen Modells von Experten. Die mit Vorhersagen für die Landwirtschaft gar nicht so gut gefahren sind.

Auch hier lässt sich keine numerische Wahrscheinlichkeit ableiten. Aber ich bin großzügig, also sagen wir wieder 50:50. (In Wirklichkeit glaube ich, dass es weniger ist, aber ich möchte unser Beispiel nicht ändern.)

3) Das Versprechen von „Lösungen“. Die „Lösungen“ der Experten wären hier zweierlei: den Klimawandel zu stoppen und den Rückgang der Kaffeeproduktion abzumildern, wenn sich das Klima in eine Richtung verändert hat, die der Produktion schadet.

Dies ist sogar noch schwieriger, weil in (3) und (1) einige der gleichen Beweise verwendet werden, nämlich die über die Klimamodelle der Experten. Das macht den Multiplikationstrick streng genommen falsch, aber er ist auch nicht allzu abwegig, insbesondere weil die „Lösungen“ der Experten für komplexe Situationen stinken, stanken, gestunken haben. Das Eins zu Fünfzig ist großzügig.

Briggs: Das Endergebnis ist, dass ich mir keine Sorgen über den „Klimawandel“ mache, nicht annähernd so sehr wie über die Annahme von Experten-„Lösungen“, die meiner Einschätzung nach alles nur noch schlimmer machen würden, oder viel schlimmer.

Meine Meinung, die ich mit Briggs (mehr oder weniger) teile ist, dass alle von CliSci vorhergesagten schlechten Auswirkungen diese Art von Gänseblümchenketten-Abhängigkeiten und Wahrscheinlichkeiten aufweisen.

Stellen Sie sich das als „IPCC-Wahrscheinlichkeitsskala“ vor:

Was passiert, wenn nur zwei (2) solcher „Likely“-Aussagen durch Abhängigkeit aneinandergereiht werden.

Ich verwende die beiden unterschiedlichen Punkte innerhalb der Spanne von „Likely“ – 0,70 und 0,85:

Falls „Wahrscheinlich #1: dann falls „Wahrscheinlich #2“ dann Ergebnis (in Wahrscheinlichkeit)

0.70 x 0.85 = 0.595

Bei einer Verkettung von wahrscheinlichen Ereignissen, die voneinander abhängen, wird der Bereich „Wahrscheinlich“ fast erreicht – falls wir aufrunden würden, würden sie es schaffen.

Aber sehen Sie, was passiert, wenn drei wahrscheinliche Ereignisse gleichzeitig eintreten müssen:

0.75 x 0.80 x 0.85 = 0.51

Im Grunde 50-50 im Bereich Ungefähr so wahrscheinlich wie nicht.

0,4 x 0,5 x 0,6 = 0,12

Drei verkettete Ereignisse am unteren Ende von „Ungefähr so wahrscheinlich wie nicht“:

0,35 x 0,35 x 0,35 = 0,043

„Extrem unwahrscheinlich“

Unter dem Strich

1) Alle Wahrscheinlichkeiten für zukünftige Katastrophen von CliSci leiden darunter, dass die Wahrscheinlichkeiten nicht durch Multiplikation der Teilwahrscheinlichkeiten ihrer notwendigen Komponenten berechnet werden. [Die Multiplikation ergibt eine Näherung, die für Pragmatiker gut genug ist.]

2) Man beachte, dass die Wahrscheinlichkeit einer Katastrophe erheblich abnimmt, wenn mehrere Bedingungen („falls dies“) in einer bestimmten zeitlichen Reihenfolge eintreten müssen – wie bei „falls zuerst dies“, „falls als nächstes dies“ dann „eventuell dies“. Die obigen Beispiele betreffen nur die Wahrscheinlichkeit, dass alle Bedingungen eintreten, ohne Rücksicht auf die Reihenfolge. Die Einführung einer neuen Bedingung – die zeitliche Reihenfolge – verringert zwangsläufig die Wahrscheinlichkeit.

3) Für die Klimawissenschaft bedeutet dies, dass wir bei Vorhersagen im Stile des IPCC, die auf Klimamodellen mit sehr großen Streuungen beruhen (z. B. Modelle zur Vorhersage der künftigen globalen Durchschnittstemperatur), bei denen keine Wahrscheinlichkeiten angegeben sind, sondern nur ein breites Intervall möglicher Werte, alle vom IPCC vorhergesagten Ergebnisse überdenken müssen. Und warum? Die Wahrscheinlichkeiten aller vorhergesagten Folgen müssen zumindest grob berechnet werden, indem die Wahrscheinlichkeiten der Bedingungen, die zu diesen Folgen führen, multipliziert werden.

Aufsatz).

Kommentar des Autors hierzu:

Ungewissheit ist heikel, sie ist unsicher, sie kann komplex sein, sie kann kompliziert sein und sie kann chaotisch sein (als Ursache oder Wirkung). Es gibt Leute, die glauben, dass wir die Unsicherheit mit den Zäunen der Statistik sicher einfangen können. Aber diese Idee wird als Schnuller benutzt, um uns davon abzuhalten, uns mit der wirklichen Unsicherheit in der Welt um uns herum auseinanderzusetzen.

Statistische Ansätze sind verlockend – sie geben uns das Gefühl, dass wir alles unter Kontrolle haben, und bringen ein Gefühl der Sicherheit an die Stelle der Unsicherheit. In Anbetracht der Welt, wie sie ist, mag dies für unseren gesunden Menschenverstand notwendig sein.

Ich fürchte, dies ist nur eine weitere Version von etwas, das dem Propter Nomen ähnelt – falls wir es mit „Unsicherheitsbalken“ oder „Standardabweichungen“ oder „Fehlerbalken“ oder, und das gefällt mir, „Konfidenzintervall“ bezeichnen können (was impliziert, dass es sich nicht um die unangenehme Unsicherheit handelt, sondern dass wir uns dessen sicher sind), dann sind wir nicht mehr unsicher. All diese „Unsicherheits“-Ersatzbegriffe sind einfach nur Käfige, in die alle unsicheren Teile unseres Problems eingepfercht zu haben wir hoffen.

Es gibt und wird immer eine gewisse Unsicherheit bei Messungen und Berechnungen geben. Je mehr verschiedene Messungen und Berechnungen beteiligt sind, desto größer wird die Unsicherheit.

Link: https://wattsupwiththat.com/2023/01/17/daisy-chained-uncertainties/

Übersetzt von Christian Freuer für das EIKE