Schwarzschild und die Lösung der Strahlungstransfergleichung – ein physikalischer Hütchentrick?

Vorbemerkung der EIKE Redaktion:

Wie immer bei Artikeln von U.Weber bitten wir evtl. Kommentatoren zunächst die durch Beobachtung gestützte Annahme des Autors zu widerlegen, dass die Sonne immer nur die Tagseite bescheint. Anders ausgedrückt, bitte weisen zunächst nach, dass die vereinfachende Betrachtung, dass die Sonne die ganze Erde Tag und Nacht bestrahlt innerhalb sehr enger Fehlergrenzen (± 0,34 Promille) zulässig ist.

Uli Weber

Die menschengemachte Klimareligion gründet sich auf das Mysterium eines „natürlichen atmosphärischen Treibhauseffektes“ (THE), der angeblich durch den CO₂-Ausstoß aus der technischen Nutzung fossiler Energieträger durch den Menschen noch weiter angeheizt werden soll. Zur wissenschaftlichen Begründung dieses Treibhauseffektes hat man sich der „gemes­senen“ Realität (Near Surface Temperatur = NST) auf unserer Erde über einen globalen 24h-Faktor4-Vollkugel-Durchschnitt der hemisphärischen solaren Einstrahlung auf der Tagseite genähert. Als zwingende rechnerische Kompensation für die dadurch reduzierte theoretische Temperatur wird dann eine terrestrische „Abstrahlungshöhe“ in der Erdatmosphäre behauptet. Diese erfordert wiederum eine sogenannte „atmosphärische Gegenstrahlung“ als Quelle für einen „natürlichen“ Treibhauseffekt. Dieser THE erfüllt den Zweck, die Temperatur von der „Abstrahlungshöhe“, dem tatsächlichen barometrischen Gradienten folgend, am Ende wieder an die „beobachtete“ physikalische Realität an der Oberfläche (NST) anzubinden, wie das im folgenden Beitrag nachgewiesen werden wird. Der THE ist also lediglich die paraphysikalische Kompensation für eine physikalisch fehlerhaft hergeleitete theoretische Faktor4-Temperaturgenese auf unserer Erde.

Hinweis: Der Übersichtlichkeit halber wird hier mit Durchschnittswerten für die Bestrahlungsstärke in [W/m²] analog zur weiter unten verlinkten Vorlage argumentiert. Diese Vorlage ist im Vergleich zu anderen Darstellungen der Strahlungstransfergleichung sehr anschaulich und gut nachvollziehbar. Ich hatte allerdings bereits mehrfach nachgewiesen (beispielsweise hier), dass Durchschnittswerte, angewendet auf das Stefan-Boltzmann-Gesetz, zu physikalisch fehler­haften Ergebnissen führen. Die nachfolgend zitierten Ausschnitte, z.T. mit von mir eingefügten gelben Hervorhebun­gen, stammen aus dem Script „Physik der Atmosphäre“ von Niklaus Kämpfer vom Herbstsemester 2007 am Institute of Applied Physics (IAP) der Uni Bern (letzter Zugriff am 13.12.2022).

Fangen wir also mit der Schwarzschild-Gleichung an:

Ausschnitt 1 von Seite 47 aus der Vorlage „Physik der Atmosphäre“ von Niklaus Kämpfer (2007)

Aus der Schwarzschild-Gleichung leitet sich durch Umformung am Ende dann die sogenannte Strahlungstransfergleichung (STG) her. Diese ist nach dortiger Angabe für alle spektralen Anteile zusammen kaum lösbar:

Ausschnitt 2 von den Seiten 49/50 aus „Physik der Atmosphäre“ von Niklaus Kämpfer (2007)

Vielmehr findet unter der Annahme, dass auf der Erde ein globales thermodynamisches Gleichgewicht (GTE) zwischen Ein- und Abstrahlung (IN=OUT) besteht, eine approximative Abschätzung zur Lösung dieser STG statt. Spannend ist nun, dass als Grundlage für diese Abschätzung einer Lösung im Vakuum plötzlich der umstrittene „Faktor 4“ für die globale 24h-Mittelung der hemisphärischen solaren Einstrahlung auf der Erde auftaucht.

Die Abbildung 3.34 aus dem nachfolgenden Ausschnitt 3 stellt die Situation auf der Erde korrekt dar, die Tagseite der Erde wird von der Sonne bestrahlt und die Abstrahlung erfolgt über die gesamte Erdoberfläche.

Ausschnitt 3 von den Seiten 50/51 aus „Physik der Atmosphäre“ von Niklaus Kämpfer

Trotz dieser korrekten Abbildung 3.34 basiert die vereinfachte Lösung der Strahlungstransfer­gleichung also auf einer globalen Viertelung der spezifischen solaren Einstrahlung auf der Tagseite als Eingangsgröße für die globale Abstrah­lung der Erde. Die globale Faktor4-Mittelung der hemisphärischen solaren Einstrahlung stellt demnach nicht etwa das Ergebnis, sondern eine GRUNDANNAHME für die vereinfachte STG-Lösung dar, weil allein sie die verfügbare spezifische Strahlungsleistung für die Berechnung einer Abstrahlungstemperatur mit dem Stefan-Boltzmann-Gesetz vorgibt. Dieser globale Tag=Nacht-Faktor 4 ist in allen mir bekannten Lösungs­ansätzen für die STG als Anfangsbe­dingung enthalten und erfordert regelmäßig einen sogenannten „natürlichen“ THE. Denn die solchermaßen für jede individuelle Ortslage auf der Erdoberfläche mit dem 24h-Faktor4 über die Nachtseite mit (0W/m²) gemittelte Nettostrahlungsleistung beträgt dann eben nur noch durchschnittlich 235 W/m². Daraus ergibt sich dann ein S-B-Temperatur­äquivalent von lediglich T_eq=T_s=255 Kelvin (=-18°C) für jeden Ort auf der Erd­oberfläche. Dabei wird aber die terrestrische Temperaturgenese auf der Tageseite unserer Erde übersprun­gen, durch die erst eine Richtungsumkehr des Poynting-Vektors zwischen Ein- und Abstrahlung möglich wird, wie in 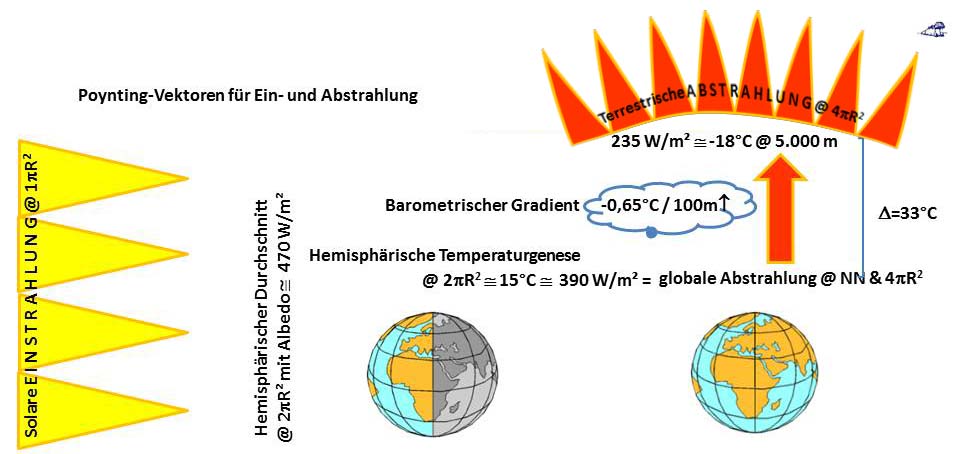Abbildung 1 gezeigt wird. Denn ein Vektor ändert nun einmal nicht grundlos seine Richtung:

Abbildung 1: Terrestrische Temperaturgenese mit der solaren Einstrahlung (@1PIR²=Kreisfläche mit Erdradius), dem hemisphärischen Durchschnitt (@2PIR²=Halbkugel)* und der durchschnittlichen Abstrahlung* (@4PIR²=Kugelfläche), sowie den einander gegenläufigen Poynting-Vektoren

*) Es sei ausdrücklich auf meinen Hinweis zu Durchschnittswerten am Anfang dieses Textes verwiesen

In meinem hemisphärischen S-B-Modell wirkt dagegen die auf der Tagseite in Atmosphäre und Ozeanen gespeicherte Wärme durch die Erddrehung auf der Nachtseite weiter. Schon Wiener unterscheidet übrigens in seiner Arbeit „Ueber die Stärke der Bestrahlung der Erde durch die Sonne in den verschiedenen Breiten und Jahreszeiten“ (1879, Meteorologische Zeitschrift, 113-130) zwischen „Intensität“ und „Strahlenmenge“, Zitat von Seite 115:

„Aus der Formal (2) ergibt sich dw:dt als die Intensität der Sonnenbestrahlung, d. i. als die in der (durch Bogen ausgedrückten) Zeiteinheit auftreffende Strahlenmenge; ebenso ist bei senkrecht auffallenden Strahlen W:2 die Intensität der Bestrahlung;…“

Im „just-in-time“-Gesetz von Stefan und Boltzmann „kann es nur einen geben“, und das ist nun einmal die „Strahlstärke“. Denn man kann der Tagseite in einem Quotienten aus [Arbeit/Zeit] nicht einfach einen Teil der solaren Strahlstärke wegnehmen und willkürlich der Nachtseite zuschlagen. Die korrekte Lösung von Gerlich (1995) für ein solches Faktor4-Modell beträgt daher lediglich 144 Kelvin. Meine diesbezügliche Korrektur für die Taghalbkugel allein kommt damit auf 288 Kelvin, was der global gemittelten Tag&Nacht-Sommer&Winter-Land&Meer-NordHK&SüdHK-NST entspricht.

Bei der fehlerhaft vereinfachten Lösung der STG in Ausschnitt 3 erhält man nun eine „Faktor4-Gleichgewichts-Temperatur“ T_eq=255 Kelvin für die gesamte Erdoberfläche im Vakuum. Dort heißt es dann, diese Temperatur habe angeblich „nicht viel mit der Oberflächen­temperatur [NST] zu tun“ (WIDERSPRUCH 1), sondern soll als Vakuum-Lösung jetzt plötzlich eine atmosphärische Abstrahlungs­tempera­tur in 5.000 Metern Höhe darstellen, was zu einem weiteren WIDERSPRUCH 2 führt. Diese „Abstrahlungs­temperatur“ ergibt sich nämlich auch „GANZ ZWANGLOS“, und zwar ohne irgendeinen THE, ganz allein aus der „gemessenen globalen Durchschnitts­tem­peratur“ (NST) von 15°C über den barometrischen Gradienten von [-6,5K/1.000 m] mit einer Temperatur von [-18°C] in 5.000 Metern Höhe (Siehe Abbildung 1). Um nun diesen Sprung vom Vakuum an der Oberfläche auf die sogenannte „Abstrahlungshöhe“ in der Atmosphäre zu verschleiern, wird eine sogenannte „atmosphärische Gegenstrahlung“ eingeführt. Dazu wird das besagte globale thermodynamische Gleichgewicht (GTE) für die nachstehenden ein- und ausgehenden Strahlungsflüsse eingefordert, weil es sonst begreiflicherweise zu einer ständigen Erwärmung oder Abkühlung der Erde kommen würde:

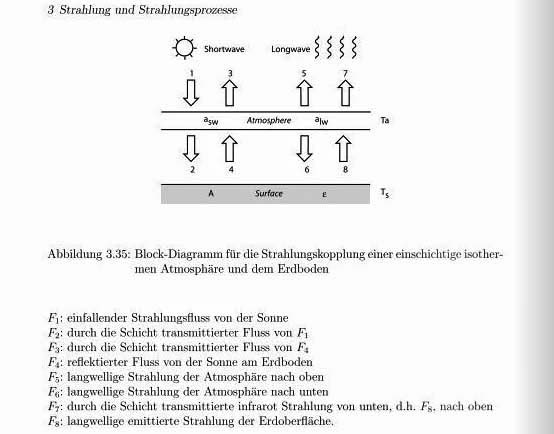Ausschnitt 4 von Seite 52 aus der Vorlage „Physik der Atmosphäre“ von Niklaus Kämpfer (2007)

Es handelt sich bei den hier dargestellten Strahlungsflüssen um eine vorgegebene Modellvorstellung, die, wie bereits ausgeführt worden ist, von vorn herein eine sogenannte „Gegenstrahlung“ einschließt, aber nicht beweist. Daraus ergibt sich in der Vorlage nun ein Gleichungssys­tem, das nach der Oberflächentemperatur und der Temperatur der Atmosphäre aufgelöst wird:

Ausschnitt 5 von Seite 53 aus der Vorlage „Physik der Atmosphäre“ von Niklaus Kämpfer (2007)

Randnotiz: Im Text wird dann die Oberflächentemperatur T_s unter verschiedenen Eckwerten diskutiert. Wenn wir nun aber die Temperatur der Atmosphäre T_a aus Gleichung (3.99) berechnen, dann erhalten wir eine Temperatur von 2,8 Kelvin. Da stimmt also schon einmal irgend­etwas mit der Formel nicht. Wenn wir dort aber [S/4] tentativ aus Formel (3.100) durch [S_c/4SIGMA] ersetzen, werden es plötzlich 257 Kelvin, was dem Wert für T_eq von 255 Kelvin sehr nahe kommt.

Mit der dort vorgegebenen langwelligen [a_l=0,8] und kurzwelligen [a_s=0,2] Absorption ergibt sich aus Formel (3.98) dann ein Wert von T_s=288 Kelvin (in der Vorlage sind es 286K) für die Erdoberfläche.

Worin könnte nun ein physikalischer Hütchentrick im Lösungsverlauf der STG bestehen?

Nun, in der oben verlinkten Vorlage hat man als Eingangsvoraussetzung für eine approximative Lösung der STG die hemisphärisch einfallende solare Strahlungsleistung in unzulässiger Weise auf ein globales 24h-Faktor4-Mittel beschränkt. Folglich beträgt dann die kurzwellige solare Nettoeinstrahlung auf der Erdoberfläche im Vakuum auch nur noch 235 W/m² und das entsprechende S-B-Temperaturäquivalent T_eq=T_s=255 Kelvin. Die langwellige terrestrischen Abstrahlung aus der „gemessenen“ globalen Durchschnittstemperatur von [15°C=288 Kelvin] erfordert damit den tatsächlichen barometrischen Gradienten von [-6,5°C/1.000m], um nach Aus­schnitt 3 (Text unten) in 5.000 Metern „Abstrahlungshöhe“ schließlich ebenfalls diese sogenannte „Abstrahlungs­temperatur“ von 255 Kelvin oder [-18°C] zu erzeugen, wie das auch in Abbildung 1 dargestellt ist. Zwischen der Faktor4-Berech­nung und der physikalischen Realität klafft also der Widerspruch 1 von (255 Kelvin = 288 Kelvin). Dieser Widerspruch von 33 Kelvin wird nach dem Faktor4-THE-Modell aufgelöst, indem 80% der langwelligen terrestrischen Abstrahlung aus der „gemessenen“ NST von der Atmos­phäre absorbiert werden sollen, also 80% von 390 W/m² (= 310 W/m²), und als sogenannte „Gegenstrahlung“ jeweils zur Hälfte auf die Erdoberfläche und in den Weltraum gerichtet sind.

Geheilt wird der Widerspruch 1 also durch die paraphysikalische Zustrahlung von weiteren 155 W/m² als sogenannter THE aus der kälteren Atmosphäre auf die wärmere Erdoberfläche unter Umgehung des 2. HS der Thermodynamik. Auf der vorgeblichen Abstrahlungshöhe von 5.000 Metern sollen folglich [(390-310) W/m² + 155 W/m² = 235 W/m²] in den Weltraum abgestrahlt werden und damit das Kriterium [IN=OUT] für den Strahlungshaushalt unserer Erde erfüllen. Aber diese, in einem frag­würdigen (Huhn&Ei)-Kreisprozess konstruierte, tertiäre „Gegenstrahlung“ von 310 W/m² erfordert nun für ihre Existenz ganz genau diejenige sekundäre Oberflächenabstrahlung von 390 [W/m²], die sie mit einer atmosphärischen Zustrahlung von 155 [W/m²] ja erst selbst erzeugt haben soll.

Rein mathematisch ist dieses THE-Modell schlüssig: Wir haben zwei fest vorgegebene Eckwerte (F_s=390W/m²) aus der sogenannten „gemessenen globalen Durchschnittstemperatur“ (NST) von [15°C] und (F_a=235W/m²) aus einem fehlerhaft global berechneten Stefan-Boltzmann-Temperaturäquivalent von [-18°C]. Die abhängigen Unbekannten in diesem THE-Modell sind dann die „Gegenstrahlung“ (F_g) und die Abstrahlung der Oberfläche im atmosphärischen Fenster (F_f). Rein mathematisch lassen sich diese beiden Zahlenwerte daher durch zwei Gleichungen ([1] und [2]) mit den zwei Unbekannten (F_g und F_f) herleiten:

[1] F_s [W/m²] – F_g/2 [W/m²] = F_f [W/m²] + F_g/2 [W/m²]
In Worten: Die langwellige Abstrahlung von der Erdoberfläche F_s minus dem halben Betrag der Gegenstrahlung F_g/2 ist gleich der langwelligen Abstrahlung im atmosphärischen Fenster F_f plus der halben Gegenstrahlung F_g/2.

[2] F_f [W/m²] + F_g/2 [W/m²] = F_a [W/m²]
In Worten: Die langwellige Abstrahlung im atmosphärischen Fenster F_f plus dem halben Betrag der Gegenstrahlung F_g/2 ist gleich der langwelligen Abstrahlung der Atmosphäre F_a auf der sogenannten „Abstrahlungshöhe“ von 5.000 Metern.

mit F_s = 390 [W/m²] = IR-Abstrahlung der Erdoberfläche bei [15°C]

F_a = 235 [W/m²] = Abstrahlung der Atmosphäre in 5 [km] Höhe bei [-18°C]

F_g = „atmosphärische Gegenstrahlung“

F_f = Abstrahlung der Oberfläche im atmosphärischen Fenster

[2‘] Gleichung [2] wird als Gleichung [2‘] nach F_f aufgelöst:
(F_f [W/m²] = F_a [W/m²] – F_g/2 [W/m²]) und in Gleichung [1] eingesetzt:

[3] 390 [W/m²] – F_g/2 [W/m²] = 235 [W/m²] – F_g/2 [W/m²] + F_g/2 [W/m²]

[4] 390 [W/m²] – F_g/2 [W/m²] = 235 [W/m²]

[5] F_g/2 = 390 [W/m²] – 235 [W/m²] = 155 [W/m²]

[6] F_g = 310 [W/m²] als sogenannte „atmosphärische Gegenstrahlung”

[7] Aus Gleichung [2‘] ergibt sich somit F_f [W/m²] = 80 [W/m²] für die direkte IR-Abstrahlung von der Erdoberfläche im atmosphärischen Fenster.

[8] Und für a_l = F_g/F_s ergibt sich dann: a_l = 310/390 = 0,79487179

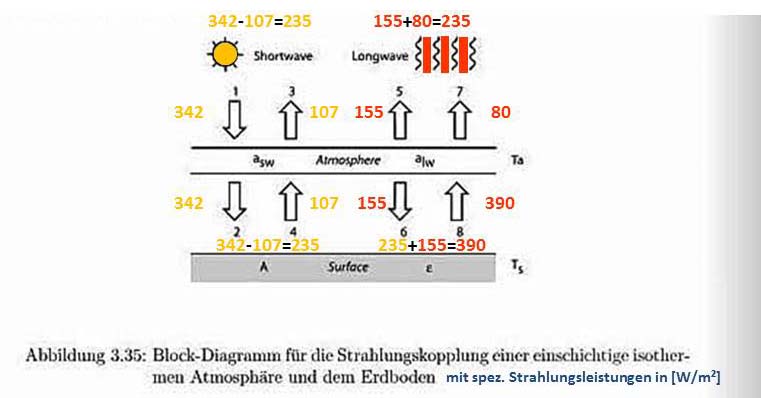Damit ergeben sich für das Faktor4-Tag=Nacht-Modell in Blockdiagramm 3.35 aus Ausschnitt 4 am Ende folgende spezifischen Strahlungsleistungen:

Abbildung 2: Das Blockdiagramm 3.35 aus Ausschnitt 4 (Kämpfer 2007) mit den Richtungen der spezifischen Strahlungsleistungen (F1) bis (F8) nach dortiger Beschreibung und den Ergebnissen aus meinen Gleichungen [1] bis [8]

Mit den Berechnungen aus den Gleichungen [1] bis [8] kann man also die spezifischen Strahlungsleistungen im Blockdiagramm 3.35 aus Ausschnitt 4 mathematisch quantifizieren. Auffällig ist aber der physikalische Zirkelschluss rechts unten zwischen der Oberfläche und der Atmosphäre. Die Abstrahlung von 390 [W/m²] erfordert nämlich die Zustrahlung der sogenannten „atmosphärischen Gegenstrahlung“ von 155 [W/m²], um zusammen mit der solaren Faktor4-netto-Einstrahlung von 235 [W/m²] diese „Gegenstrahlung“ überhaupt erst zu erzeugen.

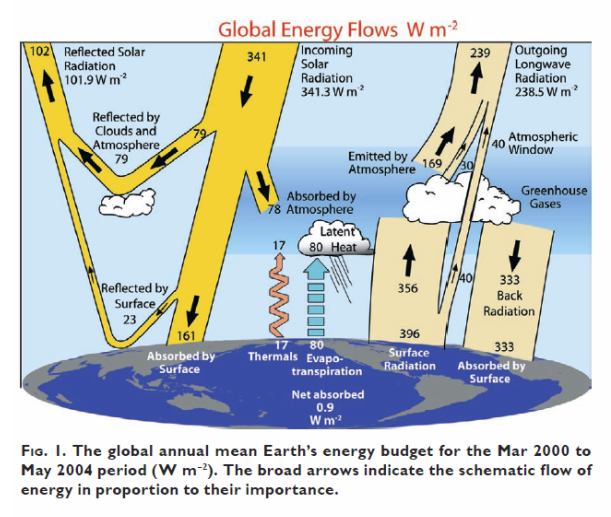Abbildung 3: Fig. 1 aus K. E. Trenberth, J. T. Fasullo, J. Kiehl, “Earth’s global energy budget”, Bulletin of the American Meteorological Society, 90, 311–323, http://dx.doi.org/10.1175/2008BAMS2634.1

Weiterhin ist der Absorptionskoeffizient [a_l] aus Gleichung 3.99 für die langwellige terrestrische Abstrahlung ganz offensichtlich kein nachprüfbarer Meßwert, sondern ergibt sich rein mathematisch über die vorgegebene Modellvorstellung sowie die Eckwerte F_s und F_a und erfordert daher eine physikalische Validierung. Nehmen wir jetzt also einmal die vorstehend berechneten Werte für die Gegenstrahlung F_g (2*155 [W/m²]) und die terrestrische Abstrahlung im sogenannten atmosphärischen Fenster von F_f =80 [W/m²] und vergleichen sie mit dem Diagramm von Trenberth, Fasullo und Kiehl (2009):

 

In der Grafik von Trenberth et al. (2009) verläuft die atmosphärische Gegenstrahlung mit 333 [W/m²] vollständig in Richtung Erdoberfläche, während sich die 310 [W/m²] aus der Näherungslösung für die STG als vektorielles Nullsummenspiel jeweils zur Hälfte in einen aufsteigenden (155W/m²) und einen absteigenden (155W/m²) Energietransport aufteilen. Es differieren also nicht nur die absoluten Werte, vielmehr unterscheiden sich beide auch noch in ihrer vektoriellen Wirkung. Diese Diskrepanz in Betrag und Richtung der sogenannten atmosphärischen Gegenstrahlung stellt einen physikali­schen WIDERSPRUCH 3 in der Theorie für den sogenannten „natürlichen atmosphärischen Treib­hauseffekt“ dar. Weiterhin wird bei Trenberth et al. (2009), wie übrigens auch bei Kiehl und Trenberth (1997)=KT97, die terrestrische Abstrahlung im atmosphärischen Fenster mit 40 [W/m²] bezif­fert, während sich aus der vereinfachten STG-Lösung ein Wert von 80 [W/m²] ergibt. Die implizite Aussage (40 [W/m²] = 80 [W/m²]) für die langwellige Abstrahlung der Oberfläche im atmosphä­rischen Fenster führt damit zu einem physikalischen WIDERSPRUCH 4. Die vereinfachte STG-Lösung kann den sogenannten „natürlichen atmosphärischen Treibhauseffekt“ aus sich heraus also gar nicht beweisen. Die fehlerhaft vereinfachte STG-Lösung über eine widersinnige und unbewiesene Faktor4-Tag=Nacht-Berechnung zieht vielmehr zwangsläufig die beschriebenen Kompensationsmaß­nahmen einer „atmosphärischen Abstrahlungshöhe“, einer „Gegenstrahlung“ und damit eines vorgeblichen THE nach sich, um am Ende wieder an die „gemessene“ Realität einer NST anschließen zu können:

• Der physikalisch widersinnige „Faktor 4“ ist eine unbewiesene GRUNDANNAHME für die vereinfachte Lösung der Strahlungstransfer­gleichung.
• WIDERSPRUCH 1: (255 Kelvin = 288 Kelvin) für die Oberflächentemperatur der Erde
• WIDERSPRUCH 2: Die Faktor4-Rechnung im Vakuum hat ihr Ergebnis in der Atmosphäre.
• Die sogenannte „Abstrahlungstemperatur“ in einer Höhe von 5.000 Metern ergibt sich „GANZ ZWANGLOS“ über den barometrischen Gradienten aus der „gemessenen“ NST (Abbildung 1).
• WIDERSPRUCH 3: (333 [W/m²] = 2 * 155 [W/m²]) für die atmosphärische Gegenstrahlung
• WIDERSPRUCH 4: (40 [W/m²] = 80 [W/m²]) für die Abstrahlung im atmosphärischen Fenster

Fazit: Die vereinfachte STG-Lösung ist von Beginn an mit dem Tag=Nacht-Faktor4 kontaminiert. Ausgehend von dieser Faktor4-Mittelung über die „Abstrahlungshöhe“ und die „Gegenstrahlung“ bis hin zum sogenannten THE als Angleich an die „gemessene“ NST schließt sich ein paranormaler Kreis­prozess à la Chuck Norris, der bekanntermaßen in einem Blockhaus geboren wurde, das er selbst erbaut hat. Was liegt daher näher, als unserer Erde eine „natürliche“ Durchschnittstemperatur von 15°C zuzugestehen, die einem S-B-Strahlungsäquivalent von 390 [W/m²] entspricht. Auf der Tagseite wird diese Temperatur durch die hemisphärische Sonneneinstrah­lung erzeugt, während sie auf der Nachtseite von den globalen Wärmespeichern (Atmosphäre und Ozeane) gestützt wird. Die globale Abstrahlung folgt dann dem natürlichen barometrischen Gradienten auf eine Abstrahlungshöhe von 5.000 Meter mit einer spezifischen Abstrahlungsleistung von 235 [W/m²].

Die Anhänger der Faktor4-Mittelung haben somit aufs falsche Pferd gesetzt, nämlich auf einen globalen solaren 24h-Tag=Nacht-Strahlungsdurchschnitt für die terrestrische Temperaturgenese anstatt auf dessen maximale hemisphärische Intensität. Nur mein hemisphärisches Stefan-Boltzmann-Modell (Prinzip in Abbildung 1) kann die sogenannte „gemessene globale Durchschnittstemperatur“ widerspruchsfrei und ohne die paraphysikalische Hilfskonstruktion eines „natürlichen atmosphärischen Treibhauseffektes“ allein aus der hemisphärischen solaren Einstrahlung heraus erklären (Nachweis in diesem Beitrag auf EIKE sowie in diesem Buch).