Verzerrungen bei Klima-Fingerabdruck-Verfahren
Ross McKitrick, Climate Etc.
● Optimal Fingerprinting ist ein statistisches Verfahren, das die Wirkung von Treibhausgasen (THG) auf das Klima in Form eines Regressionskoeffizienten schätzt.
● Je größer der mit den Treibhausgasen assoziierte Koeffizient ist, desto größer ist die angenommene Wirkung auf das Klimasystem.
● Im Jahr 2003 veröffentlichten Myles Allen und Simon Tett einen einflussreichen Artikel in Climate Dynamics, in dem sie die Verwendung eines Verfahres namens Total Least Squares in der optimalen Fingerprinting-Regression empfahlen, um eine potenzielle Verzerrung nach unten zu korrigieren, die mit Ordinary Least Squares veerbunden ist.
● Das Problem ist, dass TLS in den meisten Fällen die abwärts gerichtete Verzerrung von OLS durch eine aufwärts gerichtete Verzerrung ersetzt, die genauso groß oder größer sein kann.
● Unter bestimmten Bedingungen liefert TLS unverzerrte Schätzungen, aber man kann nicht testen, ob sie zutreffen.
● Ökonometriker verwenden TLS nie, weil ein anderes Verfahren (Instrumentalvariablen) eine bessere Lösung für das Problem darstellt.
Introduction
Das Verfahren des „optimalen Fingerabdrucks“ funktioniert durch Regression eines Vektors von Klimabeobachtungen auf eine Reihe von Klimamodell-generierten Analoga (so genannte „Signale“), die selektiv den Treibhausgasantrieb ein- oder ausschließen. Nach der dem Verfahren zugrunde liegenden Theorie zeigt der mit dem Treibhausgas-Signal verbundene Koeffizient das Ausmaß der Wirkung der Treibhausgase auf das reale Klima an. Wenn der Koeffizient größer als Null ist, wird das Signal „entdeckt“. Je größer der Wert des Koeffizienten ist, desto größer ist die implizierte Wirkung auf das reale Klima.
Das wegweisende Verfahren des optimalen Fingerabdrucks wurde 1999 in einem Climate Dynamics-Papier von Myles Allen und Simon Tett vorgestellt. Mit einigen Modifikationen wird sie seither von Klimawissenschaftlern häufig verwendet. Letztes Jahr habe ich in Climate Dynamics einen Artikel veröffentlicht, der zeigt, dass die Grundlage für die Annahme fehlerhaft ist, dass das Verfahren unvoreingenommene und aussagekräftige Ergebnisse liefert. Diese Website enthält Links zu meinem Aufsatz sowie zu dem von mir kritisierten Aufsatz von Allen und Tett (1999), eine nichttechnische Zusammenfassung meiner Argumente, Myles Allens Antwort und meine Antwort sowie einen Kommentar von Richard Tol.
Eines der Argumente, die Allen in seiner Antwort vorbrachte war, dass das Thema jetzt hinfällig sei, weil das von ihm mitverfasste Verfahren durch neuere Verfahren ersetzt worden sei (Hervorhebung hinzugefügt):
„Der ursprüngliche Rahmen von AT99 wurde durch den Total Least Squares-Ansatz von Allen und Stott (2003) abgelöst, und dieser wiederum wurde weitgehend durch die regularisierte Regression oder die Wahrscheinlichkeit maximierende Ansätze ersetzt, die völlig unabhängig voneinander entwickelt wurden. Um es etwas salopp auszudrücken: Es ist ein bisschen so, als würde jemand vorschlagen, dass wir alle mit dem Autofahren aufhören sollten, weil ein neues Problem mit dem Ford Modell T entdeckt wurde.“
Ha ha, Model T Ford; wir fahren jetzt alle Teslas, auch bekannt als Total Least Squares. Aber hat irgendein Klimawissenschaftler in den 20 Jahren, in denen TLS verwendet wurde, überprüft, ob das Problem tatsächlich gelöst wird? Ein paar Statistiker haben sich im Laufe der Jahre damit befasst und erhebliche Zweifel an TLS geäußert. Aber sobald es von den Klimatologen angenommen wurde, war es das; mit wenigen Ausnahmen stellte niemand Fragen.
Ich habe gerade einen neuen Artikel in Climate Dynamics veröffentlicht, in dem ich die Verwendung von TLS in Fingerprinting-Anwendungen kritisiere. TLS sollte eine mögliche Verzerrung der OLS-Koeffizientenschätzungen nach unten korrigieren, die den Einfluss von Treibhausgasen auf das Klima unterbewerten könnte. Es gibt zwar das berechtigte Argument, dass OLS nach unten verzerrt sein kann, aber das Problem ist, dass TLS bei typischer Anwendung nach oben verzerrt ist, mit anderen Worten, dass es den Einfluss von Treibhausgasen überbewertet. Es gibt einen Sonderfall, in dem TLS unverzerrte Ergebnisse liefert, aber ein Benutzer kann nicht wissen, ob ein Datensatz diese Bedingungen erfüllt. Darüber hinaus ist TLS speziell für die Prüfung der Nullhypothese bei der Signalerkennung ungeeignet, und seine Ergebnisse sollten mit OLS bestätigt werden.
Das Fehler-in-Variablen-Problem und die Schwäche von TLS
OLS-Modelle gehen davon aus, dass die erklärenden Variablen in einer Regression genau gemessen werden, so dass die „Fehler“, die die abhängige Variable von der Regressionslinie trennen, ausschließlich auf Zufälligkeiten in den abhängigen Variablen zurückzuführen sind. Wenn die erklärenden Variablen ebenfalls Zufälligkeiten enthalten, zum Beispiel aufgrund von Messfehlern, führt OLS in der Regel zu verzerrten Steigungsschätzern. In einem einfachen Modell mit einer erklärenden (x) und einer abhängigen (y) Variable ist die Verzerrung nach unten gerichtet, was als „Abschwächungsverzerrung“ bezeichnet wird. David Giles hat hier eine schöne Erklärung des Problems, und Sie können auch in Ökonometrie-Texten wie Wooldridge oder Davidson und MacKinnon nachschlagen.
Das Messproblem wird als Fehler in Variablen oder EIV bezeichnet. Da Klimamodelle verrauschte oder unsichere Schätzungen der wahren Klima-„Signale“ liefern, schlugen Allen und Stott (2003) das TLS-Verfahren als Abhilfe vor. Dies ist nicht die Art und Weise, wie die Ökonometrie mit diesem Problem umgeht. In allen Ökonometrie-Lehrbüchern, die mir bekannt sind, wird für EIV die Schätzung von Instrumentalvariablen empfohlen, die nachweislich unverzerrte und konsistente Koeffizientenschätzungen liefert. Ich habe noch nie gesehen, dass TLS in irgendeinem Ökonometrie-Lehrbuch behandelt wurde, niemals. Ich habe auch noch nie gesehen, dass es in den Wirtschaftswissenschaften oder irgendwo anders außerhalb der Klimatologie verwendet wird, außer in der kleinen Literatur, die sich mit den Eigenschaften von TLS-Schätzern befasst, vor allem in einem Buch von Wayne Fuller aus dem Jahr 1987, einem Artikel von Leon Gleser in den Annals of Statistics aus dem Jahr 1981 und einem Artikel von RJ Carroll und David Ruppert in The American Statistician aus dem Jahr 1996.
Sowohl Fuller als auch Gleser erörtern die Schwierigkeit zu beweisen, dass TLS (oder orthogonale Regression, wie sie üblicherweise genannt wird) unverzerrte und konsistente Schätzungen liefert. Wie Carroll und Ruppert erläutern, besteht das Problem darin, dass das Verfahren die Schätzung von mehr Parametern erfordert, als in den Daten „ausreichende Statistiken“ vorhanden sind: mit anderen Worten, mehr Parameter, als die Daten identifizieren können. Die Umsetzung von TLS erfordert daher die willkürliche Wahl des Wertes eines der Parameter. Sowohl y als auch x haben Fehlerterme mit Varianzen, die geschätzt werden müssen, und in der Praxis wird angenommen, dass sie gleich sind, so dass nur einer geschätzt werden muss. Wenn sie gleich sind, zeigt Gleser, dass die TLS-Schätzung konsistent ist (was bedeutet, dass jede Verzerrung gegen Null geht, wenn die Stichprobe ins Unendliche geht). Ist dies nicht der Fall, kann die Konsistenz nicht garantiert werden. Für die Anwendung der Signaldetektion bedeutet dies, dass TLS keine unverzerrten Steigungskoeffizienten liefern kann, es sei denn, die modellerzeugten Signale enthalten Zufallsfehler mit genau der gleichen Varianz wie die Zufallsfehler im beobachteten Klima (oder sie können so umskaliert werden, dass sie gleich sind).
Carroll und Ruppert weisen auch darauf hin, dass TLS von der Annahme abhängt, dass das Regressionsmodell selbst korrekt spezifiziert ist, mit anderen Worten, das Regressionsmodell umfasst alles, was die Variationen der abhängigen Variable erklärt. OLS geht ebenfalls von dieser Annahme aus, ist aber robuster gegenüber Modellfehlern. Wenn das Modell eine oder mehrere Variablen auslässt, die jedoch nicht mit den eingeschlossenen Variablen korreliert sind, werden die OLS-Koeffizienten nicht verzerrt, wenn jedoch eine der ausgelassenen Variablen mit der eingeschlossenen Variable korreliert ist, wird OLS je nach Vorzeichen der Korrelation nach oben oder unten verzerrt. Bei TLS tritt die Verzerrung in beiden Fällen auf, unabhängig davon, ob die ausgelassene Variable mit den eingeschlossenen Variablen korreliert ist oder nicht, aber die Verzerrung ist immer nach oben gerichtet. Sofern Sie nicht zufällig ein Regressionsmodell haben, das die abhängige Variable vollständig erklärt, so dass bei Abwesenheit von Zufallsrauschen jede Beobachtung genau auf der Regressionslinie liegen würde, sollte die Standardannahme sein, dass TLS die Parameterwerte überschätzt.
TLS kann also im Prinzip unverzerrte Signalerkennungskoeffizienten liefern, aber nur, wenn das Klimamodell, das die Signale erzeugt, alles enthält, was das beobachtete Klima erklärt, und den Signalen zufälliges Rauschen hinzufügt, das genau die gleiche Varianz hat wie die Zufälligkeit im beobachteten Klima. Wenn diese Behauptungen wahr wären, bräuchten wir natürlich gar nicht erst Regressionen zur Signalerkennung durchzuführen. Wenn wir wissen wollten, wie Treibhausgase das Klima beeinflussen, könnten wir einfach in das Modell schauen. Signal-Entdeckungs-Regressionen sind durch die Tatsache motiviert, dass Klimamodelle weder perfekt noch vollständig sind, doch die Behauptung, dass die Ergebnisse unverzerrt sind, setzt voraus, dass sie beides sind.
Vergleich von TLS und OLS in der Praxis
Um zu untersuchen, wie sich diese Probleme auf die Regressionen zur Signalerkennung auswirken, habe ich die Regressionen wie folgt simuliert. Stellen Sie sich eine Stichprobe von Temperaturtrends (y) aus einer Stichprobe von 200 Orten vor, die sich vom Nordpol bis zum Südpol erstreckt. Ich habe zwei unkorrelierte erklärende Variablen X1 und X2 konstruiert. X1 kann man sich als 200 simulierte Trends (oder „Signale“) für diese Orte vorstellen, die aus einem Modell stammen, das mit anthropogenen Treibhausgasen forciert wurde, und X2 stammt aus einem Modell, das nur natürliche Einflüsse berücksichtigt. Dann habe ich den X’s etwas zufälliges Rauschen hinzugefügt, was die Zufallsvariablen W1 und W2 ergibt. Da jedes Regressionsmodell potenziell mindestens eine relevante erklärende Variable auslässt, habe ich außerdem zwei zusätzliche Variablen Q1 und Q2 erstellt. Q1 ist einfach ein unkorrelierter Satz von Zufallszahlen. Q2 ist ein Satz von Zufallszahlen, die teilweise mit X1 korreliert sind.
Dann habe ich 9 Versionen der abhängigen Variable y erstellt:
Y1 = bX1 + X2/2 + v, dabei ist b gleichgesetzt mit 0,0; 0,5 oder 1,0; und v ist weißes Rauschen
YQ1 = bX1 + X2/2 + Q1 + v
und
YQ2 = bX1 + X2/2 + Q2 + v;
und in den beiden letztgenannten Fällen durfte b wiederum 0,0, 0,5 oder 1,0 sein.
Ich habe jede Version von y auf W1 und W2 regressiert:
Y1 = b1 W1 + b2 W2 + e;
YQ1 = b1 W1 + b2 W2 + e
und
YQ2 = b1 W1 + b2 W2 + e.
Jedes Mal schätzte ich die Koeffizienten b1 und b2 sowohl mit OLS als auch mit TLS. Konstruktionsbedingt sollte b2 immer gleich 0,5 sein, und ich habe mich nicht darauf konzentriert. Stattdessen habe ich mich auf b1 konzentriert, das je nach Simulation 0,0, 0,5 oder 1,0 betragen sollte.
Wichtig ist, dass ein Forscher nicht weiß, welche abhängige Variable er verwendet hat. Wenn wir annehmen, dass es sich um Y1 handelt, gehen wir davon aus, dass das Regressionsmodell korrekt spezifiziert ist, das einzige Problem ist, dass W1 eine verrauschte Version von X1 ist. Wenn wir YQ1 verwenden, bedeutet das anzunehmen, dass das Regressionsmodell eine unkorrelierte erklärende Variable auslässt, und wenn wir annehmen, dass wir YQ2 verwenden, bedeutet das, dass das Regressionsmodell eine korrelierte erklärende Variable auslässt. Es gibt keinen Grund für die Annahme, dass wir in der Praxis immer nur Y1 verwenden: Das wäre doch schön.
Ich habe diese Berechnungen jeweils 20.000 Mal durchgeführt und mir die Verteilungen von b1 unter OLS und TLS angesehen. Dann fügte ich ein paar weitere Änderungen hinzu. Zunächst reduzierte ich die Varianz des Rauschtextes in den X, was einer Verbesserung des Signal-Rausch-Verhältnisses in X entspricht. Außerdem führte ich eine Version durch, in der die X leicht negativ korreliert sind, um der Situation in Anwendungen zur Signaldetektion zu entsprechen, bei denen die anthropogenen und natürlichen Signale negativ korreliert sind.
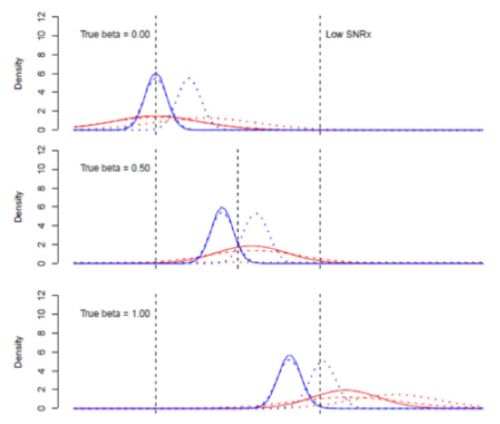
Die Arbeitsannahme im Bereich der Signaldetektion ist, dass die OLS-Schätzungen von b1 niedrig verzerrt, die TLS-Schätzungen jedoch unverzerrt sind. In der ersten Reihe von Ergebnissen waren die Verteilungen von b1 wie folgt:
OLS ist in blau und TLS in rot dargestellt. Eine durchgezogene Linie bedeutet, dass die abhängige Variable Y1 war, eine gestrichelte Linie bedeutet, dass sie YQ1 war und eine gepunktete Linie bedeutet, dass sie YQ2 war. Betrachtet man die OLS-Ergebnisse, so ist die Dämpfungsverzerrung multiplikativ, d. h. wenn der wahre Wert von b gleich Null ist, ist OLS unverzerrt. Es bleibt unverzerrt, wenn das Modell eine unabhängige erklärende Variable auslässt, aber wenn die ausgelassene Variable mit X1 korreliert ist (gestrichelte Linie), wird die OLS-Schätzung nach oben verzerrt. Wenn der wahre Wert von b ansteigt, zentriert sich die OLS-Schätzung unterhalb des wahren Wertes. Im unteren Feld, gepunktete Linie, heben sich die Verzerrung durch die Abschwächung und die Verzerrung durch die weggelassene Variable in etwa auf (gepunktete Linie), aber das ist nur ein Zufall und keine allgemeine Regel.
Die TLS-Ergebnisse sind anders. Zunächst einmal ist die Verteilung viel breiter, weil TLS weniger effizient ist. Wenn der wahre Wert von b gleich Null ist und es keine ausgelassenen Variablen gibt, ist die Verteilung auf Null zentriert. Wenn der wahre Wert von b ansteigt, führen alle drei Versionen der TLS-Regression zu positiv verzerrten Schätzungen.
Die positive Verzerrung ist nicht nur wegen des Risikos falsch positiver Ergebnisse von Bedeutung, sondern auch, weil die Größe des Koeffizienten selbst in die Berechnungen des „Kohlenstoffbudgets“ einfließt. Je höher der Koeffizientenwert ist, desto kleiner ist das „zulässige“ Kohlenstoffbudget, wenn der Punkt geschätzt wird, an dem die Welt ein bestimmtes Klimaziel überschreitet. Dies sind wichtige Berechnungen mit sehr großen globalen makroökonomischen Auswirkungen, so dass ich es beunruhigend finde, dass das Problem der positiven Verzerrung in TLS-basierten Fingerprinting-Regressionsergebnissen bisher nicht untersucht wurde.
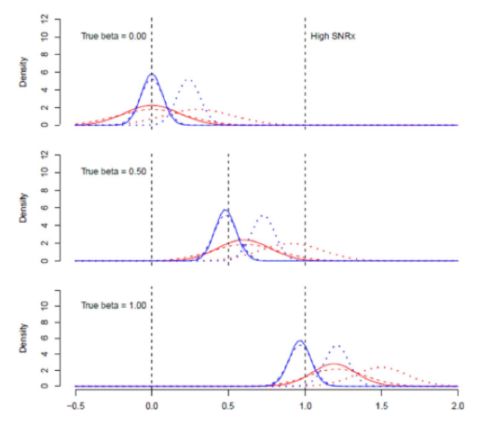
Für die nächste Gruppe von Schätzungen habe ich die Varianz des Rauschens auf den X-Werten reduziert, was ich als den Fall mit hohem SNRx bezeichne.
OLS nähert sich dem wahren Wert an, wenn es keine korrelierte weggelassene Variable gibt, was sinnvoll ist, denn wenn das Rauschen bei X gegen Null geht, nähern wir uns dem Fall, in dem OLS bekanntermaßen unverzerrt ist. Bei TLS ist diese Tendenz jedoch nicht zu beobachten, und die positive Verzerrung wird im Fall der weggelassenen Variablen sogar noch etwas größer. Dies ist keine gute Eigenschaft eines Schätzers: Wenn eine wichtige Rauschkomponente schrumpft, sollte man erwarten, dass er sich dem wahren Wert annähert.
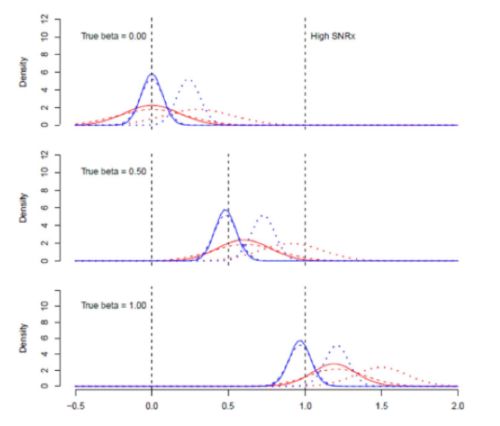
Als Nächstes habe ich den Fall betrachtet, in dem das Rauschen bei X und y gleich groß ist. Dies ist die optimale Konfiguration für TLS, da das angenommene Varianzverhältnis im Berechnungsalgorithmus dem tatsächlichen unbeobachtbaren Varianzverhältnis entspricht. Wenn das Regressionsmodell korrekt spezifiziert ist, ist TLS unverzerrt. Wenn jedoch eine Variable ausgelassen wird, selbst eine unkorrelierte, und der wahre Wert von Beta >0 ist, hat TLS eine Verzerrung nach oben. OLS hat eine Verzerrung nach unten, außer wenn Q2 fehlt, dann ist die Nettoverzerrung nach oben:
Ich habe zahlreiche andere Konfigurationen des Simulationsmodells untersucht und die Frage erörtert, welchem Schätzer der Vorzug zu geben ist. Die unterschiedlichen Ergebnisse spiegeln nicht die Wahl der Methode wider, sondern unterschiedliche Annahmen über die zugrundeliegenden Datenerzeugungsprozesse, und wenn der Forscher keine Ahnung hat, welche Methode den vorliegenden Datensatz am besten beschreibt, ist OLS trotz der bekannten Verzerrungen häufiger die bevorzugte Option als TLS. Ja, OLS liefert manchmal einen Koeffizienten, der gegen Null tendiert, aber das ist eine bekannte Verzerrung. TLS liefert in der Regel einen Koeffizienten mit einer positiven Verzerrung, und die Größe der Verzerrung ist zum Teil wegen der großen Varianz schwer vorherzusagen.
Interessanterweise geht die Präferenz des Schätzers eindeutig in Richtung OLS, wenn der wahre Wert von b gegen Null geht, da der Dämpfungsbias gegen Null geht und der TLS-Schätzer undefiniert wird. Das heißt, wenn wir die Nullhypothese testen, dass b=0 ist, mit anderen Worten, dass der Treibhauseffekt die beobachteten Klimaänderungen nicht erklärt, sollten wir uns nicht auf TLS verlassen, denn wenn die Nullhypothese wahr ist, würden wir nicht TLS, sondern OLS verwenden. Oder anders ausgedrückt: Wenn ein signifikantes Signalerkennungsergebnis von der Verwendung von TLS statt OLS abhängt, ist es kein robustes Ergebnis.
Die nächsten Schritte
Ich habe eine weitere Studie in Arbeit, in der ich die Folgen einer möglichen Korrelation der X-Werte untereinander im Detail untersuche. Ich habe einen vorläufigen Blick auf diesen Fall in das vorliegende Papier aufgenommen. Ich habe herausgefunden, dass OLS bei korrelierten Signalen immer noch eine dämpfende Verzerrung aufweist, selbst wenn der wahre Wert von b = 0 ist, und dass TLS eine positive Verzerrung aufweist, aber in diesem Fall wird die TLS-Verzerrung groß genug, um falsch positive Ergebnisse zu riskieren: nämlich einen scheinbar „signifikanten“ Wert von b, selbst wenn der wahre Wert Null ist.
Zusammenfassend komme ich zu dem Schluss, dass TLS im Allgemeinen eine Überkorrektur der Dämpfungsverzerrung vornimmt und dadurch zu große Signalkoeffizienten ergibt. Außerdem führt sie zu extrem instabilen Schätzungen mit großen Varianzen. Forscher sollten sich nicht auf TLS verlassen, um Rückschlüsse auf die Signalentdeckung zu ziehen, es sei denn, sie haben die erforderlichen Tests durchgeführt (wie in meinem Beitrag beschrieben), die belegen, dass TLS für den jeweiligen Kontext geeignet ist.
Außerdem sollten Klimawissenschaftler die Verwendung von Instrumentalvariablen als Lösung für das EIV-Problem in Betracht ziehen, da sie nachweislich unverzerrte und konsistente Ergebnisse liefern.
Hinweis: Als ich die Korrekturabzüge erstellte, sahen die Tabellen mit den Hauptergebnissen auf dem Bildschirm gut aus, aber die Druckversion ist fehlerhaft. Die Zeilen 1, 7 und 13 sollten jeweils um eine Zeile nach unten verschoben werden.
Link: https://wattsupwiththat.com/2022/06/02/biases-in-climate-fingerprinting-methods/
Übersetzt von Christian Freuer für das EIKE