Handreichung zum besseren Verständnis der Stefan-Boltzmann-Inversion

Vorwort der EIKE Redaktion

Der folgende Beitrag wird wieder eine heftige Diskussion unter einigen unserer Leser auslösen. Dies ist insofern unverständlich, als das doch wohl vorausgesetzt werden kann, dass – wie jeder aus eigenem Erleben weiß – die Sonne nur tagsüber scheint. Das muss als gesetzt akzeptiert werden. Was dann noch bleibt ist die Klärung der Frage: Sind die von der internationalen Klimawissenschaft gemachten Vereinfachungen der Bildung der Mittelwerte von Ein- und Abstrahlung über die Kugelfläche statt der Halbkugelfläche, bei der Ermittlung der der Erde zugestrahlten und abgestrahlten Energiemenge, zulässig oder nicht. Wären sie es, dann müsste es ein Leichtes sein, aus ihren Ergebnissen auch die Temperatur der real bestrahlten Halbkugel bei gleichzeitiger Abstrahlung durch die Vollkugel widerspruchsfrei und auf die Kommastelle genau herzuleiten. Bisher hat das aber niemand vermocht, zumindest nicht hier in dieser Leserschaft. Vielleicht regt der folgende Beitrag dazu an.

von Uli Weber

Obgleich es auf unserer Erde erwiesenermaßen Tag und Nacht gibt (Abbildungen 5 und 6) und sich die Relation zwischen beiden über den Jahresverlauf ständig verändert (Siehe Titelbild), wird mein hemisphärisches Stefan-Boltzmann-Modell von vielen Kommentatoren noch immer nicht verstanden und eine rein mathematische Tag=Nacht-Mittelung als Grundlage einer globalen 24h-S-B-Inversion bevorzugt.
Gerne wiederhole ich daher noch einmal die Widerlegungsanforderung für meinen hemisphärischen S-B-Ansatz aus WEBER (2017) hier auf EIKE über einen physikalischen Tag=Nacht-Beweis:

„Wenn also wissenschaftlich eindeutig nachgewiesen würde, dass die Gleichsetzung der Energiebilanz unserer Erde (Fläche einer Kugel) mit der strengen thermischen Gleichgewichtsforderung des Stefan-Boltzmann Gesetzes für die bestrahlte Fläche (Halbkugel) physikalisch korrekt ist, dann bin ich tatsächlich widerlegt.“

Dazu ein Zitat aus dem Artikel, „Ist „Klimawandel“ Wissenschaft oder Pseudo-Wissenschaft?“ von Andy May, übersetzt von Christian Freuer für das EIKE:

„Eine Hypothese, die durch kein denkbares Ereignis widerlegbar ist, ist nicht wissenschaftlich. Popper fragte sich 1919, worin sich Marxismus, Freud und Astrologie von wirklich wissenschaftlichen Theorien wie Newtons Gravitationsgesetz oder Einsteins Relativitätstheorie unterscheiden. Er erkannte, dass letztere getestet und als falsch nachgewiesen werden konnten. Inspiriert wurde er durch die Bestätigung von Einsteins Theorie durch Frank Dyson, Andrew Crommelin und Arthur Eddington während der Sonnenfinsternis 1919.“

Ich darf hier also in aller Bescheidenheit darauf verweisen, dass ich schon sehr frühzeitig einen Widerlegungsbeweis für mein hemisphärisches S-B-Modell eingefordert hatte. Trotz dieser Beweisanforderung ist mir bis heute kein wissenschaftlicher Nachweis für eine physikalische Gleichheit von Tag (@2PiR²) und Nacht (@2PiR²) bekannt geworden. Man ersetzt bei der konventionellen Stefan-Boltzmann-Inversion vielmehr weiterhin die Ungleichheit zwischen Tag und Nacht durch einen physikalisch bedeutungslosen rein mathematischen 24h-Durchschnittswert (@4PiR²) …

Nachfolgend nähern wir uns den theoretischen S-B-Grundlagen einmal über das Stefan-Boltzmann-Experiment. Das Stefan-Boltzmann-Experiment ist ein Standardexperiment in der physikalischen Ausbildung, das den Zusammenhang zwischen der Temperatur eines künstlich erhitzten Schwarzen Körpers und der von seiner Oberfläche abgegebenen spezifischen Strahlungsleistung im gemeinsamen und zeitlich unmittelbaren thermischen Gleichgewichtszustand beschreibt. Der Versuchsaufbau ist denkbar einfach:

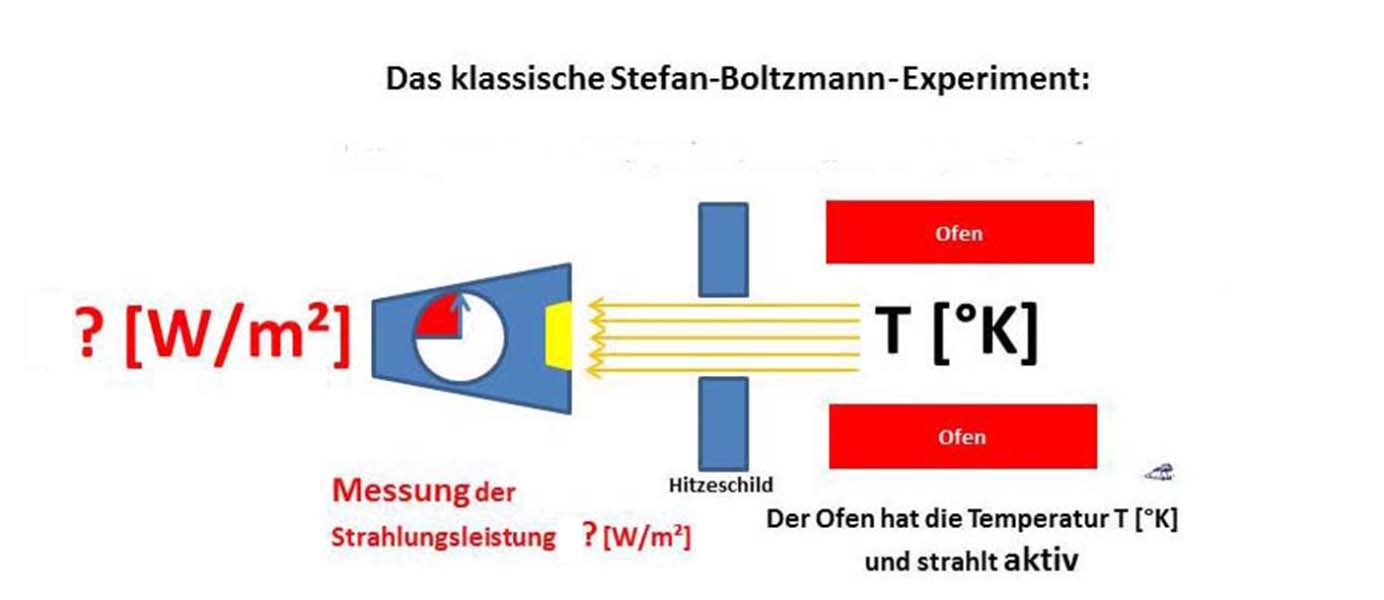
Abbildung 1: Das klassische Stefan-Boltzmann-Experiment, Ofen. Hitzeschild mit Blende und Messgerät

Beschreibung:

• Ein Rohrofen (rechts) wird auf eine bestimmte Temperatur erhitzt; der Schwarze Strahler wird dabei beispielsweise durch einen brünierten Messingzylinder dargestellt.
• Der Ofen hat eine konstante Temperatur und wird durch eine (ggf. gekühlte) Blende (Mitte) vom Meßgerät abgeschirmt.
• Die austretende Strahlungsleistung wird gemessen (links).

Das Stefan-Boltzmann-Gesetz lautet:

(1) P = σ _* A _* T⁴ oder S = P/A = σ _* T⁴
mit der Stefan-Boltzmann-Konstante σ = 5,670 10 ^-8 [W m^-2 K^-4]

und P = Strahlung in [W], A = Fläche [m²], T = Temperatur in [K],
S = spezifische Strahlungsleistung in [W/m²]

Die Systematik dieser physikalischen S-B-Beziehung wird sofort klar, wenn wir in der nachfolgenden Abbildung einmal vier unterschiedlich große Schwarzkörper mit gleicher Temperatur betrachten:

 

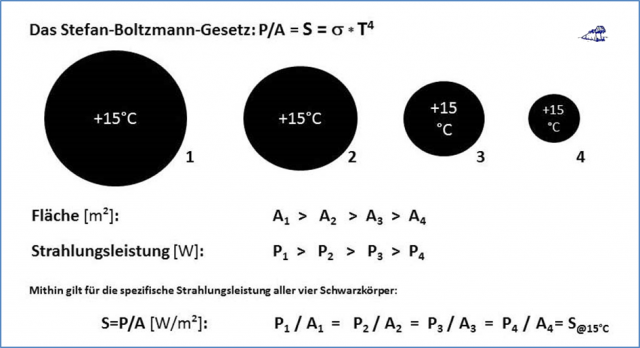
Abbildung 2: Zur Bedeutung der spezifischen Strahlungsleistung „S=P/A“ im S-B-Gesetz

Für einen beliebigen Schwarzen Körper mit einer Temperatur von +15°C gilt also immer:

Die SPEZIFISCHE Strahlungsleistung S_@15°C dieses Schwarzen Körpers beträgt 390 W/m².

Aus dieser Abbildung wird unmittelbar deutlich, dass die unterschiedlichen Strahlungsleistungen „P_i“ und die zugehörigen ABSTRAHLENDEN Flächen „A_i“ eindeutig zusammenhängen, weil sie für jeden Körper (1-4) eine augenblickliche spezifische Strahlungsleistung „S_@15°C“ definieren, die wiederum über das Stefan-Boltzmann-Gesetz eindeutig mit der Momentantemperatur des jeweiligen Körpers von 15°C verknüpft ist. Allein diese Temperatur (primär) bestimmt also die gleichzeitige spezifische Strahlungsleistung (sekundär) eines Schwarzen Körpers nach dem Stefan-Boltzmann-Gesetz:

Stefan-Boltzmann-Gesetz: Temperatur (primär) => Spezifische Strahlungsleistung (sekundär)

Jede Berechnung einer Temperatur (sekundär) aus der spezifischen Strahlungsleistung (primär) stellt demnach eine Inversion des Stefan-Boltzmann-Gesetzes dar, welche nur zulässig ist, wenn alle Randbedingungen, des S-B-Gesetzes streng erfüllt sind. Da diese aber nicht per se erfüllt werden, ist eine Inversion des S-B Gesetzes immer nur in physikalisch wohl definierten Fällen zulässig. Und diese Fälle orientieren sich wiederum an einer Umkehrung des S-B-Experimentes: Es muss sowohl die in diesem Moment ANGESTRAHLTE Fläche eindeutig definiert sein, als auch der Unterschied zwischen den Flächennormalen von einfallender Strahlung und beleuchteter Fläche (Neigung = Klima) vektoriell berücksichtigt werden.

Stefan-Boltzmann-Inversion: Spezifische Strahlungsleistung (primär) => Temperatur (sekundär)

Wohlgemerkt: JEDE Berechnung einer Temperatur aus der spezifischen Strahlungsleistung nach dem S-B-Gesetz stellt eine S-B-Inversion dar, auch die fehlerhafte konventionelle 24h-Tag=Nacht- Berechnung einer sogenannten „Gleichgewichtstemperatur“ von (-18°C) aus 235 W/m² @4PiR²!

Machen wir es uns mal ganz einfach und simulieren wir das S-B-Experiment bei 20°C Zimmertemperatur, 100°C, 200°C und 300°C. Die zugehörige spezifische Strahlungsleistung entnehmen wir jetzt einfach dem Stefan-Boltzmann-Gesetz:

• 20°C entspricht 293 K und 419 W/m²
• 100°C entspricht 373 K und 1100 W/m²
• 200°C entspricht 473 K und 2842 W/m²
• 300°C entspricht 573 K und 6119 W/m²

Der Zusammenhang zwischen Temperatur und spezifischer Strahlungsleistung nach dem Stefan-Boltzmann-Gesetz ist nachfolgend in Abbildung 1 dargestellt:

 

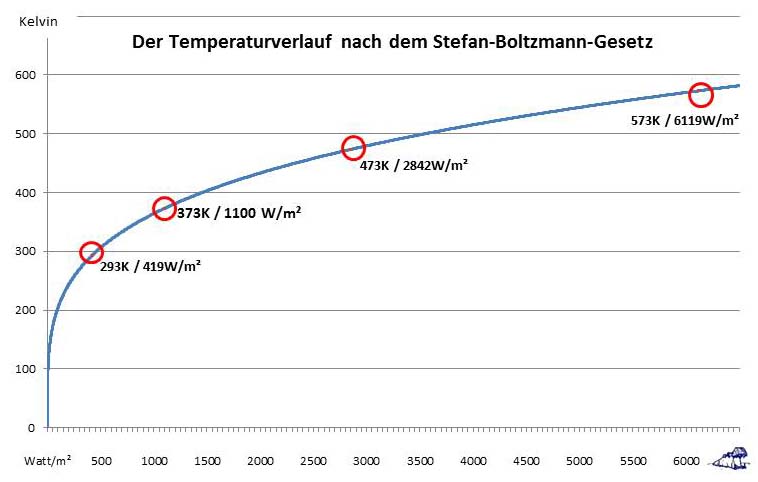Abbildung 3: Der Temperaturverlauf nach dem Stefan-Boltzmann-Gesetz (blaue Kurve) mit den 4 imaginären „Messpunkten“ bei 20°C, 100°C, 200°C und 300°C (rote Punkte im roten Kreis).

Sie werden bemerkt haben, dass die T⁴-Kurve bei 0 W/m² auf 0 Kelvin fällt. Das Dumme ist, dass im S-B-Experiment bei einer Raumtemperatur von 20°C keine Wertepaare unter 20°C/419 W/m² gemessen werden können. Denn der ganze Raum strahlt ja bei dieser Temperatur mit 419 W/m², selbst das Messgerät. Die S-B-Umgebungsgleichung trägt diesem Umstand Rechnung und das Stefan-Boltzmann-Gesetz in seiner allgemeinen Form lautet dann:

(2)

(Anmerkung: Die Gleichung 2 wurde am 8.6.22 vom Autor korrigert. Mit Dank an den aufmerksamen Leser Harde)

Alle Parameter wie in Gleichung 1 mit T₀ = Umgebungstemperatur

Und jetzt bilden wir aus unseren „Messpunkten“(schwarz) einmal Mittelwerte (rot):

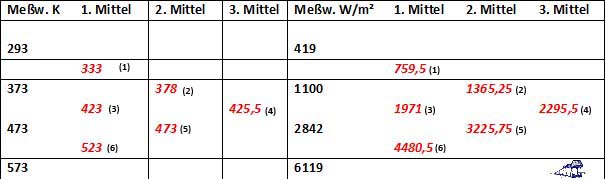
Tabelle 1: „Messwerte“ nach dem S-B-Gesetz und daraus abgeleitete Mittelwerte der 1. bis 3. Generation

Diese Mittelwerte (rot) fügen wir jetzt wiederum in die Stefan-Boltzmann-Funktion (Abb.1) ein und erhalten:

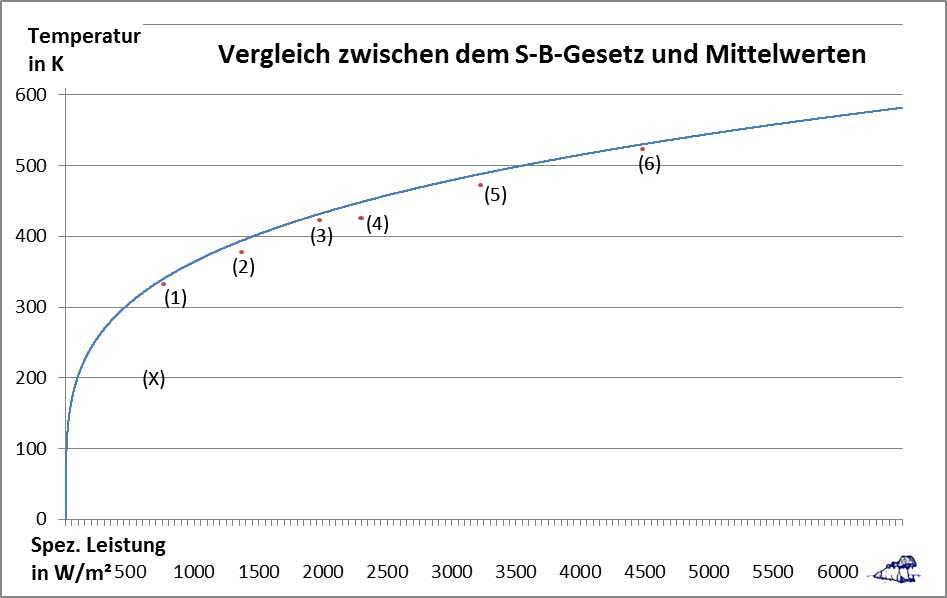
Abbildung 4: Vergleich des Temperaturverlaufs nach dem Stefan-Boltzmann-Gesetz (blaue Kurve) mit den berechneten Mittelwerten aus Tabelle 1 (rote Punkte 1 bis 6). „(X)“ ist der Mittelwert aus der vorgeblichen nächtlichen Oberflächentemperatur in der konventionellen S-B-Inversion von 0K und der solar induzierten theoretisch möglichen Maximaltemperatur (Näheres im Text nach Abbildung 7).

In Abbildung 4 ist deutlich zu erkennen, dass die berechneten Mittelwerte nicht auf die Stefan-Boltzmann-Funktion fallen. Vielmehr entfernen sich die 3 Mittelwert-Generationen sukzessive von der blauen Kurve: 1. Generation (Punkte 1, 3 und 6), 2. Generation (Punkte 2 und 5), 3. Generation (Punkt 4). Die Differenz der linearen Durchschnittswerte zur Stefan-Boltzmann-Funktion wird also umso größer je größer die Spreizung der beteiligten Einzelwerte ist. Bei einer T⁴-Funktion sollte dieses Ergebnis eigentlich nicht weiter verwundern.

Wir leben in einer Zeit, wo Meinungen als Fakten verkauft werden, und man Fakten als Meinungen diffamiert. Bilden Sie sich also selbst eine Meinung, indem Sie die Fakten bewerten:

Abbildung 5: Die Inversion des Stefan-Boltzmann-Gesetzes

Unsere Erde wird lediglich auf ihrer Tagseite von der Sonne angestrahlt

Zwischenfrage: Sind die beiden Körper in Abbildung 6 physikalisch wirklich absolut identisch? – Es kann doch nur ein physikalisch korrektes Modell geben, entweder links oder rechts in Abbildung 6:

 

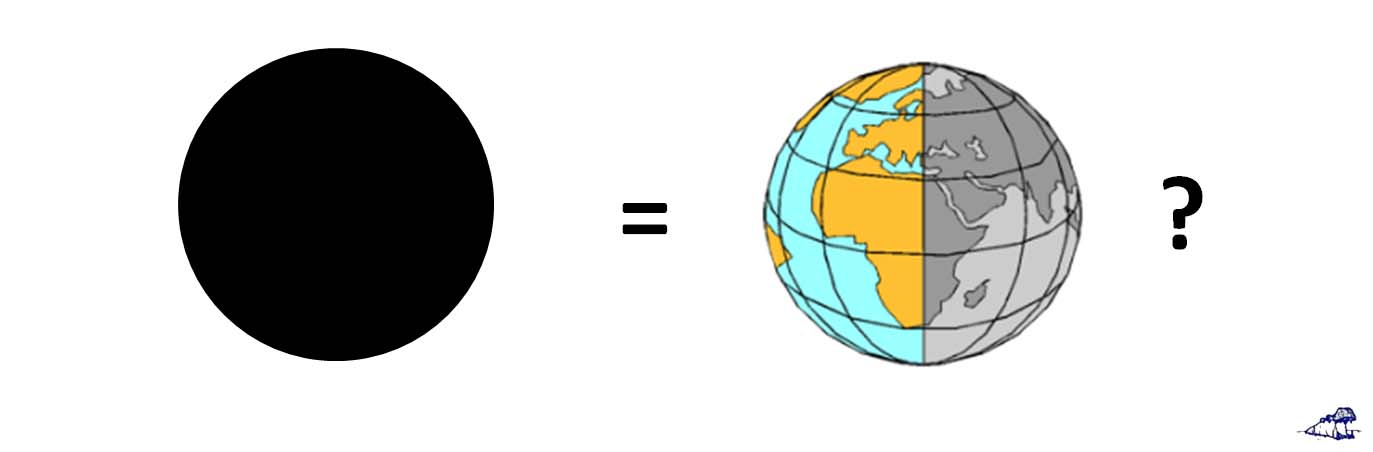Abbildung 6: Vergleich eines selbstleuchtenden Sterns (Schwarzkörper) mit einem Planeten (Erde)

Links selbstleuchtender Stern (ohne Tag und Nacht), ABSTRAHLUNG: 235W/m² @ 4PIR² bei -18°C
Rechts hemisphärisch beleuchteter Planet (unsere Erde mit Tag und Nacht)
Solare EINSTRAHLUNG = Σ_i (940W/m² _* cos ϕ_i)/i @ 2PIR² über eine Halbkugel (-Pi/2 bis +Pi/2) bei einer Durchschnittstemperatur von +15°C mit ϕ_i=örtlicher Zenitwinkel der Sonne

Nun, der S-B Durchschnitt der Temperatur wird für den selbstleuchtenden Stern (Schwarzkörper) im konventionellen Ansatz mit -18°C angegeben, der gemessene Durchschnitt für unsere Erde beträgt aber ca. 15°C. Der Klima-Mainstream bewertet die beiden Körper aus Abbildung 6 also als physikalisch völlig gleich und erklärt die Temperaturdifferenz mit einem sogenannten „natürlichen atmosphärischen Treibhauseffekt“ von 33 Grad. Wir können also verkürzend zusammenfassen, dass der physikalische Unterschied zwischen einem selbstleuchtenden aktiven Stern und einem halbseitig bestrahlten passiven Planeten ein sogenannter „atmosphärischer Treibhauseffekt“ sein soll.

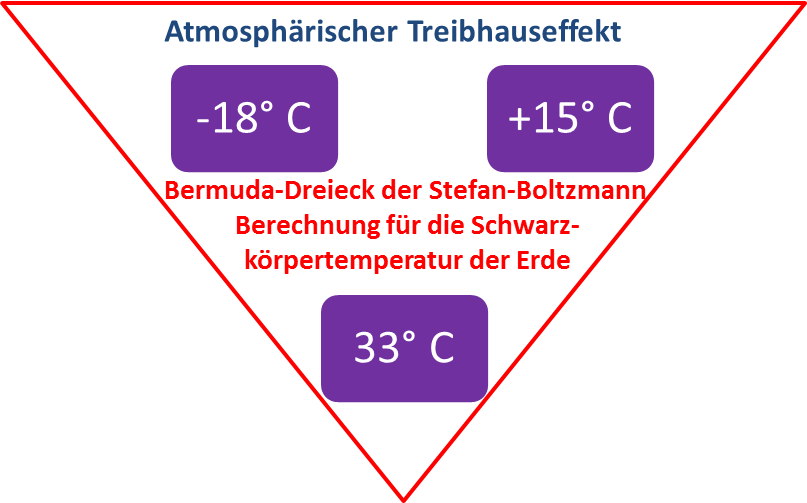
Abbildung 7: Das Bermuda-Dreieck einer fehlerhaften Inversion des Stefan-Boltzmann-Gesetzes: „Gleichgewichtstemperatur“ (-18°C), (+15°) real „gemessener“ Durchschnitt, 33° Differenz=THE

Der sogenannte „atmosphärische Treibhauseffekt“ entstammt also dem Bermuda-Dreieck einer physikalisch fehlerhaften Inversion des Stefan-Boltzmann-Gesetzes. Das ist schon komisch, denn allein der Durchschnitt aus minimaler und maximaler Temperatur bei einem halbseitig bestrahlten Körper wie der Erde sieht folgendermaßen aus: Die maximal mögliche solar induzierte Temperatur auf unserer Erde beträgt bei vertikalem Sonnenstand ohne Albedo 394 Kelvin, während die nächtliche Oberflächentemperatur im konventionellen S-B-Ansatz mit 0 Kelvin angenommen wird. Beides ergibt einen Mittelwert von (394+0)K/2 = 197 [K] bei (1367+0)W/m²/2 = 683,5 [W/m²], wie er als „(X)“ in Abbildung 4 eingetragen ist.

Das Stefan-Boltzmann-Gesetz verknüpft Temperatur und spezifische Strahlungsleistung eines Körpers im Moment der ABSTRAHLUNG und gilt daher ausschließlich „just in time“. Es wird also aus dem Stefan-Boltzmann-Experiment unmittelbar deutlich, dass eine Mittelung über die Tag- und Nachtseite unserer Erde gar nicht der Stefan-Boltzmann-T⁴-Beziehung gehorchen kann (S. auch Anhang). Eine Inversion des Stefan-Boltzmann-Gesetzes für die Temperaturbestimmung auf der Erde darf vielmehr nur Flächen einschließen, die genau im Augenblick der solaren ABSTRAHLUNG auch tatsächlich ANGESTRAHLT werden:

Um es hier noch einmal barrierefrei auszudrücken: Nur die ANGESTRAHLTE Fläche zählt bei einer S-B-Inversion. Denn wenn man die unbeleuchtete Nachtseite unserer Erde als ANSTRAHLUNGSFLÄCHE in die Temperaturberechnung einer Stefan-Boltzmann-Inversion einschließt, dann könnte man ebenso gut die unbeleuchtete Tischplatte des Experimentiertisches als ABSTRAHLUNGSFLÄCHE in das Stefan-Boltzmann-Experiment einbeziehen.

Zum besseren Verständnis meiner hemisphärischen Temperaturberechnung für unsere Erde verweise ich abschließend auf diesen Text, diesen Artikel und/oder dieses Buch.

Anhang: Die Berechnungen von Professor Dr. G. Gerlich aus seinem Vortrag zur Treibhaus-Kontroverse, Leipzig, 9./10. Nov. 1995 mit einer Hervorhebung:

Wir haben gesehen, dass lediglich die Tagseite der Erde (2πR²) im Strahlungsgleichgewicht zwischen Sonne und Erde mit dem Stefan-Boltzmann-Gesetz betrachtet werden darf. Aber auch Gerlich betrachtet bei seiner Temperaturberechnung fälschlich die gesamte Erdoberfläche und schließt dabei die Nachtseite mit 0 Kelvin ein. Von daher muss diese Lösung von Gerlich (1995) für die gesamte Erdoberfläche (4πR²) auf die Tagseite der Erde (2πR²) reduziert bzw. das Ergebnis verdoppelt werden:

Temperatur Tagseite = Lösung Gerlich _* 4πR² / 2πR² = 2 _* Lösung Gerlich

meine hemisphärische Korrektur der Integrallösung von Gerlich (1995)

Folglich verdoppelt sich die Lösung von Gerlich (1995) für die physikalische Temperatur auf Tagseite der Erde zu T_phys-hem = 2_*(-129°C =144 K) = 2_*144 K = 288 K oder 15°C

Ausführliche Herleitung: Anmer­kungen zur hemisphä­rischen Mittelwert­bildung mit dem Stefan-Boltzmann-Gesetz | EIKE – Europäisches Institut für Klima & Energie (eike-klima-energie.eu)