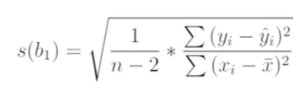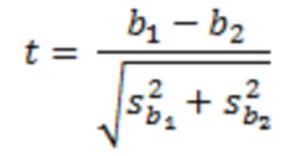UN: „Die Welt geht unter“ – einen Knick* zeigende Analysen sagen etwas Anderes
Dr. Warren Smith
[*Der Begriff „Kink“ wird im Folgenden mit „Knick“ übersetzt. Eine bessere Übersetzung war nicht zu finden. Das Ganze erinnert stark an die Arbeiten von Öllinger, der darin Temperaturänderungen in Stufen heraus analysiert hat. A. d. Übers.]
Executive Summary:
Der jüngste UN-Bericht, in dem dringend Maßnahmen zur Verringerung des Katastrophenrisikos gefordert werden, beruht auf falschen Analysen und sogar einfachen Rechenfehlern.
Es wird ein Instrument zur Analyse nichtlinearer „Knicke“ in Zeitreihendaten entwickelt und vorgestellt, mit dem „aktuelle Trends“ in der Katastrophenhäufigkeit ermittelt werden können, die sich stark von den vom United Nations Office for Disaster Risk Reduction behaupteten langfristigen Trends unterscheiden.
Introduction:
Vor kurzem hat dieses Büro einen 256-seitigen Bericht mit dem Untertitel „Transforming Governance for a Resilient Future“ [etwa: Transformation der Staatsführung für eine widerstandsfähige Zukunft] veröffentlicht. Der Bericht fordert eine sofortige „Neuverdrahtung“ der multinationalen Governance-Strukturen, um sich auf eine prognostizierte Verdreifachung der extremen Wetterereignisse zwischen 2001 und 2030 und einen raschen Anstieg der allgemeinen Katastrophen weltweit von etwa 400 im Jahr 2015 auf 560 pro Jahr im Jahr 2030 vorzubereiten. In dem Bericht werden dringende Maßnahmen zur Bewältigung dieser zunehmenden Katastrophen dargelegt, wobei massive Investitionen und internationale Zusammenarbeit sowie eine Neufassung der Regeln, nach denen wir leben, gefordert werden.
Die „Herausforderung“, vor der die gesamte Menschheit steht, wird in mehreren Schlüsseldiagrammen dargestellt, die sowohl in dem Papier als auch – in bunterer Form – auf der UN-Website mit einer Zusammenfassung der Studie zu finden sind. Das heißt, die gesamte Studie basiert auf der Prämisse, dass die Häufigkeit und Schwere von Katastrophen zunimmt und die Menschheit gefährdet ist, wenn wir keine massiven Maßnahmen ergreifen, um uns vorzubereiten.
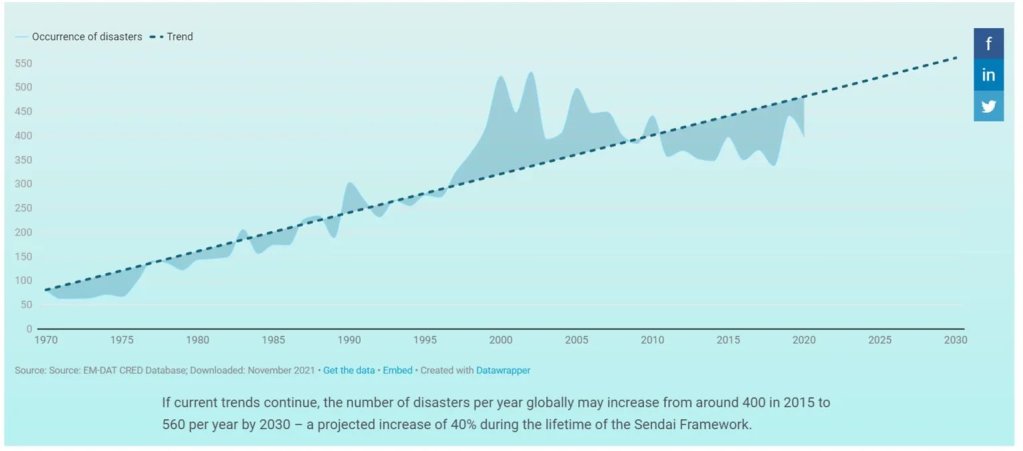
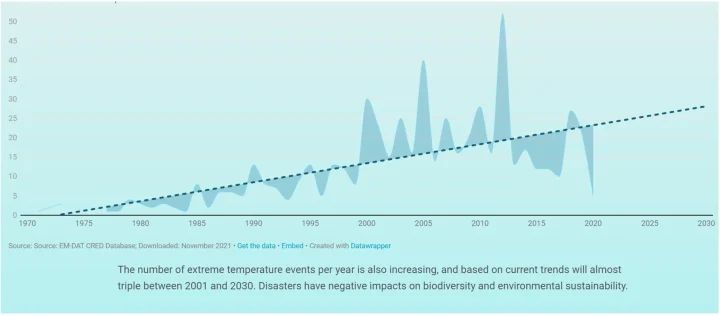
Die grundlegende Grafik, die das Problem beschreibt, ist im Folgenden wiedergegeben und stammt von der UN-Website:
Wie jedem erfahrenen Datenanalysten sofort klar sein sollte, stellt die dargestellte lineare Regression nach der Methode der kleinsten Quadrate die zugrunde liegenden Daten nicht gut dar. Insbesondere der „Fehler“ in der Grafik (die Abweichung des geschätzten Wertes von den tatsächlichen Werten) nimmt nach den späten 1990er Jahren dramatisch zu. Dies deutet darauf hin, dass die Linearität der Daten irgendwann in den späten 1990er Jahren zusammenbricht, so dass Prognosen, die weitgehend auf früheren Daten beruhen, ungültig werden.
Glücklicherweise enthält die Website einen Link zu den Daten, die zur Erstellung dieser recht alarmierenden Grafik verwendet wurden, so dass unabhängige Analysen möglich sind.
Es ist zwar verlockend, eine Linie von den Daten um 1998 diagonal nach unten zu ziehen und daraus den Schluss zu ziehen, dass Katastrophen tatsächlich seltener werden, aber ein solcher Ansatz ist nicht konsequent genug und ebenso anfällig für die gleiche Art von spitzfindigen Fehlern und Verzerrungen, die zur Erstellung dieser Grafik geführt haben. Es bedarf eines strengeren statistischen Ansatzes, um festzustellen, wann es unangemessen ist, einen Datensatz als „linear“ zu behandeln, und wann es angemessener wäre, den Datensatz in mehr als eine Linie aufzuteilen, um ihn separat zu schätzen.
Als Antwort darauf habe ich eine solche Technik entwickelt, die ich „Knick-Analyse“ nenne. Die Technik der Knick-Analyse wird in der zweiten Hälfte dieser Studie im Detail beschrieben, und eine Diskussion über dieses Hilfsmittel (das auch sehr gut für die Analyse von Trends in Klimadaten geeignet ist) ist willkommen. Das für diese „Knick-Analyse“ entwickelte Hilfsmittel wurde dann auf die von der UNO vorgelegten Daten angewandt, um festzustellen, ob ihre Anwendung der linearen Regression zur Vorhersage künftiger Katastrophenraten angemessen war oder nicht.
Knick-Analyse angewendet auf den UN-Katastrophen-Datensatz
Gesamtzahl globaler Katastrophen
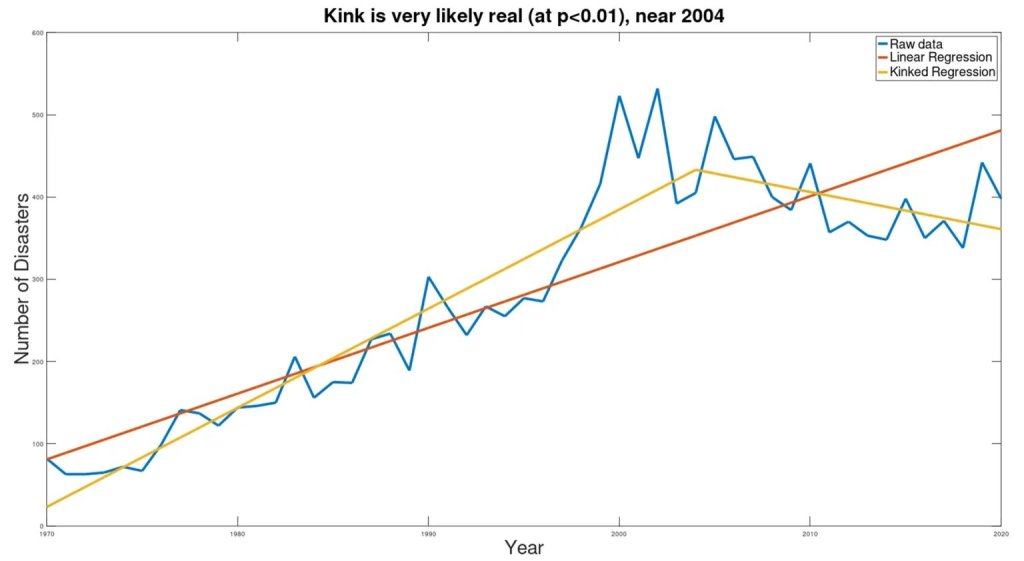
Die Anwendung der Knick-Analyse (das weiter unten im Detail beschrieben wird) auf die Katastrophen-Daten aus dem UN-Bericht führte zu den folgenden Ergebnissen, die sich von den UN-Schlussfolgerungen stark unterscheiden:
Die blaue Linie stellt die Rohdaten dar, die braune Linie ist die Schätzung der UNO, und die gelben Linien zeigen die geknickten Trends, die sich aus den Daten ergeben.
Statistisch gesehen ist das Vorhandensein des Knicks mit p<0,000005 äußerst signifikant. Der Knick wurde um das Jahr 2004 festgestellt, aber die Konfidenzgrenzen für das tatsächliche Jahr des Knicks sind noch nicht definiert (was bedeutet, dass eine Suche nach dem Mechanismus zur Erklärung dieses Knicks auf einige Jahre vor oder nach 2004 konzentriert werden sollte). Durch die Einführung des Knicks verringert sich der gepoolte Standardfehler um 58 % im Vergleich zum Standardfehler der einfachen linearen Regression, die im UN-Bericht erscheint. Die Verringerung des Standardfehlers, gepaart mit der statistischen Signifikanz des Unterschieds in den Steigungen der beiden Linien (vor und nach dem Knick), zeigt, dass das geknickte Modell die Daten viel besser erklärt als das lineare Modell.
Die wichtigste Erkenntnis dabei ist, dass die Häufigkeit von Katastrophen im Gegensatz zu den Behauptungen des UN-Berichts offenbar abnimmt. Während der UN-Bericht auf der Grundlage der fehlerhaften Anwendung eines einfachen linearen Regressionsmodells die unheilvolle Behauptung aufstellt, dass „bei Fortsetzung der derzeitigen Trends die Zahl der Katastrophen pro Jahr weltweit von etwa 400 im Jahr 2015 auf 560 pro Jahr im Jahr 2030 ansteigen könnte – ein prognostizierter Anstieg um 40% – zeigt die Knick-Analyse, dass der derzeitige Trend ganz anders aussieht als dargestellt, und dass die Zahl der Katastrophen pro Jahr höchstwahrscheinlich auf 158 pro Jahr zurückgehen wird, was einem Rückgang um mehr als 60 % und damit wieder dem Niveau von 1980 entspricht. (Natürlich kann sich ein rückläufiger Trend nicht unbegrenzt fortsetzen und muss sich irgendwann verlangsamen und aufhören, aber es bleibt dabei, dass die alarmistische UN-Behauptung über den „aktuellen Trend“ völlig irreführend ist und der panische Bericht, in dem sofortige Maßnahmen gefordert werden, völlig fehlgeleitet ist).
Dürren
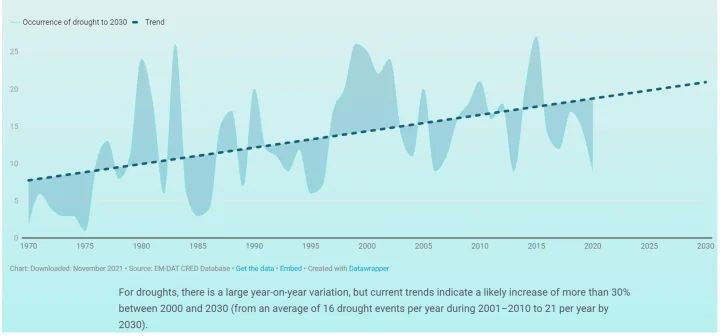
Der UN-Bericht prophezeit auch die für das Jahr 2030 zu erwartende Dürre und stellt die folgende Grafik vor, in der behauptet wird, dass die Dürre „von durchschnittlich 16 Dürreereignissen pro Jahr im Zeitraum 2001-2010 auf 21 pro Jahr im Jahr 2030 steigen wird“.
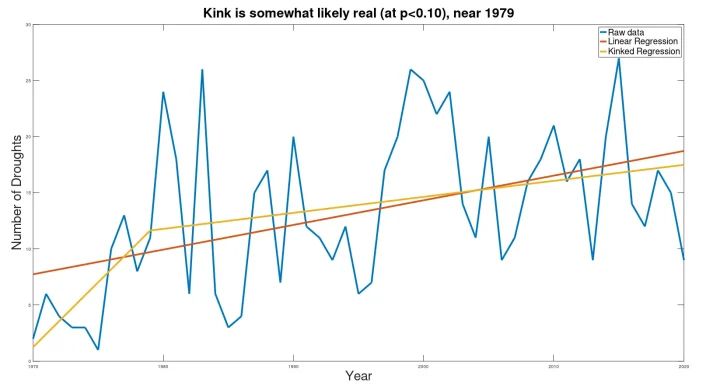
Die Variabilität von Jahr zu Jahr ist in diesem Datensatz viel höher, mit einer gewissen offensichtlichen Konjunkturabhängigkeit. Vielleicht aufgrund der größeren Variabilität liefert die Knick-Analyse nur wenig aussagekräftige Ergebnisse, denen nicht zu trauen ist. Ich füge das nachstehende Diagramm nur der Vollständigkeit halber bei:
Die hier dargestellten Ergebnisse unterscheiden sich nicht wesentlich von den von den UN veröffentlichten Ergebnissen.
Extreme Temperaturereignisse
Der UN-Bericht enthält auch ein Diagramm, das die Zunahme „extremer Temperaturereignisse“ anzeigt und behauptet, dass sich diese Ereignisse zwischen 2001 und 2030 „fast verdreifachen“ werden. (Es ist anzumerken, dass den UN-Daten zufolge die tatsächliche Zahl der extremen Temperaturereignisse im Jahr 2001 bei 23 lag, während sie für das Jahr 2030 nur 28 derartige Ereignisse vorhersagen, was einem Anstieg von nur 13 % entspricht. 13 % sind natürlich NICHT „fast das Dreifache“. Selbst wenn wir dem Autor Glauben schenken und zur Kenntnis nehmen, dass die Trendlinie im Jahr 2001 bei 14 lag, können die für 2030 vorhergesagten 28 Ereignisse nicht als „fast verdreifacht“ bezeichnet werden. Auch wenn der reich bebilderte Bericht mit seinen Diagrammen und Schaubildern dazu verleitet, den Schlussfolgerungen des Berichts Glauben zu schenken, belasten einfache Rechenfehler wie dieser die Glaubwürdigkeit).
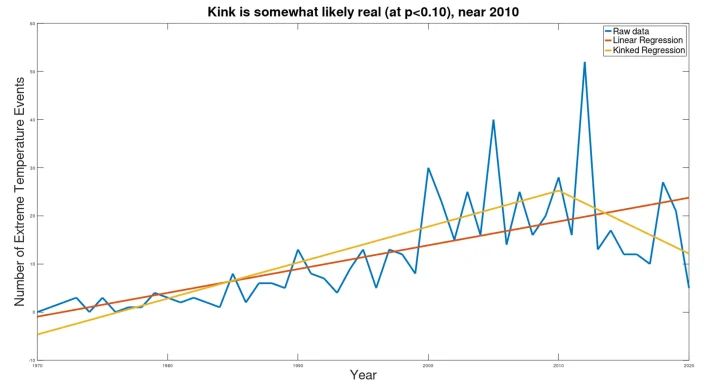
Während der UN-Bericht eine stetig steigende Tendenz aufweist, zeigt die Knick-Analyse ein ganz anderes Bild:
Auch wenn die Signifikanz nur schwach ist (p=0,083, mit einer Gesamtverringerung des gepoolten Standardfehlers von nur 17,4 % gegenüber der einfachen linearen Regression), ist der „aktuelle Trend“ erneut rückläufig, was darauf hindeutet, dass der zukünftige Trend höchstwahrscheinlich rückläufig sein wird. Trotz der Behauptung, dass sich die Zahl der extremen Temperaturereignisse zwischen 2001 und 2030 verdreifachen wird, war die Zahl der extremen Temperaturereignisse in sieben der letzten acht Jahre geringer als im Jahr 2001 (im Durchschnitt 36 % weniger extreme Temperaturereignisse als 2001). Der in den aktuellen Daten festgestellte Abwärtstrend ist zwar nicht nachhaltig (da die Projektion dieses Trends auf 2030 eine Zahl unter Null ergeben würde), aber die Statistiken belegen einen anhaltenden Abwärtstrend, so dass die beste Schätzung für 2030 keine „Verdreifachung“ der Häufigkeit gegenüber 2001 ist, wie im UN-Bericht behauptet wird, sondern eher eine wesentlich geringere Häufigkeit als 2001.
Schlussfolgerung
Die Motivation für den dringenden Handlungsaufruf der UNO wird auf ihrer Website dargelegt, die eine Zusammenfassung des Berichts „Transforming Governance for a Resilient Future“ enthält. Die Motivation für den Handlungsaufruf wird in den drei oben genannten Grafiken deutlich, die dem Bericht zufolge immer häufiger auftretende Katastrophen zeigen, die eine Änderung der „Governance-Systeme“ (einschließlich einer „Überarbeitung der staatlichen Lenkung“, um mehr staatliche Kontrolle zu ermöglichen) erfordern. Glücklicherweise scheint es so, als ob die Risikoanalysen der UN, die sich auf ihre Grafiken stützen, völlig falsch sind. Die Dringlichkeit dramatischer Maßnahmen, die in diesem Bericht gefordert wird, beruht ausschließlich auf analytischen Fehlern und sogar krassen Rechenfehlern. Dieser UN-Bericht ist daher nicht vertrauenswürdig und muss zurückgewiesen werden. Die mangelnden statistischen (und sogar rechnerischen) Fähigkeiten in diesem Bericht lassen Zweifel an anderen UN-Studien und statistischen Berichten aufkommen.
[Hervorhebung vom Übersetzer]
Teil II
Kink Analysis (Knick-Analyse)
[Das ist sozusagen der theoretische Teil. Wegen der nach Ansicht des Übersetzers grundlegenden Bedeutung dieses Verfahrens, wird es hier mit übersetzt. A. d. Übers.]
Die grundsätzliche Frage lautet: Ist es möglich, genau festzustellen, ob es in einem Zeitreihendatensatz einen „Knick“ gibt oder nicht (wie in den oben vorgestellten UN-Daten) und wo dieser Knick liegt? Zwar haben Datenanalysten das Vorhandensein von Trendumkehrungen (z. B. bei Klimadaten) oft „ins Auge gefasst“, doch damit eine Analyse genau ist, muss sie objektiv sein, d. h. subjektive Faktoren, die manchmal die Voreingenommenheit des Analysten widerspiegeln, müssen entfernt werden. Somit stellt sich die Frage: „Kann ein ‚Knick‘ in einer Zeitreihe durch eine objektive statistische Methode ermittelt werden?“
Als Antwort auf diese Frage wurde das nachstehend beschriebene Verfahren entwickelt:
1. Nehmen wir an, dass ein Änderungspunkt (ein „Knickpunkt“) im Datensatz vorhanden sein könnte. Dann teilen wir für jeden Punkt im Datensatz (als „Knickpunkt-Kandidat“ bezeichnet) den Datensatz an diesem Punkt auf (wobei der Knickpunkt-Kandidat in beiden erzeugten Datensätzen vorhanden ist) und führen Regressionen an den Daten vor und nach dem Knickpunkt-Kandidaten durch, wobei die Verbindung zwischen den beiden Liniensegmenten kontinuierlich sein muss. (In dieser Arbeit verwende ich die lineare Regression nach der Methode der kleinsten Quadrate unter Verwendung von Octave mit einigen Datentransformationen, um sicherzustellen, dass die beiden Liniensegmente kontinuierlich zueinander sind).
2. Dann berechnen wir für jeden Knickpunkt-Kandidaten den gepoolten Schätzfehler für den gesamten Datensatz. (Da jedes Liniensegment den Knick-Kandidaten enthält, wird der Fehler am Knick-Kandidaten selbst doppelt gezählt, was eine Einschränkung für die Verwendung dieses Punktes darstellt und so eine Überanpassung verhindert).
3. Man wähle den Knickpunkt, der den Gesamtfehler minimiert. An diesem Punkt lässt sich der Umfang der Verringerung des gepoolten Schätzfehlers (im Vergleich zu einer einzelnen linearen Regression) leicht berechnen, was zeigt, dass das Knicklinienmodell dem Datensatz besser entspricht als eine einzelne lineare Regression.
4. Danach verwenden wir einen t-Test, um zu berechnen, ob die beiden Liniensegmente unterschiedliche Steigungen haben, und akzeptieren den Knickpunkt als tatsächlichen Knickpunkt, wenn der t-Test anzeigt, dass die Steigungsunterschiede der erzeugten Liniensegmente statistisch unterschiedlich sind.
Dazu ermitteln wir den Standardfehler in der Schätzung jeder Steigung unter Verwendung der Standardgleichung:
Daraus berechnet sich die t-Statistik folgendermaßen, wieder unter Anwendung der bekannten Gleichung:
5. Prüfung der Signifikanz der t-Statistik mit Hilfe von Freiheitsgraden = Gesamtzahl der Datenpunkte im Satz minus 3. (Normalerweise würde man beim Vergleich der Steigungen zweier Linien 4 Freiheitsgrade in den Linien verbrauchen, aber die Verbindung ist darauf beschränkt, am Kandidatenpunkt kontinuierlich zu sein, so dass nur 3 Freiheitsgrade verbraucht werden).
6. Akzeptiere, dass die Linie „geknickt“ ist, wenn der t-Wert hochsignifikant ist (p<0,01), ziehe in Betracht, dass ein Knick vorhanden sein könnte, wenn der t-Wert schwach signifikant ist (p<0,10), und lehne die Linie andernfalls als „geknickt“ ab.
Ich habe ein Octave/Matlab-Programm geschrieben, um die oben beschriebenen Berechnungen durchzuführen, und es an simulierten Datensätzen mit linearen Daten und überlagertem Gauß’schen Rauschen getestet. In 20 Versuchen erbrachte das Programm die erwarteten Ergebnisse: ein falscher Knick auf dem Niveau von p=0,10, ein falscher Knick auf dem Niveau von p=0,05 und kein falscher Knick auf dem Niveau von p=0,01.
Wenn hingegen simulierte Datensätze mit geknickten Signalen mit überlagerndem Gauß’schen Rauschen getestet wurden, wurden die Knicke trotz erheblichen Rauschens mit starker statistischer Signifikanz gefunden. Im Folgenden werden zwei Beispiele angeführt:
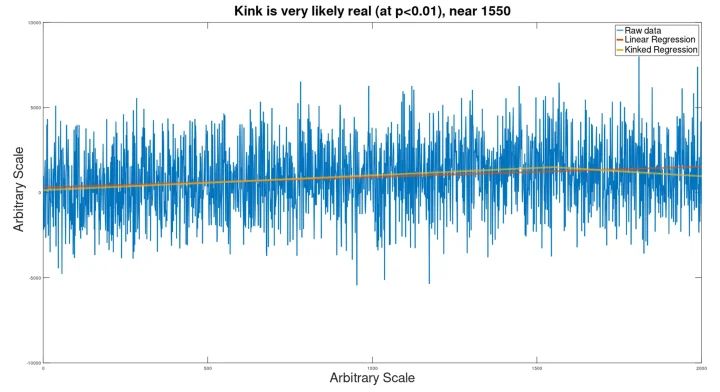
Beispiel 1: ein großer Datensatz (2000 Datenpunkte)
Als Grundlage diente ein Signal wie das unten Abgebildete:
Dazu wurde ein Gauß’sches Rauschsignal hinzugefügt, und das Ergebnis wurde durch den Knick-Analysator geleitet, um zu sehen, ob das Signal gefunden werden würde.
Trotz des extremen Rauschens wurde der Knick (der für das Auge eigentlich nicht wahrnehmbar ist) entdeckt (bei p=.005), so dass eine geknickte Regressionslinie entstand, die dem verborgenen Eingangssignal sehr nahe kam.
Die Lage des Knicks war etwas falsch (bei 1550 statt 1500).
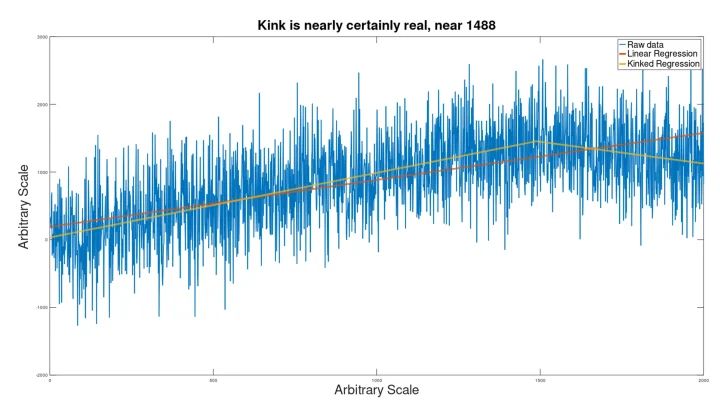
Mit weniger Rauschen wurde die Lage des Knicks jedoch genauer bestimmt:
Hier ist die Existenz des Knicks für das menschliche Auge einigermaßen wahrnehmbar, aber statistisch völlig unbedenklich, mit einem p-Wert von 7e-24.
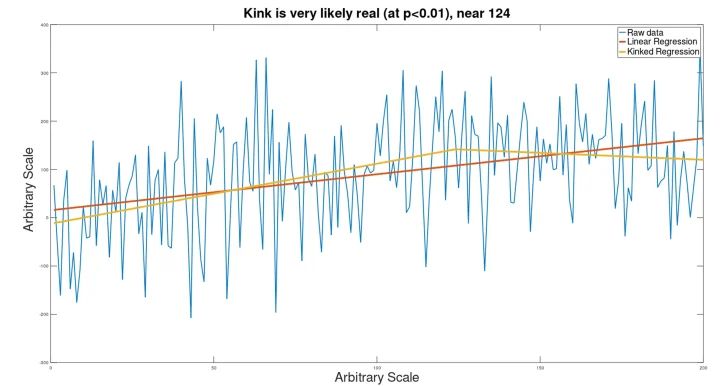
Beispiel 2: Kleinerer Datensatz (200 Punkte)
Auf einen ähnlichen geknickten Datensatz wie oben wurde Gauß’sches Rauschen angewendet, gefolgt von einer Knickanalyse. Das Ergebnis ist unten dargestellt:
Obwohl der Knick in diesem Datensatz für das Auge nicht sichtbar ist, konnte die Analyse dennoch erkennen, dass es einen Knick gibt (obwohl er in der Nähe von Punkt 124 statt von Punkt 150 berechnet wurde).
Mit weniger Rauschen wird der Ort des Knicks genauer identifiziert:
Beschränkungen:
Mit dieser Technik wird eine gekrümmte Linie (z. B. eine logarithmische Kurve) als Knick erkannt. Außerdem habe ich derzeit keine statistische Methode, mit der ich ein Vertrauensintervall für die Lage des Knicks festlegen könnte.
Schlussfolgerung:
Es ist zu erwarten, dass dieses Verfahren bei der Analyse politischer Maßnahmen angewendet wird, um nach Veränderungen von Trends in der Klimatologie, der Kriminalitätsstatistik usw. zu suchen, wo politische Eingriffe und andere Faktoren dazu führen, dass sich die Trends im Laufe der Zeit verändern (was eine einfache lineare Regression unangemessen macht).
Link: https://wattsupwiththat.com/2022/05/14/un-the-world-is-going-to-end-kink-analysis-says-otherwise/
Übersetzt von Christian Freuer für das EIKE