AR6 und Meeresspiegel Teil 3: eine statistisch valide Vorhersage
In Teil 1 dieser Serie [auf Deutsch beim EIKE hier] haben wir die Daten und Analysen untersucht, die im AR6 zur Untermauerung der Schlussfolgerung vorgelegt worden waren, dass sich der Meeresspiegelanstieg beschleunigt. In Teil 2 [auf Deutsch beim EIKE hier] haben wir eine ernsthafte Untersuchung der Beobachtungsdaten für den Meeresspiegelanstieg der letzten 120 Jahre und der modellierten Komponenten dieses Anstiegs vorgenommen. In Teil 1 kamen wir zu dem Schluss, dass die im AR6 präsentierten statistischen Beweise für die Beschleunigung grob und unausgegoren waren. In Teil 2 haben wir gesehen, dass der Fehler sowohl bei den Schätzungen des Meeresspiegelanstiegs als auch bei der Schätzung der Komponenten dieses Anstiegs sehr groß ist. Der Fehler schloss eine zuverlässige Bestimmung der Beschleunigung aus, aber die Daten zeigten eine etwa 60-jährige Oszillation der Anstiegsrate des Meeresspiegels, die mit bekannten natürlichen Ozeanzyklen übereinstimmt.
Mit modernen statistischen Verfahren können wir Zeitreihen wie die Veränderung des mittleren globalen Meeresspiegels (GMSL) valider und ausgefeilter vorhersagen als durch den einfachen Vergleich ausgewählter Anpassungen nach der Methode der kleinsten Quadrate, wie es das IPCC im AR6 tut. Unsere Vorhersage basiert auf reiner Statistik. Sie ist zwar korrekt, aber nicht unbedingt richtig, so sind Statistiken nun einmal. Wir werden es bis 2100 nicht mit Sicherheit wissen.
Abbildung 1 ist ein Diagramm der Daten, die wir verwenden werden – der NOAA-Meeresspiegel-Datensatz. Man kann erkennen, dass die Daten autokorreliert sind, was bedeutet, dass die Schätzung des mittleren Meeresspiegels in jedem Quartal stark vom Wert des vorangegangenen Quartals abhängt. Die Autokorrelation ist bei der Regression nach der Methode der kleinsten Quadrate zu berücksichtigen, insbesondere bei der Vorhersage von Zeitreihen, wird aber vom IPCC routinemäßig ignoriert.
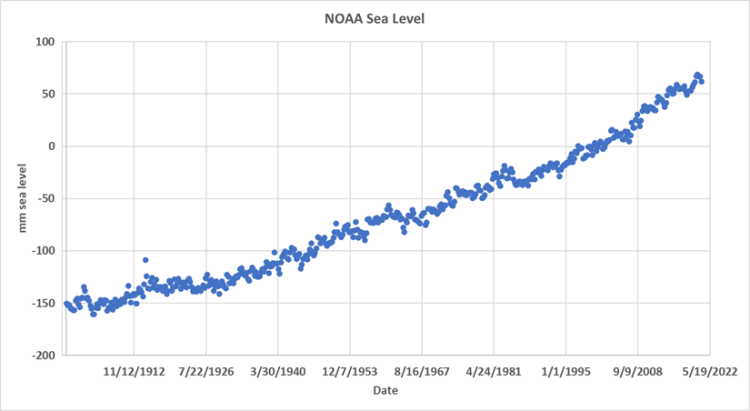
Abbildung 1. Mittlere NOAA-Meeresspiegelanomalie, 1900 bis 2022. Jeder Punkt steht für ein Quartal (3 Monate).
In Abbildung 2 wird jede Schätzung des Meeresspiegels gegen die vorherige Schätzung aufgetragen. Das R² der ersten Verzögerung beträgt 0,97, der Meeresspiegel ist also stark autokorreliert. Dies ist offensichtlich, bedeutet aber, dass die Statistik der kleinsten Quadrate für die lineare Anpassung ungültig ist, da die Statistiken der kleinsten Quadrate, wie R², davon ausgehen, dass die Fehler der Regression unabhängig sind. Die Methode der kleinsten Quadrate, wie sie im AR6 zur Darstellung der Beschleunigung verwendet wird, ist für einen Datensatz wie diesen ungeeignet. Der größte Teil eines beliebigen Wertes hängt stark vom vorherigen Wert ab. Das bedeutet, dass der mittlere quadratische Fehler (MSE) viel zu klein ist, wodurch der Fehler der Anpassung zu klein wird. Infolgedessen ist jede Kleinste-Quadrate-Linie der Daten in Abbildung 1 oder eines Teils dieser Daten statistisch nutzlos, es sei denn, die Autokorrelation wird berücksichtigt.
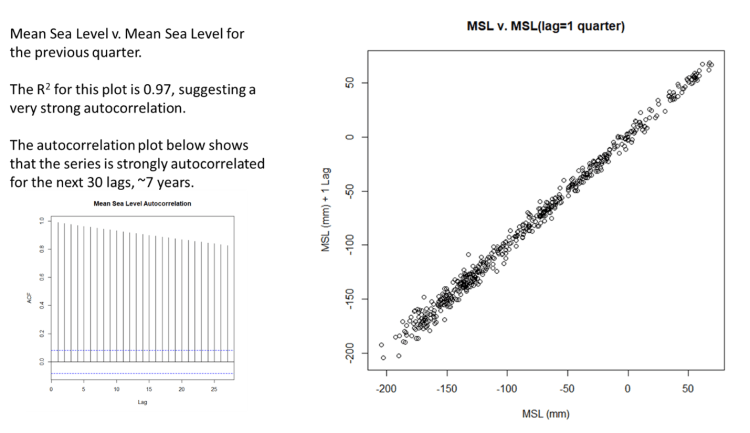
Abbildung 2. Aufzeichnung der GMSL gegen die vorherige GMSL, die erste Verzögerung. Die Werte sind stark korreliert. Die kleine Autokorrelationskurve zeigt, dass die GMSL seit mindestens 7 Jahren stark autokorreliert ist.
Wie können wir also GMSL auf statistisch gültige Weise vorhersagen? Wir können eindeutig nicht die kleinsten Quadrate verwenden und müssen fortgeschrittenere Techniken anwenden. Der erste Schritt besteht darin, die Autokorrelation aus den Daten zu entfernen. Dies geschieht in der Regel durch Subtraktion des vorherigen GMSL-Werts vom aktuellen Wert und dann auf diese Weise im gesamten Datensatz. Wir haben dies getan und zeigen eine Darstellung des Ergebnisses in Abbildung 3:
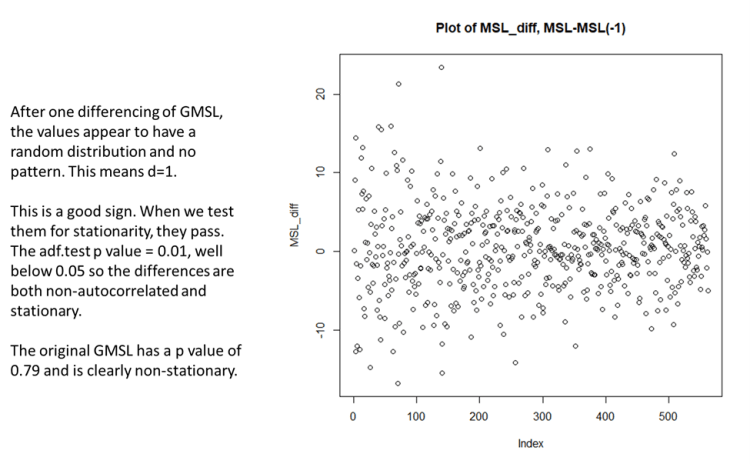
Abbildung 3 Eine Darstellung der ersten Differenz der GMSL. Die Darstellung ist zufällig und ziemlich gleichmäßig von links nach rechts, was darauf hindeutet, dass die Autokorrelation entfernt wurde und die Daten stationär sind.
Die Daten der ersten Differenz von GMSL sehen ziemlich gut aus, sehr ähnlich wie weißes Rauschen. Das ist genau das, was wir für eine valide statistische Analyse und Vorhersage brauchen. Wir werden eine R-Funktion namens „arima“ verwenden, um unsere GMSL-Prognose zu erstellen, und diese Funktion benötigt drei Parameter, um zu funktionieren, sie heißen p, d und q. Diese Parameter teilen arima mit, wie es die Eingabedaten konditionieren und ein Modell erstellen soll, das gültige zukünftige Werte projizieren kann. Das Diagramm in Abbildung 3 zeigt uns, das „d“ gleich eins ist. Das bedeutet, dass die Autokorrelation beseitigt wird, wenn man eine Differenz der benachbarten Werte nimmt. Außerdem müssen die Daten stationär sein, d. h. die statistischen Eigenschaften dürfen sich nicht mit der Zeit ändern (von links nach rechts). Der ursprüngliche Datensatz (Abbildung 1) war eindeutig nicht stationär, und das ist in Ordnung, wir wollen nur nicht, dass die Art und Weise, wie sich GMSL ändert, für diese Analyse eine Funktion der Zeit ist. Die R-Funktion Augmented Dickey-Fuller Test (ADF) bestätigt dies, da der ursprüngliche Datensatz einen ADF p-Wert von 0,79 aufweist, was bedeutet, dass er nicht stationär ist. Der arima p-Wert ist nicht dasselbe wie der statistische p-Test.
Die in Abbildung 3 dargestellten Differenzen haben einen ADF p-Wert von 0,01, also deutlich unter 0,05, dem Schwellenwert, der für den Nachweis der Stationarität erforderlich ist. Die Daten sind stationär, wenn die Verteilung über den untersuchten Zeitraum gleichmäßig um den Mittelwert verteilt ist. Das heißt, die Verteilung variiert nach oben und unten nicht signifikant mit der Zeitachse (x).
Als Nächstes müssen wir die arima p- und q-Werte ableiten. Dazu benötigen wir die ACF- (Autokorrelation) und PACF-Diagramme (partielle Autokorrelation), die in Abbildung 4 dargestellt sind:
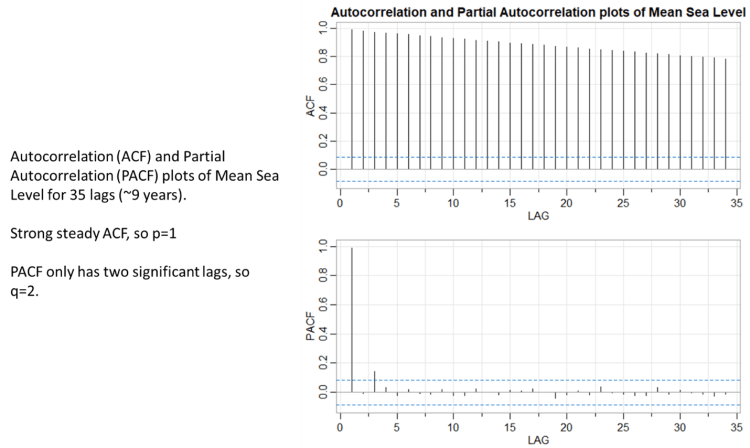
Abbildung 4. ACF– und PACF-Diagramme zur Bestimmung von p und q. Das obere Diagramm zeigt, dass jeder Wert von eins oder mehr für p möglich ist, da die Reihe bei allen Verzögerungen sehr stark autokorreliert ist. Das untere Diagramm zeigt, dass nach Entfernung der Autokorrelation auf der ersten Ebene nur zwei signifikante Autokorrelationen verbleiben (1 und 3), so dass q = 2 ist.
Die Analyse der GMSL-Zeitreihe ergibt einen Arima-Parametersatz von (1,1,2) für (p,d,q). Wir können auch eine R-Funktion namens auto.arima ausführen, um zu sehen, welche Parameter sie empfiehlt. Wir stellen fest, dass sie sich ebenfalls für (1,1,2) entscheidet. Dies ist eine gute Bestätigung dafür, dass unsere Parameterauswahl korrekt ist. In Abbildung 5 sind die Ergebnisse grafisch dargestellt.
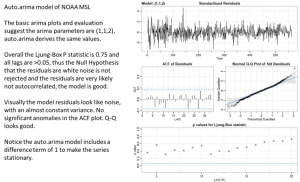
Abbildung 5. Die Ergebnisse eines Arima-Prognosemodells. Das obere Diagramm zeigt die Residuen, als nächstes sehen wir die ACF der Residuen und das Q-Q-Diagramm, beide sehen gut aus. Das untere Diagramm zeigt die Ljung-Box-Statistiken für verschiedene Lags und sie liegen alle über 0,05, was bedeutet, dass die Residuen weißes Rauschen sind, genau das, was wir wollen.
Aus Abbildung 5 geht hervor, dass das Modell die Trends des mittleren Meeresspiegels von 1880 bis 2020 im Wesentlichen korrekt wiedergibt. Die Modellresiduen zeigen keinen Trend und sind nicht autokorreliert. Abbildung 6 zeigt die Arima-Vorhersage aus dem (1,1,2)-Modell:

Abbildung 6. Die arima-Vorhersage des mittleren Meeresspiegels bis 2100. Die dargestellten Konfidenzgrenzen sind 95%-Grenzen. Links unten ist ein Histogramm der Modellresiduen dargestellt. Die Residuen sind erfreulicherweise normal.
Abbildung 7 ist ein Diagramm der Vorhersage aus Excel, das leichter zu lesen ist. Die von uns erstellte Vorhersage sagt voraus, dass der GMSL bis zum Jahr 2100 zwischen 148 und 258 mm steigen wird. Viele Forscher bezeichnen dies als alarmierend, aber die Menschen haben sich in der Vergangenheit erfolgreich an viel höhere Anstiegsraten des Meeresspiegels angepasst, wie wir in Abbildung 2 von Beitrag 1 sehen können, und zwar ohne die Technologie, die wir heute haben. Wenn wir bedenken, dass der durchschnittliche tägliche Tidenhub im offenen Ozean 1.000 mm beträgt, erscheinen 203 mm Meeresspiegelanstieg in 100 Jahren nicht viel. Im 20. Jahrhundert stieg der Meeresspiegel um 140 mm, hat das irgendjemand bemerkt oder interessiert, abgesehen von ein paar Forschern?
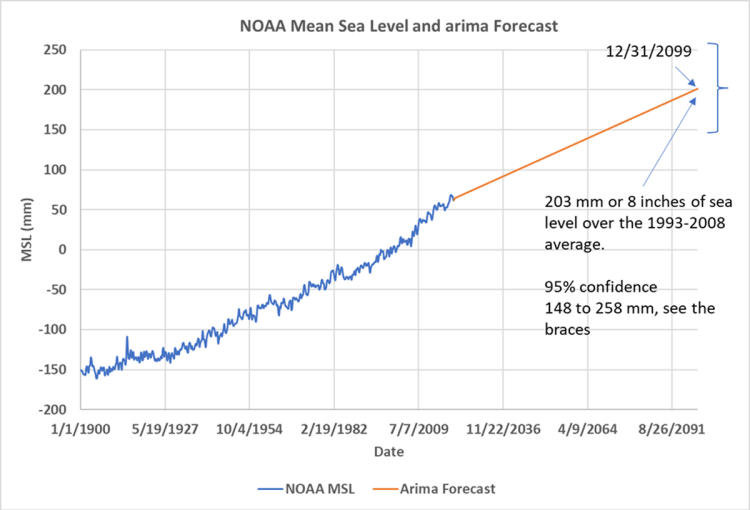
Abbildung 7. Die Vorhersage mit mehr Details. Das Modell sagt für das Jahr 2100 einen mittleren Meeresspiegel von 203 mm gegenüber dem Durchschnitt von 1993-2008 voraus. Die 95%-Konfidenzgrenzen liegen zwischen 148 mm und 258 mm und sind mit einer geschweiften Klammer gekennzeichnet. Die Spanne der Vorhersagen ist nicht alarmierend, sie liegt knapp über den 140 mm oder 5,5 Zoll, die im 20. Jahrhundert gemessen worden waren.
Schlussfolgerungen
In den Vereinigten Staaten würde man den Versuch des AR6, uns von einer Beschleunigung des Meeresspiegel-Anstiegs zu überzeugen, indem man nebeneinander liegende, herausgepickte Linien der kleinsten Quadrate verwendet, als „unausgereift“ bezeichnen. Ihre Methode ist problematisch, weil GMSL stark autokorreliert und nicht stationär ist, was ihre kirschgepickten Kleinstquadrat-Anpassungen und Kleinstquadrat-Statistiken ungültig macht.
Unsere Anpassung unter Verwendung der R-Funktion arima ist zumindest statistisch gültig. Wir haben speziell die Autokorrelation korrigiert und die Reihen zur Stationarität gezwungen. Wir haben auch die geringfügige partielle Autokorrelation korrigiert, die bei einem Viertel und drei Vierteln verblieben war. Die Residuen unseres Modells bestanden sowohl den allgemeinen Ljung-Box-Test als auch den Multiple-Lag-Ljung-Box-Test für weißes Rauschen, was bedeutet, dass das Arima-Modell den 140-jährigen Trend in den NOAA-Meeresspiegeldaten korrekt erfasst hat.
Während AR6 also nur bestimmte Zeiträume ausgewählt hat, um ihre Schlussfolgerung zu untermauern, dass sich der GMSL beschleunigt, sind wir unter Verwendung aller Daten auf statistisch gültige Weise zu der gegenteiligen Schlussfolgerung gelangt. Das bedeutet nicht, dass unsere Vorhersage richtig ist, aber es bedeutet, dass die Spekulation von AR6, der Meeresspiegel könnte bis 2150 um 5 Meter steigen, extrem unwahrscheinlich ist und am besten als unverantwortliche Spekulation bezeichnet werden sollte. Unsere Analyse ergab keine statistischen Hinweise auf eine Beschleunigung, sondern eine lineare Extrapolation.
[Hervorhebung vom Übersetzer]
Während die Erwärmung der Erdoberfläche eindeutig der Grund für das Abschmelzen der Gletscher auf dem Festland ist, was zum Anstieg des Meeresspiegels beiträgt, liefert der AR6 keinen Beweis dafür, dass die Erwärmung durch menschliche Aktivitäten verursacht wurde. Sie verwenden Modelle, um auf den Menschen als Verursacher zu schließen, aber leider sind auch ihre Modelle statistisch nicht valide, wie in Teil 2 sowie von McKitrick und Christy (McKitrick & Christy, 2018) gezeigt wird. Wir sind uns alle einig, dass der Mensch wahrscheinlich einen gewissen Einfluss auf die Erwärmung der Atmosphäre hat, aber wir wissen nicht, wie viel davon vom Menschen verursacht wurde und wie viel natürlich ist, weil wir gerade die ungewöhnlich kalte Kleine Eiszeit – die „vorindustrielle“ Periode – hinter uns haben. Wie wir in Teil 2 gesehen haben, zeigen die 30-Jahres-Raten des Meeresspiegelanstiegs eine deutlich natürlich aussehende Oszillation. Das Abschmelzen von Gletschereis und Eisschilden ist wahrscheinlich für den größten Teil des Meeresspiegelanstiegs verantwortlich, wie AR6 feststellt, aber der Anteil des Menschen an dieser Erwärmung könnte recht gering sein.
Aus rein statistischer Sicht sind die Behauptungen des AR6 also auf kindische Weise ungültig. Eine korrekte Analyse der Daten führt zu einer Vorhersage von etwa 20 cm Meeresspiegelanstieg bis zum Jahr 2100. Im Jahr 2100 werden unsere Nachkommen wissen, wer Recht hatte.
The data and R code to create the figures in this chapter can be downloaded here. The R code and spreadsheet provide much more detail about the arima forecast, including references not supplied below.
Reference
McKitrick, R., & Christy, J. (2018, July 6). A Test of the Tropical 200- to 300-hPa Warming Rate in Climate Models, Earth and Space Science. Earth and Space Science, 5(9), 529-536. Retrieved from https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2018EA000401
Übersetzt von Christian Freuer für das EIKE