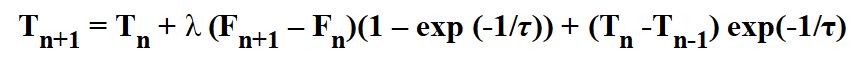Außerhalb der ‚Blackbox‘
Ad Huijser
Nach der Lektüre von „Into The Black Box“ (Ref. 1), wieder einmal ein großartiger und sehr informativer Beitrag von Willis Eschenbach, war ich nicht so sehr von der Schlussfolgerung überrascht, dass ein „Einzeiler-Klimamodell“ ein ähnliches Ergebnis wie die kompliziertesten GCMs erzielen könnte. Allerdings war ich verwundert darüber, dass er seine Analyse an dieser Stelle abbrach. Die von ihm angewandte wiederkehrende Beziehung zwischen Temperaturänderung und Antrieb ist eine einfache Folge davon, wie die Oberflächentemperatur T(t) dynamisch das Ungleichgewicht zwischen ein- und ausgehender Strahlung am TOA wiederherstellt, das durch einen zeitabhängigen Antrieb F(t) verursacht wird. Und da dies auf dem grundlegenden Prinzip der Energieerhaltung beruht, ist dies nicht nur ein weiteres 1-D-Klimamodell, sondern eine Voraussetzung für alle Klimamodelle. Er hätte sie also nicht nur zur Kurvenanpassung der Ergebnisse von GCMs verwenden sollen, sondern auch zur Überprüfung der Qualität von GCMs.
Schauen wir uns also diese wiederkehrende Beziehung, die ich (provokativ) als CMC bezeichne, etwas genauer an: den Climate Model Checker. Wenn n-1, n, n+1 aufeinanderfolgende Zeitpunkte in Einheitszeitintervallen sind, können wir diese Beziehung für kleine Störungen der Energiezu- und -abflüsse des Klimasystems der Erde leicht aus der Energiebilanz nach C ∂T/∂t = „Radiation IN“ – „Radiation OUT“ ableiten, als:
wobei τ eine spezifische Reaktionszeit ist, die in erster Linie durch die Wärmekapazität C des Klimasystems der Erde bestimmt wird, und λ ein Faktor, der die Klimasensitivität darstellt, d.h. die Art und Weise, wie die Oberflächentemperatur T auf ein Ungleichgewicht F an der TOA reagiert. Es ist offensichtlich, dass λ = ∆T/F ist, wobei ∆T der Anstieg der Oberflächentemperatur für t®µ aufgrund eines schrittweisen Antriebs F bei t = 0 ist. Diese Empfindlichkeit kann mit dem Temperaturanstieg aufgrund des Antriebs einer Verdopplung der CO2-Konzentration in Beziehung gesetzt werden, der bekannten Gleichgewichts-Klimaempfindlichkeit, ausgedrückt als ECS = λ F2xCO2.
Man könnte einwenden, dass ich das Problem auf die Schätzung der Parameter λ und τ und damit auf die laufende Diskussion „Welchen Wert hat ECS?“ verlagert habe. Das stimmt, aber erstens müssen wir jetzt nur noch zwei Parameter anpassen und nicht mehr den großen Satz von Parametern/Schätzungen in jedem komplizierten GCM. Und zweitens können wir zunächst nur das verwenden, was uns vernünftig erscheint, und dann sehen, was wir daraus machen.
Zunächst müssen wir einen realistischen Wert für τ schätzen. Für einen Wasserplaneten und je nach Wahl der Tiefe der gemischten Ozeanschicht kommen Lehrbücher (z. B. Ref. 2) auf etwa 4-5 Jahre. Bei 1/3 Land wird dieser Wert wahrscheinlich nicht viel niedriger als 3 Jahre sein. Ein Mittelwert von 4 Jahren ist eine gute Schätzung und wird durch Willis‘ Analyse von τ = 4,2 bei der Anpassung dieser CMC an das CMIP5-Ensemble (Ref. 1) unterstützt. In der Praxis zeigt sich, dass diese CMC nicht sehr empfindlich auf Reaktionszeiten im Intervall von 3 bis 5 Jahren reagiert.
Als Nächstes brauchen wir eine Schätzung für die Klimasensitivität λ. Für den Anfang wähle ich blind den Kehrwert des Planck-Rückkopplungsparameters von 3,3 W/m²/K (kümmern Sie sich hier nicht um Vorzeichen), da er aus demselben Ursprung wie unsere CMC abgeleitet ist und 4(1-a)Φ0/TS0 entspricht, wobei die Albedo des gesamten Himmels a = 0 ist. 3, der durchschnittlichen solaren Einstrahlung Φ0 = 340 W/m² und der Gleichgewichtsoberflächentemperatur TS0 = 288 K. λ = 0,3 K/ W/m² wäre also eine ausgezeichnete Wahl, und in der Tat zeigt Willis‘ Analyse (Ref. 1) der besten Anpassungen an die CMIP5-Ergebnisse Werte, die diesem Wert nahe kommen.
Aber diese Werte passten nicht gut zu den Berkeley-Temperaturreihen, für die er λ = 0,4 K/ W/m² und τ = 5 Jahre benötigte. Nun wissen wir alle, dass der Output von Modellen eine „Übersetzung“ des Inputs ist, oder kurz gesagt: „was man hineinsteckt, kommt heraus“ (aber nicht vergessen: „was man nicht hineinsteckt, kann man nicht herausbekommen“). Es stellt sich also die Frage, ob der Unterschied zwischen dem Berkeley- und dem von der CMC berechneten Temperaturbereich auf die falsche Wahl von λ und τ zurückzuführen ist oder eine Auswirkung des gewählten „Inputs“, d. h. der zeitabhängigen Antriebe ist.
Um das herauszufinden, habe ich Eschenbachs Excel-Tabelle heruntergeladen und meine eigene Tabelle entsprechend erstellt. Um meine Tabelle zu testen, habe ich dieselben CMIP5-Daten von der NASA/GISS-Website (Ref. 3) verwendet. Anstelle der Berkeley-Temperaturreihen verwendete ich zum Vergleich die neuesten HadCrut v5-Reihen (Ref. 4), die „aktueller“ sind. Schnell wurde klar, dass diese CMC mit λ = 0,3 K/W/m² und τ = 4 Jahren recht gut zu den HadCrut v5-Temperaturreihen passt. Und mit einer leichten Erhöhung auf λ = 0,345 K/W/m² passt sie sogar hervorragend. Dieser etwas höhere Wert für λ basiert nicht auf einer Kurvenanpassung, sondern stammt aus den Simulationen mit dem Online-Modul MODTRAN der Universität Chicago (Ref. 5) für die US-Standardatmosphäre + Wolken (Stratus/Strato CU) + Relative Luftfeuchtigkeit mit dem Wert 1 und „konstant“. Da dies nichts an den Schlussfolgerungen ändert und ich im weiteren Verlauf dieses Aufsatzes auch einige Ergebnisse von MODTRAN unter diesen besonderen Bedingungen verwenden werde, werde ich aus praktischen Gründen bzw. aus Gründen der Konsistenz von nun an diesen höheren λ-Wert verwenden.
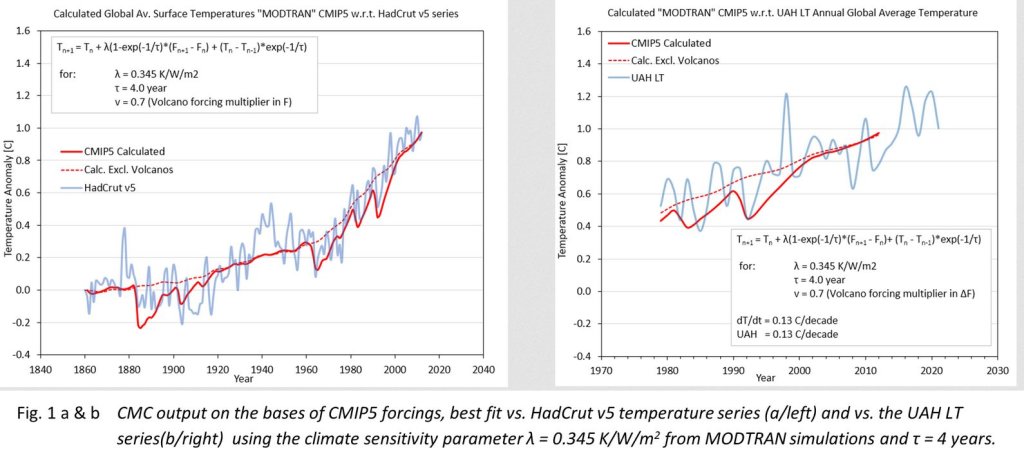
Diese Anpassung ist in Abb. 1a dargestellt, und in Abb. 1b ist die gleiche Anpassung mit der UAH-LT-Temperaturreihe (Ref. 11) gezeigt, die leider nur für die letzten 40 Jahre verfügbar ist. Um den Erwärmungstrend besser darzustellen, habe ich die Option genutzt, den Beitrag der Vulkane zum Gesamtantrieb zu unterdrücken (gestrichelte Linien).
Das ist natürlich nicht schlecht, aber keine Neuigkeit angesichts der früheren Analyse von Willis Eschenbach (siehe 1), und ich überlasse es anderen, die enormen Diskrepanzen zwischen dieser CMC und den gemessenen Temperaturen um 1940 (heiße Zeiten des Zweiten Weltkriegs?) zu erklären, die offenbar nicht auf bekannte anthropogene Einflüsse zurückzuführen sind.
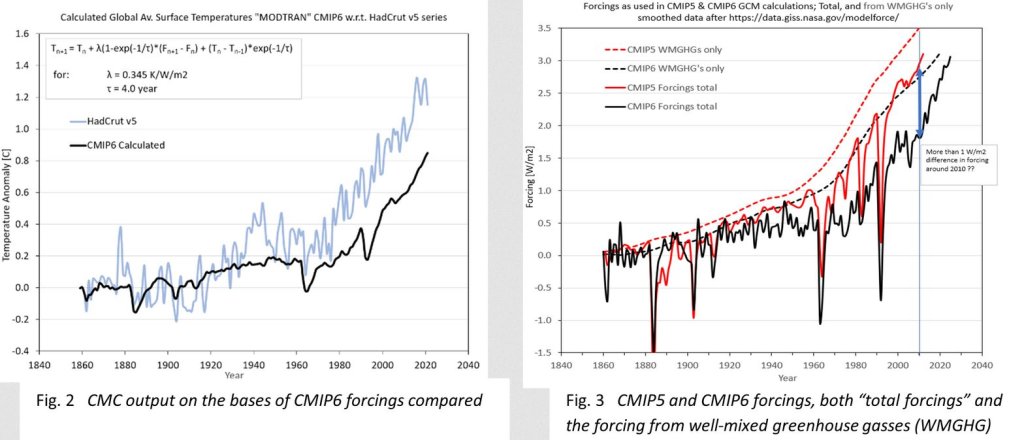
Beim Herunterladen der CMIP5-Forcings von der GISS-Website (Ref. 3) fiel mir jedoch auch die Verfügbarkeit der CMIP6-Datenbank auf. In der Erwartung, dass sie aktueller sein würde, habe ich auch diese Forcings ausprobiert (ich weiß nicht, warum Willis diesen Satz nicht verwendet hat). Jedenfalls war das Ergebnis der Anwendung dieser CMIP6-Inputs auf dieselbe CMC-Berechnung mit den identischen λ- und τ-Parametern eine völlige Überraschung, wie Abb. 2 zeigt. Und hier macht die Bemerkung, dass „der Output der Modelle immer ein Spiegelbild des Inputs ist“, deutlich, dass sich der Input der CMIP6-Modelle völlig von den CMIP5-Inputdaten unterscheidet, wie in Abb. 3 gezeigt. Und das nicht nur um einen kleinen Bruchteil; ein Forcing-Unterschied von 1 W/m² im Jahr 2010 bei einem Durchschnitt von 2,5 W/m² ist schlichtweg ungeheuerlich!
Man könnte einige neue Erkenntnisse in der Kategorie „natürliche Antriebe“ erwarten, aber nicht bei den Antrieben aus der Kategorie der gut gemischten Treibhausgase (WMGHG). Da beide Eingangsdaten von derselben Gruppe von Personen stammen, die auch die entsprechende Literatur (Ref. 6) zur Verfügung stellen, habe ich dort nach neuen Erkenntnissen oder guten Argumenten für diese Diskrepanzen gesucht. Sie wiesen auf einige Unterschiede hin, aber ohne klare Erklärungen. Vielleicht ist es mein Fehler, aber ich konnte keine ernsthafte Diskussion für ihre Entscheidungen finden. Wenn ich jedoch die folgende Erklärung auf ihrer Website lese (Ref. 3), habe ich den Eindruck, dass sie sich die Möglichkeit einräumen, alles anzupassen, was sie für notwendig halten, um den Input auf den Output abzustimmen:
„Die Quantifizierung des tatsächlichen Antriebs innerhalb eines globalen Klimamodells ist ziemlich kompliziert und kann vom Ausgangszustand des Klimas abhängen. Dies ist daher eine zusätzliche Quelle der Unsicherheit. In einem modernen, komplexen Klimamodell werden andere Antriebsfaktoren als die Sonnenenergie nicht als Energieflussstörung aufgezwungen. Vielmehr werden die Flussstörungen diagnostiziert, nachdem die spezifische physikalische Änderung vorgenommen wurde. Die aus einfacheren Modellen abgeleiteten Schätzungen für solare, vulkanische und gut gemischte Treibhausgase können sich von der Wirkung in einem GCM unterscheiden. Anstöße durch heterogenere Anstöße (Aerosole, Ozon, Landnutzung usw.) werden meist direkt aus den GCMs ermittelt“.
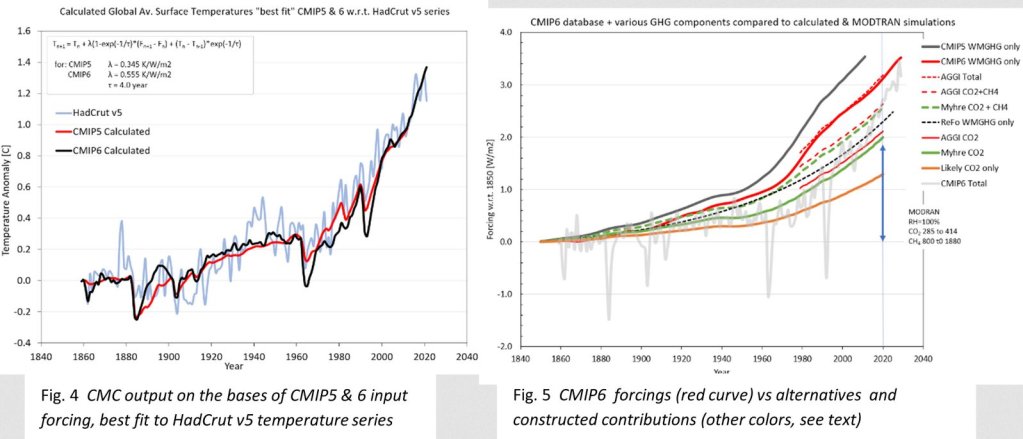
Das AGW-Narrativ des IPCC beruht zum Teil auf der Behauptung, dass all diese GCMs die Erwärmung seit der vorindustriellen Zeit angemessen wiedergeben können. Es ist nun klar, dass es bei solchen Behauptungen nicht um Klimamodelle geht, sondern um Modelle + Input. Während die CMIP5-Modelle+Input mit λ = 0,345 K/W/m² gut abgedeckt werden konnten, benötigen die CMIP6-Modelle+Input einen Wert von 0,555 K/W/m² (Abb. 4). Und offensichtlich sind diese „zusätzlichen“ 0,21 K/W/m² Klimasensitivität nicht modell-, sondern inputbezogen. Daher sind Diskussionen über die Veränderung der Klimasensitivität zwischen CMIP5- und CMIP6-Ensembles eigentlich nutzlos, solange Modelle und Input nicht eindeutig entkoppelt sind und die Modelle nicht mit demselben Satz von Treibhausgasen als Input verglichen werden. Es ist zu einfach, darüber zu spekulieren, dass dies ein Beweis für einen „abgestimmten“ Input ist, aber dieses Thema erfordert auf jeden Fall einen besseren Einblick in die in diesen Ensembles verwendeten Antriebe. Daher habe ich versucht, die CMIP6-Zusammensetzung genauer zu verstehen, da sie den geringsten WMGHG-Anteil aufweist, wie in Abb. 3 und 5 dargestellt.
In der herunterladbaren CMIP6-Datenbank sind alle Treibhausgase zu einem WMGHG-Forcing zusammengefasst, und um dieses zu zerlegen, habe ich AGGI verwendet, die NOAA Annual Greenhouse Gas Index-Daten (Ref. 7), die bis 1979 zurückreichen (dünne/rote Kurven in Abb. 5). Deren WMGHG-Gesamtmenge (rote gepunktete Linie) passt gut zu den CMIP6-Daten, aber überhaupt nicht zu den CMIP5-Daten (schwarze Linie). Es gibt vier Hauptverursacher: CO2 (durchgezogenes dünnes Rot), CH4 (zusätzlich zu CO2, gestricheltes dünnes Rot) und der „Rest“ aus NO2 und FCKW/HFCKW. Der steile Anstieg des Treibhauseffekts nach 1970 ist offensichtlich auf die beiden letztgenannten Komponenten zurückzuführen, aber es ist schwer vorstellbar, dass sie plötzlich mit etwa 1 W/m² zum gesamten Treibhauseffekt beitragen. Nichtsdestotrotz stimmen die CMIP6-Forcings mit diesen AGGI-Daten über den verfügbaren Zeitraum überein, so dass es sich wahrscheinlich um „objektive“ Bewertungen von Änderungen der THG-Konzentration in der Atmosphäre handelt.
Was wir in diesem Zusammenhang leicht überprüfen können, ist der Beitrag von Kohlendioxid und Methan. Hier ist das MODTRAN-Modul ein praktisches Werkzeug, da es die Rekonstruktion der Treibhausgase für CO2, das den größten Beitrag leistet, und Methan (CH4) als „Zweitplatzierten“ ermöglicht. Dazu benötigen wir lediglich die Konzentration dieser Treibhausgase seit der vorindustriellen Zeit. Für CO2 ist das kein Problem, denn wir haben die Mauna Loa-Daten und das Carbon Project mit langjährigen „besten Schätzungen“ für die historischen Emissionen fossiler Brennstoffe, und die rekonstruierten 280 ppm im Jahr 1850 scheinen unumstritten zu sein. Für Methan ist die Geschichte weniger klar. Wir haben seit 1984 zuverlässige Messungen, aber die Methanquellen sind ziemlich spekulativ, vor allem in Verbindung mit dem Wachstum der Weltbevölkerung und dem damit verbundenen Wachstum der Landwirtschaft und der Viehbestände. Die vorindustrielle Konzentration (etwa 800 ppb im Jahr 1850) stammt aus der Analyse der in Eisbohrkernen eingeschlossenen Luft. Wie zuverlässig diese Daten sind, ist fraglich. Obwohl ich die bekannten Konzentrationen auf etwa 1100 ppb im Jahr 1850 zurückgerechnet habe, indem ich die aktuellen Emissionsraten und eine Lebensdauer von 9 Jahren zugrunde gelegt habe, sehe ich keinen Grund, diesen „offiziellen“ Wert von 800 ppb zu verwerfen und ihn zur Berechnung des CH4-Antriebs zu verwenden. Wenn wir MODTRAN verwenden, um die Auswirkungen des Übergangs von den CO2– und CH4-Konzentrationen von 1850 auf die heutigen Werte (414 ppm bzw. 1880 ppb) zu simulieren, erhalten wir einen Gesamtenergieanstieg von 1,85 W/m² für die US-Standardatmosphäre mit Stratus/Stratocumulus-Wolken und einer Wasserdampfeinstellung von 1 bei konstanter Luftfeuchtigkeit. Letzteres simuliert die „Wasserdampf-Rückkopplung“ (WVFB), also die Auswirkung einer veränderten H2O-Konzentration aufgrund von Temperaturänderungen, so dass sich eine Diskussion über dieses kontroverse Thema erübrigt.
Dieser Gesamt-„MODTRAN“-CO2+CH4-Antrieb, der in Abb. 5 durch den blauen Pfeil gekennzeichnet ist, stellt sofort die Glaubwürdigkeit der NASA/GISS-Antriebe in Frage, die in den Datenbanken CMIP5 und CMIP6 verwendet werden. Die in der AGGI-Datenbank verwendeten Forcings scheinen auf der Arbeit von Myhre et al. (Ref. 8) zu beruhen, aus der wir sofort die Verwendung des bekannten 2xCO2-Forcings von 3,7 W/m² und CH4-Forcings aus derselben Studie erkennen (grüne durchgezogene und gestrichelte Kurven). Aus der neueren Arbeit von Van Wijngaarden und Happer (Ref. 9) wissen wir jedoch, dass der spezifische CO2-Antrieb sicherlich zu hoch ist und maximal 3,0 W/m² beträgt, da sie ihn nur für klare Himmelsbedingungen ermittelt haben. Das MODTRAN-Modul ergibt für diese Situation F2xCO2 = 2,95 W/m², was eine gute Übereinstimmung mit ihrer Arbeit darstellt. Für den gesamten Himmel (bewölkt), wie er in dieser Arbeit verwendet wird (einschließlich WVFB), sinkt dieser Wert sogar auf 2,26-2,36 W/m² (abhängig von der relativen Luftfeuchtigkeit zwischen 100-60%), da Wolken die Wirkung von Treibhausgasen teilweise abschirmen. Um in Abb. 5 den Unterschied zu verdeutlichen, habe ich die Kurve „nur CO2“ mit 2,4 W/m² (orangefarbene Kurve) eingefügt.
Der NO2-Beitrag im AGGI beträgt nicht mehr als 0,2 W/m², so dass der steile Anstieg der Treibhausgase auf die Chlorfluorkohlenstoffe zurückzuführen sein muss. In MODTRAN werden diese durch die Freon-Skala dargestellt, und wenn man diese zwischen 0 und 1 umschaltet, erhält man nur 0,09 W/m² an zusätzlichem Antrieb für diese Gase. Dieser niedrige Wert lässt sich nur schwer mit den etwa 0,5 W/m² Antrieben in Einklang bringen, die von den CMIP6- und AGGI-Daten angegeben werden.
Wie auch immer, die Gesamtdifferenz des WMGHG’s CO2 + CH4 + NO2 + FCKW’s zwischen 2020 und 1850 wird sicherlich nicht mehr als 2,3 W/m² nach den obigen Zahlen betragen; wesentlich niedriger als die 3,2 W/m², die in der CMIP6-Datenbank von NASA/GISS verwendet werden. Und ich sehe absolut keinen Grund, an meiner Rechnung zu zweifeln, und sehe auch keine Möglichkeit, diese Lücke von fast 1 W/m² zu schließen.
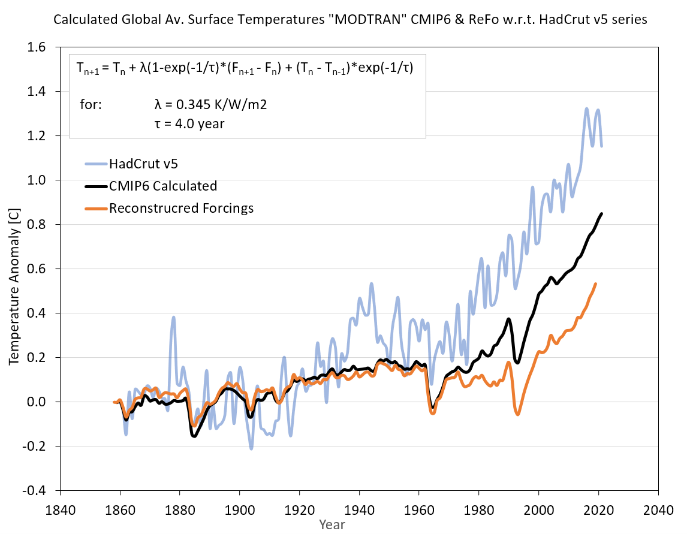
Abb. 6 Der Temperatureffekt bei Anwendung von CMC mit den REFO-Gesamtforcings, wie sie u.a. aus dem „natürlichen“ Teil von CMIP6 und den MODTRAN-Werten (siehe Text) rekonstruiert wurden, im Vergleich zu HadCrut v5 und den Temperaturanomalien aufgrund der CMIP6-Gesamtforcings.
Natürlich könnten wir versuchen, diese Diskrepanz durch eine Anpassung der Klimasensitivität λ und/oder der Reaktionszeit τ zu beheben, aber das macht nicht viel Sinn, da wir mindestens 1 K/W/m² erreichen müssen. Dies würde eine lächerlich hohe Klimasensitivität bedeuten (nach ECS = λ F2xCO2 ≈ 3 K), obwohl sie immer noch innerhalb des IPCC-Bereichs liegt, oder, in der Terminologie der GCMs, ein Hinweis auf absurd hohe Rückkopplungen. Letzteres ist genau die Ausrede der CMIP6-Modelle und der Hintergrund für die jüngsten CMIP6-basierten alarmistischen Schlussfolgerungen einer noch höheren zukünftigen Erwärmung als bisher prognostiziert. Und was ich hier mit dieser CMC-Berechnung sowohl für den CMIP6- als auch für den REFO-Satz zeige ist, dass, wo die CMIP5-Modelle + Input anscheinend die gemessenen Temperaturreihen zwischen 1850-2020 einigermaßen gut anpassen können, die CMIP5- und 6-Modelle + objektiver Input (wie dieser REFO) überhaupt nicht passen.
Diese Lücke zwischen den aus den Antriebsfaktoren berechneten Anomalien und den Beobachtungen wird also nur schwer durch anthropogene Effekte zu schließen sein. Meine eigene Einschätzung (Ref. 10) ist, dass die Veränderung der Wolkenbedeckung seit 1980 diese Aufgabe übernehmen kann, wenn man eine Klimasensitivität gegenüber Wolkenveränderungen von etwa -0,11 K/%cc annimmt und nicht die unangenehm hohen positiven Wolkenrückkopplungen durch den Temperaturanstieg in den GCMs. Es ist erstaunlich, dass MODTRAN, im Gegensatz zu den GCMs, eine ähnliche Antwort auf diese Frage gibt, aber das ist eine „andere Geschichte“, die in diesem Zusammenhang nicht behandelt werden soll. Aber bedenken Sie, dass die beobachtete Wolkenveränderung möglicherweise nicht der einzige Effekt ist, der den globalen Klimawandel beeinflusst, so dass wir auch für andere Möglichkeiten offen bleiben müssen.
Abschließend möchte ich feststellen: Ich habe versucht, auf transparente Weise die Qualität der GCM-Klimamodelle zu analysieren und zu prüfen, ob die AGW-Hypothese durch diese Modelle für den Zeitraum 1850-2020 gut belegt ist, wie es das IPCC behauptet.
Nach dieser Untersuchung kann ich nur sagen: „Nein, absolut nicht!“. Modelle, die Modell-spezifische Eingaben benötigen, um die bekannte Vergangenheit zu replizieren, verletzen die grundlegendsten Kriterien der Wissenschaft, um das Etikett „wissenschaftlich bewiesen“ zu verdienen, unabhängig von der „bewiesenen Physik“, auf der sie beruhen. Diese Modelle sind in der Tat „Black Boxes“, aber ohne jede Vorhersagbarkeit. Die eklatanten Ungereimtheiten bei den Eingabewerten zwischen den verschiedenen Generationen sollten bereits Grund genug sein, jedes Ergebnis abzulehnen. Folglich sind diese Modelle in jeder Hinsicht völlig ungeeignet, die Zukunft vorherzusagen.
Die Frage: „Sind diese CMIP5- und CMIP6-Forcings auf die Temperaturen der letzten 1½ Jahrhunderte fixiert, um den jeweiligen GMC-Modellen ein vorbestimmtes/wünschenswertes Ergebnis zu geben?“, bleibt unbeantwortet, da ich keinen Einblick in die tatsächliche Abstimmung der GMCs habe. Aber diese Analyse in Verbindung mit dem früheren Zitat von der NASA/GISS-Website lässt diese Möglichkeit eindeutig offen.
Diese Schlussfolgerung macht mich nicht zu einem Klimaleugner oder einem Befürworter der weiteren Umweltverschmutzung, aber die Idee, dass die globale Erwärmung durch massive CO2-Reduktionen beeinflusst, wenn nicht gar gestoppt werden könnte, wird meiner Meinung nach nicht durch angemessene wissenschaftliche Beweise gestützt.
Mit Dank an Willis Eschenbach, der mich zu dieser Analyse veranlasst hat.
References
- Eschenbach, https://wattsupwiththat.com/2022/02/03/into-the-black-box/
- See for instance: http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2015/Notes/Lectures/Lecture02%20–%20Solving%20the%20zero-dimensional%20EBM.html
- https://data.giss.nasa.gov/modelforce/
- https://www.metoffice.gov.uk/hadobs/hadcrut5/
- http://climatemodels.uchicago.edu/modtran/
- Miller et al, 2014, CMIP5 historical simulations (1850-2012) with GISS ModelE2, Journal of Advances in Modeling Earth Systems, vol. 2, 441-468 https://doi.org/10.1002/2013MS000266 and
Miller et al, 2021, CMIP6 historical simulations (1850-2014) with GISS-E2.1, Journal of Advances in Modeling Earth Systems, vol. 13
https://doi.org/10.1029/2019MS002034 - https://gml.noaa.gov/aggi/aggi.html
- Myhre et al, 1998, New Estimates of Radiative Forcing due to Well Mixed Greenhouse Gasses, Geophysical Research Letters, vol 24, 2715-2718
- W.A. van Wijngaarden and W. Happer, Relative Potency of Greenhouse Molecules, arXiv:2103.16465v1, 30 Mar 2021
- Huijser, The under estimated role of Clouds, https://www.clepair.net/clouds-AdHuijser.pdf
- https://www.nsstc.uah.edu/data/msu/v6.0/tlt/uahncdc_lt_6.0.txt
Link: https://wattsupwiththat.com/2022/02/21/outside-the-black-box/
Übersetzt von Christian Freuer für das EIKE