Ein linearer Exkurs
In meinem vorigen Beitrag mit dem Titel [übersetzt] „Wo ist die Obergrenze der Atmosphäre?“ [in deutscher Übersetzung hier] habe ich die so genannte „Ordinary Least Squares“ (OLS) lineare Regression verwendet. Dies ist die Standardmethode der linearen Regression, die den Trend einer Variablen angibt. Hier ist zum Beispiel der Trend der linearen OLS-Regression der CERES-Oberflächentemperatur von März 2000 bis Februar 2021:
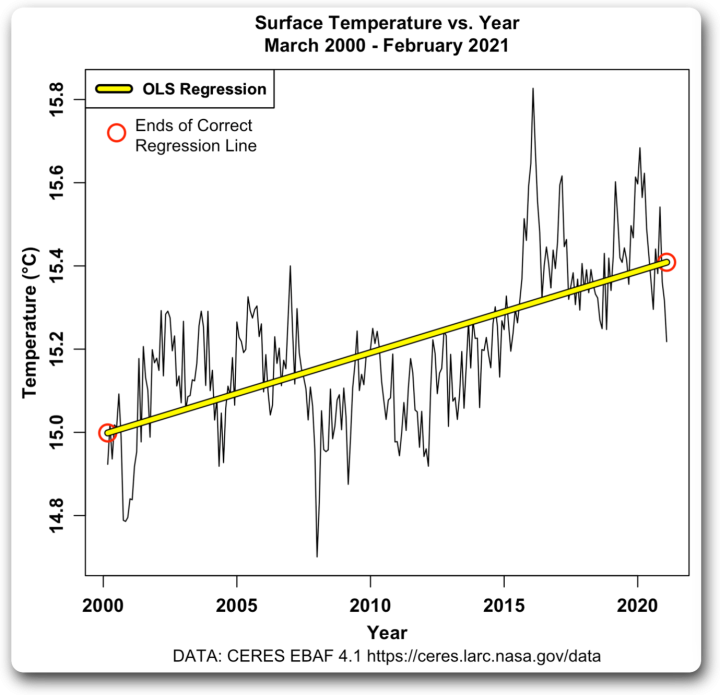
Abbildung 1. OLS-Regression, Temperatur (vertikale oder „Y“-Achse) gegen Zeit (horizontale oder „X“-Achse). Die roten Kreise markieren die Enden der korrekten Regressionstrendlinie.
Es gibt jedoch eine wichtige Einschränkung bei der linearen OLS-Regression, die mir nicht bekannt war. Dank eines statistisch versierten Kommentators zu meinem letzten Beitrag habe ich herausgefunden, dass bei der Verwendung der linearen OLS-Regression immer etwas beachtet werden muss:
Sie liefert nur dann die richtige Antwort, wenn die Daten auf der X-Achse keine Fehler aufweisen.
Wenn Sie eine Variable auf der Y-Achse gegen die Zeit auf der X-Achse betrachten, ist das kein Problem. Obwohl die Werte einer Variablen wie der in Abbildung 1 dargestellten globalen Durchschnittstemperatur in der Regel mit einer gewissen Unsicherheit behaftet sind, kennen wir den Zeitpunkt der Beobachtungen im Allgemeinen recht genau.
Nehmen wir jedoch an, wir verwenden genau dieselben Daten, setzen die Zeit auf die Y-Achse und die Temperatur auf die X-Achse und verwenden eine OLS-Regression, um den Trend zu ermitteln, bekommen wir das hier:
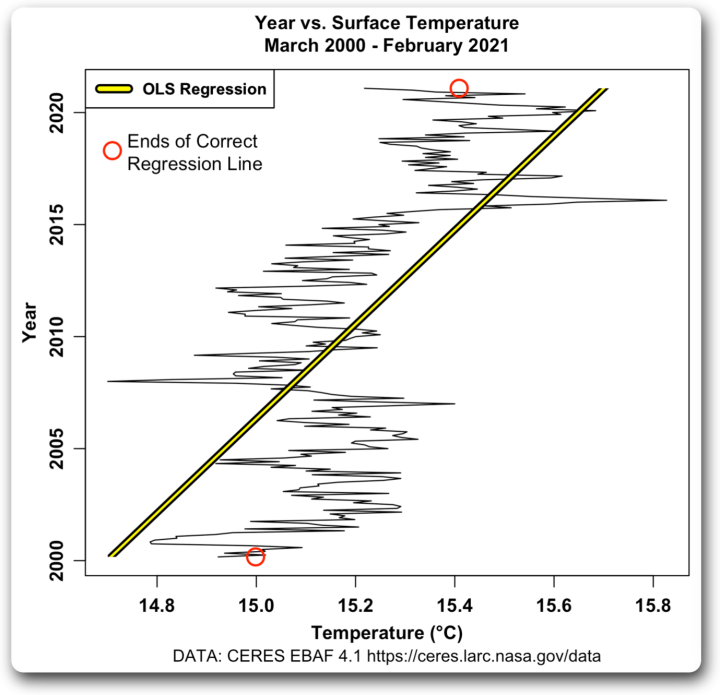
Abbildung 2. OLS-Regression, Zeit (vertikale oder „Y“-Achse) gegen Temperatur (horizontale oder „X“-Achse). Wie in Abbildung 1 markieren die roten Kreise die Enden der korrekten Regressionstrendlinie.
HILFE! Das ist ganz, ganz falsch. Sie unterschätzt Der wahren Trend wird erheblich unterschätzt.
Glücklicherweise gibt es eine Lösung. Sie heißt „Deming-Regression“ und setzt voraus, dass Sie die Fehler in den Variablen der X- und Y-Achse kennen. In Abbildung 2 ist die Deming-Regressions-Trendlinie in rot dargestellt:
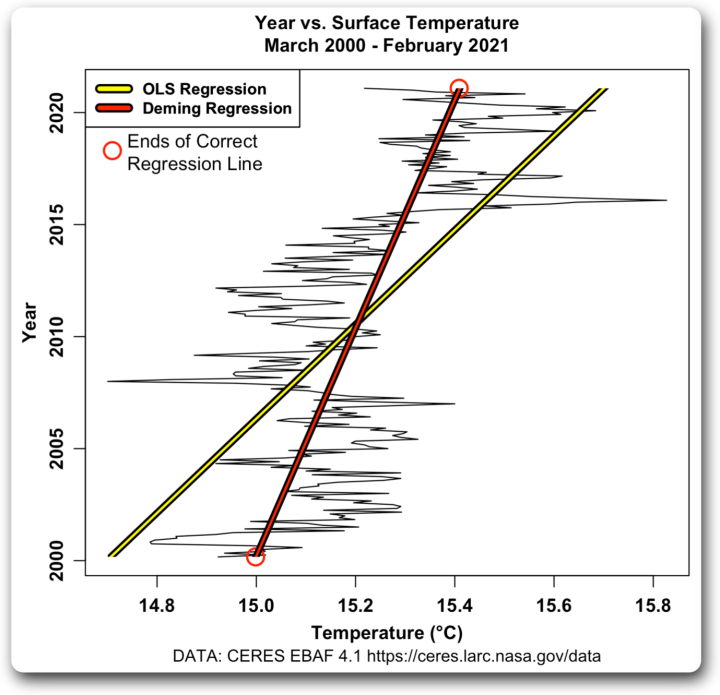
Abbildung 3. OLS- und Deming-Regression, Zeit (vertikale oder „Y“-Achse) gegen Temperatur (horizontale oder „X“-Achse). Wie in Abbildung 1 markieren die roten Kreise die Enden der korrekten Regressions-Trendlinie.
Wie man sieht, liefert die Deming-Regression die richtige Antwort.
Und das kann sehr wichtig sein. In meinem letzten Beitrag habe ich zum Beispiel die OLS-Regression in einem Streudiagramm verwendet, in dem ich die aufsteigende Langwellen-Strahlung (Y-Achse) über der Atmosphäre (TOA) mit der Oberflächentemperatur (X-Achse) verglichen habe. Das Problem besteht darin, dass sowohl die TOA-Aufstiegs-LW als auch die Temperaturdaten Fehler enthalten. Hier ist das Diagramm:
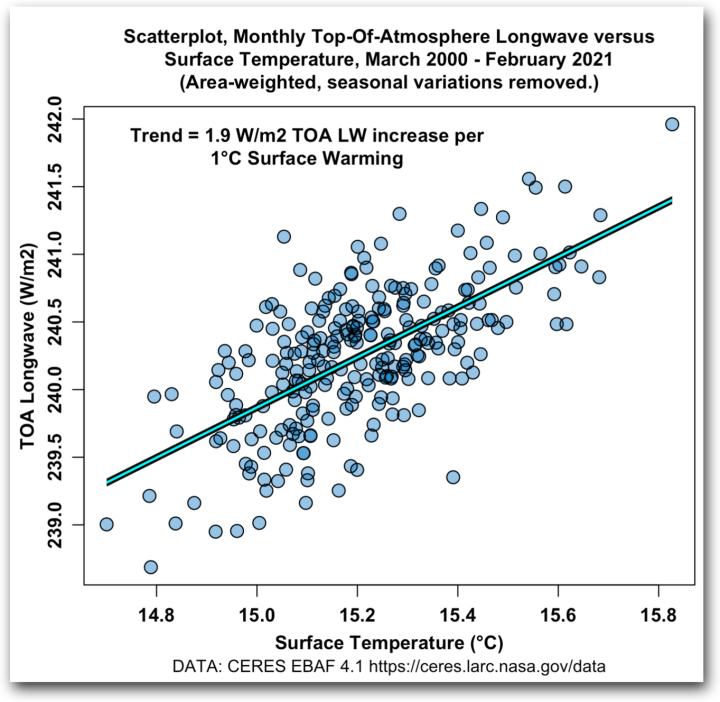
Abbildung 4. Streudiagramm, monatliche aufsteigende Langwellen-Strahlung an der Obergrenze der Atmosphäre (TOA LW) gegen Oberflächentemperatur. Die blaue Linie ist die falsche OLS-Regressions-Trendlinie.
Sie ist aber wegen des Fehlers auf der X-Achse nicht korrekt. Nachdem der Kommentator auf das Problem hingewiesen hatte, habe ich sie durch die korrekte Deming-Regressions-Trendlinie ersetzt:
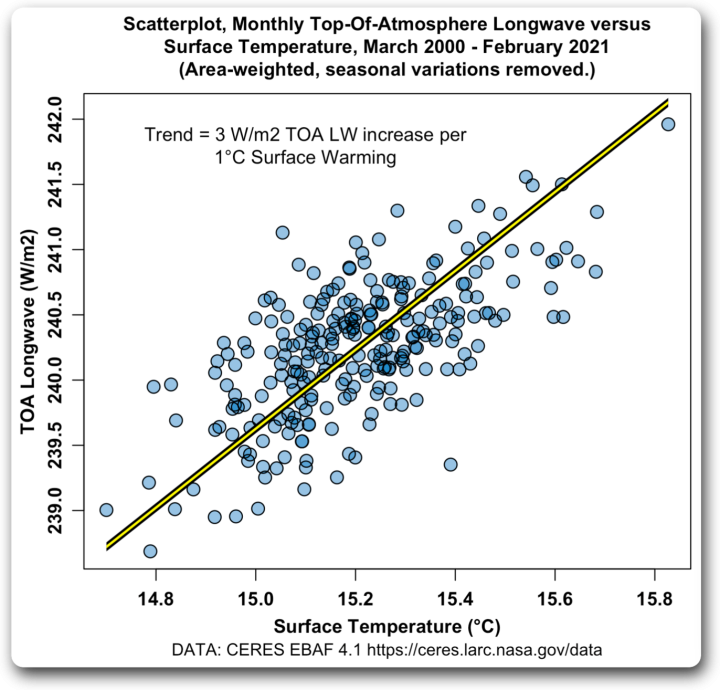
Abbildung 5. Streudiagramm, monatliche aufsteigende Langwellen-Strahlung oberhalb der Atmosphäre (TOA LW) gegen Oberflächentemperatur. Die gelbe Linie ist die korrekte Deming-Regressions-Trendlinie.
Und das ist ziemlich wichtig. Unter Verwendung des falschen Trends, der durch die blaue Linie in Abbildung 4 dargestellt wird, habe ich die Gleichgewichts-Klimasensitivität fälschlicherweise mit 1°C für eine Verdoppelung des CO2 berechnet.
Mit dem korrekten Trend, der durch die blaue Linie in Abbildung 5 dargestellt wird, berechne ich die Gleichgewichts-Klimaempfindlichkeit als 0,6 °C für eine Verdoppelung des CO2 … ein signifikanter Unterschied.
Ich liebe es, für das Internet zu schreiben. Egal, über welches Thema ich schreibe, ich kann garantieren, dass meine Beiträge von Leuten gelesen werden, die viel mehr über das betreffende Thema wissen als ich … und so lerne ich ständig Neues dazu. Das ist die beste Peer-Review der Welt.
Aktualisierung
Ein befreundeter Kommentator machte darauf aufmerksam:
Zunächst einmal ist der CERES-Datensatz viel zu kurz, um eine ECS abzuschätzen.
Ich habe geantwortet, dass die Klimasensitivität von der Vorstellung abhängt, dass die Temperatur steigen muss, um den Verlust an aufsteigender TOA-LW auszugleichen. Was ich getan habe, ist die Beziehung zwischen Temperatur und TOA-LW zu messen. Ich bat ihn, den Beweis zu erbringen, dass sich diese Beziehung im Laufe der Zeit verändert hat … denn wenn das nicht der Fall ist, warum sollte uns dann ein längerer Datensatz helfen?
Da musste ich natürlich einen Blick auf einen längeren Datensatz werfen. Die NOAA verfügt über Aufzeichnungen der aufsteigenden langwelligen TOA-Werte seit 1979, und Berkeley Earth verfügt über globale, gerasterte Temperaturen seit 1850. Also habe ich mir den Zeitraum angesehen, in dem sich die beiden Daten überschneiden, also von Januar 1979 bis Dezember 2020. Hier ist das Diagramm:
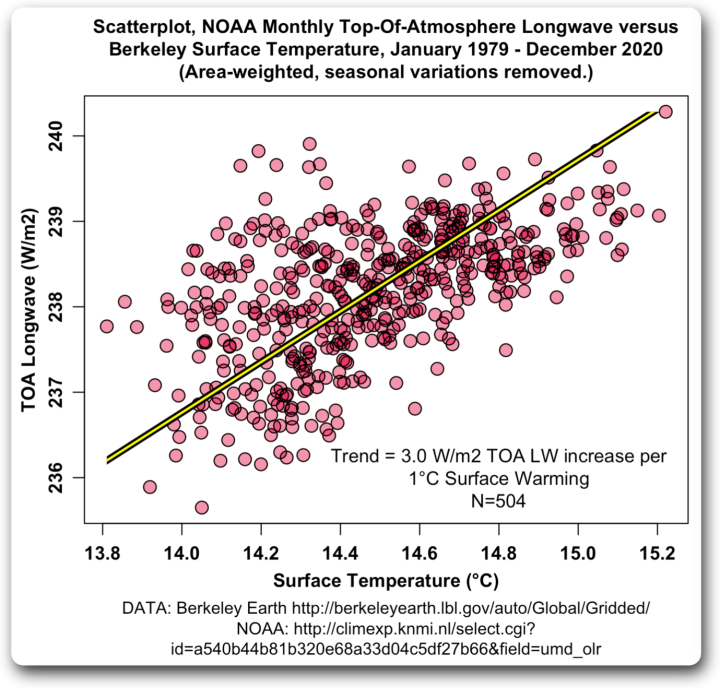
Abbildung 6. Streudiagramm, NOAA monatliche aufsteigende Langwellen-Strahlung über der Atmosphäre (TOA LW) gegen Berkeley Erdoberflächentemperatur. Die gelbe Linie ist die korrekte Deming-Regressions-Trendlinie.
Anstatt CERES-Daten für die Grafik zu verwenden, habe ich zwei völlig unterschiedliche Datensätze verwendet: die aufsteigende TOA-Langwelle von NOAA und die globalen, gerasterten Temperaturdaten von Berkeley Earth. Und trotzdem erhalte ich auf ein Zehntel Watt pro Quadratmeter genau dasselbe Ergebnis – 3,0 W/m² pro °C.
Link: https://wattsupwiththat.com/2022/01/09/a-linear-digression/
Übersetzt von Christian Freuer für das EIKE