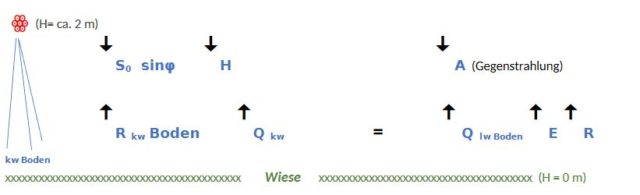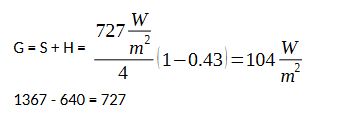Kritische Betrachtung der Gegenstrahlung, ihre Messung und ihre Bedeutung in der Treibhaushypothese der aktuellen Klimawissenschaft
Die Modellierung von Kiehl und Trenberth 1997 wirft aber auch zahlreiche Fragen auf. Es gibt doch deutliche Abweichungen zwischen den Satelliten Messwerten und dem vom Modell KT97 errechneten Werten. Diesen versuchten Trenberth, Fasullo und Kiehl 2009 1 entgegenzutreten. Hierbei wurde 2009 gleichzeitig der hypothetische Rechenwert der Gegenstrahlung auf 333 W/m² angehoben. Letzte Zweifel an ihrem Satellitenabgleich blieben wohl aber auch 2012 für Norman Loeb (NASA) bei seinem weltweiten Vergleich von 14 Instituten eingesetzten 22 CMIP5-/IPCC AR5 Klimamodellen bestehen. Norman Loeb schrieb: „In the present study, we do not only rely on satellite observations, but make extensive use of the information contained in radiation measurements taken from the Earth surface, to provide direct observational constraints also for the surface fluxes.” 2 Es wurde mit Pyranometer und Pyrheliometer gemessen. “…and the diffuse shortwave flux (measured with a shaded pyranometer). A pyranometer measures the total incoming solar radiation in the wavelengths between 0.3 and 2.8 µm. Datasets from both measurement methods are used in this study.” Die Gegenstrahlung der neuen CMIP5-Modellgeneration beträgt 2012 342 W/m² 4 im Gegensatz zu 324 W/m² bei KT97.
Es ist deshalb erforderlich, die Technik der Messung der Gegenstrahlung dieser Geräte genauer zu betrachten. Der nun folgende Teil entstammt Kapitel 4.24 „Die Strahlungsmessung der Gegenstrahlung“ aus, Agerius, 2021, Kritischer Analyse zur globalen Klimatheorie – Erweiterung, Vertiefung, Prognose, 2. überarbeitete Auflage, Hamburg, ISBN 978-3-347-24749-9. 16
Bevor man diese Messgeräte genauer betrachtet, die die Gegenstrahlung aus einem Algorithmus errechnen, müssen die Wellenlängen des Sonnenlichts, ihre Strahlenflussdichte und ihr Anteil an der Gesamtstrahlung hierzu betrachtet werden. Sie fließen in den Algorithmus ein.
Für einen mittleren Erdabstand von 1496 106 m und einer Solarkonstante von 1367 W/m² gilt:
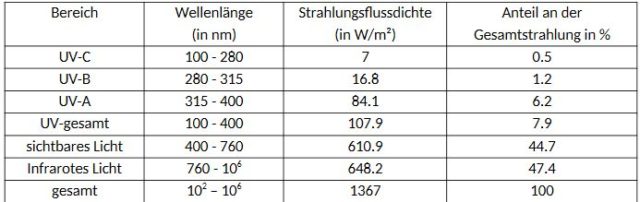
Tabelle 6 Spektralverteilung der extraterrestrischen solaren Strahlung, gemäß der World Meteorological Organisation, WMO, 1986 3
Die Gegenstrahlung (Back Radiation) wird auch gelegentlich auch als thermische Wärmestrahlung bezeichnet. Sie wäre bezüglich ihrer Wellenlänge langwellig. Verschiedene Messinstrumente zur Messung von lang- und kurzwelliger Strahlung wie Pyranometer (Messung der kurzwelligen Strahlung von Sonne, Himmel und der vom Erdboden reflektierten Strahlung), Infrarot-Pyranometer (Messung von langwelliger Strahlung), Pyrheliometer, Pyrradiometer und Pyrgeometer4 wurden entwickelt. Ihre Bezeichnungen lehnen sich an den Göttinger Katalog didaktischer Modelle an.5 Diese Messinstrumente arbeiten mit folgenden physikalischen Grundlagen.
Die solare Einstrahlung, Total Solar Irradiance (TSI) beträgt 1367 W/m². Die kurzwellige Strahlung der Sonne unterteilt sich in a) aus einem Anteil Sonnenstrahlung S = So sin φsonne mit φsonne, dem Winkel der Sonnenhöhe in Abhängigkeit vom Breitengrad, b) diffuse Himmelsstrahlung H aus der Streuung durch die Moleküle der Atmosphäre und c) kurzwellige Reflexstrahlung der Erdoberfläche Rkw. Hierbei ist εkw der mittlere Absorptionskoeffizient im kurzwelligen Bereich des Spektrums und a = (1-εkw) der hierzu gehörige Albedowert. S und H entstehen gemeinsam aus der Globalstrahlung G und mit Qkw, die den Saldo der kurzwelligen Strahlungsbilanz erfasst. Im Ausdruck G ist φsonne bereits berücksichtigt.
Nach KT97 im Mittel mit einer durchschnittlichen Global Mean Albedo ist a = 0.3129 und hierbei entsprechen die Pfeile analog der Richtung der Strahlung. Als Gleichgewicht an der obersten Atmosphärenschicht ergibt sich:
Übertragen für den Algorithmus der Messgeräte zur Gegenstrahlung A, aber als Gleichgewicht im Bereich des Aufstellungsortes des Messgerätes in Bodennähe: Hierbei befindet sich der Messkopf (ꙮ) des Messgerätes in der unteren Darstellung links in ca. 2m über der Wiese. G spezifiziert sich durch den betrachteten Wellenlängenbereich:
Darstellung 2: Algorithmus zur Ein- Ausstrahlung nach dem Göttinger Modell.
Die langwellige Strahlung „…ist vor allem eine terrestrische Strahlung, die von Emittern mit Temperaturen von unter 300K ausgeht. Es wird unterschieden zwischen: der Gegenstrahlung A […] der Ausstrahlung des Erdbodens E =εlw σTB4 …“ 6 7 Bei nichtmetallischen Leitern wird εlw zu 1. E und entspricht dann dem Begriff der Surface Radiation von KT97. Qlw ist der Saldo der langwelligen Strahlungsbilanz.
Qlw = A – σTB4 = A – E – Rlw
Qlw findet in der langwelligen Strahlung seine Analogie in der rechten Bildhälfte von FIG 7, KT97
Rlw = (1-εlw)
Rlw = 0 mit εlw = 1
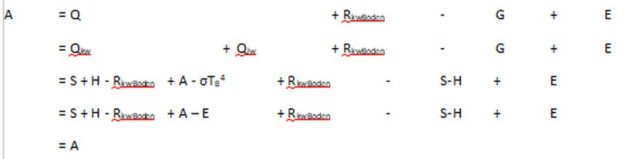
„Als Strahlungsbilanz Q bezeichnet man die Summe von Qkw + Qlw.
Q = Qkw + Qlw = S + H – RkwBoden + A – E – Rlw = … “ 8
Damit würde sich die Gegenstrahlung A ermitteln zu: A = Q + RkwBoden – G + E (d)
Beispiel 1:
Als Durchschnittswert für den Globus für den kurzwelligen Bereich nach Tabelle 6:
UV + sichtbares Licht errechnen sich zu 107.9 W/m² + 610.9 W/m² = 718.8W/m² = 719 W/m²
Man könnte danach als Messung der kurzwelligen Strahlung einen Wert von ca. 719 W/m² annehmen.
Der Albedogesamtwert sei a = 0,3129, nach KT97. Das Messergebnis für die AlbedoBoden sei für dieses Beispiel 0.135, siehe CLEAR SKY ALBEDO von ERBS als durchschnittlicher gemessener globaler Wert. T sei 14,80 °C und damit E = 390 W/m². Mit Rundung auf 0.5W/m² folgt:
G = S + H =
Rkw = AlbedoBoden (S +H) = 0.135 x 123.5W/m² = 17 W/m²
Qkw = S + H – Rkw = 123.5 W/m² – 17 W/m² = 106.5 W/m²
Qlw = A – σTB4 = A – E = 324W/m² – 390 W/m² = – 66W/m², A und E nach KT97 FiG. 7. rechte Bildhälfte
Q = Qkw + Qlw = 106.5W/m² – 66W/m² = 40.5 W/m²
A = Q + Rkw – G + E = 40.5 W/m² + 17 W/m² – 123.5W/m² + 390 W/m² = 324 W/m² = Gegenstrahlung
Beispiel 2:
Mit einem Messgerät waren auf einer Hamburger Wiese (54 Grad nördlicher Breite) nach Versuch 4, gemäß Göttinger Katalog didaktischer Modelle 9 nachfolgende Werte in W/m² ermittelt worden.
Global Strahlung S+H 104
Reflexstrahlung (Wiese) Rkw 20
kurzwellige Bilanz Qkw 84
atmosph. Gegenstrahlung A 320
langw. Emission E 357
langwellige Strahlungsbilanz Qlw -37
Gesamte Strahlungsbilanz Q 47
Temperatur T 8.50 °C
In Versuch 4 gemäß Göttinger Katalog ist für derartige Messgeräte ebenfalls ein üblicher Wertebereich für die kurzwellige Strahlung: 0.25 bis 3 µm angegeben. Da ein derartiges Gerät auch über 0.75µm misst, siehe Tabelle 6, reicht der Messbereich auch tief in den langwelligen infraroten Bereich hinein.
Betrachtet man den Albedoverlauf von 1985 -1990 an Satellitenbildern von ERBS (CEDA) über die geografische Breite, stellt man fest: Am Äquator hat die durchschnittliche Jahresalbedo, gemittelt über 12 Monate, ein Minimum (Wasser a = ca. 0.18 Land a = ca. 0.30). Zu den Wendekreisen steigt die Albedo aber deutlich an. Bei 54 Grad nördlicher und südlicher Breite erreicht die durchschnittliche Jahres Albedo einen Wert von ca. a = 0.40.  Eine gemessene langwellige Emission von 357W/m² entspricht einer Temperatur von 8.50 °C (Hamburg). Dies ist auch die Jahres Durchschnittstemperatur für Hamburg aus 12 Monaten Tag- und Nachtmessung. Das Messgerät wurde gemäß Versuchsanordnung nicht auf eine Schneefläche im Winter, sondern auf einer Wiese vermutlich im Frühling, Sommer oder Herbst aufgestellt. Dies lässt bei einer Temperatur für 8.50 °C (Frühling, Sommer oder Herbst) vermuten, dass bei der Messung der Himmel bewölkt war. Die Durchschnittsalbedo (gemittelt aus sonnig und bewölkt gemittelt) müsste für eine vermutete reine Bewölkung einen etwas höheren Wert aufweisen. Ein entsprechender Albedowert für die Berücksichtigung sei nun a = 0.43.
Eine gemessene langwellige Emission von 357W/m² entspricht einer Temperatur von 8.50 °C (Hamburg). Dies ist auch die Jahres Durchschnittstemperatur für Hamburg aus 12 Monaten Tag- und Nachtmessung. Das Messgerät wurde gemäß Versuchsanordnung nicht auf eine Schneefläche im Winter, sondern auf einer Wiese vermutlich im Frühling, Sommer oder Herbst aufgestellt. Dies lässt bei einer Temperatur für 8.50 °C (Frühling, Sommer oder Herbst) vermuten, dass bei der Messung der Himmel bewölkt war. Die Durchschnittsalbedo (gemittelt aus sonnig und bewölkt gemittelt) müsste für eine vermutete reine Bewölkung einen etwas höheren Wert aufweisen. Ein entsprechender Albedowert für die Berücksichtigung sei nun a = 0.43.
AlbedoBoden = Rkw / (S +H) = 20 / 104 = 0.1923
RkwBoden = Albedo (S +H) = 0.1923 x 104W/m² = 20 W/m²
Qkw = S + H – RkwBoden = 104 W/m² – 20 W/m² = 84 W/m²
Qlw = A – σTB4 = A – E = 320W/m² – 357 W/m² = – 37W/m²
Q = Qkw + Qlw = 84W/m² – 37W/m² = 47 W/m²
A = Q + RkwBoden – G + E = 47 W/m² + 20W/m² – 104W/m² + 357 W/m² = 320 W/m²
Betrachtet man (d) zur Ermittlung der Gegenstrahlung, dann fällt aber auf:
Die Variablen S, H, der Ausdruck RkwBoden der Bodenalbedo und Variable E der Strahlung aus der Boden Temperatur kürzen sich weg. Die Gegenstrahlung A ist somit unabhängig von der kurzwelligen Strahlung und deren Variablen. Die Gleichung (d) ist bezüglich A beliebig. Aber A ist selbst beliebig, da A, die Gegenstrahlung, aus einer Null bei KT97 und Barkstorm entstanden war (Nachweis siehe Kap 4.10 Mathematischer Effekt in 16). Dadurch ist es möglich das Messergebnis der kurzwelligen Messung aus 1367W/m² beliebig zu multiplizieren z.B. 0.25 = ¼. Um in Beispiel 2 (Versuch 4 des Göttinger Katalogs) als Summe von Sonnenstrahlung S und diffuser Strahlung H mit 104W/m² erhalten zu können, ist vorab bereits der Treibhauseffekt durch den ¼ Strahlungsverteilungsansatz im Messgerät hinterlegt. Derartige Geräte messen aber auch den langwelligen Strahlungsbereich. Diese Messgeräte weisen die Gegenstrahlung, zuweilen auch als thermische atmosphärische Strahlung bezeichnet, dann langwellig aus.
Hierzu findet sich in der nachfolgende Herstellerangabe eines anderen Pyranometers, wörtlich: „Das CM22 Pyranometer ist mit einem Thermosensor ausgestattet. Dieser spricht auf die insgesamt aufgenommene Energie an und ist theoretisch nichtselektiv gegenüber der spektralen Verteilung der Strahlung. Dies hat zur Folge, dass der Sensor auch gegenüber langwelliger Infrarotstrahlung (Wärmestrahlung > 4000 nm) aus der Umgebung (z.B. des inneren Doms) empfindlich ist.“ 11 [Hervorhebungen hinzugefügt] Derartige Geräte unterliegen einer Normung und sind daher in sich ähnlich gebaut und vergleichbar.
Über 4000 nm bzw. 4µm würde der Präzision Pyranometer CM22 theoretisch nicht, eventuell praktisch schon selektiv, nicht nur Bereiche der von der Sonne eintreffenden Langwellen messen, sondern auch die Bereiche der Umgebungstemperatur. Wenn am Tag Teile der „langwelligen Infrarotstrahlung“ in die Messung eingehen ist dies bei einer nächtlichen Messung konsequenter Weise ebenfalls der Fall.
Welche Konsequenz hat dies im Beispiel 1?
Was wird vermutlich ein solches Gerät als Gegenstrahlung messen?
Aus 1367W/m² verbleiben für den langwelligen Anteil: 1367W/m² – 719 W/m² = 648W/m²
Gegenstrahlung A = 648 W/m² – E + Qlw = 648 W/m² – 390 W/m² + 66 W/m² = 324 W/m²
Damit entspricht der gemessene langwellige Teil genau der Gegenstrahlung!
Welche Konsequenz hat dies im Beispiel 2?
Aus 1367W/m² verbleiben für den langwelligen Anteil: 1367W/m² – 727 W/m² = 640W/m²
Was wird vermutlich das Gerät als Gegenstrahlung messen?
Gegenstrahlung A = 640 W/m² – E + Qlw = 640 W/m² – 357 W/m² + 37 W/m² = 320 W/m²
Auch hier entspreche der gemessene langwellige Teil genau der vom Messgerät ausgewiesenen Gegenstrahlung!
Woraus entsteht die langwellige Strahlung 390 W/m² in Beispiel 2?
Das Hamburger Messgerät der Gegenstrahlung aus dem in situ Versuch misst den kurzwelligen Anteil (0.25 bis 3µm) der Strahlungsflussdichte in W/m² der einfallenden Sonnenstrahlung. Welcher Teil aus dem gesamten einfallenden Sonnenspektrum verbleibt? Es ist der langwellige Bereich von 760nm – 106 nm. Er weist nach Tabelle 6 eine Strahlungsflussdichte von 648.2 W/m² auf.
In Beispiel 2 wird auch ein messbarer, langwelliger Anteil des Gerätes von (3µm bis 100µm) 12 ausgewiesen. Dieser Bereich von 3000nm – 105 nm des zum Himmel gerichteten Messgerätes erfasst aus vorhanden Spektrum von 760nm – 106 nm nur einen Teilbereich der von der Sonne eintreffenden Langwellen, bei 320 bis 324 W/m² (Gegenstrahlungsmesswerte) etwa die Hälfte der vorhandenen Strahlungsflussdichte von 648.2 W/m² Langwelle.
Hieraus folgt:
-
Wenn der Treibhauseffekt, der durch eine angebliche, hypothetische Gegenstrahlung entsteht, bereits im Messgerät hinterlegt ist, dann kann mit diesem Messgerät der Treibhauseffekt nicht bewiesen werden. (Zirkelschluss)
-
Die Analyse der Grundlagen der Strahlungsmessgrößen in Verbindung mit dem Treibhauseffekt von 33K, nach der Studie KT97, in Verbindung mit einer Auswertung eines in situ Versuches in Anhang 4 von 16 lassen den folgenden Schluss zu: Ein großer langwelliger Bereich der auf der Erde eintreffenden Sonnenstrahlen wird stattdessen als langwellige Gegenstrahlung im Messgerät als Gegenstrahlung ausgewiesen.
-
Die gemessene Gegenstrahlung stammt bei Messungen am Tag offensichtlich zu 100% direkt aus der Sonne, von ihrem langwelligen Anteil mit 648.2 W/m² (Tabelle 6, WMO 1986). Bei einer nächtlichen Messung ist anzunehmen, dass Teile der Umgebungstemperatur als Gegenstrahlung mit ausgewiesen werden.
Nach Rödel 13 kämen „ungefähr 60% bis 65% der am Boden empfangenen Gegenstrahlung aus der Schicht zwischen dem Boden und etwa 100m Höhe, d.h. aus einer Schicht, die kaum kälter als die Erdoberfläche selbst ist.“ Der Temperaturabfall nach der Internationalen Höhenformel beträgt 0.65 °C auf 100m Höhe. Auch diese Aussage macht die Ausweisung von Teilen der Umgebungstemperatur als Gegenstrahlung nachvollziehbar.
Ergebnis zur Messung der Gegenstrahlung:
Für den kurzwelligen Bereich ist im Algorithmus derartiger Messgeräte der Treibhauseffekt von KT97 über die ¼ Strahlungsverteilung hinterlegt. Wenn man die langwellige Umgebungstemperatur des Messgerätes gemeinsam mit erheblichen Teilen der langwelligen Sonnenstrahlung, ab 3µm oder 4µm, herstellerabhängig, als Gegenstrahlung bezeichnet und dann als solche ausweist, stammt die Back Radiation final direkt aus der Sonne und der Wärme des Messgerätes und nicht aus IR-aktiven, infrarot absorbierenden und emittierenden Molekülen, wie CO2, H2O, CH4,.. . Sogenannte Messgeräte zur Gegenstrahlung sind deshalb nicht in der Lage, diese zu beweisen.
Ergänzung:
Auch über verschiedene Integrationen (Polarkoordinaten / kartesische Koordinaten) kann nachgewiesen werden, dass die Gegenstrahlung des Treibhauseffektes auf einer falschen Strahlungsverteilung bereits bei B. Barkstorm beruht, Nachweise siehe Kapitel 5.1.2, 5.18 sowie Anhängen 1 bis 3 in 16. Bezüglich Net-Strahlung des ERBS Satelliten und ihre Berücksichtigung in der Modellierung, ihre Bedeutung und Interpretation wird in diesem Zusammenhang auf Kapitel 5.4.2 – 5.4.5 und Anhang 6-8 in 16 ausführlich eingegangen. In Kapitel 5 wurde ein neues Modell entwickelt und der Modellierung von KT97 entgegengestellt. KT97 wird als falsche Modellierungshypothese widerlegt. Der Autor folgt einem Wissenschaftsverständnis nach Karl Popper, siehe Kap. 1.14 16. Es sei erwähnt: Die Satelliten ERBS, TERRA und AQUA zeigen so im neuen Strahlungsmodell und mit einer neu abgeleiteten Atmosphärengleichung H = S0/2 (1-α) – LH – SH – Satm – σTe4 = 0, es gibt keine Strahlungsbehinderung durch eine Gegenstrahlung A, sichtbar in FIG. 8a und FIG. 8b ebenfalls in Verbindung mit Kap. 5.18 16. Auch unter geologischen Gesichtspunkten (snowball earth hypothesis) ist ein Treibhauseffekt nicht erfoderlich, Nachweis siehe Kapitel 9.7 und seinen Unterkapiteln in 16. Mit dieser neuen Atmosphärengleichung ergibt sich ein Strahlungsverteilungsfaktor von ½. Nach diesem kurzen Exkurs erfolgt die Rückkehr zum Göttinger Modell der Gegenstrahlungsmessung.
Angewendet auf Beispiel 2 ergeben sich folgende Rechenwerte:
Rkw = Albedo (S +H) = 0.1923 x 208W/m² = 40 W/m²
Qkw = S + H – Rkw = 208 W/m² – 40 W/m² = 168 W/m²
Qlw = A – σTB4 = A – E = 0W/m² – 390 W/m² = – 390W/m²
Q = Qkw + Qlw = 168W/m² – 390W/m² = -222 W/m²
A = Q + Rkw – G + E = -222 W/m² + 40 W/m² – 208 W/m² + 390 W/m² = 0 W/m²
Würde man in derartigen Messgeräten der Gegenstrahlung den internen Algorithmus, also die hinterlegten physikalischen Gleichungen, auf der nach dem Autor richtigeren Strahlungsverteilungsfaktor ½ abändern, würde das Messgerät auch einen Gegenstrahlungswert von 0 ausweisen. Es kann gezeigt werden, dass die Divergenzen im Modell von J. Kiehl und K.E. Trenberth 1997 und J. Kiehl, J. T. Fasullo, K.E. Trenberth 2009 und den Satellitenmesswerten mit einer anderen Modellierung auf kleiner gleich 2 W/m² verschwinden, siehe Kapitel 5.1.2 folgende Kapitel 5.17 und Anhang 7 und 8 16.
Zusammenfassung:
Die Gegenstrahlung ist eine reine Modellhypothese aber Basis der aktuellen IPCC-Klimamodelle. Sie kann nicht gemessen werden, da der Treibhauseffekt durch den zugrunde gelegten Algorithmus bereits voreingestellt ist. Dies ist ein klassischer Zirkelschluss, oder anders formuliert, die Aussage ist bereits selbst Voraussetzung des Nachweises. Die Falsifizierung von KT 97 in 14 widerlegt den Treibhauseffekt und ihre Gegenstrahlungshypothese – von etwa 300 W/m² und höher – mit mathematischen, physikalischen / thermodynamischen Nachweisen und mit einem CO2– Experiment unter Sonnenlicht.
1J. Kiehl, J. T. Fasullo, K.E. Trenberth, 2009, Earth´s Global Energy Budget, Bulletin of the American Meteorological Society, March 2009, S.311-316f und Doi:10.1175/2008BAMS2634.I.
2Loeb, Dutton, Wild et altera, 2012, The global energy balance from a surface perspective, published online 13 November 2012, Clim Dyn (2013) 40:3107-3134, Springer-Verlag, Doi: 10.1007/s00382-012-1569-8.
3Prof. Möllner, Detlev, (2003), Luft, Chemie Physik Biologie Reinhaltung Recht, Walter de Gruyter, New York, ISBN 3-11-016431-0, Tab 2.3, S.126.
4Nach Wikipedia: „Ein Pyrgeometer […] dient der Messung der aus dem Halbraum eintreffenden atmosphärischen Gegenstrahlung, …“ https:/de.m.wikipedia.org/wiki/Pyrgeometer Stand vom 11.07.2020.
6http://wwwuser.gwdg.de>konzept/strahlungsmessung Versuch 4, S1.
7Der Spektralchemiker, Dr. Heinz Hug vertritt hierzu den Standpunkt: „Ob man vom Stefan-Boltzmann ausgehen darf, darüber lässt sich streiten, denn Stefan-Boltzmann setzt Homogenität voraus. Eine Wasseroberfläche hat eine andere Stefan-Boltzmann-Emission als ein Wald, Steppe, Wüste, …“ Quelle aus persönlicher Korrespondenz mit Dr. Hug vom 10 Juli 2020.
8http://wwwuser.gwdg.de>konzept/strahlungsmessung Versuch 4, S2.
9http://wwwuser.gwdg.de>konzept/strahlungsmessung Versuch 4, S1.-S.8.
10Nach CEDA, siehe IX und http://dap.ceda.ac.uk.thredds/fileServer/badc/CDs/erbe/erbedata/erbs/mean1985/albedo.gif Stand vom 28.5.2020.
11Kipp & Zonen B.V. Delft, Niederlande, Bedienungsanleitung Precision Pyranometer CM 22, Version 0803 (2003), S.1bis S. 64, Kap 1.2 Physikalische Grundlagen des Pyranometers, S.8.
12http://wwwuser.gwdg.de>konzept/strahlungsmessung Versuch 4, S1.
13Prof. W. Roedel, Prof. Th. Wagner, 2011, Physik unserer Umwelt: Die Atmosphäre, 4 Auflage, 1. korrigierter Nachdruck, Springer Verlag, ISBN 978-3-642-15728-8, Kapitel 1 Strahlung und Energie in dem System Atmosphäre/ Erdoberfläche, S.48.