Die sogenannte „gemessene globale Durchschnittstemperatur“ wird von den Ozeanen bestimmt
„Insbesondere erblicken wir in dem System der fossilen Klimazeugen keinen empirischen Anhalt für die Annahme, daß die von der Sonne ausgehende Strahlung sich im Laufe der Erdgeschichte geändert habe. Desgleichen fehlt es an Tatsachen, welche durch Änderung der Durchstrahlbarkeit der Atmosphäre (Arrhenius) oder des Weltalls (Nölke) zu erklären wären; …“
Daran hat sich bis heute nichts geändert, denn die Klimawissenschaft ist seit nunmehr knapp 100 Jahren mit einem eindeutigen Beweis für diesen vorgeblichen „natürlichen atmosphärischen Treibhauseffekt“ nicht vom Fleck gekommen. Vielmehr basiert das Bild der Klimawissenschaft von unserer Erde noch immer auf einer „Erde ohne Atmosphäre“, wie sie Julius von Hann im Jahre 1897 beschrieben hatte, Sekundärzitat mit Dank an Dr. Gerhard Kramm (Fairbanks, Alaska):
«Denken wir uns die Erdoberfläche ganz vom Fest-land eingenommen und ohne Atmosphäre, also etwa in dem Zustande, in dem sich der Mond befin-det, so würde die Wärmeverteilung auf derselben überall nur von der jedem Orte zukommenden Quantität der Sonnenwärme und dem Betrage der Wärmeausstrahlung daselbst abhängig sein. Da nun diese beiden Faktoren für alle Orte auf demsel-ben Parallel- oder Breitekreise dieselben sein müß-ten, so würden die Erdgürtel gleicher Wärme mit den Breitekreisen zusammenfallen. Selbst die Exis-tenz einer wasserdampffreien Atmosphäre würde an dieser Wärmeverteilung wenig ändern, bloß die absoluten Quantitäten der Wärme-Einstrahlung und -Ausstrahlung an der Erdoberfläche würden dadurch beeinflußt.»
Und um jetzt den Unterschied zwischen einer „Erde ohne Atmosphäre [und Ozeanen]“ einerseits und andererseits den Messwerten von einer realen Erde zu erklären, hatte man schließlich den ominösen „natürlichen atmosphärischen Treibhauseffekt“ erfunden. Dieser Effekt soll auf einer sogenannten „atmosphärischen Gegenstrahlung“ beruhen, die wiederum dem 2. HS der Thermodynamik widerspricht.
Es stehen hier also zwei konkurrierende Modelle für unsere reale Erde zur Diskussion:
Das Faktor4-Tag=Nacht-THE-Flacherdemodell mit einem „natürlichen atmosphärischen Treibhauseffekt“ (THE) der etablierten Klimawissenschaft auf dem Stand des 19. Jh.:
Reale Erde = „Erde ohne Atmosphäre“ + THE
Der Ketzer Weber behauptet im 21. Jh. dagegen, es gäbe gar keinen THE:
Reale Erde = Hemisphärisches S-B-Modell ohne THE
Wir setzen jetzt die beiden Modelle für die „reale Erde“ gleich und erhalten die Alternativen:
„Erde ohne Atmosphäre“ plus THE = Hemisphärisches S-B-Modell ohne THE
Und welches von beiden Modellen ist nun wohl richtig?
Das Dilemma der exakten Atmosphärenwissenschaft sind Tag und Nacht, die von der Jahreszeit bestimmte breitenabhängige Tageslänge sowie die physikalischen Einheiten für Leistung und Arbeit. Die üblichen klimawissenschaftlichen Darstellungen der solaren Einstrahlung auf unserer Erde umfassen seit mehr als einem Jahrhundert lediglich die taggenaue örtliche Gesamtstrahlungsmenge der Sonne über die gesamte Erdoberfläche, sogar inklusive der Elliptizität der Erdbahn; einige dieser Beispiele hatte ich hier diskutiert. Bei einem solchen 24h-Durchschnitt der solaren Arbeit ist dann physikalisch allerdings Endstation. Unbeleuchtete Flächen und zeitliche Ableitungen haben in einer S-B-Inversion nämlich nichts zu suchen, und daher müssen wir uns bei der Betrachtung der Sonneneinstrahlung auf die Tagseite unserer Erde beschränken.
Zur Erinnerung, ich hatte in meinen beiden DGG-Veröffentlichungen (2016 und 2019) diesen sogenannten „natürlichen atmosphärischen Treibhauseffekt“ als Ergebnis einer fehlerhaften Faktor4-Inversion des Stefan-Boltzmann-Gesetzes widerlegt. Unter anderem hatte ich das hier noch einmal näher ausgeführt und einen konkreten Nachweis geliefert, dass unbeleuchtete Flächen in einer Inversion des Stefan-Boltzmann-Gesetzes nichts zu suchen haben, Zitat:
„Es gibt im streng ‚gleichzeitigen‘ Stefan-Boltzmann-Gesetz keine Flächen (B), die nicht zur Strahlungsleistung (P) des Schwarzkörpers beitragen. Daher sind auch keine unbeleuchteten Flächen (B) in einer ‚gleichzeitigen‘ S-B-Inversion erlaubt. Physikalisch ‚gleichzeitig‘ bedeutet übrigens auch nicht, dass unterschiedliche ‚Gleichzeitigkeiten‘ in einer einzigen S-B-Berechnung aufaddiert und gemittelt werden dürften.“
ALSO: Der Faktor4-Tag=Nacht-THE-Flacherdeansatz leitet sich aus der durchschnittlichen solaren ARBEIT über den 24h-Tag her. Ein solcher Tag+Nacht-Durchschnittswert der solaren Strahlungsleistung hat aber überhaupt nichts mit der Temperatur auf unserer Erde zu tun, wie ich hier bereits ausführlich erläutert hatte. Denn von der 24h-durchschnittlichen Arbeit führt nun einmal kein physikalisch korrekter Weg mehr zurück zur Ermittlung der tatsächlichen spezifischen solaren Strahlungsleistung auf der Tagseite unserer Erde.
Aus einer solchen rückgerechneten 24h-Tag&Nacht-Durchschnittsleistung der Sonneneinstrahlung hatten erstmals Kramm et al. (2017) eine breitenabhängige Ortstemperatur (Kramm et al. (2017) Abbildung 22a) vorgelegt. Dieser Wert entsteht aus der Division der eingestrahlten solaren 24h-Gesamtenergie geteilt durch die Sekunden@24h pro Quadratmeter, die eigentliche physikalische Einheit ist also 1 J/(m² s). Folgerichtig ergibt die Ableitung einer Temperatur aus einer solchen 24h-durchschnittlichen Rückrechnung der solaren Strahlungsleistung durch die Einbeziehung der unbeleuchteten Nachtseite eine „Schneeball-Erde“ mit gefrorenen tropischen Meeren und einem Temperatur-Hotspot am Pol der jeweiligen Sommerhemisphäre, wie man das ebenfalls in der nachfolgenden Abbildung 1b ablesen kann.
In seiner E-Mail vom 29.01.2021 um 09:58 Uhr* an mich und den üblichen Skeptiker-Email-Verteiler hatte dieser Dr. Gerhard Kramm schließlich ein PDF-Dokument „kramm_bemerkungen_weber_v3.pdf“ (wird in der Folge als „Kramm 2021“ bezeichnet) mit einem direkten Vergleich zwischen meinem hemisphärischen S-B-Modell und seiner „Erde ohne Atmosphäre“ verschickt. Die beiden nachfolgenden Abbildungen entstammen diesem PDF:
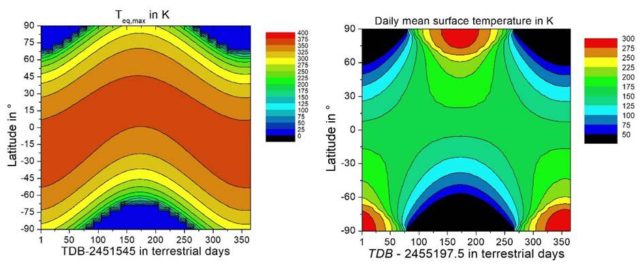
Abbildungen 1 a und b*: Berechnete Oberflächentemperaturen aus dem PDF-Dokument „kramm_bemerkungen_weber_v3.pdf“ von Dr. Gerhard Kramm, Fairbanks, Alaska*
Anmerkung: Die Temperaturskalen dieser Abbildungen stimmen nicht überein.
Originalbeschreibung: „Abbildung 15. Wie in Abbildung 12, jedoch für die auf dem lokalen Strahlungsgleichgewicht nach Gleichung (3) beruhende Oberflächentemperatur.“
Dazu der Text zu Abbildung 12: „Berechnete solare Einstrahlung für alle Tage des Jahres und alle geographischen Breiten:
(a [links]) Maxima nach Weber, beginnend mit dem 1. Januar 2000, 12:00 Uhr (JD = 2451545),
(b [rechts]) Tägliche Mittelwerte nach Kramm et al. (2017), beginnend mit 1.Januar 2010, 00:00 Uhr (JD =2455197,5).“
Die „Maxima nach Weber“ in der linken Abbildung, abgeleitet aus dem Maximum der örtlichen solaren LEISTUNG [W/m²] ohne Albedo, schwanken mit dem jahreszeitlichen Sonnenstand um den Äquator („Latitude 0°“) mit bis zu 394 Kelvin. Sie reduzieren sich dann zum Pol der Winterhemisphäre gegen null Kelvin. In der Realität werden diese theoretischen Maximalwerte aber aufgrund von Albedo, Verdunstung und Konvektion nicht erreicht; die Minimalwerte werden dagegen durch Advektion und Kondensation gestützt.
Die „Tägliche[n] Mittelwerte nach Kramm et al. (2017)“ in der rechten Abbildung, abgeleitet aus einer 24h-durchschnittlichen solaren ARBEIT [J/m²s] ohne Albedo, stellen dagegen die äquatoriale Zone bei 150-200 Kelvin mit gefrorenen tropischen Meeren als „Snowball-Earth“ dauerhaft im ewigen Eis dar; dafür verwandelt sich die Polarregion der jeweiligen Sommerhemisphäre in einen Touristen- und Temperatur-Hotspot mit 275-300 Kelvin.
Allein unser Schulwissen sagt uns also schon, welche der beiden Abbildungen am ehesten den Verlauf der Klimazonen unserer Erde spiegelt und dass der Pol der jeweiligen Sommerhemisphäre gar kein globaler Temperatur-Hotspot ist. Meine Ausführungen dazu hatte ich in dem EIKE-Artikel „Verbesserungswürdig: Über fehlerhafte Ansätze für eine breitenabhängige Globaltemperatur“ vom 18. März 2020 ausführlich dargestellt.
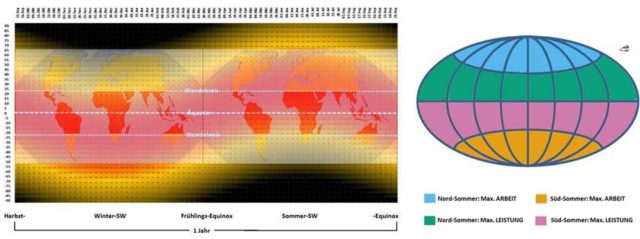
Abbildung 2: Zum physikalischen Unterschied zwischen Leistung (Watt) und Arbeit (Joule) der solaren Einstrahlung (Graphiken nicht flächengetreu)- Links: Tentative Gegenüberstellung der Beleuchtungsklimazonen mit dem Jahresverlauf der maximalen solaren Strahlungsleistung im Sommerhalbjahr (Südsommer linke Hälfte und Nordsommer rechte Hälfte). Overlays: Die Beleuchtungsklimazonen der Erde, von oben/unten zur Mitte: Polarzonen, Mittelbreiten, Tropenzone (Quelle: Wikipedia, Autor: Fährtenleser, Lizenz: GNU Free Documentation License) Darunter: Das örtliche Maximum der breitenabhängigen temperaturwirksamen spezifischen Strahlungsleistung der Sonne für die gesamte Erde über ein volles Jahr von Herbstäquinoktium zu Herbstäquinoktium- Rechts: Die maximale spezifische solare (Strahlungs-) LEISTUNG (~S-B-Temperaturäquivalent) und die maximale solare ARBEIT (Arbeit=Leistung x Zeit über die örtliche Tageslänge) im jeweiligen Sommerhalbjahr auf der Nord- und Südhalbkugel (weitere Erläuterungen sind hier zu finden)
Auf unserer Erde wandert der senkrechte Sonnenstand im Verlauf des Jahres zwischen den beiden Wendekreisen und verursacht so die gegenläufigen Jahreszeiten auf der Nord-und Südhemisphäre. Das maximal mögliche rechnerische S-B-Temperaturäquivalent der solaren Strahlungsleistung (@W/m²) folgt diesem vertikalen Sonnenstand, also von der Sonnenwende am Wendekreis der jeweiligen Sommerhemisphäre über den Äquator mit dem Äquinoktium zum gegenüber liegenden Wendekreis und wieder zurück. Polare Temperatur-Hotspots dagegen existieren nicht, es gibt in der Polarzone der Sommerhemisphäre lediglich eine tageszeitlich länger eingestrahlte solare Energiemenge [J/m²], die dort zu einer erhöhten Biomasse-Produktion im Sommerhalbjahr führt.
Also schauen wir mal, was wir sonst noch über die sogenannte „gemessene globale Durchschnittstemperatur“ herausfinden können
Betrachten wir jetzt einmal, wie sich die Tagseite (A) und die Nachtseite (B) auf die sogenannte „gemessene globale Durchschnittstemperatur“ von vorgeblich 14,8°C auswirken. Denn diese Durchschnittstemperatur NST kann über ihren 24h-Verlauf eigentlich nur ganz minimal schwanken. Schließlich soll dieser Wert aus weltweit zeitgleich ermittelten Temperaturen berechnet werden und bildet deshalb für jeden Zeitpunkt des 24h-Tages einen globalen Tag&Nacht-Durchschnitt ab. Die Tagseite (A) und die Nachtseite (B) der Erde sind an diesen Durchschnittswerten also gleichberechtigt beteiligt. Lediglich die unterschiedliche geographische Verteilung von Land- und Ozeanflächen und deren Position zum aktuellen Stand der Sonne dürften einen merklichen Einfluss auf den globalen tages- und jahreszeitlichen Temperaturdurchschnitt ausüben.
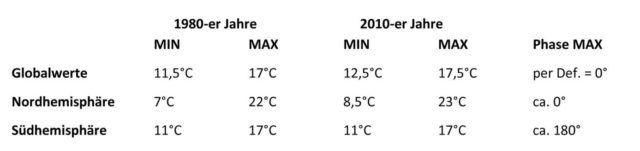
Es ist etwas ärgerlich, aber die „gemessenen“ Globaltemperaturen werden üblicherweise als Differenzen zu einem Referenzzeitraum angegeben, sodass eine echte Zuordnung oder gar die Überprüfung von konkreten Aussagen kaum noch möglich ist. Diesem Vorgehen liegt sicherlich keine böse Absicht zugrunde, Zusammenhänge zu verschleiern oder gar fehlerhafte Aussagen zu stützen. Auf meteo.plus findet man schließlich eine Copyright-geschützte Abbildung mit dem Verlauf der absoluten Globaltemperaturen seit 1979 bis heute, und zwar aufgeteilt in Globaltemperaturen sowie die Temperaturen von Nord- und Südhemisphäre, deren grobe Durchschnittswerte nachstehend aufgeführt sind:
Tabelle 1: Globale Durchschnittswerte der Temperatur (Daten von meteo.plus)
Im Ergebnis schwankt die Globaltemperatur also zwischen 12°C und 17°C, und im langjährigen Durchschnitt liegt sie bei etwa 14,5°C. Sie verläuft in Phase mit der Temperatur der Nordhemisphäre, und zwar mit dem Mittelwert der jeweiligen Temperaturen von Nord- und Südhemisphäre, beispielsweise als MED(MIN-Nord, MAX-Süd) oder MED(MAX-Nord, MIN-Süd).
In einer ersten groben Näherung können wir also die Nord-Temperatur den Landmassen und die Süd-Temperatur den Ozeanen zuordnen, wohl wissend, dass eine reine Land-Temperatur eine noch größere Schwankungsbreite hätte und eine reine Ozean-Temperatur eine noch geringere; Willis Eschenbach gibt übrigens die Schwankungsbreite der reinen Landtemperatur mit 15°C und die der Ozeane mit 5°C an. Was bei den meteo.plus-Daten allerdings in beiden Fällen bleibt, ist eine Mitteltemperatur von etwa 14,5°C, die der sagenhaften „gemessenen globalen Durchschnittstemperatur“ (NST) von 14,8°C recht nahe kommt. Und in seiner E-Mail vom 11.04.2021 um 23:47 Uhr an den Skeptiker-Verteiler verweist Kramm auf einen Artikel von Lockyer, „Studies of temperature and pressure observations„, der 1906 in Nature erschien war. Darin heißt es, Zitat:
« It is interesting to remark that the northern hemisphere appears to be 1.5 °C warmer than the southern. Spitaler in 1886 came to a similar conclusion, his figures being :-
[Der Google-Übersetzer: Es ist interessant festzustellen, dass die nördliche Hemisphäre 1,5 ° C wärmer zu sein scheint als die südliche. Spitaler kam 1886 zu einem ähnlichen Ergebnis, seine Zahlen waren:- ]
Northern hemisphere …..15.4 °C,
Southern hemisphere….. 14.8 °C,
Whole earth………………. 15.1 °C,
Excess of N. over S. ………0.6 °C.»
Die „Whole-earth-Temperatur“ von Spitaler (1886) liegt also bei etwa 15°C. Da bleibt die Frage, wie überhaupt die „aktuelle globale Erwärmung bereits bei etwa 1 Grad Celsius“ über einer „vorindustriellen Durchschnittstemperatur“ liegen kann, wo doch in der Gegenwart immer noch sogenannte Globaltemperaturen um 15°C herum gemessen werden. Schließlich können für die Zeit vor 1886 gar keine neuen Temperaturmessungen mehr dazugekommen sein…
Meinem hemisphärischen S-B-Modell für unsere reale Erde wird von diversen Kritikern eine Nachttemperatur von 0 Kelvin nachgesagt. Nun erhält die Nachtseite unserer realen Erde zwar keinerlei Sonneneinstrahlung, aber trotzdem herrscht dort keine Mond-Temperatur von etwa minus 200°C. Vielmehr befindet sich die Temperatur unserer Erde in einem „eingeschwungenen“ Zustand. Lediglich die Differenz zur minimalen Nachttemperatur muss täglich ersetzt werden (hier letzte Abbildung). Denn die Nachttemperatur eines passiv bestrahlten Himmelskörpers hängt im Wesentlichen von dessen Wärmespeicherfähigkeit ab. Und auf unserer Erde wird der Nachtseite die erforderliche Wärme von ihrer kombinierten Luft-Wasser-Heizung aus den globalen Zirkulationen (Atmosphäre und Ozeane) zur Verfügung gestellt. Allein die Ozeane, die zwei Drittel unserer Erdoberfläche bedecken, enthalten ein Wärmeäquivalent von etwa 50.000 24h-Tagen Sonneneinstrahlung; und diese Wärmespeicher (Atmosphäre und Ozeane) werden wiederum fortwährend durch die solare Einstrahlung auf der Tagseite unserer Erde „aufgeladen“. In der nachfolgenden Abbildung ist links die jahresdurchschnittliche Oberflächentemperatur der Ozeane dargestellt, also der Durchschnitt zwischen Tag und Nacht sowie Frühling, Sommer, Herbst und Winter – mit entgegengesetzten Jahreszeiten auf beiden Hemisphären:
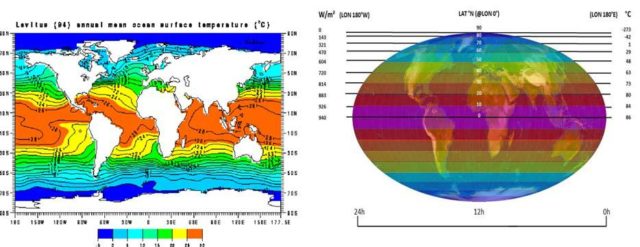
Abbildung 3: Temperaturvergleich Ozeane und S-B-Temperaturäquivalent der solaren Einstrahlung. Links: “Annual Mean Ocean Surface Temperature” based on observed data up until 1994 (NASA). Rechts: Das maximale breitenabhängige S-B-Temperaturäquivalent über den 24h-Tag im Äquinoktium, das aufgrund von Verdunstung und Konvektion nirgendwo erreicht wird
Mit angepasster Mollweide-Projektion (Copyright L. Rohwedder – Lizenz CC BY-SA 3.0)) Darüber: Das örtliche Maximum der breitenabhängigen temperaturwirksamen spezifischen Strahlungsleistung der Sonne für die gesamte Erde über einen 24h-Tag im Äquinoktium
ALSO noch einmal ganz langsam zum Mitdenken: Die Sonne muss unsere Erde gar nicht jeden Morgen von 0 Kelvin auf Tagestemperatur bringen. Die Erde befindet sich nämlich in einem „eingeschwungenen“ Zustand und ihre Wärmespeicher sind mit dem Äquivalent von mehr als 50.000 24h-Tagen Sonneneinstrahlung gefüllt. Diese Wärmespeicher verlieren also nachts „nur etwas“ Energie und müssen deshalb auf der Tagseite lediglich „nachgefüllt“ werden, mehr nicht. Im Mittel sprechen wir hier von 1,05*10^22 Joule, die die Erde über den durchschnittlichen 24h-Tag netto erhält und auch wieder abstrahlt. Denn sonst wäre die sogenannte „gemessene“ globale Durchschnittstemperatur (NST) nicht einigermaßen stabil. Herr Werner Schulz hatte die KKDML-Fraktion mit pädagogischem Langmut immer wieder darauf hingewiesen, dass auf der Tagseite im Mittel* 480W/m² kontinuierlich eingestrahlt und 240W/m² kontinuierlich über die Gesamtfläche der Erde abgestrahlt werden. Abgestrahlt werden also jeweils 240W/m² auf der Tagseite und 240W/m² auf der Nachtseite – das ergibt in Summe dann wieder 480W/m² Abstrahlung, also gilt: IN=OUT.
*) Für die Sophisten unter Ihnen: Korrekt wäre bei der Einstrahlung eine Summierung über (S0(1-Albedo)* COSZenitwinkel). Ich verwende hier nach KT97 weiterhin 940W/m² für (S0(1-ALBEDO)); in meinen DGG-Veröffentlichungen beschreibe ich dagegen einen Zweischichtfall.
Die solare Einstrahlung ersetzt also lediglich die terrestrische Abstrahlung bei einer „gemessenen globalen Durchschnittstemperatur“ (NST) von etwa 15°C, die sich wiederum ohne einen „natürlichen atmosphärischen Treibhauseffekt“ ganz zwanglos aus meinem hemisphärischen S-B-Ansatz herleitet. Es gilt demnach im langjährigen Durchschnitt:
[ Solare Einstrahlung @2PIR² = terrestrische Abstrahlung @4PIR² ] @ NST
Unsere Erde verfügt auf zwei Dritteln ihrer Oberfläche über eine Fußbodenheizung mit der in Abbildung 3 (links) dargestellten mittleren Vorlauftemperatur. Diese Ozean-Temperaturen repräsentieren wiederum zwei Drittel der „gemessenen“ globalen Ortstemperaturen. Die mittlere jährliche Oberflächentemperatur der Ozeane liegt bis etwa 70° nördlicher und südlicher geographischer Breite zwischen 0°C – 30°C und fällt erst jenseits davon auf bis zu -5°C ab; ein globaler Durchschnitt dürfte also in etwa bei der NST von etwa 15°C kumulieren. Wie wir bereits erfahren haben, wird das maximale rechnerische S-B-Temperaturäquivalent meines hemisphärischen S-B-Modells aufgrund von örtlicher Konvektion und Verdunstung in der Realität nirgendwo erreicht. Andererseits sinkt die Temperatur der Winterhemisphäre, insbesondere in der Polarnacht, niemals auf das rechnerische S-B-Temperaturäquivalent der geringen/fehlenden solaren Einstrahlung ab. Die nachfolgende Abbildung zum globalen horizontalen Wärmetransport gibt Aufschluss über die Gründe dafür:
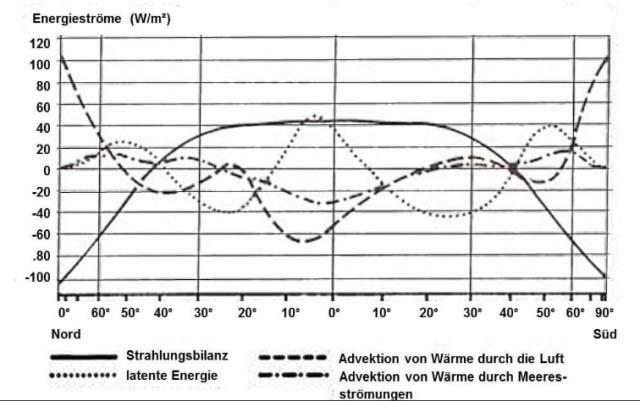
Abbildung 4: Jahresmittel des Energiehaushaltes der Atmosphäre und seiner Komponenten in Abhängigkeit von der geographischen Breite. QUELLE: HÄCKEL, Meteorologie, Verlag Eugen Ulmer, Stuttgart 1990, hier aus dem Internet
Alle diese Energieströme summieren sich für eine feste geographische Breite im durchschnittlichen Jahresmittel gerade auf null. Wir können hier also erkennen, dass sich die Überschüsse und Defizite gegenüber dem hemisphärisch berechneten S-B-Temperaturäquivalent durch den lateralen Transport von Wärme gerade global ausgleichen und damit mein hemisphärisches S-B-Modell voll bestätigen.
Wenn wir jetzt abschließend in der nachfolgenden Abbildung noch einmal die beiden Modell-Temperaturverläufe mit den Beleuchtungsklimazonen unserer Erde vergleichen, dann finden wir estätigt, dass unser Schulwissen über diese Klimazonen gar nicht mal so schlecht ist:
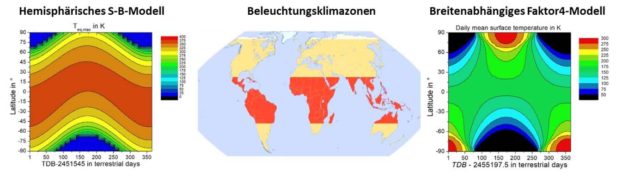
Abbildung 5: Vergleich unterschiedlicher Modelle für die globale Verteilung der Temperatur. Links mein hemisphärisches S-B-Modell: Oberflächentemperatur für die solaren Strahlungsmaxima nach Weber aus Kramm (2021)*. Mitte: Die Beleuchtungsklimazonen der Erde: von oben/unten zur Mitte: Polarzonen, Mittelbreiten, Tropenzone – (Quelle: Wikipedia, Autor: Fährtenleser, Lizenz: GNU Free Documentation License). Rechts ein breitenabhängiges 24h-Temperaturmittel: Oberflächentemperatur für die solaren tägliche Mittelwerte nach Kramm et al. (2017) aus Kramm (2021)*
Ergebnis: Unserem profanen Schulwissen ist an dieser Stelle wohl nichts mehr hinzuzufügen. Wie erwartet, spiegeln die Beleuchtungsklimazonen (Definition) unserer Erde (Abbildung 5 Mitte) den Verlauf der maximalen örtlichen solaren Strahlungsleistung. Und diese solare Strahlungsleistung ist in den Tropen am höchsten und fällt dann zu den Polarregionen kontinuierlich ab. Von den beiden konkurrierenden theoretischen Klimamodellen in Abbildung 5 wird dieser natürliche Verlauf lediglich von meinem hemisphärischen S-B-Modell korrekt abgebildet. Mein hemisphärisches S-B-Modell aus dem 21. Jahrhundert ersetzt als realistisches Modell unserer Erde ohne THE also das Faktor4-Tag=Nacht-THE-Flacherdemodell der real existierenden Klimawissenschaft mit einem fehlerhaft konstruierten „natürlichen atmosphärischen Treibhauseffekt“ von konstant 33°C.
*) Nachtrag: Um jedweden Beschwerden vorzubeugen, bestätige ich hiermit, ein direkter „An“-Adressat der o. g. E-Mail vom 29. Januar 2021 um 09:58 Uhr mit Kramms PDF-Dokument „kramm_bemerkungen_weber_v3.pdf“ und den dort enthaltenen Abbildungen 15 a und b (hier Abb. 1 a und b sowie Abb. 5 links und rechts) zu sein, ebenso, wie u. a. auch die Herren Lüdecke, Limburg und Kirstein. Ich beweise nachfolgend mit der „Confidentiality Warning“ des Dr. Gerhard Kramm die rechtmäßige Nutzung dieser Graphiken in meinem Artikel „Die sogenannte ‚gemessene globale Durchschnittstemperatur‘ wird von den Ozeanen bestimmt“, Zitat:
“CONFIDENTIALITY WARNING: The information transmitted is intended only for the person or entity to which it is addressed and may contain confidential and/or privileged material. Any review, retransmission, dissemination or other use of, or taking any action in reliance upon, this information by persons or entities other than the intended recipient is prohibited. If you receive this in error, please contact the sender and delete the material from any computer.”
Der unbestechliche Google-Übersetzer bestätigt mir ausdrücklich, die Inhalte der besagten E-Mail Kramm vom 29. Januar 2021 um 09:58 Uhr rechtmäßig zitiert zu haben:
„VERTRAULICHKEITSWARNUNG: Die übermittelten Informationen sind nur für die Person oder Organisation bestimmt, an die sie gerichtet sind, und können vertrauliches und / oder privilegiertes Material enthalten. Jegliche Überprüfung, Weiterverbreitung, Verbreitung oder sonstige Verwendung oder Ergreifung dieser Informationen durch andere Personen oder Organisationen als den beabsichtigten Empfänger ist untersagt. Wenn Sie dies irrtümlich erhalten, wenden Sie sich bitte an den Absender und löschen Sie das Material von einem beliebigen Computer.
ERGO: Es verbleiben für eine erlaubte „Überprüfung, Weiterverbreitung, Verbreitung oder sonstige Verwendung oder Ergreifung dieser Informationen“ ausschließlich die von Dr. Kramm „beabsichtigten Empfänger“, und ich bin definitiv der ERSTE „AN“-EMPFÄNGER dieser E-Mail.