Ist die „amtlich verordnete Panik“ übertrieben? Eine mathematische Analyse

Die Sterbefallzahlen von 2006 bis 2019 zeigt die folgende Tabelle:

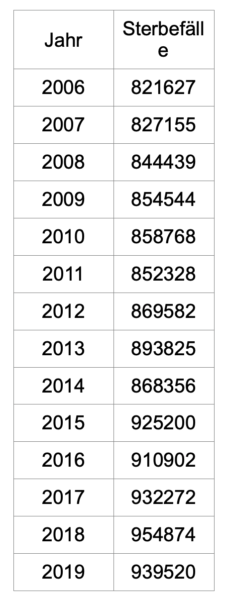
Die steigende Tendenz ist nicht zu übersehen und wird noch deutlicher, wenn man die Daten in ein übliches Streudiagramm einträgt.

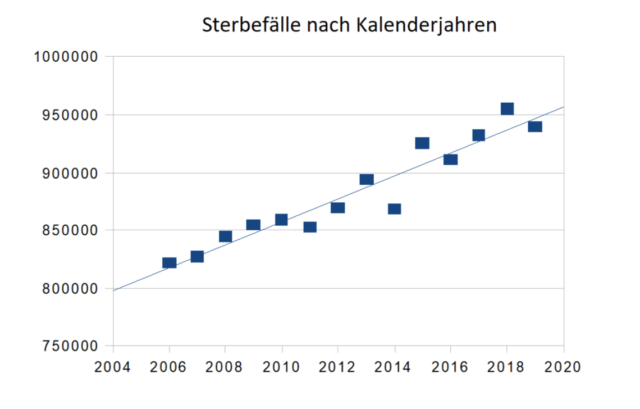
Zusammen mit den Punkten, die den jeweiligen Datenpaaren aus der Tabelle entsprechen, wurde die Regressionsgerade eingezeichnet, gewonnen mit der üblichen Methode der linearen Regression. Die deutliche lineare Tendenz sieht man schon mit bloßem Auge, doch man muss sich zum Glück nicht auf das bloße Auge verlassen. Um den Grad der Übereinstimmung der gegebenen Daten mit dem linearen Verlauf in Zahlen zu fassen, kann man den Korrelationskoeffizienten r berechnen. Dafür gibt es eine nicht allzu unangenehme Formel, die man auch bei Bedarf komplett umgehen kann, indem man einfach die entsprechende Excel-Funktion verwendet. Heraus kommt in beiden Fällen das Gleiche, nämlich r=0,957. Um das klarzustellen: Bei einem steigenden Verlauf kann r nicht größer als 1 sein, und der Wert 1 bedeutet, dass die Punkte alle auf einer Geraden liegen, während der Wert 0 anzeigt, dass die Daten keinerlei lineare Tendenz aufweisen. Der Wert r=0,957 liegt nun sehr nahe bei 1, woraus folgt, dass es eine annähernd lineare – und zwar ansteigende – Tendenz bei der Anzahl der Sterbefälle in Deutschland gibt. Woran immer das liegen mag: Bisher hat es noch niemanden nennenswert gestört, schon gar nicht hat man darin einen Grund für einen Lockdown gesehen.

Nun muss man natürlich nicht bei der Grafik stehenbleiben, man kann auch die Gleichung der Regressionsgeraden ausrechnen und erhält ohne großen Aufwand die Formel fälle=9949,468 * jahr – 19140919,47. Dabei handelt es sich nicht um die gezählten Fälle, sondern um die Anzahl der Sterbefälle, die nach dem linearen Trend jeweils zu erwarten wären. Um den erwarteten Trendwert zu berechnen, muss man also nur die gewünschte Jahreszahl mit dem Faktor 9949,468 multiplizieren und dann die Zahl 19140919,47 abziehen. Für das Jahr 2013 ergibt das beispielsweise eine vermutete Zahl von 9949,468 * 2013 – 19140919,47 = 887359,61, also von 887360 Sterbefällen, die von der korrekten Zahl 893825 um 6465 nach unten abweicht. Für jedes Jahr kann man nun die Abweichung ausrechnen und dann den Durchschnitt der Absolutbeträge bilden mit dem Resultat einer durchschnittlichen Abweichung von 9467 Fällen. Alternativ kann man auch die jeweilige prozentuale Abweichung ausrechnen und damit feststellen, wie weit das echte Ergebnis vom Trendwert abweicht, indem man die absolute Abweichung durch den Trendwert teilt. Das ergibt dann eine durchschnittliche prozentuale Abweichung von 1,06%.

Interessant ist nun, was sich für das Jahr 2020 ergeben müsste, wenn man den Trend, der sich nun seit 14 Jahren sehr stabil gezeigt hat, einfach fortrechnet. Das ist leicht, man muss nur das Jahr 2020 in die obige Formel einsetzen und erhält den Prognosewert 957006. Genau so viele Sterbefälle wären also 2020 zu erwarten, wenn sich der gut bestätigte Trend ohne weiteren äußeren Einfluss fortsetzt und die Entwicklung sich genau an das lineare Szenario hält. Das ist selbstverständlich nicht anzunehmen, aber für eine realistischere Einschätzung liegen ja die durchschnittlichen Abweichungen vom Trend vor. Verwendet man die absoluten Abweichungen, so ergibt sich der Bereich zwischen 957006 – 9467 = 947539 und 957006 + 9467 = 966473. Wirft man nun noch einmal einen genaueren Blick auf die Grafik, so stellt man fest, dass auf ein eher mildes Jahr tendenziell ein härteres Jahr folgen dürfte, was auch dem allgemeinen Prinzip der Regression zum Mittelwert entspricht. Somit wäre ein Ergebnis zwischen 957006 und 966473 Sterbefällen für das Jahr 2020 völlig normal und mit den Daten der Jahre 2006 bis 2019 problemlos vereinbar. Legt man die prozentuale Abweichung von 1,06% zugrunde, so ergibt sich für das Jahr 2020 sogar eine im üblichen Durchschnitt liegende Abweichung von 10144, womit man den oberen Wert 957006+10144=967150 erreicht.

Wie man auch rechnet, es ergibt sich, dass im Jahre 2020 eine zwischen 957000 und 967000 liegende Zahl von Sterbefällen in Deutschland völlig im Rahmen der Sterbedaten der Jahre 2006 bis 2019 liegen würde. Betrachtet man nun die bisher ermittelte Anzahl der Sterbefälle, die man beim Statistischen Bundesamt heute, am 27.12.2020, 12 Uhr, bis zum 22.11.2020 tagesgenau aufgelistet findet, so ergibt sich eine Zahl von knapp 850000 bisherigen Sterbefällen, genauer gesagt sind es 849982. Vom 23.11. bis zum 31.12.2020 verbleiben 39 Tage, und nach der oben ausgeführten Rechnung sollte man im Normalfall mit weiteren 107000 bis 117000 Sterbefällen innerhalb dieser 39 Tage rechnen, umgerechnet sind das 2744 bis 3000 Todesfälle pro Tag. Bis zum 22.11.2020 lag die Zahl der durchschnittlichen Sterbefälle pro Tag bei ziemlich genau 2600. Am Ende des Jahres wird man sehen, was die letzten 39 Tage noch beigetragen haben. In jedem Fall ergibt sich unter Beibehaltung des Trends die Prognose von 957000 bis 967000 Sterbefällen für das Jahr 2020, mit deren Eintreten man im Normalfall rechnen müsste.

Sollte nun die Gesamtzahl der Sterbefälle den Wert 967000 nicht übersteigen, könnte man auf die Idee kommen, dass die amtlich verordnete Panik doch etwas übertrieben war. In diesem Fall gibt es also im Laufe des Jahres nicht mehr Sterbefälle, als man nach den Entwicklungen der letzten 14 Jahre erwarten sollte, sie haben sich unter Umständen nur auf andere Todesursachen verteilt. Das gerne vorgebrachte Argument des Präventionsparadoxons, nach dem nur die harten Maßnahmen zu einer auch unter normalen Umständen erwartbaren Sterberate geführt habe, kann dann nicht angewendet werden, denn trotz aller Maßnahmen wird noch immer Tag für Tag eine hohe Zahl mutmaßlich neu Infizierter gemeldet, die aber im Falle der vermuteten Sterberate keinen nennenswerten Einfluss auf die Gesamtzahl der Toten gehabt haben können – die Rate liegt dann ja im Rahmen des auch ohne Infektionsfälle Erwartbaren.

Und natürlich gilt auch hier: eventuelle Übertragungs-, Rechen-, Denk- oder Interpretationsfehler sind durchaus nicht ausgeschlossen und ausschließlich mir anzulasten.

Gastbeiträge geben immer die Meinung des Autors wieder, nicht meine. Ich schätze meine Leser als erwachsene Menschen und will ihnen unterschiedliche Blickwinkel bieten, damit sie sich selbst eine Meinung bilden können.

Über den Autor

Thomas Rießinger ist promovierter Mathematiker und war Professor für Mathematik und Informatik an der Fachhochschule Frankfurt am Main. Neben einigen Fachbüchern über Mathematik hat er auch Aufsätze zur Philosophie und Geschichte sowie ein Buch zur Unterhaltungsmathematik publiziert.

Der Beitrag erschien zuerst bei Reizschuster.de hier