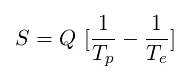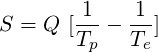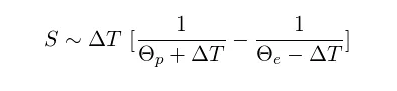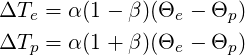Klimamodelle: Von warmen Polen und kalten Tropen

Eine der Freuden von Diskussionen mit Klimawissenschaftlern ist, dass man einen Einblick in ihre Denkweise bekommt. Nehmen Sie zum Beispiel das oft postulierte: „Man sollte sich das große Ganze ansehen“. Was viele Klimawissenschaftler damit meinen, ist die Betrachtung der neuesten super-duper Ozean-Atmosphäre gekoppelten Modelle mit zeilenweisen Strahlungstransfer-Codes und was nicht noch alles. Ohne das, so die Behauptung, kann man nicht verstehen, wie das Klimasystem funktioniert. Seltsamerweise bedeutet „das große Ganze betrachten“ für einen Physiker wie mich genau das Gegenteil: das zu betrachtende System auf das Wesentliche zu reduzieren und Erkenntnisse über sein Innenleben aus der zugrundeliegenden Physik zu gewinnen, ohne sich von Details ablenken zu lassen.

Was ist hier also das große Ganze? In ihrer einfachsten Form ist die Erde ein Wärmeübertragungssystem im Nicht-Gleichgewicht (aber in einem stabilen Zustand), in dem Wärme (überwiegend) in den Äquatorregionen eintritt und Wärme (überwiegend) an den Polen verloren geht. Im Inneren wird die Wärme durch atmosphärische und ozeanische Strömungen von den Tropen zu den Polen transportiert, wodurch die Tropen abgekühlt und die Polarregionen erwärmt werden. Ohne diesen Transport würde die lokale Temperatur nur durch das Gleichgewicht zwischen Sonneneinstrahlung und Strahlungsverlusten bestimmt, wodurch die Tropen wärmer wären als sie sind und die Pole kälter. Die Tropen sind kühler, als sie es ohne diesen Transport wären, während die Polarregionen wärmer sind. Daher: kalte Tropen und warme Pole.

Jetzt kommt das Rätsel: Der Wärmetransport zwischen Tropen und Polargebieten wird durch deren Temperaturdifferenz bestimmt. Je größer diese ist, desto größer ist der Wärmestrom. Der Wärmetransport verringert aber diese Temperaturdifferenz und wirkt damit seiner eigenen Verursachung entgegen. Betrachten wir z. B. den Grenzfall eines sehr großen Wärmestroms, bei dem die Wärmeübertragung praktisch augenblicklich erfolgt. Als Ergebnis hätten die Pole die gleiche Temperatur wie die Tropen, aber dann kann es überhaupt keinen Wärmestrom geben, weil dieser durch eine Temperaturdifferenz angetrieben wird. Wir haben also einen Widerspruch. Von der umgekehrten Situation auszugehen, dass es keinen Wärmestrom gibt, ist ebenfalls unhaltbar, weil die große Temperaturdifferenz einen Wärmestrom hervorruft. Es gibt aber einen Wärmestrom, der daher mit der von ihm verursachten Temperaturdifferenz konsistent sein muss. Ein kleinerer Temperaturunterschied ist nicht möglich, denn das würde den Wärmestrom verringern und damit die Differenz wieder vergrößern; und ein größerer Temperaturunterschied würde den Wärmestrom vergrößern und damit verringern. Dies deutet stark darauf hin, dass sich die Atmosphäre als Ganzes in einem Zustand einpendelt, in dem die Temperaturdifferenz zwischen den Tropen und den Polen minimal ist, während gleichzeitig der von ihr verursachte Wärmestrom zwischen ihnen maximal ist. Wir können diese Einsicht nutzen, um seine Größe zu berechnen, indem wir das Prinzip der Maximalen Entropieproduktion MEP anwenden, eine Arbeitshypothese in der Nicht-Gleichgewichtsthermodynamik, die zunehmend Unterstützung in Beobachtungen findet (siehe Kleidon für eine ausgezeichnete Einführung, Ref. 1, 2).

Das MEP-Prinzip besagt, dass ein System, das weit vom (thermodynamischen) Gleichgewicht entfernt ist, sich an einen stationären Zustand anpasst, in dem Energie dissipiert und Entropie mit der maximal möglichen Rate produziert wird. Beachten Sie, dass „maximale Entropieproduktion“ etwas völlig anderes ist als „maximale Entropie“. Letztere bezieht sich auf ein geschlossenes System im thermodynamischen Gleichgewicht. Hier haben wir es mit einem offenen System zu tun, das sich nicht im thermodynamischen Gleichgewicht befindet, sondern in einem stetigen Nicht-Gleichgewichtszustand.

Ich fürchte, ich muss hier einige Formeln einführen. Was ich tun werde ist, die Grundgleichung und ihre Lösung hier anzugeben, während ich für die Kenner der Materie in einem Anhang erläutere, wie man diese Lösung findet. Diejenigen, die mit der Thermodynamik vertraut sind, werden diesen Ausdruck für die Produktion, also die Änderung, dS der Entropie S durch eine Änderung des Wärmeinhalts dQ bei der Temperatur T kennen:

Hieraus folgt direkt die Formel für die Entropie-Produktion durch einen Wärmefluss Q zwischen den Äquator-Gebieten mit der Temperatur T_e und den Polen mit der Temperatur T_p:

Die Wärme verlässt die äquatorialen Regionen mit der Temperatur T_e, daher das Minuszeichen, und erreicht die Pole mit der Temperatur T_p. Die Maximierung von S ist gleichbedeutend mit der Suche nach der optimalen Kombination von Q und T_e -T_p. Die Lösung dieser Gleichung ist recht einfach (siehe Anhang). Die tatsächliche Differenz T_e -T_p beträgt fast die Hälfte der Differenz, die sich ohne Energiefluss ergeben hätte. Halb, also nicht 0,3 oder 0,7 mal.

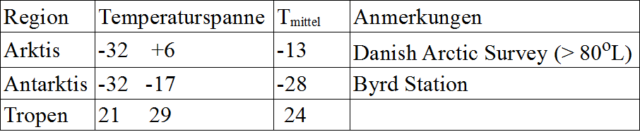
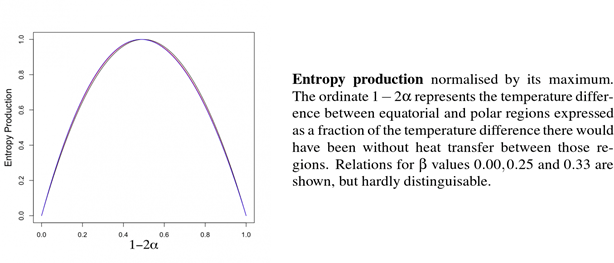
Testen wir dieses Ergebnis anhand von Modellen und Beobachtungen. Es scheint gut etabliert zu sein – aus Berechnungen mit Standard-Atmosphärenmodellen –, dass ohne den Wärmetransfer die äquatorialen Regionen etwa 15 Grad wärmer und die Pole etwa 25 Grad kälter wären (Celsius, ref 3). Ich nehme diese Abschätzungen für bare Münze; sie implizieren eine Asymmetrie β = 0,25, für die 1 – 2α ~ 0,51 gilt (siehe Anhang). Dann lautet die Vorhersage, dass der Temperaturunterschied zwischen den Tropen und den Polen mit dem Wärmetransfer etwa 41 Grad beträgt (also (15 + 25) × 0,51∕0,49), während der Unterschied ohne diesen Transfer etwa 80 Grad betragen würde. In der Tabelle sind einige reale Beobachtungen aufgeführt:

Für die Antarktis habe ich die Daten der Byrd-Station verwendet, weil sie auf einem Plateau liegt und daher vermutlich weniger von einer möglichen Abschirmung durch Berge betroffen ist. Die gemittelte polare Temperatur scheint bei etwa -21°C zu liegen. Für die Tropen entspricht das untere Ende des Bereichs überwiegend den ozeanischen Daten und sollte daher ein größeres Gewicht im Mittelwert haben, der hier mit 24°C angenommen wird. Die beobachtete Temperaturdifferenz zwischen polaren und äquatorialen Regionen liegt also bei etwa 45 Grad, gegenüber einer Vorhersage von 41 Grad. Nicht schlecht für ein so einfaches Modell.

Es mag ein einfaches Modell sein, aber das MEP-Prinzip hat eine wichtige Implikation. Die Maximierung der Entropieproduktion für stationäre Bedingungen impliziert eine starke negative Rückkopplung auf Störungen (siehe Kleidon). Jede Störung wird per Definition zu einer Abnahme von S führen, und das System wird sich anpassen und versuchen, es wieder zu optimieren. Eine solche Störung in Klimamodellen ist bekannt und seit langem etabliert und weithin als gültiges Konzept akzeptiert: die „polare Verstärkung“. Sie besagt, dass sich in einer sich erwärmenden Atmosphäre die Polarregionen schneller erwärmen als die äquatorialen Regionen; daher nimmt T_e – T_p ab. Es ist jedoch auch eines der seltsamsten Konzepte, die in der Klimamodellierung zu finden sind, weil es keine begrenzende Bedingung hat: Nirgendwo in der Literatur steht etwas wie „unter diesen und jenen Bedingungen, bei diesem Grad der Erwärmung, wird die polare Verstärkung aufhören“. Dies könnte zu einer Absurdität führen: Sollte die Atmosphäre heiß genug werden, würde der Temperaturunterschied zwischen Äquator und Pol komplett verschwinden oder sogar das Vorzeichen wechseln. Es muss also Bedingungen geben, unter denen die Verstärkung nicht mehr stattfindet. Warum ist das wichtig? Wenn es einen solchen Mechanismus gibt, der unter bestimmten Umständen einsetzt, dann muss man erklären, warum er gerade jetzt nicht funktioniert, und das könnte peinlich sein. Wie dem auch sei, aus dem Vorangegangenen sollte ersichtlich sein, dass das Konzept der polaren Verstärkung in der Tat ziemlich fragwürdig ist: Die verringerte Differenz von polaren und äquatorialen Temperaturen reduziert den Wärmefluss zu den Polarregionen, was eine Abkühlung zur Folge hätte. Ein realistisches Klimamodell sollte sich so verhalten, wie es die zugrundeliegende Physik vorgibt. Daraus lässt sich ableiten, dass eine solche Rückkopplung in den aktuellen Klimamodellen nicht vorhanden ist und dass folglich das ganze Konzept ein Artefakt eines unvollständigen Modells sein könnte. (Sie haben es hier zuerst gelesen.)

Aber wie das Leben so spielt hat sich die Arktis in den letzten 3 oder 4 Jahrzehnten erwärmt. Das würde das Konzept der polaren Verstärkung beweisen, oder? Nun, diese Erwärmung mag in der Arktis der Fall sein, aber sie sollte gleichzeitig auch für die Antarktis gelten, aber dort scheint das Konzept den Vergleich mit den Beobachtungen nicht zu bestehen (ref 4).

Was mag also in der Arktis vor sich gehen? Ich erlaube mir, hierzu meine Meinung zu verkünden. Für mich liegt der Schlüssel in der Tatsache, dass es zwei Pole gibt. Es wäre außergewöhnlich, wenn zu allen Zeiten genau der gleiche Anteil der äquatorialen Wärme auf jeden Pol verteilt würde. Die Übertragungsmechanismen, atmosphärische und insbesondere ozeanische Strömungen, sind von Natur aus chaotische Systeme, die dazu neigen, von einem bestimmten quasi-stabilen Strömungsmuster zu einem anderen zu wechseln. Bei den Meeresströmungen kennen wir dieses Verhalten als Pazifische Dekadische Oszillation, Atlantische Multidekadische Oszillation, Dipol des Indischen Ozeans und dergleichen. Die Zeitskala für solche Veränderungen beträgt viele Jahrzehnte, von 3 für die PDO bis zu 6-8 für die AMO, weil eine enorme Masse und ein enormer Impuls von sich bewegendem Wasser beteiligt ist und Wasser eine inkompressible Flüssigkeit ist, was bedeutet, dass die Veränderung über das gesamte Strömungsmuster gleichzeitig stattfindet. Daher ist zu erwarten, dass die Verteilung der Wärme nach Norden und Süden Änderungen auf einer Zeitskala von Jahrzehnten in einer erratischen Wippe unterliegt. Wir leben zufällig in einer Zeit, in der die nördliche Hemisphäre etwas mehr als ihren gerechten Anteil an der Wärme bekommt; in ein paar Jahrzehnten kann das ganz anders sein. Um solche Veränderungen von einem möglicherweise zugrunde liegenden langfristigen Erwärmungstrend zu unterscheiden, werden Daten über einen viel längeren Zeitraum benötigt, als wir jetzt haben.

Anmerkung von Dipl.-Met. Christian Freuer hierzu: die „bipolare Schaukel“ oder „- Wippe“ ist ihm vor Jahrzehnten schon einmal untergekommen, aber nur aufgrund von Beobachtungen und ohne dass die damaligen Autoren eine Erklärung dafür parat hatten. Es ist äußerst erhellend und erfreulich, hier in relativ einfacher Form jetzt endlich eine solche Erklärung dafür zu finden. – Ende Anmerkung

Link zum Original siehe unten. Bis hier Übersetzt von Chris Frey EIKE

References:

(1) Axel Kleidon (2009): ”Non-equilibrium thermodynamics and maximum entropy production in the Earth system”, https://link.springer.com/article/10.1007/s00114-009-0509-x

(2) A Kleidon, R D Lorenz (editors) ”Non-equilibrium thermodynamics and the production of entropy” (2005) Springer, ISBN 978-3-540-22495

(3) e.g. http://earthguide.ucsd.edu/virtualmuseum/virtualmuseum/EarthsClimateMachine.shtml

(4) e.g. https://wattsupwiththat.com/2019/04/10/the-curious-case-of-the-southern-ocean-and-the-peer-reviewed-journal/

Es folgt eine genaue theoretische Herleitung, deren Übersetzung ich hier mal weglasse. Anm. d. Übers.]

Solving the EP equation

The entropy production S for a heat flow Q between the equatorial regions of temperature T_e and the polar regions of temperature T_p is given by:

The MEP hypothesis is that the atmospheric system tends to maximise S. This optimum can be found analytically as follows. Introduce Θ_e and Θ_p, the temperatures of the equatorial and polar regions respectively if there were no heat transport. That is, Θ_e and Θ_p stand for the radiative equilibrium temperatures of those regions. The actual temperatures (T_e and T_p) are different because of the heat transport. Hence define ΔT_e = Θ_e – T_e and ΔT_p = T_p – Θ_p. Let’s for the moment assume that they are both equal and equal to a fraction α of the range Θ_e – Θ_p:

Notice that the difference T_e – T_p equals:

Obviously for α = 0 there is no heat transfer, hence S = 0, while for α = 0.5 we have T_e equal to T_p and thus no entropy production either. In between these extremes the heat flux Q is somehow proportional to ΔT_e, the larger the drop in temperature of the equatorial region, the larger the heat loss from it and one can assume the relation to be (close to) linear. This gives us an expression for S in terms of ΔT, hence as function of α :

The maximum of S in the range [0.0 – 0.5] is straightforwardly found with basic calculus techniques – you need to solve a cubic equation in α – and turns out to be almost exactly at α = 0.25. Alternatively, one could use the R analysis package, encode the function for S, find the maximum with Newton’s method and get a figure as a bonus.

The upshot of all this is that the MEP temperature difference T_e -T_p is very nearly half the difference Θ_e – Θ_p which we would have had in the absence of any heat flow.

Let’s now revisit ΔT_e and ΔT_p. Adopting equality of ΔT_e and ΔT_p means assuming that for every degree drop in temperature of the equatorial regions the polar temperature rises by one degree. This is not very realistic; quite likely the polar temperature rises more because of area and heat capacity differences. We can include such an imbalance by slightly modifying the definitions of ΔT_e and ΔT_p and introduce an asymmetry parameter β:

With a value of β = 0.25, for instance, this would mean that for every 3 degrees drop in equatorial temperature the poles would gain 5 degrees. Notice that the difference T_e – T_p remains as given earlier. Repeating the foregoing exercise for a range of β values presents us with an interesting result: the corresponding α values are practically unchanged: for β = 0 the maximum is at α = 0.2487, for β = 0.25 at 0.2441 and β = 0.33 at 0.2427. This means that irrespective of a possible asymmetry between equator and polar regions the temperature difference between the two remains firmly at about half the difference Θ_e – Θ_p, but that the centre of the range shifts according to the value of β

Link: https://wattsupwiththat.com/2020/12/21/of-warm-poles-and-cold-tropics/