Insbesondere die viel bekannten, oft zitierten, oft interviewten Klimaforscher wie z.B. der bekannte  Professor Stefan Rahmstorf verweisen bei ihren öffentlichen Vorträgen gern auf die strenge Wissenschaftlichkeit ihres Tuns.
So auch hier in seinem Vortrag in Mainz anlässlich der Reihe „Physik im Theater“ der Uni Mainz am 2.11.19 und anderswo. Sind sachkundige Leute im Saal, dann kommt gelegentlich die Frage, wie es denn möglich sei, eine globale Mitteltemperatur auf 2 Stellen hinter dem Komma, mit nur ± 0,05 ° Unsicherheit zu berechnen, wenn die ursprünglichen Daten selber nicht nur eine sehr viel größere Messunsicherheit von bestenfalls ± 0,5 ° brächten, aber auch vielfältige systematische Fehler diese weit in den Bereich von mehreren Grad verschöben.

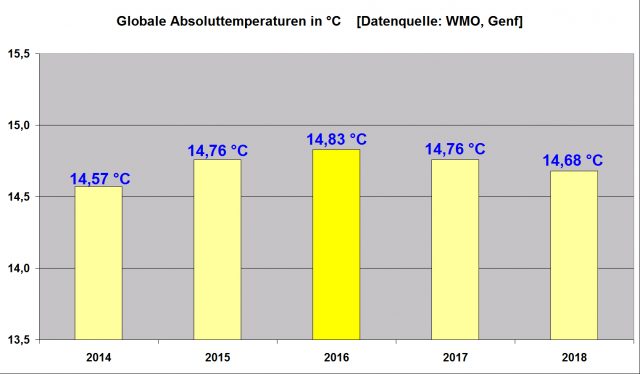
Die Antwort darauf ist eigentlich immer dieselbe. Sie lautet, weil man Differenzen (im Jargon: Anomalien) aus zwei Absolutwerten bilde, also den aktuellen Wert von einem Referenzwert abzöge, seien diese sehr viel genauer, weil, und das wird impliziert, wenn auch selten dazu gesagt, sich dann die Fehler von selbst aufhöben, weil ja beide Werte denselben Fehler trügen.
So auch Stefan Rahmstorf in besagtem Vortrag. Er sagte, dass nun mal die Anomalien sehr viel genauer seien, als die Absolutwerte, das sei wissenschaftlich klar belegt, und verwies in diesem Zusammenhang auf seine Website Spectrum.de Scilogs,wo er dieses ausführlich erklärt hätte.
Nun, schaut man dort nach, dann wird zwar ausführlich erläutert, dass es – seiner Meinung nach- nur auf die Veränderung, also die Anomalie, ankäme, aber, obwohl er vorher versprach „Licht ins Dunkle zu bringen“  lässt er seine Leser weiterhin im Dunkeln, behält also die versprochen Erleuchtung für sich und erklärt nichts.
Stattdessen wird dem Leser wortreich mitgeteilt, wie und auf welche  Weise die meteorologischen Rohdaten weltweit – wenn auch sehr spärlich in Raum und Zeit verteilt – gewonnen wurden, und weiter erklärt, dass verschiedene Institute sich weltweit mit deren Auswertung beschäftigten, was natürlich einen gebührenden Eindruck beim Leser hinterlässt, um dann noch stolz zu betonen, dass deren Ergebnisse „dabei in hohem Maße..“ übereinstimmten.
 

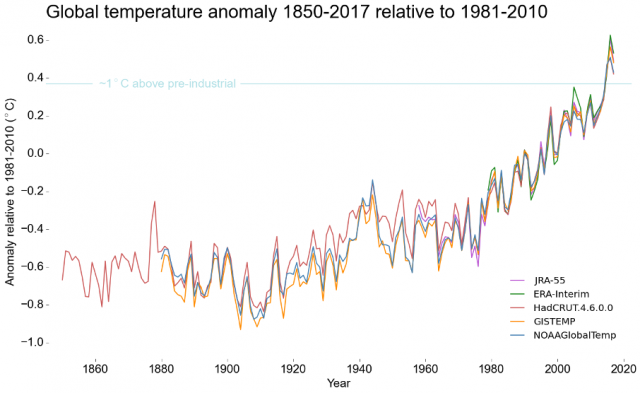
Dazu wird die Grafik (s.o) in Abbildung 2 gezeigt.
Die Übereinstimmung ist in der Tat gut, wie jeder sehen kann, erklärt aber immer noch nicht, warum die Anomalien genauer sein sollten als die Absolutwerte, zumal jede Unsicherheitsangabe in der Grafik fehlt. Und beschreibt damit eigentlich auch nur die Selbstverständlichkeit, dass wissenschaftliche Auswertungen von immer denselben Daten auch zu sehr ähnlichen, bis exakt gleichen Ergebnissen führen müssen. Bspw. muss jede Messung der Erdanziehung, egal wie sie durchgeführt wird, immer auf einen Wert von 9,81 m/s²kommen. Kleine Unterschiede, bedeuten dann entweder Fehler oder sind Hinweise auf geologische Anomalien.
Dann, etwas weiter im Text, verspricht Rahmstorf sich der eigentlichen Frage zu stellen:

„Warum sind Differenzen genauer als Absolutwerte?“

lautet zunächst vielversprechend die Überschrift des nächsten Absatzes.
Aber wiederum zeigt er dann nur, dass er wohl bis heute selber nicht verstanden hat, was er den Lesern da eigentlich erzählt. Denn als einzigen Beweis stellt er die Behauptung auf:

„Wohl jeder Wissenschaftler ist damit vertraut, dass man in vielen Fällen Differenzen bzw. Veränderungen einfacher bzw. genauer messen kann als Absolutwerte.“

Nun muss noch mal erwähnt werden, dass nur Absolutwerte gemessen und Differenzen aus eben diesen nur errechnet werden können. Doch das begreift Rahmstorf wohl nicht, denn als Beispiel führt er an:

„Um in Paris zu bleiben: gehe ich auf dem Eiffelturm eine Treppenstufe hinauf, kann ich leicht mit einem Lineal messen, wieviel höher ich dann stehe – aber wie viele Meter über dem Erdboden ich insgesamt bin, lässt sich schon schwerer feststellen.“

Das ist zwar eine schöne Metapher, aber erklärt nun wahrlich nicht, warum Differenzen einfacher bzw. genauer gemessen werden können als Absolutwerte. Denn was er so nett beschreibt ist exakt die Messung des Absolutwertes der Höhe dieser Treppenstufe.
Nichts anderes.
Und die hat natürlich die üblichen Fehler einer Messung mit einem Lineal im Zentimeterbereich.
Doch in einem hat er recht, von der Höhe der Treppenstufe lässt sich nun wirklich nicht ableiten, egal mit welcher Genauigkeit, wie hoch sich diese über Grund befindet. Dazu fehlt die zweite wichtige Angabe, nämlich deren absolute Höhe über Grund. Und die kann, ebenso wie die, die der Treppenstufe selber, nur absolut bestimmt werden.
Offensichtlich hat er bis heute nicht begriffen, dass er mit diesem Vergleich seine eigene Argumentation ad absurdum führt. Nämlich, indem er wieder einen Absolutwert bestimmt, und diesen jetzt fälschlich zur Differenz erklärt. Differenzen müssen nun mal aus den Absolutwerten gerechnet und können nicht gemessen werden, da beißt nun mal die Maus keinen Faden ab. Und dazu braucht man von den Grundrechenarten die Subtraktion A-B = C. C wird errechnet und enthält somit nach der Fehlerfortpflanzung die Summenfehler von A und B. Genauer, die Wurzel der Summe der Quadrate der Fehler von A+B.
Niemand misst die meteorologische Differenztemperatur in einer Wetterhütte.
In dem er also die Höhe der Treppenstufe misst, schafft er das Problem nicht aus der Welt, er vernebelt es nur.
Das allerdings tut er im Folgenden sehr wortreich. Zwischendurch konzediert er zwar, eher beiläufig, dass die Wetterstationen weltweit   .. den Absolutwert der Temperatur, also z.B. 13,1 °C oder –5,4 °C“messen, lenkt dann aber die Aufmerksamkeit des Lesers auf, in diesem Zusammenhang völlig unwichtige, Nebenkriegsschauplätze. Und merkt das vermutlich nicht einmal selber.
Um dann, statt Klärung und Beweis auf diesen allein wichtigen Punkt einzugehen, einfach  so zu behaupten,..

„Die klimatischen Veränderungen der Temperatur kann man dagegen viel genauer bestimmen: schon für die Monatsmittelwerte der globalen Temperatur auf plus oder minus einige Hundertstel Grad genau. Das liegt einfach daran, dass Abweichungen der Monatsmitteltemperatur großräumig korreliert sind: wie Datenanalysen ergeben haben über einen Radius von mehr als eintausend Kilometern (Hansen et al. 1999).“

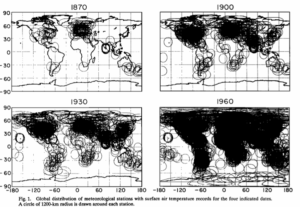
Abbildung 2: Verteilung der einbezogenen GHCN Messstationen nach Hansen & Lebedeff von 1870 bis 1960 sowie deren postulierte Abdeckung
Das war’s. Kein Beweis, keine Herleitung. Nur eine Behauptung.
Nun sind Korrelationen und Datenunsicherheiten zwei paar Schuhe, und der von ihm zitierte Herr Hansen hat sicher viel für die Klimapanik weltweit getan, aber in dessen hier zitierter Arbeit wird mit keinem Wort nachgewiesen, dass Anomalien genauer wären, als die ihnen zugrunde liegenden Absolutwerte. Es findet sich nichts darin,  gar nichts, sondern nur mehrfache Verweise auf eigene frühere Arbeiten, insbesondere auf Hansen und Lebedeff 1987[1].
Doch auch dort haben sie zwar die sehr kühne Behauptung aufgestellt, dass Wetterstationen, die bis zu 2400 km (1200 km Radius,) entfernt voneinander stünden, das ist immerhin die Entfernung Berlin – Malaga, immer hoch korrelierte Trends aufwiesen. Um im Umkehrschluss dann kühn zu folgern, dass deshalb nur einige wenige dieser Stationen ausreichten, um die globalen Trends der (Mittel-)Temperatur extrem genau zu berechnen. Und das, wie Rahmstorf seine Leser und Zuhörer glauben machen will „auf einige hundertstel Grad genau“. Aber auch dazu wiederum findet sich kein Wort, warum Anomalien genauer sein sollen, als ihre jeweiligen Bezugs- und Rechengrößen.
In einem meiner früheren Artikeln zum Thema (hier) in dem ich diese Aussage untersuchte, schrieb ich deshalb:

„Hansen ist auch derjenige, der 1988 dem amerikanischen Senat bei drückend heißem Wetter und unter tatkräftiger Mithilfe seines Kumpels -des Politprofis Al Gore- die Nachteile der künftigen vermutlich katastrophalen Erwärmung näherbrachte.
In einem Aufsatz von 1987 [3] im damals noch angesehenen JOURNAL OF GEOPHYSICAL RESEARCH durften die  Autoren  „peer reviewed“ verkünden, dass es dank ihrer Forschung möglich sei, aus der Not eine Tugend zu machen. Nämlich aus der Not keine flächenmäßig ausreichende Abdeckung mit Klimamessstationen zu haben, die Tugend, diese auch gar nicht zu brauchen. Und nur deswegen, weil man nun die Vorzüge von Korrelationen für unbekannte Trends einzusetzen imstande sei.“

…und über Fehler bzw. deren Größe und Korrektur findet man nur:

„In der Zusammenfassung des Aufsatzes steht:
“..Wir zeigen, dass die Temperaturen von Messstationen mittlerer und hoher Breite über 1000 km miteinander hoch korreliert sind. Bei Stationen in niederer Breite fällt die Korrelation mit der Entfernung stärker ab“
Und etwas später ebenda:
“.. Fehlerabschätzungen basieren in Teilen auf Studien wie genau die derzeitigen Stationsverteilungen in der Lage sind Temperaturänderungen in einem globalen Datensatz zu repoduzieren, die von einem dreidimensionalen GCM (General Circulation Model) mit realistischer Variabilität erzeugt wurden.“ 
In diesem hochtrabenden, etwas verschwurbelten Satz steht also im Klartext:
“ Wir haben eine Fehlerabschätzung (in Teilen? Welche Teile?) gemacht, indem wir die Ergebnisse mit Modellen, die „realistische“ Temperaturvariationen zuvor errechnet hatten, verglichen haben.“
Also nix mit Realitätsvergleich, nix mit Überprüfung der Daten der einbezogenen Stationen, sondern stattdessen Überprüfung mit Modellen! Der künftige modellverliebte Kurs der Klimaforschung des IPCC wurde hier schon vorgezeichnet. „

Und in diesem Beitrag „von Korrelationen und Anomalien“wird dann nochmals im Detail nachgewiesen, dass auch die Behauptung über die Nutzbarkeit von Korrelationen zur Trendbestimmung weit entfernter Stationen mit fehlerhaften Messungen absoluter Humbug ist.
Zitat (Willis Eschenbach) daraus

„Hansen und Lebedeff lagen richtig damit, dass die jährlichen Temperatur-Historien von weit auseinander liegenden Messstationen dazu neigen, gut korreliert zu sein. Allerdings lagen sie nicht richtig mit ihrer Meinung, dass dies für die Trends der gut korrelierten Temperatur-Historien gälte. Deren Trends können völlig ungleich sein. Im Ergebnis ist die Extrapolation von Trends aus einer bis zu 1200 km entfernten Messstation ein unzulässiges Verfahren ohne jegliche mathematische Basis.
Soweit der pfiffige, misstrauische Willis Eschenbach.“

Doch da Rahmstorf immer wieder denselben Unsinn erzählt, kann man wohl davon ausgehen, dass er vielleicht gelegentlich bei den Grundrechenarten etwas Nachhilfe benötigt, und von Fehlerrechnung – und -fortpflanzung auch nicht viel Ahnung zu haben scheint.
Denn Böswilligkeit, um mittels bewusst falscher Behauptungen seine Ideen zu verbreiten, will man ihm ja nun wirklich nicht unterstellen.
In diesem Zusammenhang möchte ich noch auf das ausgezeichnete Video vom Team Klimamanifest von Heiligenroth aufmerksam machen das den bezeichnenden Titel trägt

Das #Verwirrspiel des Stefan @Rahmstorf (V3a)

 

 
und sich intensiv mit der Verneblungstaktik im Wesentlichen von S. Rahmstorf beschäftigt, um nicht zugeben zu müssen, dass das Pariser Zweigradziel auf tönernen Füßen steht, bzw. ohne jede Grundlage ist. Es lohnt die Zeit zu investieren und es sich in ganzer Länge anzuschauen.
 
[1]Hansen, J. and Lebedeff, S., Global Trends of Measured Surface Air Temperature, J. Geophys. Res., 1987, 92 (D11), 13345-13372.