…siehe hier, hier und hier.“ (Pat Frank 9.12.2019[1])

Teil 1 hier und Teil 3 hier

Zu 3 Messregime

Da es praktisch undurchführbar war die gemessene Temperatur in kurzen Zeitabständen abzulesen, wünschenswert wären bspw. alle 5 Minuten gewesen, definierte man entweder wenige feste Tageszeiten, an denen abgelesen (und notiert) wurde, dies wurde insbesondere in Zentraleuropa – aber zu verschiedenen Zeiten und auch unterschiedlich oft- so gemacht, oder man las nur die Max. und die Min-Werte von speziellen Thermometern ab, und war dadurch zeitlich nicht so gebunden. Man handelte sich aber damit die Unkenntnis ein, nicht genau zu wissen, wann am Tag der Max. bzw. Min. Wert aufgetreten war. Das führte zu einem speziellen, aber kräftigen Fehler bei der Auswertung, der sogar einen eigenen Namen bekam, der Time of Observation Error (TOBs). Vor allem die praktischen Briten und mit ihnen dann alle ihre Kolonien und Einflussgebiete benutzten bis zum Ende des vergangenen Jahrhunderts diese Methode.

Abbildung 5 Kleine Auswahl aus historisch vielfach verwendeten Mittelwertbildungsalgorithmen
Aus diesen punktuellen Messwerten wurden dann arithmetische Mittelwerte gebildet, das sog. Tagesmittel. Diese (verschiedenen) Tagesmittel erlaubten nun Monatsgänge der Tagestemperaturen zu bilden. Sie wurden und werden dann weiter zu arithmetischen Monatsmitteln zusammengefasst, die es wiederum erlaubten Jahresgänge zu bilden, welche den Verlauf der Jahreszeiten anhand der Mittel-Temperatur zeigten.  Diese können dann zu Zeitreihen für langjährige klimatologisch interessante Zeiten zusammengefasst werden, was auch geschieht.
Es geschieht aber noch etwas anderes mit diesen Daten, sie werden in „Anomalien“ umgerechnet, d.h. es werden Differenzen aus dem aktuellen Wert abzüglich eines Referenzwertes gebildet. Dies geschieht wegen der berechtigten Annahme, dass Anomalien die eigentlich gesuchten Veränderungen präziser und weiträumig vergleichbarer abbilden, als die der absoluten Temperaturen, die zusätzlich noch weiteren Einflüssen wie Höhenlagen, windhöffiger oder stiller Messort etc. ausgesetzt sind. Doch damit handelt man sich neue Fehlerquellen ein, von denen die wenigsten Klimaforscher etwas wissen, ja schlimmer noch, die wegen falscher, wenn auch plausibler Analogien, zu völlig falschen Ergebnissen führen müssen. Welche das im Einzelnen sind und was das bedeutet wird im Teil „Weiterverarbeitung“ ausführlich beleuchtet.

Zu 4. Die geografische und zeitliche Abdeckung

Sobald die so gewonnenen Daten etwas mehr zur Beobachtung und Deutung von großräumigem Wettergeschehen herangezogen werden sollen, was in der Natur der Sache liegt, denn Wettergeschehen ist großräumig, kommt es unmittelbar auf eine genügende räumliche wie zeitliche Abdeckung der in Frage kommende Gebiete an. Doch da setzen ebenso technische wie finanzielle Machbarkeit enge Grenzen. Errichtung und Betrieb von Wetterstationen ist nicht nur teuer, sondern verlangt neben der genügenden Verfügbarkeit der richtigen Messmittel, auch genügend personelle Kapazität, großes Know How  und Disziplin für ihren Betrieb. Und das permanent über lange, im politischen Maßstab sehr lange Zeiträume. All das war von Anfang an nicht selbstverständlich und musste erst langsam nach dem Entstehen reifen. So wundert es nicht, dass die Stationsdichte sich ausnahmslos in früh entwickelten Ländern konzentriert, während weite Teile der Welt bis Anfang der 50er Jahre praktisch ohne Messstationen blieben. Das gilt für Südamerika, Afrika und weite Teile Asiens, ebenso wie die mehr als doppelt so große Ozeanfläche dieser Welt.

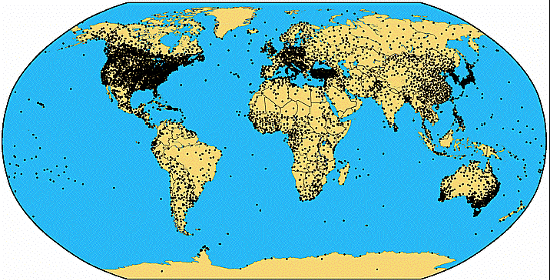
Abbildung 6 Entwicklung der Zahl und Position der historischen Messstationen
darunter Aktueller Stand der im Global Historical Climate Networks GHCN der NOAA mit Monatsmittelwerten der  Temperatur  insgesamt zuliefernden 7.280 Stationen mit mindesten 10 Jahren  kontinuierlicher Datenreihen. Für Stationen mit Max/Min Erfassung gibt es ähnliche Grafiken. Quelle (http://www.ncdc.noaa.gov/oa/climate/ghcn-monthly/index.php fig. 1). Man beachte jedoch, dass von GISS und CRU davon nur ungefähr 1/7 ausgewertet werden.
Quelle https://climateaudit.org/2008/02/10/historical-station-distribution/

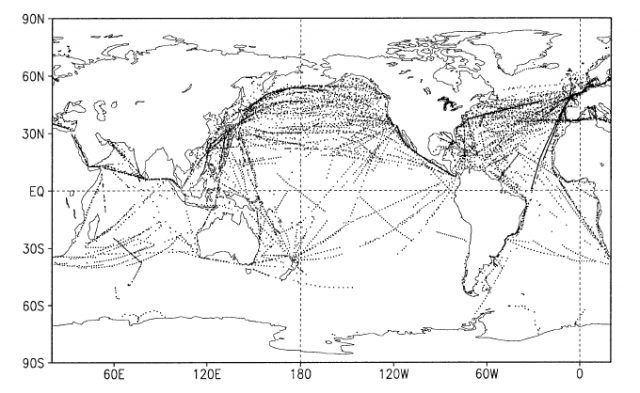
Abbildung 7 Darstellung der gemeldeten SST´s für die Woche vom 2. bis 8. Januar 2000. Sie zeigt die dünne messtechnische Abdeckung der Wasserfläche der Erde. Frühere Abdeckungen der Wasserfläche sind mit großer Wahrscheinlichkeit noch deutlich schlechter gewesen. Aus [REYNOLDS, R. W. & RAYNER,, 2002] Seite 1611
 

Zu 5. Die Weiterverarbeitung! Was geschieht mit den meteorologischen Messdaten?

Wie zuvor schon kurz angesprochen werden die Einzeldatensätze erst einer umfassenden Prüfung auf Konsistenz, Dauer, und Plausibilität, mit anschließender Weiterverarbeitung unterzogen. Zunächst bleibt es bei den einzelnen Stationen und ihren Daten. Je nach Verwendungszweck wird aus diesen erst Tagesmittel und daraus das Monatsmittel gebildet und von diesem eines als „Station Normal“ bezeichneten langjährigem (bspw. über 360 Monate also 30 Jahre) Mittel abgezogen. Die so entstehende Differenz wird als so gut wie fehlerfrei betrachtet, weil – so die Annahme – die lokalen systematischen Fehler ja auch im „Station Normal“ vorhanden seien, und, wenn man beide Werte voneinander abzöge, sich der Fehler kompensierte (stellvertretend dafür [Brohan et al. 2006])[2],[3]. Manchmal werden aber auch zunächst die Jahresmittel gebildet und diese vom „Station Normal“ abgezogen. Die Grundannahme aber, von der Fehlerselbstkorrektur bei Bildung von Anomalien, bleibt aber dieselbe.
Und daher behaupten so gut wie alle Klimaforscher, auch Stefan Rahmstorf vom PIK unwidersprochen[4], dass Anomalien viel genauer seien als die ihnen zugrunde liegenden Absolutwerte. Liest man seinen Text genauer, dann muss man feststellen, dass er sich mit der Materie nicht beschäftigt hat, sondern nur auf die Korrelation zwischen den Trends von absoluten Temperaturdaten verweist, wie sie schon von James Hansen für seine Schwarze Kunst verweist. Es bleibt ein bitterer Treppenwitz der Wissenschaftsgeschichte, dass Annahmen über Korrelationskoeffezienten herunter bis 0,33 (Hansens Grenzwerte) die Politik in ein nie dagewesenes Desaster treiben konnte.  Wer Näheres dazu wissen möchte sei auf diesen Beitrag verwiesen: Von Korrelationen, Trends bei Anomalien![5]
Doch diese Annahme ist – bei Zeitreihen von Anomalien – und das werde ich im Folgenden belegen, bis auf eine Ausnahme, immer falsch!

Anmerkung:

Der folgende Text ist einem Artikel entnommen, den ich am 7. Februar 2011 bei EIKE einstellte, und der am 23.11.2018 aktualisiert wurde.
In der Klimatologie werden zur Bestimmung des Referenzwertes, die errechneten Monatsmittel oder Jahresmittel der gemessenen Temperatur einer Station, über den Zeitraum von 1961 bis 1990 aufaddiert und durch die Anzahl aller Monats- oder Jahresmittel dieses Zeitraumes geteilt. Der so enthaltene Wert entspricht einer Geraden gleicher „Temperatur“ über den Referenz-Zeitraum von 1961 bis 1990. (Es kann im Prinzip aber auch jeder andere Zeitraum sein.) Der zugehörige Referenz-Wert wird oft das Stationsnormal genannt. Folgerichtig heißen die Abweichungen vom (Stations)-Normal Anomalien.
Nun bildet man die Differenz aus allen absoluten Jahresmitteln Tx der Zeitreihe und dem Stationsnormal Tref und ermittelt auf diese Weise eine neue Zeitreihe der Anomalien eben dieser Station.  Dabei geht man von der Annahme aus, dass diese, wenn sie einen Fehler C enthalten, dieser auch im Stationsnormal vorhanden ist. Ferner unterstellt man, dass C eine konstante Größe hat. Bspw. Brohan und Jones[6] formulieren diese Annahme (in Bezug auf die Fehler durch unterschiedliche Mittelwertbildung) so:
„..There will be a difference between the true mean monthly temperature (i.e. from 1 minuteaverages) and the average calculated by each station from measurements made less often; but this difference will also be present in the station normal and will cancel in the anomaly.
Berechnet man jetzt die Anomalie Ax = (Tx+C) –(Tref+ C), dann hebt sich C auf. Das ist schlichte Algebra. So weit so gut! Die große Frage ist nun, funktioniert das bei Zeitreihen auch so? Warum denn nicht, wird mancher vorschnell antworten. Die Algebra ist schließlich immer gleich! Oder?
Es zeigt sich sehr schnell, dass die Idee der Fehlerkompensation, die hinter dieser einfachen Methode steckt, ebenso plausibel wie falsch ist, bzw. sie stimmt nur innerhalb ganz enger Randbedingungen, die in der hier interessierenden Praxis nicht eintreten.
Ende Teil 2
[1] Zitate in deutscher Übersetzung von Pat Frank Quelle: https://www.eike-klima-energie.eu/2019/09/09/fehler-fortpflanzung-und-die-zuverlaessigkeit-von-projektionen-der-globalen-lufttemperatur/
[2] Brohan, PK,J. J. Harris, I., Tett S. F. B.; & Jones, P. D. (2006) Uncertainty estimates in regional and global observed temperature changes: a new dataset from 1850. HadCRUT 3 HadCRUT 3:1 to 35.
[3] Brohan et. al geben auf Seite 6 den allgemeinen Glauben an die Fehlerfreiheit der Anomalien wider, in dem sie schreiben: „..There will be a difference between the true mean monthly temperature (i.e. from 1 minute averages) and the average calculated by each station from measurements made less often; but this difference will also be present in the station normal and will cancel in the anomaly. So this doesn’t contribute to the measurement error.“ Im Folgenden beschreiben die Autoren wie die Anforderungen an die Bildung der „station normals“ also der Referenzewerte (lt. WMO der Mittelwert jeder Station über die Jahre 1961-1990) aufgeweicht (relaxed) wurden. Die durchgeführte Re­duk­ti­on der An­for­de­run­gen zur Bildung des Referenzwertes (Station Normal) auf nur noch 15 Jah­re und da­raus 3 x 4 Jah­re in je­der De­ka­de, er­höht den Feh­ler, der schon in der Ver­wen­dung des Sta­ti­on Nor­mals steckt, wei­ter.
[4] Verwirrspiel um die absolute globale Mitteltemperatur Verwirrspiel um die absolute globale Mitteltemperatur
[5] https://www.eike-klima-energie.eu/2018/01/09/von-korrelationen-trends-bei-anomalien/
[6] Brohan, PK,J. J. Harris, I., Tett S. F. B.; & Jones, P. D. (2006) Uncertainty estimates in regional and global observed temperature changes: a new dataset from 1850. HadCRUT 3 HadCRUT 3:1 to 35.
Für alle die diese Arbeit am Stück lesen wollen hier das pdf dazu Die schwierige nimmer endende Fehlerdiskussion