Unsicherheit beenden: Zufallsstichproben testen!

CoViD-19 hat die Welt im Griff. Viele Länder, auch Deutschland, befinden sich im Lockdown. In Italien, England und USA wird die Kapazität der Krankenhäuser knapp oder ist schon überschritten. In Deutschland fehlt Schutzkleidung. Gleichzeitig geraten immer mehr Unternehmen und Selbstständige in existentielle Not. Alle fragen sich: Wie lange wird der Stillstand des öffentlichen Lebens andauern? Wie viele Opfer wird die Pandemie fordern, direkt und indirekt? Während die einen größere Angst vor dem Virus haben, fürchten die anderen mehr die Nebenwirkungen der staatlichen Maßnahmen: Rezession oder gar Depression der Wirtschaft, psychosoziale Überlastung der Bevölkerung, Einschränkung von Grundrechten, Vernachlässigung anderer Erkrankungen. Die allabendlichen Nachrichtensendungen liefern für alle diese Punkte anschauliche Beispiele.

Bei der Suche nach dem optimalen Weg durch die Krise starren alle gebannt auf die jeweils neuesten Statistiken. Wir wollen wissen:

1. Welcher Anteil der Bevölkerung infiziert sich in welcher Zeit,
   a) ohne und b) mit Eindämmungsmaßnahmen?
2. Welcher Anteil der Infizierten wird nicht krank, leicht krank, schwerkrank, intensivpflichtig, stirbt?

Allerdings hat sich in den Medien inzwischen auch herumgesprochen, dass die veröffentlichten Statistiken über die Gefährlichkeit des neuen Virus sehr wenig aussagen. Umgekehrt kämen Maßnahmen, die sich an reinen Sterbezahlen orientieren, zu spät. Es gibt einfach zu viele Unbekannte, nämlich:

 

1. Welcher Anteil der Bevölkerung wird getestet, und wie selektiv ist diese Testpopulation?

Während in Italien offenbar Patienten erst dann getestet werden, wenn sie ins Krankenhaus aufgenommen werden, genügt in Deutschland ein „Verdacht“, definiert als Kontakt mit einem nachgewiesen Infizierten oder Aufenthalt in einem definierten Risikogebiet. Menschen mit auffälligen Symptomen werden hingegen auch bei uns nicht getestet, Menschen mit symptomarmen Verläufen überhaupt nicht. Insofern weiß niemand, wie viele Infizierte auf einen positiv Getesteten kommen. Schätzungen der Dunkelziffer reichen von 3-4 bis über 1000.

Wenn man nicht nur „Verdachtsfälle“ oder Schwerkranke, sondern Zufallsstichproben testen würde, könnte man die Dunkelziffer schätzen.  

 

2. Wie zuverlässig ist der Test?

Ist jemand, der positiv getestet wurde, wirklich infiziert?

Prinzipiell können bei Virusinfektionen zwei Typen von Tests eingesetzt werden: Nachweis von Viren, bei SARS-CoV-2 aus einem Halsabstrich (PCR-Methode), und Nachweis von Antikörpern, bei SARS-CoV-2. Letzter scheint kurz vor der Verfügbarkeit zu stehen und soll bereits in einer New Yorker Klinik eingesetzt werden (hier). Ersterer soll akute Infektionen nachweisen, letzterer durchgemachte (und damit hoffentlich Immunität).

Der PCR-Test ist nicht validiert. Der Anteil der positiv Getesteten, die wirklich mit SARS-CoV-2 infiziert sind, berechnet sich nach dem Satz von Bayes. Dazu benötigt man die Sensitivität (Anteil korrekt Positiver = 1 – Anteil falsch Negativer) und Spezifität des Tests (Anteil korrekt Negativer = 1 – Anteil falsch Positiver) sowie die Basisrate (Anteil Infizierter in der Testpopulation).

Der Anteil an Infizierten AI unter den positiv Getesteten beträgt mit S = Sensitivität, Sp = Spezifität und B = Basisrate):

AI = (S + B) / [ (S x B + (1 -Sp) x (1 – B) ]

Für den PCR-Test werden in der bislang sehr spärlichen Literatur Falsch-Positiv-Raten zwischen 0 % und 80 % gehandelt, die Basisrate ist nicht bekannt. Hier einige fiktive Rechenbeispiele (alle Angaben in %):

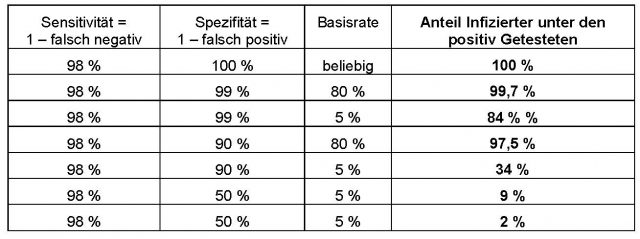
Der Test ist also bei hoher Basisrate recht zuverlässig, bei niedriger nicht. Das könnte erklären, warum in Deutschland gegenüber Italien so viel mehr positiv Getestete auf Verstorbene kommen: Vermutlich ist in Italien in der Testpopulation (krankenhauspflichtige Lungenentzündung) die Basisrate um ein Vielfaches höher als in Deutschland („Verdachtsfälle“, s.o.). Man liest oft, in Italien sei die Dunkelziffer höher als in Deutschland. Vielleicht ist in Deutschland zusätzlich aber auch die „Hellziffer“ höher, d.h. es gibt positiv Getestete, die gar nicht infiziert sind.

Die Zuverlässigkeit des Tests hängt gerade bei kleiner Basisrate sehr stark von der Spezifität bzw. Rate der falsch Positiven ab. Wenn diese nicht bekannt ist, kann man in den Satz von Bayes ganz einfach den Anteil der positiv Getesteten aus der Population einsetzen:

Der Anteil Infizierter AP unter den positiv Getesteten (S = Sensitivität, B = Basisrate) ist

AP = ( S x B ) / ( Anteil positiverTests )

 

Der Anteil positiver Tests ist leicht anhand einer Zufallsstichprobe zu  schätzen!  

Die Statistikerin Katharina Schüller hat wesentliche Probleme der bisherigen Corona-Statistiken anschaulich in einem Fokus-Artikel beschrieben und fordert regelmäßige Tests an Zufallsstichproben, um die Mängel zu beheben. Von Seiten der Medizin wird regelmäßig auf solche Forderungen geantwortet: Die Labore sind ausgelastet, dafür haben wir keine Kapazität.

Aber macht es angesichts von mehr als 50.000 „bestätigten“ Fällen in Deutschland und einer parallel verhängten Kontaktsperre für alle noch Sinn, jeden einzelnen „Verdachtsfall“ (ich erinnere, Verdachtsfall wird man nicht durch Erkrankung, sondern ausschließlich durch Kontakt mit einem positiv Getesteten oder Aufenthalt in Risikogebiet) unter Quarantäne zu stellen und zu beobachten? Wäre es nicht zielführender, die vorhandene Testkapazität aufzuteilen auf a) Patienten mit erheblichen klinischen Symptomen, und b) Zufallsstichproben? Die Zufallsstichproben müssten (per einfacher Änderung des Infektionsschutzgesetzes) aus der Einwohnermeldedatei gezogen, regelmäßig getestet und klinisch beobachtet werden, um Schätzungen für die vielen Unbekannten zu erhalten.

Eine einfache Rechnung zeigt, dass bereits einer Zufallsstichprobe von 400 Personen beispielsweise eine Rate von 5 % auf +/- 2 % genau geschätzt werden kann, und mit 2000 Personen auf +/- 1 % genau. Das würde uns schon viel weiterhelfen.

Hier können Sie eine Petition an die Bundesregierung unterzeichnen, die Tests an Zufallsstichproben fordert.