Verbesserungswürdig: Über fehlerhafte Ansätze für eine breitenabhängige Globaltemperatur
Zitat:
“Here’s how the incident solar flux changes with time-of-day and latitude. This should not be controversial, since it is just based upon geometry. Even though I only do model calculations at latitudes of 5, 15, 25, 35, 45, 55, 65, 75, and 85 deg. (north and south), the global, 24-hr average incident solar flux is very close to simply 1,370 divided by 4, which is the ratio of the surface areas of a circle and a sphere having the same radius…”
Der neutrale GOOGLE-Übersetzer sagt: Hier erfahren Sie, wie sich der einfallende Sonnenfluss mit der Tageszeit und dem Breitengrad ändert. Dies sollte nicht kontrovers sein, da es nur auf Geometrie basiert. Obwohl ich nur Modellberechnungen in Breiten von 5, 15, 25, 35, 45, 55, 65, 75 und 85 Grad mache. (Nord und Süd) liegt der globale, durchschnittlich einfallende Sonnenfluss von 24 Stunden sehr nahe bei 1.370 geteilt durch 4, was dem Verhältnis der Oberflächen eines Kreises und einer Kugel mit demselben Radius entspricht…
Die Ableitung einer breitenabhängigen Tagestemperatur wäre tatsächlich ein guter Anfang für ein hemisphärisches Tag&Nacht-Verständnis gewesen, aber der Rückfall auf einen speichergestützten 24h-Verlauf zerstört diesen Ansatz sofort wieder, wie die nachfolgenden Abbildungen von Dr. Spencer nachweisen:
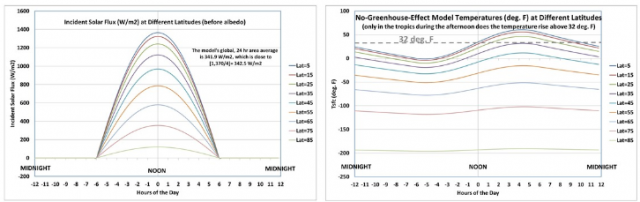
Abbildungen aus “A Simple ‘No Greenhouse Effect’ Model of Day/Night Temperatures at Different Latitudes“ von Dr. Roy Spencer Links: Einfallende solare Strahlungsleistung von 5° bis 85° geographischer Breite Rechts: 24h-Temperaturverlauf: Im Tagesverlauf wird eingestrahlte Energie über einen speicherfähigen „surface layer responding to heating“ von 0.1 m Tiefe abgezweigt und dem nächtlichen Temperaturverlauf zugerechnet
Das von Dr. Spencer vorgestellte Modell stellt implizit den Temperaturverlauf einer breitenabhängigen Strahlungsbilanz gegen eine Umgebungstemperatur von 0 Kelvin dar, dessen pauschale „Mittelerde“-Anwendung im konventionellen Stefan-Boltzmann-Ansatz zu einer theoretischen Globaltemperatur von (-18°C) führt. Eine breitenabhängige Berechnung der solaren Strahlungsleistung und eine Vorratsspeicherung für die Nachtstunden führt in dem Modell von Dr. Spencer dann zu einer Spreizung der Temperaturen zwischen etwa 60°F (=15,55°C) und etwa -100°F (= -73,33°C). Insbesondere kann Dr. Spencer damit aber die Temperaturgenese auf unserer Erde nicht korrekt erklären, Zitat letzter Absatz aus diesem Artikel:
“I hope this will help convince some who are still open-minded on this subject that even intense tropical sunshine cannot explain real-world tropical temperatures. The atmospheric greenhouse effect must also be included. The temperature (of anything) is not determined by the rate of energy input (say, the intensity of sunlight, or how fast your car engine burns gas); it is the result of a balance between energy gain and energy loss. The greenhouse effect reduces the rate of energy loss at the surface, thus causing higher temperatures then if it did not exist.”
Der neutrale GOOGLE-Übersetzer sagt: Ich hoffe, dies wird dazu beitragen, einige, die in diesem Bereich noch aufgeschlossen sind, davon zu überzeugen, dass selbst intensiver tropischer Sonnenschein die realen tropischen Temperaturen nicht erklären kann. Der atmosphärische Treibhauseffekt muss ebenfalls berücksichtigt werden. Die Temperatur (von irgendetwas) wird nicht durch die Energieeintragsrate bestimmt (z. B. die Intensität des Sonnenlichts oder wie schnell Ihr Automotor Gas verbrennt); Es ist das Ergebnis eines Gleichgewichts zwischen Energiegewinn und Energieverlust. Der Treibhauseffekt verringert die Energieverlustrate an der Oberfläche und verursacht somit höhere Temperaturen als wenn sie nicht vorhanden wären.
Schade, da hatte Dr. Roy Spencer die breitenabhängige spezifische solare Strahlungsleistung richtig berechnet. Aber anstatt daraus den gleichzeitigen Verlauf einer S-B-Gleichgewichtstemperatur abzuleiten und mit der Realität abzugleichen, negiert er diese zwingende Gleichzeitigkeit aus dem S-B-Gesetz und leitet aus seinem Speichermodell die Vermutung für einen „isolierenden“ atmosphärischen THE ab. Das Problem bei diesem THE ist nur, dass noch niemals irgendein Körper ohne zusätzliche Energiezufuhr allein durch eine Behinderung seines Energieverlustes WÄRMER geworden ist. Ein solcher Körper wird durch Isolation nämlich nicht WÄRMER, sondern kühlt nur entsprechend LANGSAMER aus. Und die spezifische solare Strahlungsleistung bei vertikalem Einfall, wie sie von Dr. Spencer richtig dargestellt worden war, beträgt zwischen den Wendekreisen ohne Albedo maximal (S0=1.367W/m²) und entspricht einer S-B-Gleichgewichtstemperatur von etwa 120°C – und kann daher sehr wohl die Temperatur in den Tropen erklären.
Dr. Spencer bleibt ausgerechnet die Erklärung schuldig, warum er in seinem Modell die zwingende Gleichzeitigkeit zwischen Temperatur und spezifischer Strahlungsleistung aus dem Stefan-Boltzmann-Gesetz aufhebt und einen wesentlichen Teil der tagseitigen hemisphärischen Strahlungsleistung willkürlich auf die Nachtstunden umleitet.
Die Berechnungen von Dr. Spencer wurden aus Vereinfachungsgründen im Äquinoktium durchgeführt. Aus der spezifischen solaren Strahlungsleistung werden aber hin und wieder auch breitenabhängige tagesdurchschnittliche „spezifische“ 24h-„Mittelerde“-Strahlungsleistungen für den gesamten Jahresverlauf abgeleitet:
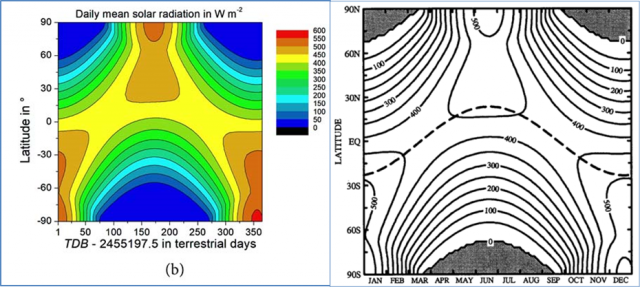
Abbildung: 24h-gemittelte tägliche „spezifische“ Strahlungsleistung der Sonne in Abhängigkeit von der Jahreszeit und der geographischen Breite über ein Jahr Links: Abbildung 22b „solar radiation reaching the Earth’s surface“ aus Kramm et al. (2017) „Using Earth’s Moon as a Testbed for Quantifying the Effect of the Terrestrial Atmosphere” (Creative Commons License CC BY 4.0) Rechts: Abbildung 2.6 von Dennis L. Hartmann für die Außengrenze der Atmosphäre aus “Global Physical Climatology”, Chapter 2 Volume 56 in the INTERNATIONAL GEOPHYSICS SERIES, ACADEMIC PRESS 1994
Bis auf eine fehlende Darstellung der „0W/m²“-Linie auf den Polkappen bei Kramm et al. (2017) erscheinen beide Darstellungen zunächst einmal völlig gleich. Die unterschiedlichen Werte für die Maximaleinstrahlung am Pol der jeweiligen Sommerhemisphäre zeigen sogar, dass in beide Berechnungen die Elliptizität der Erdbahn eingegangen ist. In beiden Graphiken fallen am Nordpol über 500 W/m² und am Südpol über 550 W/m² an; denn der Südsommer fällt auf die sonnennahe Seite der Erdbahn (Perihel), während die Sonne im Nordsommer auf deren entfernter Seite (Abhel) steht. Die Übereinstimmung beider Abbildungen ist aber insofern höchst verwunderlich, weil Kramm et al. (2017) eindeutig von „solar radiation reaching the Earth’s surface“ sprechen, während Dennis L. Hartmann (1994) die „Mittlere tägliche Einstrahlung an der Außengrenze der Atmosphäre“ darstellt. Schließlich machen zwischen der Außengrenze der Atmosphäre und der Erdoberfläche die Wolken bereits etwa 70 Prozent der Erd-Albedo von etwa 0,3 aus, und eine dauerhafte Eisbedeckung dürfte sich eher positiv auf die örtliche Albedo auswirken. Ohne den verantwortlichen Lead-Autor unnötig in Aufregung versetzen zu wollen, sollten sich Kramm et al. ihre Abbildung 22b also unbedingt noch einmal genauer anschauen; denn hier wäre dringend ein wissenschaftliches Korrigendum anzuraten.
Tatsächlich ist in beiden oben abgebildeten Graphiken von Kramm et al. (2017) und Dennis L. Hartmann (1994) der Jahresverlauf für die beiden Pole auf +/-90° nördlicher und südlicher geographischer Breite richtig; denn hier kann die spezifische Strahlungsleistung über den 24h-Tag als konstant angesehen werden. Alle anderen Verläufe stellen über 24 Stunden gemittelte Strahlungswerte dar, die umso weniger mit einer originären spezifischen Strahlungsleistung der Sonne zu tun haben, je weiter sich die betreffende Ortslage von einem der geographischen Pole entfernt. Solche gemittelten Strahlungswerte stellen keine originäre spezifische Strahlungsleistung dar und dürfen daher auch nicht mit dem Stefan-Boltzmann-Gesetz in ein Temperaturäquivalent umgerechnet werden. Trotzdem wird manchmal ein solcher Durchschnitt fälschlich in eine S-B-Gleichgewichtstemperatur umgerechnet. In der Veröffentlichung „Using Earth’s Moon as a Testbed for Quantifying the Effect of the Terrestrial Atmosphere” von Gerhard Kramm et al. (2017) finden wir in Abbildung 22a eine solche Darstellung:
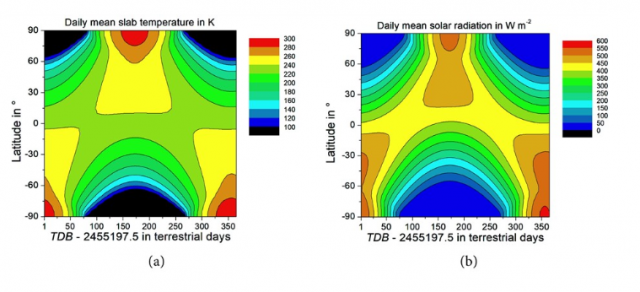
Abbildungen 22 a und b aus Kramm et al. (2017)
Beschreibung: “Daily mean values of (a) slab temperature; (b) solar radiation reaching the Earth’s surface; … as predicted for one year starting with TDB=2,455,197.5 (January 1, 2010, 00:00 UT1).”
(Creative Commons License CC BY 4.0)
Anmerkung: Die maximale spezifische Strahlungsleistung unter dem Zenitwinkel von 66,6° zur Sommersonnenwende am jeweiligen Pol der Sommerhemisphäre (abgeleitet von der Solarkonstanten S0=1.367W/m² ohne Erdbahn-Elliptizität) beträgt:
Maximale spez. Strahlungsleistung am Sommerpol ohne Albedo: 544 W/m², entsprechend einer S-B-Gleichgewichtstemperatur von 40°C oder 313K.
Maximale spez. Strahlungsleistung am Sommerpol bei mittlerer Albedo: 374 W/m², entsprechend einer S-B-Gleichgewichtstemperatur von 12°C oder 285K.
In der Abbildung 22a von Kramm et al. (2017) weist die rote Farbgebung nun eine Maximaltemperatur zwischen 280K und 300K für den jeweiligen Pol der Sommerhemisphäre aus. Diese Temperaturspanne entspricht jedoch nicht der entsprechenden spezifischen Strahlungsleistung aus Abbildung 22b mit mehr als 500W/m² (Nordpol) respektive mehr als 550W/m² (Südpol). Denn damit müssten die Ortstemperaturen an den Polen der Sommerhemisphäre in Abbildung 22a deutlich mehr als 300K betragen. Daher können die Temperaturen in Abbildung 22a eindeutig nicht aus den Strahlungswerten von Abbildung 22b hergeleitet worden sein. Sicherlich wird der verantwortliche Lead-Autor diesen Widerspruch mit dem ihm eigenen Charme durch eine plausible physikalische Erklärung auflösen können, die seinen hohen wissenschaftlichen Ansprüchen gerecht wird. Bis dahin bleibt nur der hinreichende Verdacht, dass beim Datensatz für die Strahlungsleistung in Abbildung 22b eine Verwechslung mit den Grunddaten @TOA vorliegen muss.
In Teil 2 meiner Analyse der Thesen und Antithesen für einen natürlichen atmosphärischen Treibhauseffekt hatte ich zu der Abbildung 22a von Kramm et al. (2017) angemerkt, Zitat:
„Kramm et al. (2017) stellen in Abbildung 22 den breitenabhängigen 24-Stunden-Durchschnitt der solaren Einstrahlung und dessen S-B-Temperaturäquivalent dar. Die Problematik einer solchen 24-stundendurchschnittlichen solaren Strahlungsleistung hatte ich in meinem EIKE-Artikel „Noch ein paar Fragen zum ‚natürlichen‘ atmosphärischen Treibhauseffekt“ vom 23. Juni 2017 anhand einer vergleichbaren Abbildung von Dennis L. Hartmann ausführlich erläutert; insbesondere lässt ein solcher Strahlungsdurchschnitt keinesfalls die Berechnung eines S-B-Temperaturäquivalentes zu…“
Es handelt sich bei den dargestellten Werten also gar nicht um physikalisch korrekte spezifische Strahlungsleistungen, aus denen sich mittels Stefan-Boltzmann-Gesetz eine rechnerische Gleichgewichtstemperatur ermitteln ließe, sondern nur um mathematisch berechnete 24h-Mittelwerte. Zur Ermittlung eines globalen Jahresverlaufs des maximalen S-B-Temperaturäquivalentes müssen wir vielmehr das breitenabhängige Maximum der spezifischen solaren Strahlungsleistung betrachten:
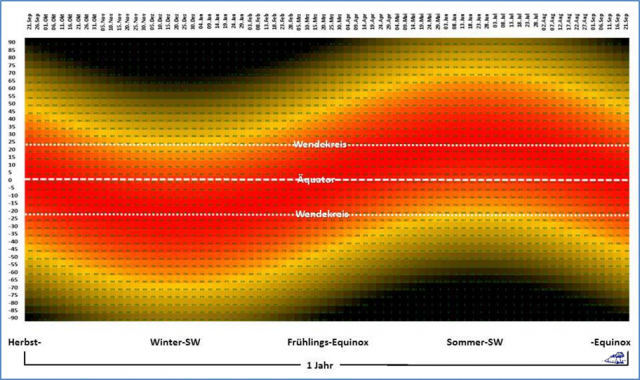
Abbildung: Das örtliche Maximum der breitenabhängigen temperaturwirksamen spezifischen Strahlungsleistung der Sonne für die gesamte Erde über ein volles Jahr von Herbstäquinoktium zu Herbstäquinoktium
Spez. Strahlungsleistung: MAX (Si) @24h-Tag mit (Si = 1.367W/m² * (1-ALBEDO) * cos PHIi)
und (PHIi = örtlicher Zenitwinkel)
Farbdarstellung: 0 [W/m²] (schwarz) – 940 [W/m²] (rot)
Linke Skala: Grad geographische Breite (Süd = „-“)
Skala oben: Datum ab Herbstäquinoktium
Anmerkung: Ein vergleichbarer geographischer Verlauf ergibt sich ebenfalls für das daraus abgeleitete S-B-Temperaturäquivalent (SBT) zwischen (-273°C=schwarz) und (86°C=rot)
Dabei übertrifft das temperaturwirksame solare Sommermaximum am Nordpol (374 W/m² @ 90°N) sogar das solare Winterminimum in unseren Breiten (270 W/m² @ 50°N). Umgekehrt ist aber die maximale solare Sommereinstrahlung in unseren Breiten in etwa mit der Sonneneinstrahlung am nördlichen Wendekreis bei äquatorialem Sonnenstand vergleichbar.
Damit fällt der jeweilige Pol der Sommerhemisphäre als klimatischer „Hotspot“ schon mal aus, wie die nachstehende Abbildung beweist:
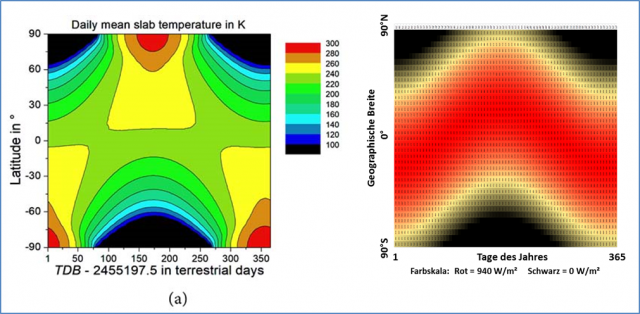
Abbildung: Vergleich der „Daily mean values of (a) slab temperature” von Kramm et al. (2017) – Creative Commons License CC BY 4.0 (links) mit dem Jahresverlauf des örtlichen Maximums der breitenabhängigen temperaturwirksamen spezifischen Strahlungsleistung der Sonne (rechts)
Deutlich wird aus dieser Abbildung, dass die Temperaturen von Kramm et al. (2017) niemals aus einer breitenabhängigen maximalen spezifischen Strahlungsleistung der Sonne abgeleitet worden sein können. Also ist der jeweilige Pol der Sommerhemisphäre mit einer maximalen temperaturwirksamen spezifischen Strahlungsleistung von 374 W/m² und einer S-B-Gleichgewichtstemperatur von 12°C auch kein klimatischer „Hotspot“. Vielmehr verläuft die maximale temperaturwirksame spezifische Strahlungsleistung von 940 W/m² mit einem S-B-Temperaturäquivalent von 86°C am Fußpunkt des jahreszeitlich veränderlichen vertikalen Sonnenstandes zwischen den geographischen Breitenkreisen, was die nachfolgende Abbildung nochmals verdeutlicht:
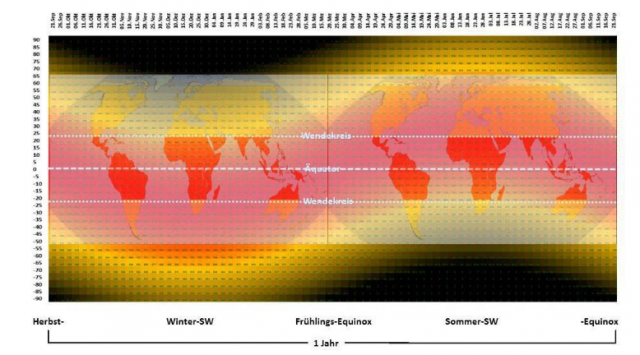
Abbildung: Tentative Gegenüberstellung der Beleuchtungsklimazonen mit dem Jahresverlauf der maximalen solaren Strahlungsleistung im Sommerhalbjahr (Südsommer linke Hälfte und Nordsommer rechte Hälfte) Overlays rechts und links: Die Beleuchtungsklimazonen der Erde: von oben/unten zur Mitte: Polarzonen, Mittelbreiten, Tropenzone (Quelle: Wikipedia, Autor: Fährtenleser, Lizenz: GNU Free Documentation License) Darunter: Das örtliche Maximum der breitenabhängigen temperaturwirksamen spezifischen Strahlungsleistung der Sonne für die gesamte Erde über ein volles Jahr von Herbstäquinoktium zu Herbstäquinoktium
Aus der vorstehenden Abbildung ist klar ersichtlich, dass aus den Strahlungs-Hotspots auf der Polkalotte der jeweiligen Sommerhemisphäre nach Kramm et al. (2017) und Dennis L. Hartmann (1994) kein entsprechender Klima-Hotspot resultieren kann. Auch ein „Temperatur-Hotspot“ analog zu Kramm et al. (2017) ist aus dem Abgleich zwischen Beleuchtungsklimazonen und dem Jahresverlauf der maximalen solaren Strahlungsleistung im arktischen und antarktischen Hochsommer beim besten Willen nicht zu erkennen. Die Polkalotten werden vielmehr eindeutig der solaren Polarzone mit extremen jahreszeitlichen Schwankungen der Tageslänge und der Sonneneinstrahlung zugeordnet. Und das absolute Maximum der spezifischen solaren Strahlungsleistung liegt immer noch zwischen den geographischen Wendekreisen. Die polaren Strahlungs-Hotspots sind bei einem 24h-Durchschnitt vielmehr der örtlichen Tageslänge auf der jeweiligen Sommerhemisphäre und damit der längeren Einstrahlungsdauer geschuldet. Umgekehrt wird bei einem 24h-Durchschnitt das Maximum der breitenabhängigen temperaturwirksamen spezifischen solaren Strahlungsleistung in der Äquatorregion aufgrund der wesentlich kürzeren Tageslänge zwischen Sonnenauf- und -untergang auf weniger als die Hälfte reduziert, obwohl diese Region nachweislich den „Klimamotor“ unserer Erde antreibt.
Der Vollständigkeit halber sei abschließend noch darauf hingewiesen, dass die Sonnenscheindauer in höheren geographischen Breiten der Sommerhemisphäre aufgrund der Albedo-Rückkopplung eine wesentliche Rolle bei der langfristigen Klimaentwicklung spielt, wie das bereits Köppen und Wegener in ihrem Buch „Die Klimate der geologischen Vorzeit“ (Bornträger 1924) gezeigt hatten. Eine einfache Hypothese für eine solche Albedo-Rückkopplung wird hier beschrieben.