Die Mathematik von Epidemien
Wir hören derzeit viel über „exponentielles Wachstum“ hinsichtlich Anzahl der Fälle, Verbreitung und Sterberate des Corona-Virus‘. Und es handelt sich ja wirklich um eine globale Gesundheits-Krise, die man sehr ernst nehmen muss.
Komisch dabei ist aber, dass der Terminus „exponentielles Wachstum“ nicht wirklich das Fortschreiten einer gegebenen Krankheit beschreibt. Exponentielles Wachstum hört niemals auf – es wird nur größer und immer größer. Aber im Falle einer Krankheit ist das nicht der Fall.
Als Beleg sei hier beispielhaft die Anzahl der Corona-Virus-Erkrankungen in Südkorea gezeigt:
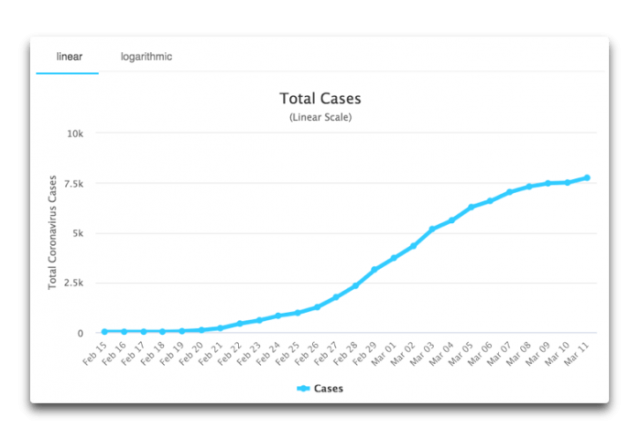
Abbildung 1: Gesamtzahl der Coronavirus-Fälle seit Beginn der Epidemie. Quelle
Die Kurve der Anzahl der Todesfälle in China hat die gleiche Form:
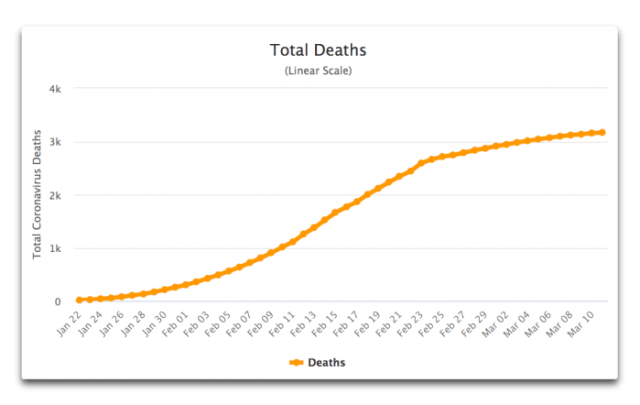
Abbildung 2: Gesamtzahl der Todesfälle durch das Corona-Virus in China seit Ausbruch der Krankheit. Quelle
Diese spezielle „S-förmige“ Kurve wird eine „Gompertz-Kurve“ genannt. Sie ist seltsam, da nicht symmetrisch. Der Anstieg erfolgt schneller als die Abschwächung. Ein Beispiel:
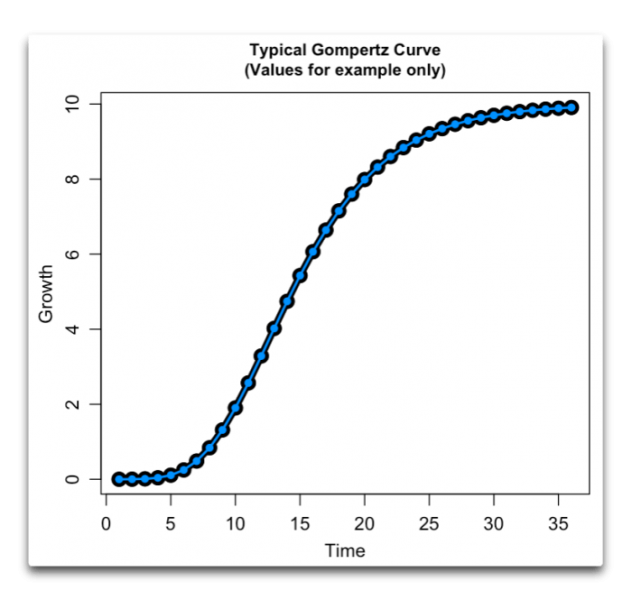
Abbildung 3: Eine typische Gompertz-Kurve, welche die Entwicklung der Anzahl der Gesamtfälle oder die Gesamtzahl der Todesfälle während einer Epidemie zeigt.
Nun wollte ich einmal nachschauen, wie gut die Graphiken der Abbildungen 1 und 2 in eine Gompertz-Kurve eingepasst werden können. Zunächst folgt hier der Verlauf der Gesamtfälle in Südkorea, zusammen mit dem Best Fit einer Gompertz-Kurve:
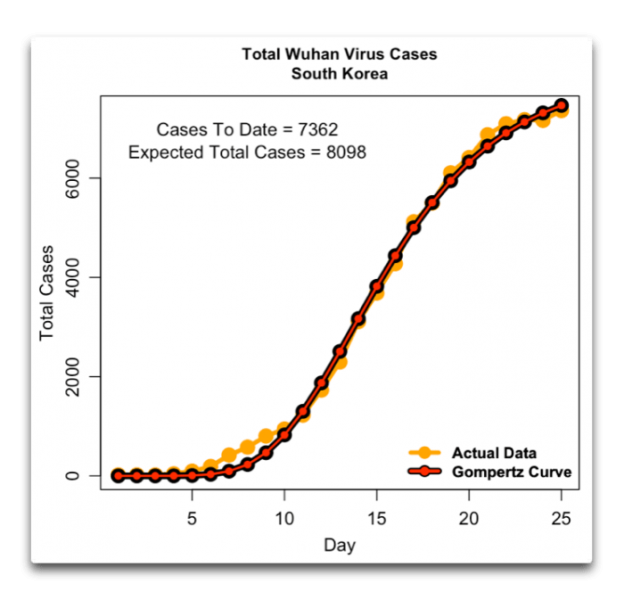
Abbildung 4: Gesamtzahl der Corona-Fälle in Südkorea, zusammen mit der Best Fit-Gompertz-Kurve für die Daten.
Man erkennt, warum man die Gompertz-Kurve nutzt, um Epidemien zu beschreiben – sie passt sehr gut zu epidemiologischen Daten der realen Welt. Und weil jedwede gegebene Gompertz-Kurve bei irgendeinem Maximalwert endet, ohne diesen zu überschreiten, lässt sich damit auch der Teil der Kurve abschätzen, zu dem es bisher noch nicht gekommen ist. Bislang waren in Südkorea 7362 Fälle aufgetreten. Der Schätzung der Gompertz-Kurve nach dürfte sich die schlussendliche Gesamtzahl bei 8100 Fällen oder so einpendeln.
Nun ist das natürlich keine besonders große Zahl. Alles Mögliche kann passieren, damit die Kurve entweder auf- oder abwärts zu laufen beginnt. Aber es ist immer noch besser als die Schätzung nach der Pi-mal-Daumen-Methode.
Als Nächstes folgt hier die gleiche Darstellung, Daten plus Best Fit einer Gompertz-Kurve, aber diesmal der Todesfälle in China:
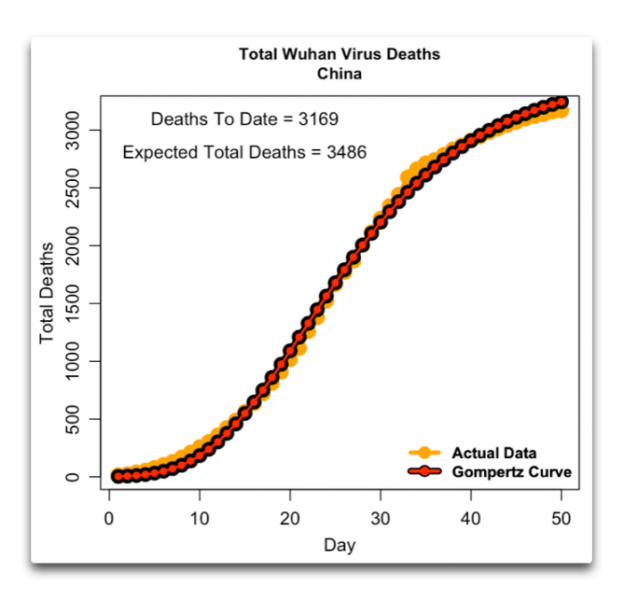
Abbildung 5: Gesamtzahl der Todesfälle durch das Corona-Virus in China, zusammen mit einer Best Fit-Gompertz-Kurve der Daten.
Auch hier können wir unter Berücksichtigung der eben erwähnten Schwächen eine geeignete Abschätzung vornehmen, welche Gesamtzahl an Todesfällen auftreten wird. Zum Ende ergibt sich laut Gompertz-Kurve eine Schätzung von etwa 3500 Todesfällen.
Zum Schluss noch ein Blick auf Südkorea. Dort treten immer noch Todesfälle auf, so dass diese Schätzung unsicherer ist:
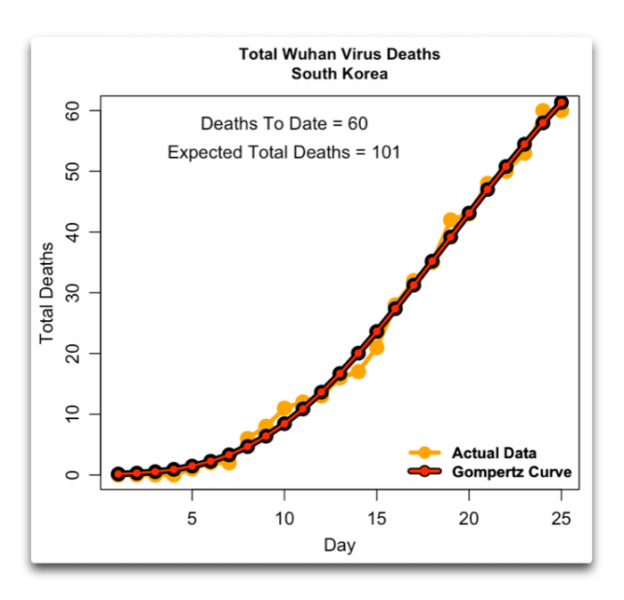
Abbildung 6: Gesamtzahl der Todesfälle durch das Corona-Virus, wieder mit dem Best Fit einer Gompertz-Kurve für die Daten.
Obwohl die Unsicherheit hier größer ist, sieht es gegenwärtig so aus, dass sich die letztendliche Gesamtzahl der Todesfälle in Südkorea größenordnungsmäßig auf 100 ergeben wird.
Schlussfolgerungen
Zumindest auf meinem Planeten sind das sehr gute Nachrichten. Es sieht so aus, als ob die Todesfälle in China in der Größenordnung von 3500 liegt. Die Fälle in Südkorea befinden sich dicht vor dem Maximum. Und obwohl es vermutlich noch zu früh ist, Schätzungen für Südkorea vorzunehmen, gab es dort bisher nur 60 Todesopfer, und das Best Fit der Gompertz-Kurve ergibt etwa 100 Todesfälle.
Bitte nicht glauben, dass ich die Gefahr minimieren will. Ein Virus dieser Art kann gewaltige Schäden anrichten, wenn wir nicht dagegen vorgehen. Ich möchte hiermit aber sagen, dass China und Südkorea zeigen, dass wir dagegen vorgehen können.
Also schlage ich vor: Folgen wir allen Empfehlungen der Vorsorge wie Hände waschen, sozial Abstand nehmen, große Versammlungen absagen, Tests, Selbst-Quarantäne usw. Es ist sehr wichtig, die Ausbreitung des Virus‘ zu verlangsamen … und genauso wichtig, dass wir die Hysterie und die Politisierung dieses Vorgangs zurückschrauben. Ich versichere, die Verantwortung dafür einer politischen Partei in die Schuhe zu schieben oder Massen an Toilettenpapier zu kaufen wird nicht helfen, die Epidemie zu beenden. Dank Internet weiß ich, warum gerade Toilettenpapier … wenn jemand niest, verschmutzen 100 Menschen ihre Unterhosen … seien Sie keiner davon.
Daten: Alle Daten stammen von der Worldometer site.
Anhang: Eine Gompertz-Kurve ist definiert als:
y(t) = α * exp(-β * exp-(k*t))
wobei
t = time alpha = upper asymptote beta = growth displacement k = growth rate
…
[Hier folgt ein Anhang philosophischer Natur über den Begriff „rassistisch“, auch in Bezug auf andere Infektionskrankheiten. Weil das für die hier behandelte Thematik nebensächlich ist, wird auf das Original verwiesen. Anm. d. Übers.]
Link: https://wattsupwiththat.com/2020/03/13/the-math-of-epidemics/
Hier der oben angekündigte Bericht von
Coronavirus: Warum du jetzt handeln musst!
Du trägst Verantwortung in Politik, Gesellschaft oder Wirtschaft? Dann lies hier, was du wann tun musst.
Mit Dank an ACHGUT Autor Dr. med. Gunter Frank.