Zeigt der Poynting-Vektor auf „Mittelerde“ oder auf die sogenannte „Abstrahlungshöhe“?
Ist das nun die Haltung aller THE-Befürworter? – Nein, denn einer der THE-Befürworter hat vorgeblich dazugelernt, Zitat aus einem Kommentar vom 28. Dezember 2019 um 16:47 Uhr:
„Nein Herr Schulz, 30 Grad kommen heraus wenn die Hemisphäre als isotherm angenommen wird. Gerlich und Tscheuschner haben aber über cos exakt integriert und 15 Grad als Mittelwert herausbekommen. Sie haben nicht mal gespannt, dass Herr Weber zunächst – weil er die Nachtseite und damit den globalen Mittelwert von (288+0)/2=144 K nicht beachtet hat – wegen der rein solaren Temperaturgenese von 15 Grad (Tagseite, ohne Gegenstrahlung) behauptet hat, dass es keinen TE gibt. Später hat er dann die „Umgebungsgleichung“ für S-B sowie die angeblich verminderte Abstrahlung trotz 15 Grad erfunden und damit die fehlende Leistung für die Nachtseite herbeigezaubert.“
Nun, „dazugelernt“ war vielleicht nicht ganz der richtige Ausdruck, man könnte hier wohl zunächst von einer „sophistischen Schlagwortverwertung“ zugunsten des eigenen Paradigmas sprechen. Zu Gerlich und Tscheuschner (2009) hatte ich im 2. Teil meiner THE-Analyse konkret ausgeführt, Zitat:
„Der von Gerlich und Tscheuschner aufgezeigte Widerspruch (33°C # 144°C) ist analog zu dem gängigen „Faktor4“-Ansatz für einen „natürlichen atmosphärischen Treibhauseffekt“ innerhalb dieses Modells (1) korrekt abgeleitet worden.
Damit haben Gerlich&Tscheuschner den ‚natürlichen atmosphärischen Treibhauseffekt‘ widerlegt.
Allerdings ist diese Widerlegung aus dem global gemittelten Modell (1) heraus erfolgt und daher kann dieses Ergebnis nicht auf die reale Erde angewendet werden. Denn lediglich die Tagseite der Erde (2PIR2) darf im Strahlungsgleichgewicht zwischen Sonne und Erde mit dem Stefan-Boltzmann-Gesetz betrachtet werden. Von daher hätte diese Lösung von Gerlich and Tscheuschner (2009) auf die Tagseite der Erde (2PIR2) beschränkt bleiben müssen.“
Die besagten 15°C stammen nämlich aus meiner Reduzierung der Lösung von Gerlich und Tscheuschner auf die Tagseite der Erde als Beweis für meinen hemisphärischen S-B-Ansatz. Es bleibt demzufolge schleierhaft, worin der individuelle Erkenntnisgewinn des besagten THE-Befürworters bestehen mag, ob dieser lediglich etwas missverstanden haben könnte oder ob hier ausgewählte Teilaspekte willkürlich verwertet worden sind, um das widerlegte THE-Paradigma künstlich am Leben zu erhalten. Immerhin wird erkennbar, dass THE-Befürworter offenbar auch in der Lage sind, neue Erkenntnisse der Gegenseite wahrzunehmen. Wenn wir uns unter dieser Voraussetzung noch einmal dem widerlegten THE-Paradigma „von innen heraus“ nähern, dann gibt es vielleicht eine Möglichkeit, dessen Befürwortern ganz neue Erkenntnisse zu vermitteln, alsoschaunmermal:
Offenbar ist die Temperaturdifferenz von 33°C ein entscheidendes Argument für einen „natürlichen atmosphärischen Treibhauseffekt“, denn diese Differenz wird von allen THE-Befürwortern paternosterartig verbreitet; ein entsprechender Kommentar vom 25. Dezember 2019 um 14:16 Uhr lautet beispielsweise, Zitat mit Hervorhebungen:
„6. Zwischen den 14,8°C am Erdboden und -18,1°C, mit denen die Erde ihre Wärme ins All abstrahlt, besteht eine Differenz von 32,9°C. Also rund 33°C. Dies ist der natürliche THE und nicht die Differenz zwischen einer Erde mit und ohne THG.“
Und ein weiterer Kommentar vom 27. Dezember 2019 um 8:07 Uhr bestätigt diese Sichtweise, Zitat mit Hervorhebungen:
„Dann ergibt sich bei einer mittleren Einstrahlung über die gesamte Oberfläche von 239 W/m² (1364*0,7/4) an der Kugeloberfläche unterhalb der Beschichtung nach Stefan-Boltzmann eine Temperatur von fast 288 K. Nach aussen werden im Gleichgewicht aber statt 390 nur 239 W/m² abgestrahlt, was einer Schwarzkörpertemperatur von 255 K entspricht. Die Differenz sind 33 Grad, was als „Treibhauseffekt“ bezeichnet wird – selbst wenn der Vergleich mit einem Treibhaus nicht korrekt ist.“
Dieses THE-Paradigma stellt also das zweidimensionale Modell einer „Mittelerde“ dar und kann durch seine realitätswidrige Tag&Nacht-Mittelung der temperaturwirksamen solaren Einstrahlung bzw. dessen S-B-Temperaturäquivalentes charakterisiert werden, wie sie in Abbildung 1 dargestellt wird.
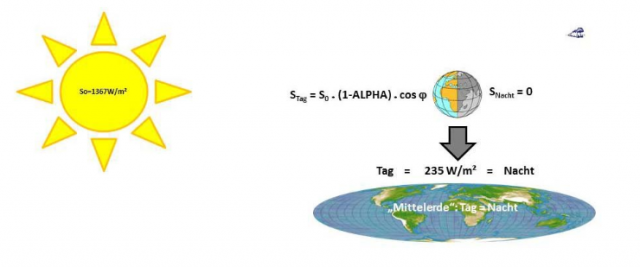
Abbildung 1: Das „Mittelerde“-Modell zur Erklärung eines „natürlichen atmosphärischen Treibhauseffektes“. Mit perspektivisch angepasster Mollweide-Projektion (Copyright L. Rohwedder – Lizenz CC BY-SA 3.0)
Nach diesem THE-„Mittelerde“-Modell betragen die Ein- und Ausstrahlung auf der Erde jeweils 235 W/m², während die angeblich gemessene globale Durchschnittstemperatur bei knapp 15°C liegt. Damit erhalten wir die in Abbildung 2 dargestellte Situation für die vorgeblich THE-bestimmenden 33°C im „Mittelerde“-Modell.
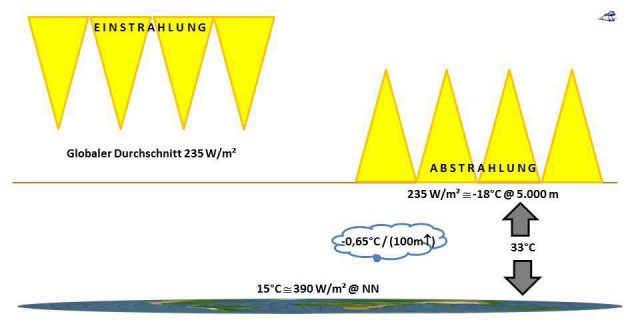
Abbildung 2: Durchschnittliche Ein- und Abstrahlung im „Mittelerde“-Modell mit den zugehörigen Durchschnittstemperaturen und der Temperaturdifferenz von 33°C Mit perspektivisch angepasster Mollweide-Projektion (Copyright L. Rohwedder – Lizenz CC BY-SA 3.0)
Dieses THE-„Mittelerde“-Modell kann, anders als mein hemisphärischer S-B-Ansatz, die gemessenen Temperaturen auf der Erde nicht erklären, und zwar völlig egal, ob es sich um einen angeblichen Durchschnitt oder individuelle Meßwerte handelt. Vielmehr wird zur Erklärung der gemessenen Individualtemperaturen oder irgendeines Durchschnittswertes im „Mittelerde“-Modell immer eine Temperaturdifferenz von 33°C mitgeschleppt, die wiederum mit einem „natürlichen atmosphärischen Treibhauseffekt“ erklärt wird. Die Abstrahlung der Erde soll bei -18°C in etwa 5.000 Metern „Abstrahlungshöhe“ mit 235 W/m² erfolgen. Die in Abbildung 2 „wolkig“ umrahmten (-0,65 °C pro 100m Höhengewinn) bezeichnen den vom EIKE-Admin ins Spiel gebrachten mittleren Temperaturgradienten aus der barometrischen Höhenformel, Zitat aus Wikipedia:
„Die barometrische Höhenformel beschreibt die vertikale Verteilung der (Gas-)Teilchen in der Atmosphäre der Erde, also die Abhängigkeit des Luftdruckes von der Höhe.“
Und weiter heißt es dort, Zitat:
„In Warmluftmassen und bei Aufgleitvorgängen nimmt der Temperaturgradient Werte um 0,3 bis 0,5 K pro 100 m an, in einbrechender Kaltluft meist um 0,6 bis 0,8 K pro 100 m, im Mittel über alle Wetterlagen 0,65 K pro 100 m.“
Eine Berechnung mit dem mittleren Gradienten der barometrischen Höhenformel ergibt nun 32,5°C für die durchschnittliche Temperaturdifferenz zwischen dem Erdboden (@NN) und der sogenannten Abstrahlungshöhe (@5.000m). Es ist schon mal höchst erstaunlich, dass sich aus der barometrischen Höhenformel ganz zwanglos dieselbe Temperaturdifferenz ergibt, die dem wissenschaftlich immer noch nicht nachgewiesenen „natürlichen atmosphärischen Treibhauseffekt“ in ebendiesen Grenzen zugeschrieben wird. Denn die barometrische Höhenformel basiert auf dem Verhalten der Atmosphäre im Schwerefeld der Erde und der sogenannte Treibhauseffekt soll auf dem Verhalten der Erde im Strahlungsfeld der Sonne beruhen. Sollte hier vielleicht bei den Treibhaus-Befürwortern eine phänomenale phänomenologische Verwechslung vorliegen?
Jedenfalls kann in diesem „Mittelerde“-Modell die ominöse THE-Temperaturdifferenz von 33°C durch Anwendung der barometrischen Höhenformel schon mal schlüssig erklärt werden. Diese Temperaturdifferenz impliziert dann wiederum eine Strahlungsdifferenz von 155 W/m² zwischen dem Erdboden (@NN) und der sogenannten Abstrahlungshöhe (@5.000m), die eindeutig der Umgebungsgleichung des Stefan-Boltzmann-Gesetzes folgt:
DELTA S = SIGMA (288K^4 – 255K^4) = 155 W/m²
Und eine solche Strahlungsdifferenz lässt sich dann sehr schön mit dem Poynting-Vektor beschreiben, Zitat Wikipedia (ex. Formeln):
„Der Poynting-Vektor S → {\displaystyle {\vec {S}}} (benannt nach dem britischen Physiker John Henry Poynting) kennzeichnet in der Elektrodynamik (einem Teilgebiet der Physik) die Dichte und die Richtung des Energietransportes (Energieflussdichte) eines elektromagnetischen Felds( E → , H → ) {\displaystyle ({\vec {E}},{\vec {H}})} . Der Begriff des Energieflusses ist identisch mit dem physikalischen Begriff der Leistung, die Bezeichnung Energieflussdichte ist daher gleichwertig zur Leistungsdichte.“
Abbildung 3 stellt die „Mittelerde“-Situation für die Abstrahlung zusammen mit dem Poynting-Vektor dar.
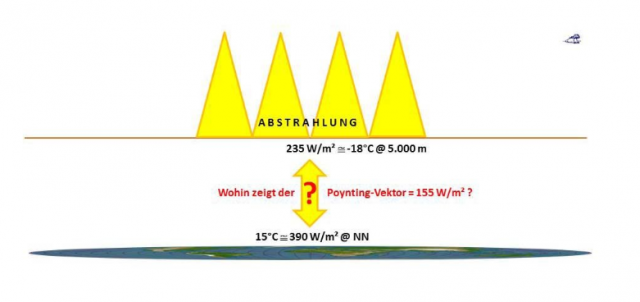
Abbildung 3: Abstrahlung im „Mittelerde“-Modell mit den zugehörigen Durchschnittstemperaturen und dem Poynting-Vektor Mit perspektivisch angepasster Mollweide-Projektion (Copyright L. Rohwedder – Lizenz CC BY-SA 3.0)
Die existenzielle Frage für den THE ist demnach, wohin dieser Poynting-Vektor zeigt. Dafür gibt es zunächst zwei Möglichkeiten:
- Der Poynting-Vektor zeigt von der „Abstrahlungshöhe“ nach „Mittelerde“ => Damit wäre der „natürliche atmosphärische Treibhauseffekt“ bewiesen.
- Der Poynting-Vektor zeigt von „Mittelerde“ zur „Abstrahlungshöhe“ => Damit wäre der „natürliche atmosphärische Treibhauseffekt“ widerlegt.
Nun ist Strahlung immer gerichtet, und der Poynting-Vektor definiert auch die Richtung dieser Strahlungsdifferenz zwischen „Mittelerde“ und „Abstrahlungshöhe“, Zitat Wikipedia (ex. Formeln):
„Mathematische Beschreibung: Der Poynting-Vektor ist ein dreikomponentiger Vektor, der in die Raumrichtung des Energieflusses zeigt. Er berechnet sich als das Kreuzprodukt aus elektrischer Feldstärke E → {\displaystyle {\vec {E}}} und magnetischer FeldstärkeH → {\displaystyle {\vec {H}}} .“
Da der Energiefluss eindeutig vom Warmen (@390W/m²) zum Kalten (@235W/m²) verläuft, ist auch die Richtung des Poynting-Vektors in Abbildung 3 eindeutig festgelegt, wie das nachfolgend in Abbildung 4 dargestellt wird.
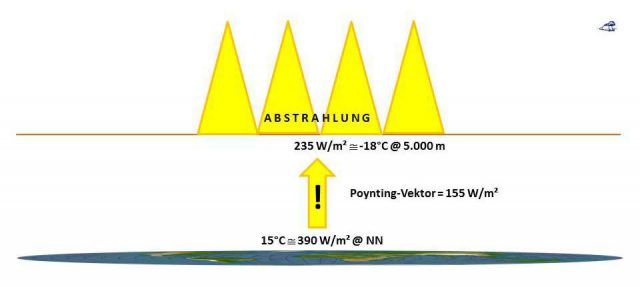
Abbildung 4: Die (Abstrahlungs-)Richtung des Poynting-Vektors im „Mittelerde“-Modell Mit perspektivisch angepasster Mollweide-Projektion (Copyright L. Rohwedder – Lizenz CC BY-SA 3.0)
Zum Beweis, dass der Energiefluss tatsächlich vom Warmen zum Kalten verläuft, wird nachfolgend der zweite Hauptsatz der Thermodynamik aus Wikipedia in der Formulierung von Clausius zitiert:
- „Es gibt keine Zustandsänderung, deren einziges Ergebnis die Übertragung von Wärme von einem Körper niederer auf einen Körper höherer Temperatur ist.“
Die Erklärung auf Wikipedia lautet, Zitat: „Wärme kann nicht von selbst von einem Körper niedriger Temperatur auf einen Körper höherer Temperatur übergehen. Diese Aussage scheint zunächst überflüssig zu sein, denn sie entspricht der alltäglichen Erfahrung. Dennoch ist sie gleichbedeutend zu allen weiteren, weniger „selbstverständlichen“ Aussagen, denn alle Widersprüche zu den anderen Aussagen lassen sich auf einen Widerspruch zu dieser zurückführen.“
Und damit gibt es in „Mittelerde“ auch keinen „natürlichen atmosphärischen Treibhauseffekt“.
Vielmehr wird das THE-Paradigma durch den Poynting-Vektor auf sein ursprüngliches „Arrhenius-Problem“ zurückgeworfen:
Die gemessenen Individualtemperaturen auf der Erde und deren vorgeblich gemittelter globaler Durchschnittswert können mit der fehlerhaften „Faktor4“-Anwendung des S-B-Gesetzes für die solare Einstrahlung nun mal nicht erklärt werden.
Und genau dieses Problem löst mein hemisphärischer S-B-Ansatz, indem dort die solare Einstrahlung auf die Tagseite beschränkt bleibt, ein diesbezügliches Zitat zur Erinnerung:
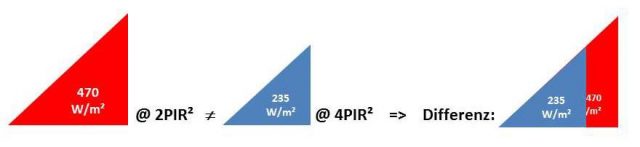
„Die nachfolgende vereinfachte Graphik möge also lediglich den Fehler einer globalen Mittelung verdeutlichen:
Der Strahlungsdurchschnitt von 470 W/m² (korrekt: 940W/m²* cosPHIi) umfass einen Strahlungsbereich von 0-940W/m² für die tagseitige Hemisphäre mit einem maximalen S-B-Temperaturäquivalent von 85,7°C @ 940W/m². Bei der globalen Mittelung der tagseitigen solaren Einstrahlung fällt also genau derjenige Teil der spezifischen solaren Strahlungsleistung weg, der Temperaturen oberhalb von (-18°C) erzeugen kann.“