[*Vorbemerkung der Redaktion: In Deutschland wird dieses Verfahren schon sehr lange nicht mehr angewendet. Hier wird die Tagesmitteltemperatur seit Jahr und Tag folgendermaßen ermittelt: T(7.00h) + T(14.00h) + 2 x T(21.00h)/4 (Angaben in MEZ). Als Grundlage dienten die sog. „Mannheimer Stunden“ (mehr dazu hier), definiert bereits im 18 Jahrhundert. Die Verdoppelung des Messwertes von 21 Uhr sollte einmal eine Nachtmessung ersparen, zweitens liegt er ziemlich genau zwischen den Tagesextremen und wird auch morgens durchlaufen.
In anderen europäischen Ländern, wie auch Russlands wurden andere Algorithmen verwendet. Allen ist gemeinsam, dass sie für denselben Tagestemperaturverlauf unterschiedliche Mitteltemperaturen ergeben. Details dazu z.B. hier. Fakt ist jedoch auch, dass bedingt durch die englische US- amerikanische Dominanz besonders im 19.Jahrhundert die Max Min Methode die weltweit bestimmende war.
Nach Erfindung der Digitalthermometer hat man die stündlichen Werte durch 24 dividiert, um die Tagesmittelwerte zu berechnen. Ein am Institut für Meteorologie viele Jahre lang durchgeführter Vergleich beider Verfahren zeigt zwar ähnliche Werte mit nur wenigen Ausnahmen aufgrund der Advektion unterschiedlich temperierter Luftmassen.
Da in jedem Fall die Anomalien der absoluten Mittelwerte gebildet werden, dürfte sich deren Verhalten, besonders in einer Zeitreihe, von der im Text beschriebenen unterscheiden. Für das Folgende spielen dieser Umstand auch nur eine untergeordnete Rolle. Man muss ihn aber bei der Lektüre im Hinterkopf behalten.
Trotzdem ist die Beachtung der in der Signaltheorie entwickelten Gesetze auch bei der Auswertung von meteorologischen Verläufen empfehlenswert. Autor Werner Kohl hat auf Die Kalte Sonne dazu schon einiges geschrieben. (hier)
Ende Einschub]
Allerdings ist die Lufttemperatur ein Signal, und Messungen von Signalen müssen den mathematischen Gesetzen der Aufbereitung von Signalen folgen. Das Nyquist-Shannon Sampling Theorem sagt uns, dass wir ein Signal mit einer Rate messen müssen, die mindestens doppelt so hoch ist wie die höchste Häufigkeits-Komponente des Signals. Das nennt man die Nyquist Rate. Sammelt man Proben mit einer geringeren Rate, kommt ein Alias-Fehler [? hier steht etwas dazu. Anm. d. Übers.] in die Messungen. Je geringer die Mess-Häufigkeit im Vergleich zu Nyquist, umso größer wird der Fehler bei Berechnungen der Mitteltemperatur und von Trends. Das Nyquist Sampling Theorem ist heutzutage grundlegende Wissenschaft in jedem technologischen Bereich. Digitales Hören und Sehen, industrielle Prozess-Steuerung, medizinische Instrumente, Flugkontroll-Systeme, digitale Kommunikation usw. – alles beruht auf der grundlegenden Mathematik und Physik von Nyquist.
Die NOAA hat in ihrem USCRN (US Climate Reference Network) bestimmt, dass es notwendig ist, eine Anzahl von 4320 Messungen pro Tag zu haben, um Nyquist anwenden zu können. 4320 Messungen pro Tag bedeuten eine Messung alle 20 Sekunden. Das ist die anwendungsorientierte Nyquist-Anzahl von Messungen. Die NOAA mittelt diese 20-Sekunden-Messwerte zu einer Messung alle 5 Minuten oder 288 Messungen pro Tag. Die NOAA veröffentlicht auch nur diese 288 Messungen pro Tag (nicht die 4320 Messungen pro Tag). Eine Rate wird dann nur aus diesen 288 Messungen pro Tag berechnet (oder „5-Minuten-Messungen). Diese Rate kann allerdings nur erhalten werden mittels automatisierten Messungen mit elektronischen Instrumenten. Die meisten instrumentellen Aufzeichnungen enthalten Ablesungen von Quecksilber-Max/Min-Thermometern, welche lange vor der Automatisierung eine Option waren. Heutzutage nutzt man für instrumentelle Aufzeichnungen trotz der Verfügbarkeit von Automatisierung immer noch Tmax und Tmin (im Endeffekt 2 Messungen pro Tag) anstatt einer Messdaten-Gewinnung nach Nyquist. Grund hierfür ist, die Vergleichbarkeit mit älteren historischen Aufzeichnungen zu wahren. Mit lediglich 2 Messungen pro Tag ist die instrumentelle Aufzeichnung jedoch stark aliased. In dieser Studie wird gezeigt, dass das historische Verfahren signifikante Fehler bei den Mitteltemperaturen und den langzeitlichen Temperaturtrends ergibt.
Das UACRN der NOAA ist ein kleines Netzwerk, welches im Jahre 2008 komplett war, und es trägt nur sehr wenig zu den instrumentellen Aufzeichnungen insgesamt bei. Allerdings bieten die USCRN-Daten eine besondere Gelegenheit, eine hochwertige Version des historischen Verfahrens mit dem Nyquist-Verfahren zu vergleichen. Die Max- und Min-Werte werden ermittelt mit den höchsten und niedrigsten Werten unter den 288 Messungen über den interessierenden 24-Stunden-Zeitraum.
Beispiele aus dem USCRN der NOAA zur Illustrierung des Effektes eines Verstoßes gegen das Nyquist-Theorem bzgl. der Mitteltemperatur
Das folgende Beispiel soll zeigen, wie der Fehler bei der Berechnung der Mitteltemperatur zunimmt, wenn die Anzahl der Messungen abnimmt. Abbildung 1 zeigt die Temperatur, wie sie am Messpunkt Cordova AK [= Alaska] am 11. November 2017 gemessen worden ist, und zwar mittels der 5-Minuten-Messungen nach USCRN:
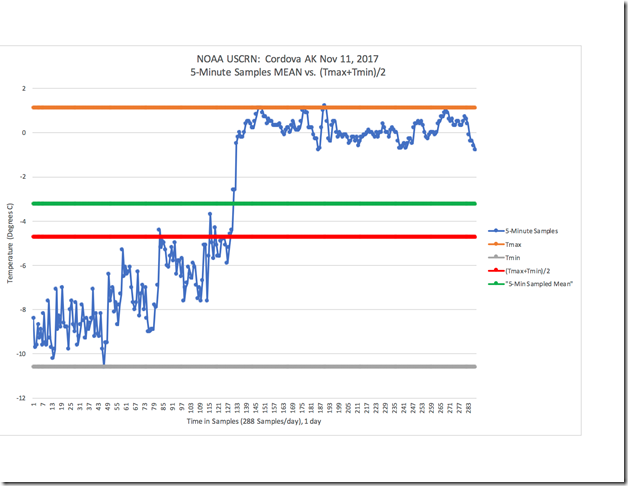
Abbildung 1: NOAA USCRN-Daten für Cordova, AK, am 11. November 2017
Die blaue Linie repräsentiert die 288 Temperaturmessungen jenes Tages. Sie zeigt 24 Stunden mit Temperaturdaten. Die grüne Linie zeigt die korrekte und genaue tägliche Mitteltemperatur, berechnet aus der Summe aller Messwerte dividiert durch die Anzahl der Messungen. Temperatur ist nicht Wärmeenergie, aber sie wird verwendet als eine Annäherung an dieselbe. In dieser Hinsicht zeigen die grüne Linie (Mitteltemperatur) und die Tageslinie (blaue Linie) genau die gleiche Menge von Wärmeenergie über den Zeitraum von 24 Stunden jenes Tages. Das korrekte Mittel beträgt -3,3°C. Tmax wird repräsentiert durch die orange, Tmin durch die graue Linie. Sie ergeben sich aus dem höchsten bzw. niedrigsten Wert der 288 Messungen über den 24-Stunden-Zeitraum. Das aus (Tmax + Tmin)/2 berechnete Mittel zeigt die rote Linie. (Tmax + Tmin)/2 ergibt einen Mittelwert von -4,7°C, weist also einen Fehler von 1,4°C im Vergleich zum korrekten Mittel auf.
[Dazu noch einmal zum Einschub oben: Bei dem zumindest in Deutschland gebräuchlichen Verfahren ist der Fehler geringer, was den Ausführungen des Autors zufolge aber auch daran liegen kann, dass es vier Messungen zu ganz bestimmten Zeiten sind und nicht nur zwei zu verschiedenen Zeiten am Tag. Daher zeigt sich in der folgenden Tabelle (Abbildung 2) bei 2 bzw. 4 Messwerten bei der Berechnung des Mittels der gleiche Fehler. Anm. d. Übers.]
Mit den gleichen Signalen und Daten aus Abbildung 1 zeigt die Tabelle in Abbildung 2 die berechneten Temperaturmittel in Abhängigkeit von einer immer weiter abnehmenden Zahl von Messwerten. Diese reduzierten Raten kann man mittels Division der 288 Messwerte pro Tag durch 4, 8, 12, 24, 48, 72 und 144 errechnen. Bei einer angemessenen Aussortierung der Messwerte nach diesem Verfahren ist der Gesamteffekt der gleiche, als ob man im Original mit reduzierter Rate gerechnet hätte. Das sich aus dieser reduzierten Anzahl von Messwerten ergebende korrespondierende Aliasing zeigt sich auch in der Tabelle:
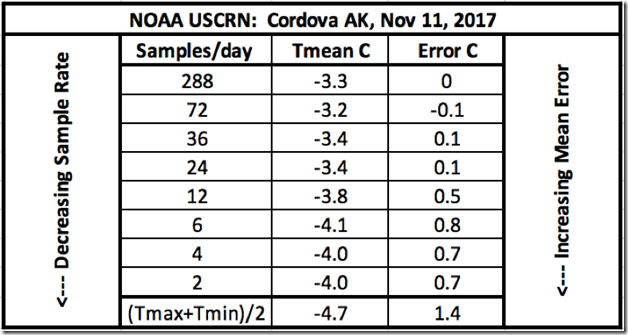
Abbildung 2: Tabelle mit den zunehmenden Mittelungsfehlern bei abnehmender Anzahl von Messwerten.
Aus der Tabelle geht klar hervor, dass bei Reduktion der Anzahl der Messwerte unter Nyquist der daraus erwachsende korrespondierende Fehler infolge des Aliasing zunimmt. Auch zeigt sich eindeutig, dass 2, 4, 6 oder 12 Messwerte pro Tag ein sehr ungenaues Ergebnis zeitigen. Eine Anzahl von 24 Messungen pro Tag (also stündlich) bis zu 72 Messwerten pro Tag (3 Messwerte innerhalb von 1 Stunde) kann genaue Ergebnisse erzielen – oder auch nicht. Die NOAA hat sich für 288 Messwerte pro Tag entschieden (4320 Messwerte pro Tag vor der Mittelbildung). Also wird das jetzt als der gegenwärtige Grund-Standard angesehen. Eine Anzahl von Messwerten unter 288 pro Tag wird (und sollte auch) als eine Verletzung des Nyquist-Theorems angesehen werden.
Es ist interessant darauf hinzuweisen, dass das in der Tabelle Gelistete einen Fehler von 0,7°C zeigt. Aber (Tmax + Tmin )/2 sind technisch 2 Werte pro Tag mit einem Fehler von 1,4°C, wie aus der Tabelle folgt. Wie kann das sein? Es kann sein, weil (Tmax + Tmin )/2 ein Sonderfall von 2 Messungen pro Tag ist, sind doch diese beiden Messungen nicht gleichmäßig über den Tag verteilt. Sie treten jeweils zu unterschiedlichen Zeiten auf. Bei geeigneten Messungen messen wir nach der Uhr – mit Messungen zu jeweils genau der gleichen Zeit an jedem Tag. Die Tatsache, dass Tmax und Tmin zu unregelmäßigen Zeiten am Tag auftreten, verursacht eine eigene Art von Messfehler. Es liegt jenseits dieser Studie, diesen in vollem Umfang zu erklären. Im Bereich der Signalanalyse und der Datengewinnung ist das ein bekanntes Problem. 2 Messungen pro Tag zu regelmäßigen Zeiten wird wahrscheinlich bessere Ergebnisse zeigen als das Auffinden der Höchst- und Tiefsttemperatur irgendeines gegebenen Tages. Die instrumentelle Temperaturaufzeichnung wendet das absolut schlechtestmögliche Verfahren an – was zu einem maximalen Fehler führt.
Abbildung 3 zeigt das gleiche tägliche Temperatursignal wie Abbildung 1, repräsentiert durch die 288 Messwerte pro Tag (blaue Linie). Ebenfalls gezeigt ist das gleiche tägliche Temperatursignal, errechnet aus 12 Messwerten pro Tag (rote Linie) und 4 Messwerten pro Tag (gelbe Linie). Aus dieser Abbildung geht schon für das bloße Auge hervor, dass viele Informationen des Original-Signals bei der Verwendung von nur 12 Werten pro Tag verloren gehen, und sogar noch mehr bei nur 4 Werten pro Tag. Es sind diese verloren gegangenen Informationen, welche das resultierende Mittel verfälschen. Diese Abbildung illustriert graphisch, was man in der korrespondierenden Tabelle von Abbildung 2 erkennt.
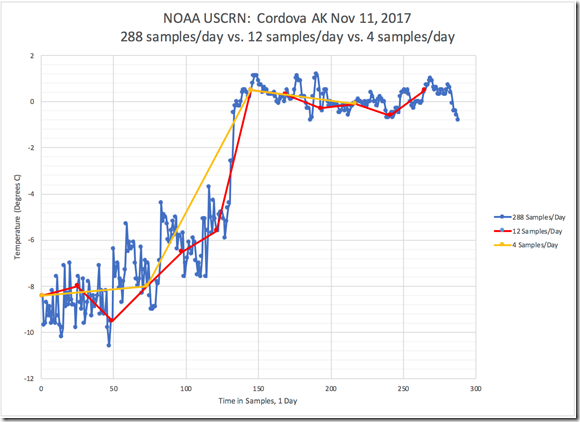
Abbildung 3: NOAA USCRN-Daten für Cordova, AK vom 11. November 2017: Abnehmende Detail-Genauigkeit des Mittelwertes bei 12 bzw. 4 Werten pro Tag.
Abbildung 4 zeigt den täglichen mittleren Fehler zwischen dem Verfahren mit 288 Werten pro Tag nach USCRN und dem historischen Verfahren, wie er über 365 Tage an der Station Boulder in Colorado im Jahre 2017 gemessen worden war. Jeder Datenpunkt ist der Fehler jedes einzelnen Tages in der Aufzeichnung. Man erkennt aus Abbildung 4, dass (Tmax + Tmin )/2 tägliche Fehler bis zu ± 4 °C erzeugt. Die Berechnung eines Mittelwertes mit nur zwei Werten pro Tag ergibt kaum jemals den korrekten Mittelwert.
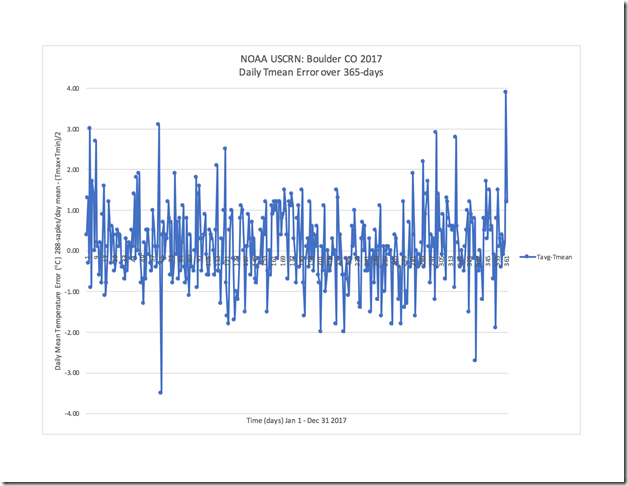
Abbildung 4: NOAA USCRN-Daten für Boulder, CO – täglicher Mittelungsfehler über 365 Tage (2017)
Betrachten wir noch ein weiteres Beispiel ähnlich dem in Abbildung 1 gezeigten, aber über einen längeren Zeitraum. Abbildung 5 zeigt (in blau) das 288 Werte pro Tag-Signal aus Spokane, WA [= Washington State, am Pazifik] vom 13. bis zum 22. Januar 2008. Tmax (mittel) und Tmin (mittel) sind jeweils in orange bzw. grau gezeigt. Das Mittel aus (Tmax + Tmin )/2 ist in rot dargestellt (-6,9°C) und das korrekte Mittel aus den alle 5 Minuten gemessenen Werten ist in grün dargestellt (-6,2°C). Das Mittel aus (Tmax + Tmin )/2 weist einen Fehler von 0,7°C über die 10-Tage-Periode auf.
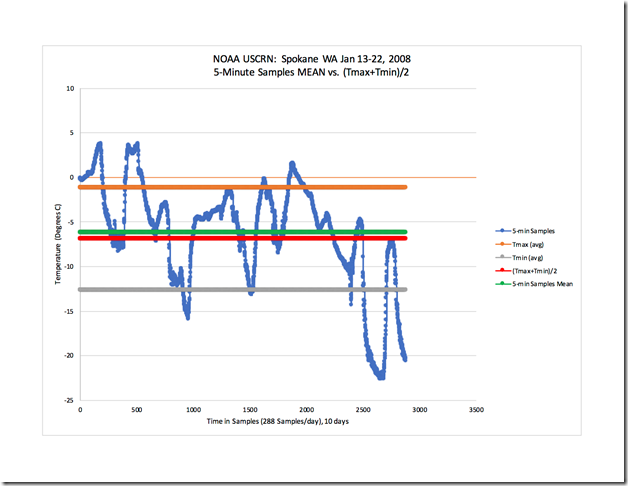
Abbildung 5: NOAA USCRN-Daten aus Spokane, WA – 13. bis 22. Januar 2008
Die Auswirkung einer Verletzung des Nyquist-Theorems auf Temperaturtrends
Schließlich müssen wir die Auswirkungen der Verletzung des Nyquist-Theorems bei der Anwendung auf Temperaturtrends betrachten. Abbildung 6 zeigt einen Vergleich zwischen linearen Temperaturtrends, wie sie sich aus dem historischen Verfahren ergeben, und Verfahren gemäß Nyquist unter Verwendung der Daten von Blackville, SC [= South Carolina], und zwar von Januar 2006 bis Dezember 2017. Man erkennt, dass der aus dem historischen Verfahren abgeleitete Trend (orange Linie) etwa 0,2°C wärmer anfängt und einen Erwärmungs-Bias von 0,24°C pro Dekade aufweist, jeweils im Vergleich zu dem Verfahren nach Nyquist (blaue Linie). Abbildung 7 zeigt den Trend-Bias oder Fehler (°C pro Dekade) für 26 Stationen im USCRN über einen Zeitraum von 7 bis 12 Jahren. Die 5-Minuten-Werte ergeben den Referenz-Trend. Fast jede Station zeigt einen Erwärmungs-Bias und nur wenige einen Abkühlungs-Bias. Der größte Erwärmungs-Bias beträgt 0,24°C pro Dekade und der größte Abkühlungs-Bias -0,17°C pro Dekade. Über alle 26 Stationen gemittelt ergibt sich ein Erwärmungs-Bias von 0,06°C. Wikipedia zufolge beträgt der berechnete globale Erwärmungstrend im Zeitraum 1880 bis 2012 0.064 ± 0.015°C pro Dekade. Schauen wir auf einen jüngeren Zeitraum, welcher den kontroversen „Stillstand der globalen Erwärmung“ enthält, und verwenden dann Daten von Wikipedia, erhält man die folgenden Erwärmungstrends – abhängig davon, welches Jahr man wählt als Beginn des „Stillstands“:
1996: 0.14°C pro Dekade
1997: 0.07°C pro Dekade
1998: 0.05°C pro Dekade
Obwohl man keine Schlussfolgerungen ziehen kann, wenn man die Trends über 7 bis 12 Jahre an 26 Stationen im USCRN vergleicht mit den gegenwärtig anerkannten lang- oder kurzzeitigen globalen Mitteltemperatur-Trends, kann dieser Vergleich instruktiv sein. Klar ist, dass die Anwendung des historischen Verfahrens zur Berechnung von Trends einen Trend-Fehler ergibt und dass dieser Fehler von ähnlicher Größenordnung sein kann wie die geltend gemachten Trends. Daher ist es vernünftig, die Validität der Trends zu hinterfragen. Es gibt keine Möglichkeit, diese Validität sicher herauszufinden, weil es bzgl. des Großteils der instrumentellen Aufzeichnung keine ordentlich errechnete Aufzeichnung zum Vergleich gibt. Aber mathematisch sicher ist, dass jede Mitteltemperatur und jeder Trend in den Aufzeichnungen signifikante Fehler enthält, falls das Verfahren der 2 Werte pro Tag angewendet worden ist.
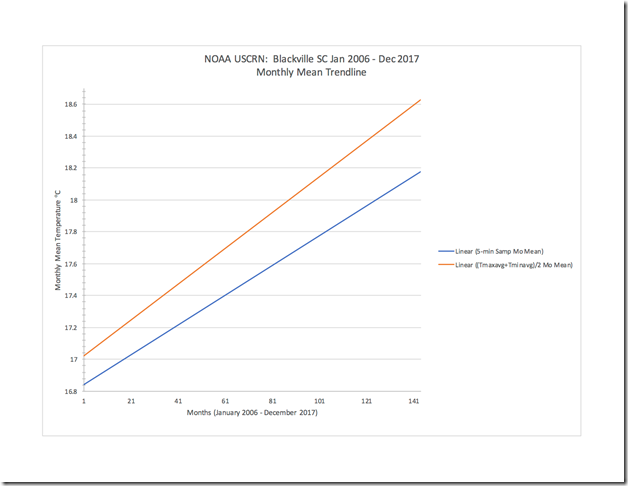
Abbildung 6: NOAA USCRN-Daten für Blackville, SC von Januar 2006 bis Dezember 2017 – monatliche Mittel-Trendlinien
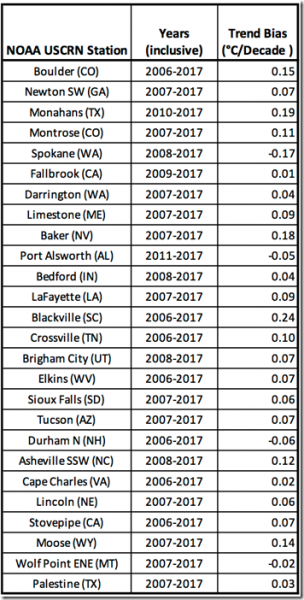
Abbildung 7: Trend-Bias (°C pro Dekade) für 26 Stationen im USCRN
Schlussfolgerungen
1. Die Lufttemperatur ist ein Signal und muss daher gemessen werden nach den mathematischen Gesetzen, welche die Signalverarbeitung bestimmen. Die Wertesammlung muss gemäß dem Nyquist Shannon-Sampling Theorem durchgeführt werden.
2. Das Nyquist Shannon-Sampling Theorem ist seit über 80 Jahren bekannt und von grundlegender Bedeutung in jedem Technologiebereich, bei dem es um Signalverarbeitung geht. Eine Verletzung von Nyquist garantiert, dass die Werte korrumpiert sind mit einem Aliasing-Fehler, und die Werte werden nicht das sich ergebende Signal repräsentieren. Aliasing kann nach der Werte-Gewinnung nicht korrigiert werden.
3. Das Nyquist Shannon-Sampling Theorem erfordert, dass die Rate der Anzahl der Werte größer sein muss als 2 mal die höchste Häufigkeits-Komponente des Signals. Unter Verwendung automatisierter elektronischer Ausrüstung und Computer erstellt das NOAA USCRN Wertemengen mit einer Rate von 4320 Werten pro Tag (gemittelt zu 288 Werten pro Tag), um Nyquist praktikabel anwenden zu können und einen Aliasing-Fehler zu vermeiden.
4. Die instrumentelle Temperaturaufzeichnung beruht auf dem historischen Verfahren der Berechnung aus den Werten der täglichen Höchst- und Tiefsttemperatur. Daher verletzt die instrumentelle Aufzeichnung das Nyquist Shannon-Sampling Theorem.
5. Das USCRN der NOAA ist ein hochwertiges Datengewinnungs-Netzwerk, welches in der Lage ist, ein Temperatursignal ordentlich zu messen. Das USCRN ist ein kleines, im Jahre 2008 vervollständigtes Netzwerk und trägt nur wenig zu der gesamten instrumentellen Aufzeichnung bei. Allerdings bieten die USCRN-Daten eine besondere Gelegenheit, Analyse-Verfahren miteinander zu vergleichen. Ein Vergleich kann erfolgen zwischen Temperatur-Mittelwerten und Trends, errechnet aus Tmax und Tmin und einem ordentlich ermittelten Signal gemäß Nyquist.
6.Mittels der Verwendung einer begrenzten Anzahl von Beispielen aus dem USCRN wurde gezeigt, dass die Verwendung von Tmax und Tmin als Datenquelle die folgenden Fehler ergeben kann im Vergleich zu einem gemäß Nyquist ermittelten Signal:
a) Einen mittleren Fehler, der von Station zu Station sowie von Tag zu Tag an einer Station variieren kann.
b) einen mittleren Fehler, der mit der Zeit variiert mit einem mathematischen Anzeichen, welches sich ändern kann (positiv/negativ)
c) Tägliche mittlere Fehler bis zu ±4°C
d) Langzeitliche Trendfehler mit einem Erwärmungs-Bias bis zu 0,24°C pro Dekade und einem Abkühlungs-Bias bis zu -0,17°C pro Dekade.
7. Die volle instrumentelle Aufzeichnung weist keine angemessen ermittelte Wertemenge auf für einen Vergleich. Es bedarf weiterer Arbeiten, um zu bestimmen, ob eine theoretische Obergrenze berechnet werden kann für den Mittelungs- und den Trendfehler, der sich ergibt bei der Anwendung des historischen Verfahrens.
8. Das Ausmaß des beobachteten Fehlers mit der damit verbundenen Größenordnung der Unsicherheit stellen den wissenschaftlichen Wert der instrumentellen Aufzeichnung in Frage sowie auch die Praxis, Mittelwerte und langzeitliche Trends aus Tmax und Tmin zu berechnen.
Referenzen:
This USCRN data can be found at the following site: https://www.ncdc.noaa.gov/crn/qcdatasets.html
NOAA USCRN data for Figure 1 is obtained here:
https://www1.ncdc.noaa.gov/pub/data/uscrn/products/subhourly01/2017/CRNS0101-05-2017-AK_Cordova_14_ESE.txt
NOAA USCRN data for Figure 4 is obtained here:
https://www1.ncdc.noaa.gov/pub/data/uscrn/products/daily01/2017/CRND0103-2017-AK_Cordova_14_ESE.txt
NOAA USCRN data for Figure 5 is obtained here:
https://www1.ncdc.noaa.gov/pub/data/uscrn/products/subhourly01/2008/CRNS0101-05-2008-WA_Spokane_17_SSW.txt
NOAA USCRN data for Figure 6 is obtained here:
https://www1.ncdc.noaa.gov/pub/data/uscrn/products/monthly01/CRNM0102-SC_Blackville_3_W.txt
————————–
Die gesamte 21 Seiten starke Studie kann hier heruntergeladen werden (PDF).
Link: https://wattsupwiththat.com/2019/01/14/a-condensed-version-of-a-paper-entitled-violating-nyquist-another-source-of-significant-error-in-the-instrumental-temperature-record/
Übersetzt von Chris Frey EIKE







