Eine Analyse der Thesen/Antithesen für einen „natürlichen atmosphärischen Treibhauseffekt“ – Teil 1: Gegenüberstellung der Thesen/Antithesen
Für einen solchen „natürlichen atmosphärischen Treibhauseffekt“ gibt es unterschiedliche Modelle, einen experimentellen Ansatz und zwei Widerlegungen. Nachfolgend werden die wesentlichen THE-Thesen/Antithesen vorgestellt; Nischentheorien werden hier nicht berücksichtigt.
THESE (1): Der konventionelle globale Stefan-Boltzmann-Ansatz mit einem „natürlichen atmosphärischen Treibhauseffekt“ von 33°C, der als Differenz zwischen einer vorgeblich „natürlichen“ theoretischen Temperatur unserer Erde von -18°C aus der der globalen Strahlungsbilanz und einer vorgeblich „gemessenen Globaltemperatur“ NST von 14,8°C abgeleitet wird.
These(1.1): Die Erde wird als ein selbstleuchtender Stern betrachtet. Dazu wird der temperaturwirksame Anteil der Solarstrahlung über die gesamte Erdoberfläche gemittelt und mittels Stefan-Boltzmann-Gesetz eine Art „Abstrahlungstemperatur“ für die Erde umgerechnet. Der „natürliche atmosphärische Treibhauseffekt“ erklärt sich dann als Differenz zur vorgeblich „gemessenen Globaltemperatur“ NST.
Vertreter: IPCC-TAR-Gutachter Dipl.-Ing Peter Dietze
Referenz zu (1.1): Kommentar P. Dietze vom 5. August 2019 um 9:54 auf EIKE
Kernaussage (1.1), Zitat aus der Referenz mit Hervorhebungen: „Herr Schulz, der Geometriefaktor der (rotierenden, gut speichernden und Wärme umverteilenden) Erdkugel ist 4. Wie auch Herr Weber angibt, erhält die Erde 4PiR²*235 W/m2 an mittlerer Einstrahlung. Da 1 W ein Joule/s ist, können Sie Ihre Zahl mit dem Erdradius leicht selbst ausrechnen. Wenn man 235 W/m² in Stefan-Boltzmann einsetzt, ergeben sich knapp 255 K. Die mittlere Bodentemperatur ist aber um 33 K höher – und das ist der Treibhauseffekt, den Herr Weber hinweg zu schummeln versucht.“
Herr Dietze hatte seine Berechnungen in einer E-Mail vom 06.09.2019 um 11:01pm an Dr. Kramm auf dem üblichen Skeptiker-Verteiler noch weiter spezifiziert, Zitat mit Hervorhebungen:
„Die S-B-Gleichung für den Treibhauseffekt lautet für das quasi isotherme Strahlungsmodell der rotierenden Erde mit 30% Wolkenalbedo und ansonsten solar transparenter Atmosphäre im Strahlungsfliessgleichgewicht mit
S=absorbierter Solarstrahlung, im Mittel 240 W/m²
T=solar bedingter Bodentemperatur, im Mittel 255K
G=Gegenstrahlung 150 W/m²
==> S+G = Sigma*(T+deltaT)^4
Daraus ergibt sich deltaT=33 K und somit die Bodentemperatur zu T=288 K (+15 Grad) wie beobachtet. Q.e.d.“
These (1.2): Die Klimawirksamkeit von Treibhausgasen
These (1.2.1): Der „natürliche atmosphärische Treibhauseffekt“ beim konventionellen S-B-Ansatz wird durch Treibhausgase erzeugt.
Vertreter: Der Geophysiker Michael Krüger (ScienceScepticalBlog)
Referenz zu (1.2.1): „Grundlagen des Treibhauseffektes für EIKIANER“ (2016)
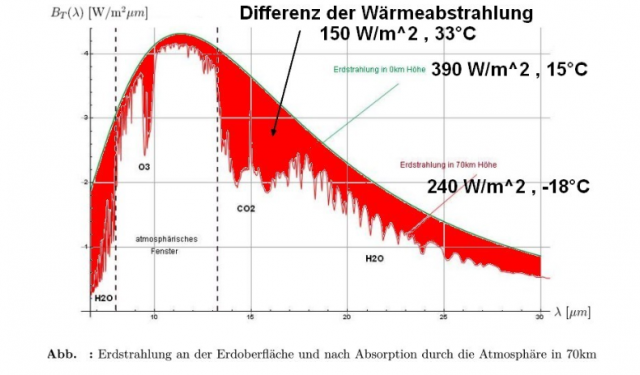
Kernaussage (1.2.1), Zitat aus der Referenz mit Hervorhebungen: „Die Erdoberfläche strahlt Wärme mit durchschnittlich 390 Watt pro Quadratmeter ab. Das entspricht der Wärmeabstrahlung eines sog. Schwarzen Körpers bei 15°C. In 70 km Höhe strahlt die Erde nach Absorption durch Treibhausgase und Wolken innerhalb der Atmosphäre nur noch Wärme mit durchschnittlich 240 Watt pro Quadratmeter ab. Das entspricht der Wärmeabstrahlung eines sog. Schwarzen Körpers bei -18°C. Die Differenz zwischen Boden und 70 km beträgt 150 Watt pro Quadratmeter und 33°C. Das ist die sog. Differenz für den natürlichen Treibhauseffekt.“
Und weiter unten heißt es dort, Zitat mit Hervorhebungen: „Sog. Treibhausgase wie CO2 und Wasserdampf und auch Wolken führen durch ihre Absorptions- und Strahlungseigenschaften von Wärmestrahlung dazu, dass wir eine Differenz von ca. 33°C zwischen Erdoberfläche und 70 km Höhe messen.“
These (1.2.2): Der „natürlichen atmosphärische Treibhauseffekt“ durch Treibhausgase konnte experimentell nachgewiesen werden.
Vertreter: Herr Dr. Michael Schnell (EIKE)
Referenz zu (1.2.2): „Experimentelle Verifikation des Treibhauseffektes – 4. Mitteilung: die erdnahe CO2-Strahlung“ (2019)
Kernaussage (1.2.2-1), Zitat aus der Referenz mit Hervorhebungen:
„Anfang des 19. Jahrhunderts suchten verschiedene Forschergruppen einen mathematischen Zusammenhang zwischen Temperatur und IR-Strahlung eines Körpers. Unter anderen Dulong und Petit, die die Abkühlung eines heißen Thermometers (200 – 300 °C) in einem kalten Vakuumgefäß verfolgten (Abb. 3) [9]. Sie entwickelten eine einfache Formel, die hinreichend genau die zeitliche Abkühlung des Thermometers wiedergab. Die Gleichung versagte jedoch, wenn wesentlich heißere Körper, wie die der Sonne, berechnet werden sollten.
Josef Stefan überprüfte die Versuche von Dulong und Petit und anderer Forschergruppen und konnte rein empirisch Gl. 1 ermitteln, womit die Wärmeübertragung P paralleler Oberflächen, auch bei sehr hohen Temperaturen, berechnet werden konnte [8]. Stefan brauchte den sogenannten Strahlungsaustauschgrad „E“ für blanke, also reflektierende Oberflächen (Emissionsgrad ε << 1). Geht man aber von einer Schwarz-Körper-Strahlung mit ε = 1 aus, wird auch E = 1 und wir haben mit Gleichung Gl. 2 den Vorläufer des Stefan-Boltzmann-Gesetzes (Gl. 3) vor uns, das von Ludwig Boltzmann 1884, einem Schüler von Stefan, theoretisch abgeleitet wurde [10].
Mit Gl. 2 legt Stefan die Grundlage für die Berechnung des Treibhauseffektes. Die Abkühlung des Thermometers (Energieverlust) hängt sowohl von der Temperatur T1 als auch von T2 ab, also von der Differenz zwischen Ausstrahlung des Thermometers und Gegenstrahlung der Kupferwand.“
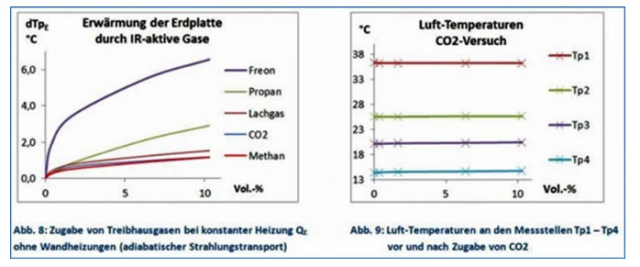
Kernaussage (1.2.2-2), Zitat aus der Referenz mit Hervorhebungen: „… In einem bereits publizierten Demonstrations-Experiment [12], [11] wurden unter adiabatischen Bedingungen (ohne Wandheizung) die Auswirkungen von CO2 (und anderen Treibhausgasen) untersucht. Dabei wurde eine deutliche Erwärmung der Erd-Platte beobachtet, während innerhalb der Röhre, an den Messstellen Tp1 – Tp4, die Temperaturen konstant blieben (Abb. 8 und 9)…“
These (1.3): Gegenüber einer variablen „gemessenen Globaltemperatur“ verändert sich die „Abstrahlungstemperatur“ der Erde nicht. Vielmehr beträgt die Abstrahlungsleistung der Erde beim konventionellen S-B-Ansatz immer 239 W/m². Bei einer Veränderung der Globaltemperatur NST verändert sich lediglich die „Abstrahlungshöhe“ bei -18°C.
Vertreter: Der Astrophysiker Dr. Peter Heller (ScienceScepticalBlog)
Referenz: „Der Treibhauseffekt“ (2010)
Kernaussage (1.3), Zitat aus der Referenz mit Hervorhebungen: „Der Ansatz der Klimaforschung wird nun deutlich: Wenn man die Menge an Treibhausgasen in der Troposphäre steigert, erhöht sich die „Grenzschicht“, ab der die Atmosphäre für IR-Strahlung durchsichtig wird. Die Temperatur dieser „Grenzschicht“ ist aber immer -18° (aufgrund des oben angenommenen Strahlungsgleichgewichtes). Liegt sie nur 100 Meter höher, steigt dadurch die Temperatur der Luft am Erdboden um im Mittel 0,65° (es liegen dann eben nicht mehr 5 km Luft zwischen dieser Schicht und dem Erdboden, sondern 5,1 km).“
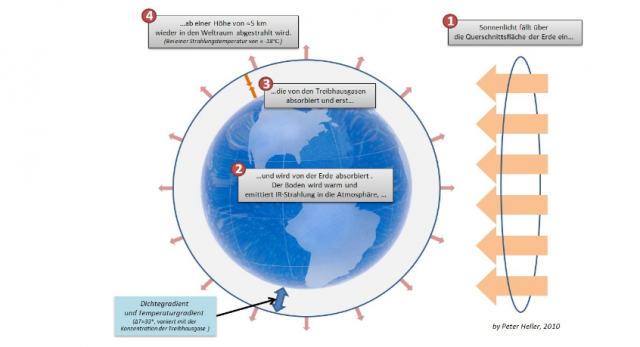
Abbildung: Abstrahlungshöhe aus „Der Treibhauseffekt“ von Dr. Peter Heller (2010 @ ScienceScepticalBlog)
THESE (2): Ein globales Modell analog zum konventionellen S-B-Ansatz mit einem global breitenabhängig gemittelten Strahlungsansatz und einem begrenzten thermischen „Slab“-Zwischenspeicher.
Vertreter: Kramm et al. (2017)
Referenz (2): “Using Earth’s Moon as a Testbed for Quantifying the Effect of the Terrestrial Atmosphere”
Kernaussage (2.1): Zitat aus Kramm et al. (2017) mit Hervorhebungen: “The results of our numerical simulations using the multilayer-force-restore method for the 27.4 times higher angular velocity of the Earth are illustrated in Figure 22. Part (a) of this figure shows the daily mean slab temperature as a function of latitude and terrestrial day of the year.” (S. 281 3. Absatz)
Dazu der unabhängige Google-Übersetzer (mit Korrektur): „Die Ergebnisse unserer numerischen Simulationen unter Verwendung der Multilayer-Force-Restore-Methode für die 27,4-fach höhere Winkelgeschwindigkeit der Erde sind in Abbildung 22 dargestellt. Teil (a) dieser Abbildung zeigt die tägliche mittlere Plattentemperatur als Funktion von Breite und Breite Erdtag des Jahres.“
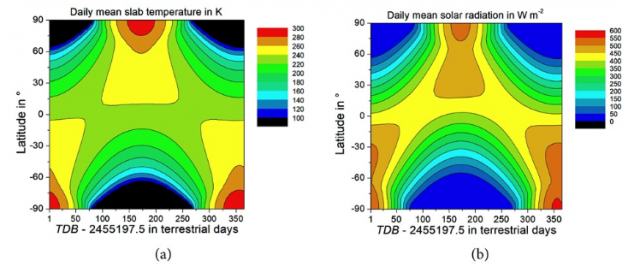
Abbildungen 22 a und b aus Kramm et al. (2017) (Creative Commons License CC BY 4.0)
Kernaussage (2.2): Zitat Kramm et al. (2017) mit Hervorhebungen: “Thus, one has to conclude that concept of the effective radiation temperature oversimplifies the physical processes as it ignores the impact of local temperatures on the fluxes in the planetary radiative balance.” (S. 283 letzter Absatz, letzter Satz)
Dazu der unabhängige Google-Übersetzer: „Daher muss man schließen, dass das Konzept der effektiven Strahlungstemperatur die physikalischen Prozesse zu stark vereinfacht, da der Einfluss lokaler Temperaturen auf die Flüsse im Strahlungshaushalt des Planeten ignoriert wird.“
THESE (3): Eine „globale“ Stefan-Boltzmann-Integration, die in einem Widerspruch mit dem Betrag des „natürlichen atmosphärischen Treibhauseffektes“ von 33°C aus Modell (1) endet.
Vertreter: Prof. Dr. Gerlich (†) und Dr. Ralf D. Tscheuschner, Hamburg
Referenz (3) „Falsifizierung der atmosphärischen CO2 -Treibhauseffekte im Rahmen der Physik“
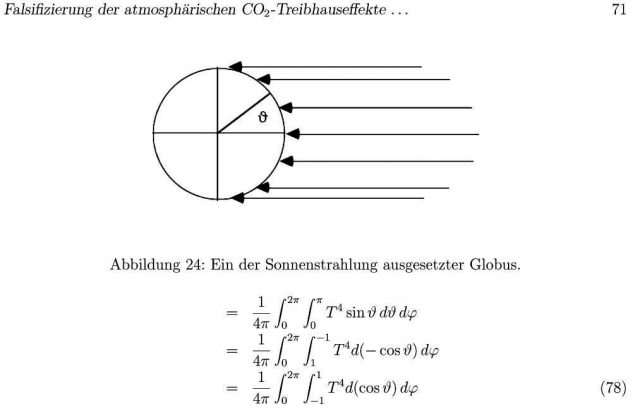
Kernaussage: Gerlich and Tscheuschner (2009) leiten eine Stefan-Boltzmann-Integrallösung für die Durchschnittstemperatur der gesamten Erdoberfläche (4PIR2) her:
Diese berechnete physikalische Globaltemperatur Tphys beträgt -129 °C, respektive 144,15 K für die gesamte Erdoberfläche (4PIR2) und würde daher zur Erklärung der vorgeblich „gemessenen“ globalen Durchschnittstemperatur einen Treibhauseffekt von weiteren 144 °C erfordern. Aus dem Widerspruch (33°C # 144°C) leiten Gerlich und Tscheuschner ab, dass es keinen „natürlichen atmosphärischen Treibhauseffekt“ gibt.
THESE (4): Ein „hemisphärischer“ Stefan-Boltzmann-Ansatz ohne einen atmosphärischen Treibhauseffekt, bei dem die (hemisphärische) Temperaturgenese nach dem S-B-Gesetz auf die Tagseite der Erde beschränkt bleibt, während die Abstrahlung der gesamten Erdoberfläche über dessen Umgebungsgleichung erfolgt.
Vertreter: Uli Weber (DGG und EIKE)
Referenz (4) „Weitere Überlegungen zur hemisphärischen Herleitung einer globalen Durchschnittstemperatur“ @ DGG-Mitteilungen 1/2019:18-25
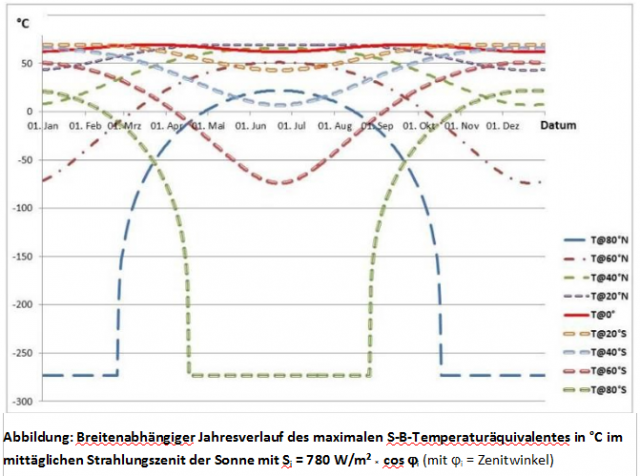
Anmerkung: Hier wird ein Zweischichtfall für Erde-Atmosphäre mit Seff = 780 W/m² dargestellt, während ich in meinen Blogartikeln einen Einschichtfall mit Seff = 940 W/m² betrachte.
Kernaussage (4): Die Temperaturgenese erfolgt ausschließlich auf der sonnenbeschienenen Tagseite unserer Erde. Zwischen den Wendekreisen und bis in die mittleren Breiten der Sommerhemisphäre werden gleichzeitig die „Energiespeicher“ unserer Erde (Atmosphäre und Ozeane) durch die Sonneneinstrahlung aufgeladen und damit das maximale S-B-Temperaturäquivalent nicht erreicht. Die Nachtseite im Tagesverlauf und die höheren Breiten im Jahresverlauf, insbesondere auf der Winterhemisphäre, profitieren durch Wärmeadvektion von den dort erwärmten globalen Zirkulationen über die S-B-Umgebungsgleichung.
Um es noch einmal ganz deutlich zu machen: Nur in Ausnahmefällen (hocharide Wüstengebiete in niederen Breiten) wird das rechnerische S-B-Temperaturäquivalent (SBT) auf der Tagseite der Erde erreicht. Die Energiedifferenz zwischen dem SBT und der tatsächlichen Ortstemperatur in [W*s=J] fließt üblicherweise in die globalen Zirkulationen (Atmosphäre und Ozeane) – respektive wird die Ortstemperatur nachts und im Winterhalbjahr daraus unterstützt.
In Teil 2 werden die hier vorgestellten Thesen/Antithesen dann ausführlich diskutiert.