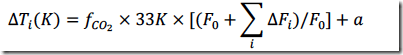Die schmutzigen Tricks der Windindustrie

geschrieben von H.j. Lüdecke | 22. Oktober 2019

Der Windradausbau stockt, weil die Bürger sich diesen schädlich teuren Unsinn nicht mehr gefallen lassen und zunehmend den Kadi einschalten. Wenn das einmal nichts mehr nützen sollte, könnte man mit mehr rechnen, denn auch die Geduld des lammfromm-untertänigen Deutschen hat einmal seine Grenzen. Die französischen Gelbwesten und nun die holländischen Bauern sind ein Vorgeschmack. Warum ist eigentlich der Druck so groß? Die Antwort auf dieses Rätsel ist leider nicht ausreichend bekannt: In Gesamtspektrum des deutschen Klima-, CO₂-, Energiewende-, Gender- und weiterer geldverschlingender Zirkusse haben sich inzwischen viele Hunderttausende Profiteure parasitär eingenistet. Die leben davon, saugen an den Zitzen einer (noch) steuerfetten Staats-Sau, die auf der anderen Seite den wirklich produktiv Arbeitenden dieses Landes das letzte Haar vom Kopf wegfrisst.

Produktives erschaffen diese Parasiten nicht. Die Krankheit ist zu erkennen an der desolaten Infrastruktur von zerfallenden Brücken, Schulen, Bahn sowie einer dysfunktionalen Bundeswehr, um nur einige stellvertretende Baustellen zu nennen. Sie ist nur mit dem Heilmittel einer schweren Rezession zu beseitigen, weil dann kein Geld mehr für Unsinn da ist. Dann wird aber leider auch der Staatsköper selber geschädigt – die Kur entspricht also leider dem früheren Quecksilber gegen Syphilis.

Nur ein harmloses stellvertretendes Beispiel: Inzwischen haben sich auch an den Hochschulen Bewegungen etabliert, die sich Scientists for Future (SFF) nennen. Zu attraktiv sind die Fördertöpfe für Forschungs- und Lehrvorhaben und zu verwirrt die Köpfe. Falls SFF nur über Facebook läuft, ist dagegen nichts einzuwenden. Auch Professoren ist es erlaubt, geistigen Schwachsinn offen zu demonstrieren. Wenn dieser SFF-Unsinn aber von Hochschulleitungen selbst propagiert wird, ist es bedenklich.

Nun zu den Windindustrieprofiteuren: Kürzlich veranstaltete die Bundesregierung einen „Windgipfel“, s. hierzu die Veröffentlichung von Holger Douglas, in Tichys Einblick (TE) vom 7.Sept.2019 (hier), Dazu eingeladen waren allerdings nur die windindustriefreundlichen „NGOs“, s. wieder H. Douglas in TE, 23.August2019 (hier). Sie forderten u.a. eine Aufweichung des Artenschutzes, um ihre Ausbaupläne noch ungehemmter vorantreiben zu können; dagegen regt sich Widerstand in Form einer öffentlichen Petition (hier).

Die Windindustrie-Lobby versucht zu suggerieren, das Umwelt- und Planungsrecht sei zu restriktiv bei der Zulassung von Windindustrieanlagen. Das genaue Gegenteil trifft zu; schon heute genießt die Windindustrie eine Reihe sachlich nicht gerechtfertigter Privilegierungen im Umwelt und Planungsrecht gegenüber sonstigen Industrieanlagen (inzwischen 240 m hohe Windräder sind Industrieanlagen!). Die Privilegierungen werden benannt in Ziff. 4 einer Forderungsliste Odenwälder Bürgerinitiativen 10 Punkte_Odenwald. Diese von der Windindustrie-Lobby schon früher durchgesetzten Privilegierungen sind sehr geschickt z.B. versteckt in Anhängen zum UVPG (= Gesetz über die Umweltverträglichkeitsprüfung oder UVP-Gesetz) und zur der 4. BImSchV [1].

Dank der dort genannten Schwellenwerte braucht der Projektierer ein größeres Ausbauprojekt einfach nur in Einzelprojekte unterhalb des Schwellenwerts aufspalten, und schon erspart er sich eine volle UVP oder ein volles BImSchG-Genehmigungsverfahren mit Öffentlichkeitsbeteiligung. Eine weitere Privilegierung findet sich im Bauplanungsrecht in § 35 BauGB (= Baugesetzbuch). Sie hat zur Folge, dass einem Windindustrieprojekt entgegenstehende private, nicht privilegierte Belange kaum noch entgegengehalten und entgegenstehende öffentliche Belange wie Natur- und Landschaftsschutz leichter überwunden werden können. Für eine im privaten Renditeinteresse errichtete Anlage ist diese Besserstellung gegenüber anderen Industrieanlagen völlig sachwidrig und nicht zu rechtfertigen. Die BI fordern deshalb zu Recht die ersatzlose Streichung dieser Privilegierungen im Umwelt- und Planungsrecht. Keinesfalls dürfen gar noch weitere Privilegierungen hinzukommen, wie auf dem Windgipfel gefordert.

Pikanterweise hat auch schon der NaBu in der Vergangenheit diese Privilegierungen kritisiert (NABU-Positionspapier „Windenergie – Naturverträgliche Nutzung der Windenergie an Land und auf See“ von November 2016, S. 3 Mitte; S. 6 unter 12; S. 13 unter 3) 170320_NaBU_positionspapier_naturverträgliche_nutzung_der_ windenergie. Allerdings hat dieses Positionspapier ein eingebautes „Verfallsdatum“, und eine Bestätigung erscheint fraglich; auch der NaBu wird zunehmend, wie seit jeher der BUND, von der Windindustrie-Lobby unterwandert. Nur die von Enoch zu Guttenberg gegründete Naturschutzinitiative (Vors. Harry Neumann) ist noch windindustriekritisch.

Dies ist umso unverständlicher, da gerade für diejenigen, die der These von der menschengemachten Klimaerwärmung anhängen, ein Windindustrie-Ausbau im Wald ein Tabu sein müsste (hier): Im Gegenteil müsste man dann eigentlich für einen noch viel konsequenteren Schutz Waldschutz als bisher eintreten (hier).

Quellen

[1] BImSchV „Verordnung zur Durchführung des BImSchG“; es gibt davon mehrere; die 4. Durchführungsverordnung legt fest, welche Anlagen genehmigungsbedürftig sind und in welchem Verfahren (vereinfachtes ohne Öffentlichkeitsbeteiligung oder volles Genehmigungsverfahren mit Öffentlichkeitsbeteiligung), aufgelistet in Anlage 1 zur 4. BImSchV

Warum die Kritik von Roy Spencer unzutreffend ist

geschrieben von Chris Frey | 22. Oktober 2019

Vier Tage später veröffentlichte Roy Spencer Kritik an meiner Analyse bei WUWT, und zwar hier ebenso wie auf seinem eigenen Blog hier. Am nächsten Tag folgte bei WUWT hier ein Folgebeitrag dazu. Auf seinem Blog finden sich auch zwei weitere Kritiken, nämlich hier und hier.

Komischerweise postete Roy drei Tage vor seiner Kritik an meiner Arbeit einen Beitrag mit dem Titel [übersetzt] „Die Komponente des Glaubens bei Globale-Erwärmung-Prophezeiungen“ (hier). Er kam zu dem Ergebnis, dass Klima-Modellierer lediglich gezeigt hätten, was sie von Anfang an vermutet hatten. Sie machen sich eines Zirkelschlusses schuldig und haben eine Doppelaussage abgegeben.

Roy folgerte: „Ich sage nicht, dass ein zunehmender CO₂-Gehalt keine Erwärmung verursacht. Ich sage, dass wir keine Ahnung haben, wie viel Erwärmung es verursacht, weil wir keine Ahnung haben, wie groß das natürliche Energie-Ungleichgewicht im Klimasystem ist während der letzten – sagen wir – 50 Jahre. … Folglich weisen Projektionen der globalen Erwärmung einen großen Anteil von Glauben auf, der in die Modelle einprogrammiert wurde“.

Roys Schlussfolgerung entspricht ziemlich genau derjenigen in meiner Studie, welche der danach kritisierte.

In diesem Beitrag werde ich die Kritikpunkte von Roy an meiner Arbeit aufgreifen und zeigen, warum jeder einzelne dieser Kritikpunkte falsch ist.

Welche Punkte kritisiert er nun? Er sagt:

1) Meine Fehlerfortpflanzung prognostiziert sehr große Abweichungen der Temperatur.

2) Klimamodelle weisen KEINE substantiellen Fehler in ihrem Gesamt-Energiefluss an der Obergrenze der Atmosphäre [TOA] auf.

3) Das Modell der Fehlerfortpflanzung ist für Klimamodelle nicht geeignet!

Darum soll es im Folgenden gehen. Es wird ein langer Beitrag. Falls man es in einem Satz zusammengefasst haben will: alle Kritikpunkte von Roy zeigen, dass er etwas erheblich falsch verstanden hat.

1) Meine Fehlerfortpflanzung prognostiziert sehr große Abweichungen der Temperatur.

Roy schrieb: „Frank zieht in seiner Studie als Beispiel einen bekannten Bias heran beim langwelligen (infrarot) Wolken-Antrieb (LWCF) in einem typischen Klimamodell und vermutet, dass der typische Fehler des Modells (±4 W/m²) im LWCF auf seine nachgebildete Modellgleichung angewendet werden kann, was den Fehler zeitlich in die Zukunft fortsetzt während der Integration in seinem nachgebildeten Modell. Die Folge ist eine gewaltige falsche Modell-Erwärmung (oder -Abkühlung) bis zu 20°C oder mehr bei der zukünftigen mittleren Lufttemperatur (GASAT). (Hervorhebung von mir [= dem Autor])

Für jedermanns Aufmerksamkeit – Roy fährt fort: „Die Modellierer sind sich dieser Verzerrungen (im Wolkenanteil) sehr bewusst, welche positiv oder negativ sein können, abhängig vom Modell. Die Fehler zeigen (beispielsweise), dass wir den Einfluss der Wolken nicht verstehen ebenso wie alle Prozesse, die deren Entstehung und Auflösung bewirken aufgrund grundlegender physikalischer Prinzipien. Anderenfalls würden alle Modelle in etwa die gleiche Wolkenmenge ergeben“. Bitte kein weiteres Auslassen des mittleren quadratischen Fehlers [root-mean-square-error].

Hier folgt Abbildung 1 bei Roy, welche seinen ersten großen Fehler belegt. Die beweiskräftigen Worte habe ich hervorgehoben:

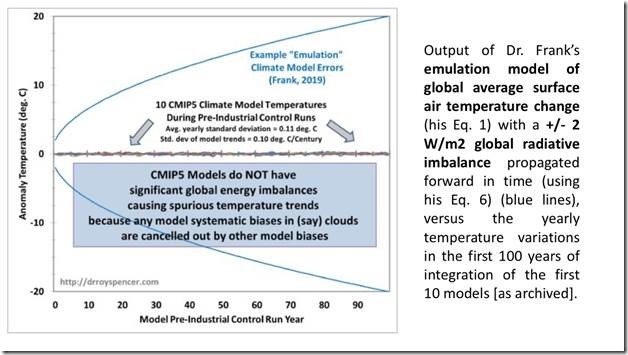
Bildinschrift [rechts]: Ergebnis des nachgebildeten Modells der Änderung der globalen Lufttemperatur von Dr. Frank (seine Gl. 1) mit einem globalen Strahlungs-Ungleichgewicht von ±2 W/m², was sich mit der Zeit fortpflanzt (unter Anwendung seiner Gl. 6; blaue Linien). Dies im Vergleich zu den jährlichen Temperatur-Variationen über die ersten 100 Jahre der ersten 10 Modelle.

Roys blaue Linien sind keine nachgebildeten Lufttemperaturen unter Anwendung von Gleichung 1 aus der Studie. Sie folgen nicht aus Gleichung 1 und repräsentieren überhaupt nicht physikalische Lufttemperaturen.

Sie stammen aus den Gleichungen 5 und 6 und stellen die anwachsenden Unsicherheits-Grenzen dar bei der projizierten Lufttemperatur. Unsicherheits-Statistiken sind keine physikalischen Temperaturen.

Roy hat seine ±2 W/m² als Strahlungs-Ungleichgewicht missverstanden. Im ganzen Zusammenhang meiner Analyse sollte man es sehen als eine ±2 W/m²-Unsicherheit des langwelligen Wolkenantriebs (LWCF). Es ist ein statistischer Wert und kein Energiefluss.

Noch schlimmer: falls wir Roys ±2 W/m² als Strahlungs-Ungleichgewicht in eine Modellsimulation einfließen lassen würden – eine, die zu einem Ausschlag der simulierten Lufttemperatur führt (was Roy meint), dann müssten wir annehmen, dass das Ungleichgewicht gleichzeitig positiv und negativ ist, d. h. ein ±-Strahlungsantrieb.

Ein ±-Strahlungsantrieb alterniert nicht zwischen +-Strahlungsantrieb und –-Strahlungsantrieb. Vielmehr treten beide sofort gleichzeitig auf.

Also folgen aus Roys Interpretation des LWCF-±-Fehlers als ein Ungleichgewicht im Strahlungsantrieb simultan positive und negative Temperaturen.

Man betrachte noch einmal Roys Abbildung. Er zeigt die nachgebildete Lufttemperatur gleichzeitig als ein Heiß-Haus und ein Eis-Haus mit sowohl +20°C als auch -20°C nach 100 Jahren. Das ist die unsinnige Botschaft von Roys blauen Linien, falls wir seine Interpretation übernehmen, dass die ±2 W/m² ein Strahlungs-Ungleichgewicht ist.

Diese physikalisch unmögliche Bedeutung hätte eigentlich schon der grundlegende Hinweis darauf sein müssen, dass die zugrunde liegende Annahme falsch war.

Das ± ist schließlich nicht entweder das Eine oder das Andere, plus oder minus. Es ist zusammenfallend plus und minus, weil es Teil der RMSE-Unsicherheits-Statistik ist. Es wird nicht angewendet auf einen physikalischen Energiefluss.

Es ist wirklich komisch. Mehr als einer von meinen Begutachtern machte den gleichen sehr naiven Fehler, dass ±C = physikalisch real +C oder -C sind. Stellvertretend hierfür das folgende Zitat, was in der Supporting Information erwähnt wird:

„Die Fehlerfortpflanzung des Autors ist physikalisch nicht gerechtfertigt. Beispiel: selbst nach der Stabilisierung der Antriebe, würde die Analyse des Autors ergeben, dass die Modelle sogar noch heftiger zwischen Schneeball und Runaway-Treibhaus-Zuständen hin und her schwingen. Was – und das sollte offensichtlich sein – tatsächlich nicht der Fall ist“.

Hier fehlt eindeutig jedes Verständnis für eine Unsicherheits-Analyse.

Genauso ist auch dieser erste Teil von Roys Punkt 1 vollkommen missverstanden.

Nächster Fehler in der ersten Kritik: Roy sagt, dass die nachgebildete Gleichung nicht die flach verlaufende GCM-Linie aus dem Kontrolllauf in seiner Abbildung 1 spiegelt.

Allerdings würde die nachgebildete Gleichung 1 wirklich die gleiche flache Linie ergeben wie aus den GCM-Kontrollläufen mit Null externem Antrieb. Als Beleg folgt hier Gleichung 1:

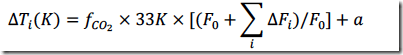
In einem Kontrolllauf gibt es keine Änderung des Antriebs, daher Df_i = 0. Der Term in Klammern wird dann zu F₀/F₀ = 1.

Das auslösende F_CO2 = 0,42, so dass sich Gleichung 1 ergibt zu DT_i(K) = 0,42´33K´1 + a = 13,9 C +a = konstant (a = 273,1 K oder 0°C).

Zieht man eine Anomalie heran, ist die nachgebildete Temperaturänderung konstant Null, genau wie in den GCM-Kontrollläufen in Roys Abbildung 1.

Roys erster Einwand weist also drei Fehler auf:

1) Roy verwechselt einen RMS statistische Unsicherheit im simulierten LWCF als ein physikalisches Strahlungs-Ungleichgewicht.

2) Dann missversteht er eine ±-Unsicherheit der Lufttemperatur als eine physikalische Temperatur.

3) Seine Analyse der nachgebildeten Gleichung 1 war unachtsam.

Weiter mit Punkt 2 von Roy:

Klimamodelle weisen KEINE substantiellen Fehler in ihrem gesamt-Energiefluss an der Obergrenze der Atmosphäre [TOA] auf.

Roy schrieb: „Falls irgendein Klimamodell an der TOA einen Bias des Energieflusses von der Größe von 4 W/m² aufweist, würde sich eine substantielle falsche Erwärmung oder Abkühlung ergeben. Beides ist nicht der Fall“.

Im Folgenden werde ich zeigen, warum dieser Einwand irrelevant ist.

Hier folgt jetzt Roys zweite Abbildung, die wiederum das perfekte Strahlungs-Gleichgewicht der CMIP5-Modelle an der TOA zeigt. Rechts neben Roys Abbildung befindet sich Abbildung 4 aus der Studie, welche den jährlichen Fehler des Gesamtanteils der Wolken in 12 CMIP5-Klimamodellen zeigt, im Mittel ±12,1%. [1]:

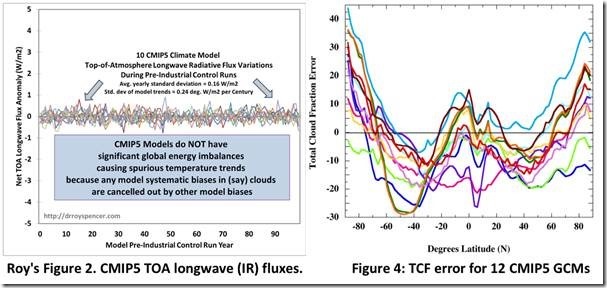
Jedes einzelne der CMIP5-Modelle, welches einen Fehler von ±12,1% des simulierten Gesamt-Wolkenanteils erzeugte, erzeugte auch Roys perfektes Strahlungs-Gleichgewicht an der TOA. Daher erzeugte jedes einzelne CMIP5-Modell, welches einen LWCF-Fehler von gemittelt ±4 W/m² zeigte, ebenfalls das perfekte Strahlungsgleichgewicht an der TOA von Roy.

Wie kann das sein? Wie können Modelle ein perfektes TOA-Gleichgewicht einhalten und gleichzeitig Fehler beim langwelligen Wolkenantrieb erzeugen?

Indem sich Fehler ausmitteln. Von GCMs wird ein TOA-Gleichgewicht gefordert. Also werden die Parameter innerhalb ihrer Unsicherheits-Bandbreite so adjustiert, dass jenes Ergebnis herauskommt.

Roy sagt das auch selbst: „Falls ein Modell in ein globales Energie-Gleichgewicht gezwängt wurde, dann haben sich die Verzerrungen in de Strahlungsfluss-Komponenten herausgemittelt. …“.

Sind die gewählten GCM-Parameterwerte physikalisch korrekt? Das weiß niemand.

Sind die Parameter-Sätze von Modell zu Modell identisch? Nein. Wir wissen das, weil verschiedene Modelle verschiedene Profile erzeugen ebenso wie integrierte Intensitäten des TCF-Fehlers.

Dies nimmt Roys Einwänden bzgl. der TOA jede Grundlage.Modelle zeigen ein TOA-Gleichgewicht und einen LWCF-Fehler gleichzeitig.

In jedem Falle kommt man hier zu dem oben und in der Studie erwähnten Punkt, dass ein simuliertes Klima ein perfektes TOA-Gleichgewicht aufweist, während gleichzeitig der simulierte Klima-interne Energiezustand nicht korrekt ist.

Das bedeutet, dass die den simulierten Klimazustand beschreibende Physik nicht korrekt ist. Und dies wiederum bedeutet, dass die Physik zur Beschreibung der simulierten Lufttemperatur nicht korrekt ist.

Die simulierte Lufttemperatur beruht nicht auf physikalischem Wissen. Und das bedeutet, dass es eine große Unsicherheit bei der projizierten Lufttemperatur gibt, weil wir keine physikalisch gute kausale Erklärung für dieselbe haben.

Das ist die entscheidende Grundlage einer Unsicherheits-Analyse. Man kann die Messgrößen korrekt ermitteln. Aber wenn die falsche Physik die richtige Antwort gibt, hat man nichts gelernt und man versteht nichts. Die Unsicherheit im Ergebnis ist also konsequenterweise groß.

Diese falsche Physik ist in jedem einzelnen Schritt einer Klima-Simulation präsent. Die berechneten Lufttemperaturen fußen nicht auf einer physikalisch korrekten Theorie.

Roy sagt, dass der LWCF-Fehler unbedeutend ist, weil sich alle Fehler gegenseitig ausgleichen. Dazu weiter unten mehr. Aber man beachte, was er sagt: Die falsche Physik gestattet die richtige Antwort. Und das unveränderlich in jedem Schritt einer Projektion über 100 Jahre.

In seiner Kritik vom 12. September liefert Roy seinen Grund, warum er nicht an eine Unsicherheits-Analyse glaubt: „Alle Modelle zeigen die Auswirkungen anthropogener CO₂-Emissionen, trotz bekannter Komponenten ihrer Energieflüsse (wie Wolken)! Warum?

Falls ein Modell in ein globales Energie-Gleichgewicht gezwängt worden ist, dann haben sich die Verzerrungen der Komponenten des Energieflusses herausgemittelt. Belegt wird dies durch die Kontrollläufe der verschiedenen Klimamodelle in ihrem (langwelligen Infrarot-)Verhalten“.

Da haben wir es: eine falsche Physik, die unveränderlich korrekt ist bei jedem Schritt über eine 100-Jahre-Projektion, weil jedwede großmaßstäbliche Fehler sich ausgleichen, um die Auswirkungen kleiner Störungen zu enthüllen. Ich glaube nicht, dass irgendeine andere Fachrichtung der physikalischen Wissenschaft eine solche Behauptung durchgehen lassen würde.

Roy präsentierte dann noch einmal die TOA-Strahlungs-Simulationen links im zweiten Satz der Abbildungen oben.

Er schrieb, dass die Modelle in ein TOA-Gleichgewicht gezwängt werden. Das heißt, der physikalische Fehler, der als TOA-Ungleichgewicht auftauchen würde, würde zwangsweise auf die simulierten Klima-Untersysteme verteilt.

Die Modelle zwangsweise in ein TOA-Gleichgewicht zu bringen kann sogar simulierte Klima-Untersysteme noch fehlerhafter daher kommen lassen als es anderenfalls der Fall wäre.

Nach der Beobachtung, dass das „erzwungene Ausgleichen des globalen Energie-Haushaltes“ nur einmal bei den „vorindustriellen Kontrollläufen über viele Jahrhunderte“ durchgeführt worden war, beobachtete Roy, dass sich die Modelle weltweit ähnlich verhalten, trotz einer „ERHEBLICHEN Vielfalt von Fehlern in den Energiefluss-Komponenten…“

Das ist eine interessante Aussage von Roy angesichts des Umstands, dass es einen Faktor von fast drei gibt in den Unterschieden der Modelle untereinander hinsichtlich ihrer Sensitivität auf eine CO₂-Verdoppelung. [2], [3]

Stephens [3] schreibt: „Weithin glaubt man, dass die Diskrepanz Unsicherheiten bei der Rückkopplung durch Wolken geschuldet ist. … Abbildung 1 zeigt die Änderungen der tiefen Wolken, wie sie von zwei Versionen von Modellen prognostiziert werden, die an jedem Ende der Bandbreite von Erwärmungs-Reaktionen liegen. Die von einem Modell prognostizierte reduzierte Erwärmung ist eine Folge von vermehrter tiefer Bewölkung in jenem Modell, während die verstärkte Erwärmung des anderen Modells auf eine verringerte tiefe Bewölkung zurückzuverfolgen ist“.

Aha! Zwei CMIP5-Modelle zeigen entgegen gesetzte Trends des simulierten Wolken-Anteils als Reaktion auf einen CO₂-Antrieb. Nichtsdestotrotz reproduzieren beide Modelle den historischen Trend der Lufttemperatur.

Nicht nur das, sondern sie sind vermeintlich invariabel korrekt in jedem Schritt der 100-Jahre-Projektion, weil sich ihre großmaßstäblichen Fehler ausgleichen, um die Auswirkungen kleiner Störungen zu enthüllen.

In Stephens Beispielobjekt können wir sehen, wie die versteckte Simulations-Unsicherheit sich manifestiert. Modelle reproduzieren auf Biegen und Brechen Kalibrierungs-Messgrößen und werden mit dieser Grundlage als fähig hinaus posaunt, dass sie zukünftige Klimazustände genau prognostizieren können.

Das Beispiel von Stephens zeigt eindeutig, dass GCMs schlicht und ergreifend nicht die Reaktion der Bewölkung auf CO₂-Emssionen auflösen können. Daher können die GCMs auch nicht die Änderung der Lufttemperatur auflösen, falls diese überhaupt auftreten durch CO₂-Emissionen. Von deren projizierten Lufttemperaturen ist nicht bekannt, dass sie physikalisch korrekt wären. Sie haben keine physikalische Bedeutung.

Dies ist die Ursache der großen und schrittweise zunehmenden Simulations-Unsicherheit bei der projizierten Lufttemperatur.

Dies umgeht Roys Punkt hinsichtlich sich ausgleichender Fehler. Die Modelle können die Reaktion der Wolken auf den CO2-Antrieb nicht auflösen. Das Beseitigen der Fehler bzgl. des Strahlungsantriebs schafft dieses Problem nicht aus der Welt. Eine derartige Beseitigung (mittels händischem Frisierens) versteckt die Simulations-Unsicherheit nur auf trügerische Weise.

Roy folgert: „folglich demonstrieren die Modelle selbst, dass ihre Vorhersagen bzgl. globaler Erwärmung nicht abhängig sind von jenen Bias-Fehlern in den Komponenten der Energieflüsse (wie etwa die globale Wolkenbedeckung), wie von Dr. Frank behauptet“.

Jeder sollte wissen, warum diese Folgerung falsch ist. Sich ausgleichende Fehler machen Modelle einander ähnlich. Sie machen die Modelle aber nicht genauer. Auch werde dadurch nicht physikalische Beschreibungen verbessert.

Roys Folgerung enthüllt implizit seinen Denkfehler.

1) Die Unfähigkeit der GCMs, die Bewölkungs-Reaktion darzustellen bedeutet, dass die Konsistenz von Temperaturprojektionen der Modelle untereinander ein schimärisches Artefakt ihrer Bearbeitung ist. Die Unsicherheit verbleibt in der Projektion, sie ist lediglich verborgen.

Der LWCF-rsme von ±4 W/m² repräsentiert eine Unsicherheit im simulierten Energiefluss. Es ist in keiner Weise ein physikalischer Fehler.

Man kann das Modell frisieren, um überhaupt keinen beobachtbaren Fehler im Kalibrierungs-Zeitraum zu erzeugen (Simulation minus Beobachtung = 0). Aber die der Simulation zugrunde liegende Physik ist falsch. Die Kausalität tritt nicht zutage. Die Simulation vermittelt keine Informationen. Das Ergebnis ist nicht irgendein Indikator physikalischer Genauigkeit. Die Unsicherheit ist nicht beseitigt.

3) Alle Modelle mit jenen Fehlern werden dann erzwungenermaßen in ein TOA-Gleichgewicht gebracht. Jene TOA-gleichgewichteten CMIP5-Modelle machen Fehler von ±12,1% beim globalen TCF [1]. Dies bedeutet, dass die GCMs die Bewölkung nicht mit einer besseren Auflösung simulieren können als mit ±12,1%.

Um die Auswirkungen jährlicher CO₂-Emissionen maximal aufzulösen, müssen sie eine Wolken-Auflösung von etwa 0,1% aufweisen (siehe Anhang 1 unten).

4) Der mittlere GCM-Fehler bei der simulierten TCF über den Kalibrierungs-Zeitraum in der Vergangenheit enthüllt den Kalibrierungs-Fehler des simulierten langwelligen Wolken-Antriebs. Obwohl durchweg ein TOA-Gleichgewicht aufrecht erhalten wird, geht die korrekte Größenordnung des simulierten troposphärischen thermischen Energieflusses innerhalb eines Unsicherheits-Intervalls von ±4 W/m² verloren.

Zu Roys Punkt 3): Das Modell der Fehlerfortpflanzung ist für Klimamodelle nicht geeignet!

Auf seinem Blog schrieb Roy, dass die Modellierung des Klimas in etwa der Modellierung von Kesseln mit heißem Wasser gleicht. Und so: „Falls unser Modell eine konstante Wassertemperatur bekommen kann, wissen wir, dass jene Raten von Energie-Zufuhr und -Verlust gleich sind, obwohl wir deren Werte nicht kennen. Und dass falls wir das Modell mit ein wenig mehr Abdeckung des Topfes durch einen Deckel laufen lassen, wissen wir, dass die modellierte Wassertemperatur zunehmen wird. Jener Teil Physik steckt immer noch im Modell“.

Roy weiter: „Die Temperaturänderung von irgendwas, einschließlich des Klimasystems, ist einem Ungleichgewicht geschuldet zwischen Energiegewinn und Energieverlust des Systems“.

Roy impliziert hier, dass die einzige Möglichkeit einer Temperaturänderung einer Zunahme oder Abnahme der Gesamt-Energie im Klimasystem geschuldet ist. Das ist jedoch nicht richtig.

Klima-Subsysteme können Energie austauschen. Die Lufttemperatur kann sich ändern durch eine Umverteilung interner Energieflüsse ohne jede Änderung der Gesamtenergie, welche in das Klimasystem hinein oder aus demselben wieder hinaus geht.

So sagte beispielsweise Richard Lindzen im Jahre 2001 bei einer Anhörung des Environment and Public Works Committee des US-Senats am 2. Mai: „Behauptungen, wonach der Mensch irgendeinen Anteil an der beobachteten Erwärmung hätte, basieren auf der Hypothese, dass die Modelle die natürliche Variabilität korrekt erfasst haben. Allerdings erfordert die natürliche Variabilität keinerlei externe Antriebe – seien diese nun natürlichen oder anthropogenen Ursprungs [4].

Genau das Gleiche äußerte Lindzen in seinem Beitrag mit dem Titel Some Coolness Concerning Global Warming. [5]:

„Die genaue Ursache der natürlichen Variabilität ist nach wie vor unbekannt, aber das ist keine allzu große Überraschung. Obwohl die in das Erde-Ozean-Atmosphäre-System einfallende Solarstrahlung relativ konstant ist, ist das bei dem Grad, mit dem diese Energie in den Ozeanen gespeichert und wieder freigesetzt wird, nicht der Fall. Folge: Die der Atmosphäre zur Verfügung stehende Energie allein ist alles andere als konstant … tatsächlich war unser Klima schon sowohl wärmer als auch kälter als heute – allein der natürlichen Variabilität des Systems geschuldet. Externe Einflüsse sind für eine derartige Variabilität kaum vonnöten“.

In seiner Begutachtung des Artikels von Stephen Schneider „Laboratory Earth“ beschrieb er diese direkt relevante Beobachtung:

„Eine Verdoppelung des CO₂-Gehaltes in der Atmosphäre führt zu einer Störung des Energie-Gleichgewichts in derselben um zwei Prozent. Aber die Modelle, die zur Prognose der Reaktion der Atmosphäre auf diese Störung herangezogen werden, weisen Fehler in der Größenordnung von zehn Prozent auf hinsichtlich ihrer Repräsentation des Energie-Gleichgewichtes, und diese Fehler involvieren neben Anderem die Rückkopplungen, welche für die resultierenden Berechnungen grundlegend sind. Folglich sind die Modelle kaum brauchbar bei der Abschätzung der klimatischen Reaktionen auf solche feinen Störungen. Außerdem, die starken Reaktionen (korrespondierend mit hoher Sensitivität) der Modelle auf die kleinen Störungen durch eine CO₂-Verdoppelung hängen grundlegend ab von positiven (verstärkenden) Rückkopplungen von Prozessen, die nachweislich von den Modellen ganz falsch repräsentiert werden“.

Diese Beobachtungen sind bereits ausreichend, um Roys Beschreibung der Modellierung von Lufttemperaturen zu widerlegen, analog zu der Wärme, die einem Topf mit kochendem Wasser hinzugefügt und von diesem wieder abgegeben wird – mit unterschiedlich starker Abdeckung durch einen Deckel.

Vor allem der letzte Punkt von Lindzen widerspricht der Behauptung von Roy, dass die Ausmittelung von Simulationsfehlern eine zuverlässige modellierte Reaktion zulässt auf Antriebe oder auf genau projizierte Lufttemperaturen.

Außerdem ist die Lage sehr viel komplexer als Roy es in seiner Analogie mit dem kochenden Wassertopf beschrieben hat. Zum Beispiel, anstatt des einen Deckels in Roys Beispiel ähneln Wolken mehr multiplen Schichten siebartiger Deckel mit variierender Maschenbreite und Dicke, alle in konstanter Bewegung, und keiner davon bedeckt den ganzen Topf.

Die Topf-Modellierung geht dann weiter mit lediglich einer schwachen Darstellung, wo sich die verschiedenen Deckel zu jeder gegebenen Zeit befinden und ohne deren Tiefe oder Porosität vollständig zu verstehen.

Fehlerfortpflanzung: Ist eine mittlere jährliche Zunahme des CO₂-Antriebs um 0,035 W/m² gegeben, beträgt die Zunahme plus Unsicherheit im simulierten troposphärischen thermischen Energiefluss (0,035±4) W/m². Und das alles unter Erhaltung des simulierten TOA-Gleichgewichtes.

Falls man also das Unsicherheits-Intervall für die Lufttemperatur für irgendeinen spezifischen Jahresschritt berechnen will, würde die Obergrenze des Temperatur-Unsicherheitsintervalls aus +4,035 W/m² berechnet, während die Untergrenze des Intervalls -3,9065 W/m² beträgt.

Setzt man dies auf der rechten Seite der Gleichung 5.2 in der Studie ein und setzt man F0 = 33,30 W/m², dann beträgt das Ein-Schritt-Unsicherheitsintervall der simulierten Lufttemperatur +1,68°C/-1,63°C.

Die vom CMIP5 GCM projizierte mittlere Anomalie der Lufttemperatur würde jedoch 0,015°C betragen – und nicht +1,68°C oder -1,63°C.

Bei der gesamten Modellierung bleibt das simulierte TOA-Gleichgewicht erhalten, hauptsächlich deswegen, weil der Simulationsfehler des langwelligen Wolkenantriebs ausgeglichen wird durch Simulationsfehler beim kurzwelligen Wolkenantrieb.

Dies bedeutet, dass die zugrunde liegende Physik falsch ist und auch der simulierte Klima-Energie-Status falsch ist. Im Nachhinein wird die beobachtete Lufttemperatur im Kalibrierungs-Zeitraum nur wegen der Anpassung der Kurve nach den händisch angebrachten Adjustierungen der Modellparameter korrekt reproduziert [2, 7]

Erzwungene Korrespondenz mit einem bekannten Wert beseitigt nicht die Unsicherheit in einem Ergebnis, weil die kausale Ignoranz ungelöst bleibt.

Wenn Fehler in einem Zwischenergebnis auf jeden einzelnen Schritt einer Reihe von Berechnungen auftreten – was eine Projektion der Lufttemperatur beschreibt – dann setzen sich diese Fehler im nächsten Schritt fort. Der nächste Schritt fügt dann noch seinen eigenen Fehler hinzu. Der einzige Weg, den Effekt der schrittweisen Fehler zu beurteilen ist die schrittweise Fortpflanzung der angemessenen rmse-Unsicherheit.

Abbildung 3 unten zeigt das Problem graphisch dargestellt. GCMs projizieren die Temperatur in einer schrittweisen Abfolge von Berechnungen [8]. Falsche Physik bedeutet, dass jeder Schritt fehlerhaft ist. Der Klima-Energie-Zustand ist falsch.

Der falsche Klimazustand setzt sich dann in den Berechnungen fort. Dessen Fehler legen die initialen Bedingungen des nächsten Schrittes fest. Falsche Physik bedeutet, dass der nächste Schritt seine eigenen Fehler erzeugt. Diese neuen Fehler addieren sich zu denen der initialen Bedingungen. Und so geht es immer weiter, Schritt für Schritt. Die Fehler addieren sich mit jedem Schritt.

Wenn man einen zukünftigen Zustand berechnet, kennt man nicht das Signal oder die Größenordnung von irgendeinem der Fehler im Ergebnis. Dieses Unwissen beruht auf der offensichtlichen Schwierigkeit, dass aus einem zukünftigen Klima keine Messungen vorliegen.

Die Kalibrierungs-Fehlerstatistik informiert uns über die Genauigkeit eines jeden rechnerischen Schrittes einer Simulation. Wenn Ungenauigkeit in jedem Schritt präsent ist, setzt sich die Metrik des Kalibrierungs-Fehlers durch jeden Schritt fort. Damit ergibt sich die Unsicherheit im Ergebnis – also wie groß unser Vertrauen in die Richtigkeit der Zahl ist.

Involviert die Berechnung multiple Einzelschritte, von denen jeder seinen eigenen Fehler beiträgt, dann setzt sich die schrittweise Unsicherheits-Statistik durch die Abfolge der einzelnen Schritte fort. Die Unsicherheit des Ergebnisses muss immer größer werden. Diesen Umstand zeigt Abbildung 3:

Abbildung 3: Zunahme der Unsicherheit einer Projektion der Lufttemperatur. C₀^F,T ist der Grundzustand des Klimas, welcher einen initialen Antrieb F₀ aufweist, der Null sein kann, und eine initiale Temperatur T₀. Die finale Temperatur T_n wird festgelegt durch die finale Unsicherheit ±e_t als T_n±e_t.

Schritt eins projiziert einen Antrieb im ersten Schritt F₁, welcher eine Temperatur T₁ erzeugt. Falsche Physik bringt einen physikalischen Fehler e₁ in die Temperatur ein, der positiv oder negativ sein kann. Bei einer Projektion eines zukünftigen Klimas kennen wir nicht das Signal oder die Größenordnung von e₁.

Allerdings geben uns Kalibrierungs-Experimente im Nachhinein darüber Aufschluss, dass Einzelschritte bei der Projektion eine mittlere Unsicherheit von ±e aufweisen.

T₁ enthält also eine Unsicherheit von T₁±e_r1.

Die Temperatur von Schritt 1 plus deren physikalischer Fehler, T₁+e₁ geht in Schritt 2 als Ausgangsbedingung ein. Aber T₁ wies einen Fehler auf, nämlich e₁. Dieses e₁ ist ein Fehler-Ausgleich eines unbekannten Signals in T₁. Daher erhält die falsche Physik von Schritt 2 eine T₁, die von e₁ ausgeglichen wird. Aber bei Zukunfts-Projektionen kennt man nicht den Wett von T₁+e₁.

In Schritt 2 beginnt die falsche Physik mit der unrichtigen T₁ und fügt einen neuen unbekannten physikalischen Fehler e₂ zu T₂ hinzu. Der Fehler in T₂ beträgt jetzt e₁+e₂. Allerdings bleiben in einer Zukunfts-Projektion Signal und Größenordnung von e₁, e₂ und deren Summe unbekannt.

Und so geht es immer weiter – Schritt 3, … n addieren alle ihre jeweiligen Fehler e₃+ … +e_n. Aber weil Signal und Größenordnung der Fehler unbekannt sind, kennen wir auch nicht den Gesamtfehler im finalen Zustand. Alles, was wir wissen ist, dass die Trajektorie des simulierten Klimas sich entfernt hat von der Trajektorie des physikalisch korrekten Klimas.

Die Kalibrierungs-Fehlerstatistik erlaubt jedoch eine Abschätzung der Unsicherheit in den Ergebnissen irgendeines Einzel-Berechnungsschrittes, also ±e.

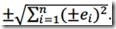[9 bis 11].

Es sollte jedermann völlig klar sein, dass die rss-Gleichung keine physikalischen Temperaturen ergibt oder die physikalischen Größenordnungen von irgendetwas Anderem. Es ist lediglich eine Statistik der prognostischen Unsicherheit, die notwendigerweise mit der Anzahl der Berechnungsschritte der Prognose zunimmt. Eine Zusammenfassung der Literatur bzgl. Unsicherheit habe ich in meinem ursprüngliche Beitrag behandelt.

Die Zunahme der Unsicherheit bedeutet nicht, dass die projizierte Lufttemperatur sehr hoch wird. Projizierte Temperaturen liegen immer zwischen irgendwelchen physikalischen Grenzen. Aber die Zuverlässigkeit jener Temperatur – unser Vertrauen darin, dass sie physikalisch korrekt ist – vermindert sich mit jedem Schritt. Das Vertrauensniveau ist die Bedeutung von Unsicherheit. Mit dem schwindenden Vertrauen nimmt die Unsicherheit zu.

Die Zunahme der Unsicherheit bedeutet, dass wir mit jedem Schritt weniger und immer weniger wissen, wie das simulierte zukünftige Klima nun ist relativ zum physikalisch korrekten zukünftigen Klima. Abbildung 3 zeigt die immer breiter werdende Unsicherheit mit der Anzahl der Schritte.

Darum ist die Fortpflanzung von Unsicherheiten bei einer Projektion der Lufttemperatur vollkommen angemessen. Es ist unsere einzige Abschätzung der Zuverlässigkeit eines prognostischen Ergebnisses.

Anhang 1 unten zeigt, dass die Modelle Wolken bis zu einer Genauigkeit von ±0,1% simulieren müssen, also etwa 100 mal besser als die heutigen ±12,1%, um irgendwelche möglichen Effekte eines CO₂-Antriebs aufzulösen.

Anhang 2 zitiert Richard Lindzen über die totale Korruption und Unehrlichkeit, welche die gesamte AGW-Konsens-Klimatologie durchzieht.

Bevor es weitergeht, folgt hier eine Aussage der NASA zu Wolken und Auflösung: „Bei einer Verdoppelung des atmosphärischen Kohlendioxid-Gehaltes, zu welchem es den Prognosen zufolge während der nächsten 50 bis 100 Jahre kommen soll, wird erwartet, dass sich das Strahlungs-Gleichgewicht an der Erdoberfläche lediglich um etwa 2% ändert. … Falls eine Änderung um 2% wirklich so bedeutsam ist, dann muss ein Klimamodell, um brauchbar zu sein, auf irgendetwas um 0,25% genau sein. Folglich müssen die heutigen Modelle um etwa das Hundertfache an Genauigkeit verbessert werden, eine sehr große Herausforderung“.

Falls Klimamodelle die Reaktion der Wolken auf CO₂-Emissionen nicht auflösen können, dann können sie auch unmöglich die Auswirkung von CO₂-Emissionen auf die Lufttemperatur projizieren.

Die Unsicherheit von ±4 W/m² beim LWCF ist eine direkte Reflektion der ausgeprägten Ignoranz um die Reaktion der Bewölkung.

Die LWCF-Kalibrierungs-Unsicherheit in den CMIP5 reflektiert Ignoranz hinsichtlich der Größenordnung des thermischen Flusses in der simulierten Troposphäre, welcher eine direkte Konsequenz der Unfähigkeit der CMIP5-Modelle ist, den Wolkenanteil zu simulieren.

Der jährliche mittlere CO₂-Antrieb von 0,035 W/m² ist genau ein solcher kleinerer energetischer Effekt. Es ist unmöglich, die Auswirkung einer Änderung des Antriebs von 0,035 W/m² auf die Lufttemperatur aufzulösen, wenn das Modell den troposphärischen Antrieb nicht genauer als ±4 W/m² auflösen kann. Die Durchdringung ist um ±114 Male kleiner als die untere Grenze der Auflösung in einem CMIP5-Modell. Das Unsicherheits-Intervall kann angemessen analogisiert werden als die kleinste Pixelgröße der Simulation. Es ist das Unschärfe-Niveau. Es ist die Breite der Unwissenheits-Bandbreite, innerhalb derer man nichts weiß.

Unsicherheit ist kein physikalischer Fehler. Sie subtrahiert sich nicht hinweg. Sie ist eine Maßzahl von Unwissen.

Das Modell kann eine Zahl erzeugen. Wenn die physikalische Unsicherheit groß ist, dann ist diese Zahl physikalisch bedeutungslos.

All dies wird in der Studie angesprochen, sehr detailliert in Abschnitt 10 der Begleitinformationen. Es ist nicht so, dass die Analyse fehlt oder kryptisch ist. Sie ist jedoch nicht Gegenstand meiner Kritik.

Kleinere seltsame und irrige Gedanken:

Roy schrieb: „Falls ein Modell tatsächlich ein Ungleichgewicht des Energieflusses an der TOA von +4 W/m² aufweist, würde dieser Bias mit der Zeit relativ konstant bleiben“.

Aber der LWCF-Fehler in der Statistik beträgt ±4 W/m² und nicht (+)4 W/m². Hier hat Roy eine Kalibrierungs-Fehlerstatistik nicht nur als einen Energiefluss missverstanden, sondern hat auch den irrigen Gedanken ausgenutzt, um das ± in ein (+) umzuwandeln.

Dieser Fehler ist auch unter meinen vorherigen Begutachtern weit verbreitet. Er erlaubt es ihnen, einen konstanten Ausgleichs-Fehler [offset error] anzunehmen. Und dies wiederum erlaubte es ihnen anzunehmen, dass sich der gesamte Fehler hinweg subtrahiert.

Diese Vermutung der Perfektion nach der Subtraktion ist gängiger Glaube unter den Konsens-Klimatologen. Sie wird direkt vor ihren Augen durch ihre eigenen Ergebnisse widerlegt (Abbildung 1 in [13]), aber das scheint nie eine Rolle zu spielen.

Ein weiteres Beispiel enthält Abbildung 1 in der Studie, welche simulierte Temperatur-Anomalien zeigt. Sie alle werden erzeugt, indem eine simulierte climate base-state-temperature [?] subtrahiert wird. Falls die Simulationsfehler hinweg subtrahiert werden, würden sich alle Anomalietrends überlagern. Aber sie sind von diesem ideal weit entfernt.

Abbildung 4 zeigt ein CMIP5-Beispiel der gleichen Widerlegung:

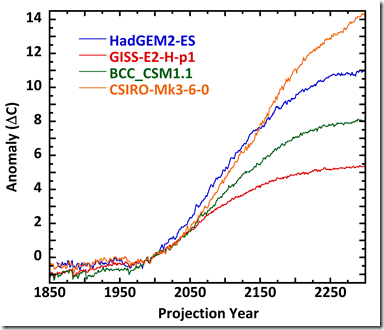
Abbildung 4: RCP8.5-Projektionen von vier CMIP5-Modellen.

Der Gedanke, dass sich Fehler in Anomalien hinweg subtrahieren, ist objektiv falsch. Die Unsicherheiten, welche in den Projektionen nach dem Jahr 2000 versteckt sind, finden sich auch im Zeitraum 1850 bis 2000.

Ursache hierfür ist, dass die Projektionen historischer Temperaturen auf der gleichen falschen Physik basieren wie die Zukunfts-Projektionen. Obwohl die Messgrößen reproduziert werden, wird die dem Temperaturtrend zugrunde liegende physikalische Kausalität vom Modell kaum beschrieben. Der Gesamt-Wolkenanteil wird im Jahre 1950 genauso falsch simuliert wie im Jahre 2050.

Der LWCF-Fehler ist in allen Simulationen präsent. Die mittlere jährliche Simulations-Unsicherheit von ±4 W/m² beim troposphärischen thermischen Energiefluss ist durchweg vorhanden, was in jeden Simulationsschritt der Lufttemperatur Unsicherheit hinein bringt. Das Frisieren der Modelle, um die Messgrößen zu reproduzieren, versteckt die Unsicherheit bloß.

Roy schrieb: „Ein weiterer komischer Aspekt von Gl. 6 ist, dass sie weit unterschiedliche Ergebnisse erzeugen wird, abhängig von der Länge des angenommenen Zeitschrittes.“.

Aber natürlich würde Gl. 6 keine weit unterschiedlichen Ergebnisse erzeugen, weil der Simulationsfehler mit der Länge des Zeitschrittes im GCM variiert.

Zum Beispiel können wir die mittlere Pro-Tag-Unsicherheit aus der jährlichen mittleren Kalibrierung von ±4 W/m² nach Lauer und Hamilton abschätzen.

Roy schloss mit den Worten: „Ich wäre froh, widerlegt zu werden“.

Sei froh, Roy!

[Es folgt jetzt ein Anhang, in denen das oben Gesagte noch detaillierter ausgeführt wird. Auf die Übersetzung wird daher hier verzichtet. Anhang 2 unten wird aber wieder übersetzt, weil er ein längeres und interessantes Zitat von Richard Lindzen enthält. Anm. d. Übers.]

Anhang 1

Appendix 1: Why CMIP5 error in TCF is important.

We know from Lauer and Hamilton that the average CMIP5 ±12.1% annual total cloud fraction (TCF) error produces an annual average ±4 Wm^-2 calibration error in long wave cloud forcing. [14]

We also know that the annual average increase in CO₂ forcing since 1979 is about 0.035 Wm^-2 (my calculation).

Assuming a linear relationship between cloud fraction error and LWCF error, the ±12.1% CF error is proportionately responsible for ±4 Wm^-2 annual average LWCF error.

Then one can estimate the level of resolution necessary to reveal the annual average cloud fraction response to CO₂ forcing as:

[(0.035 Wm^-2/±4 Wm^-2)]*±12.1% total cloud fraction = 0.11% change in cloud fraction.

This indicates that a climate model needs to be able to accurately simulate a 0.11% feedback response in cloud fraction to barely resolve the annual impact of CO₂ emissions on the climate. If one wants accurate simulation, the model resolution should be ten times small than the effect to be resolved. That means 0.011% accuracy in simulating annual average TCF.

That is, the cloud feedback to a 0.035 Wm^-2 annual CO₂ forcing needs to be known, and able to be simulated, to a resolution of 0.11% in TCF in order to minimally know how clouds respond to annual CO₂ forcing.

Here’s an alternative way to get at the same information. We know the total tropospheric cloud feedback effect is about -25 Wm^-2. [15] This is the cumulative influence of 67% global cloud fraction.

The annual tropospheric CO₂ forcing is, again, about 0.035 Wm^-2. The CF equivalent that produces this feedback energy flux is again linearly estimated as (0.035 Wm^-2/25 Wm^-2)*67% = 0.094%. That’s again bare-bones simulation. Accurate simulation requires ten times finer resolution, which is 0.0094% of average annual TCF.

Assuming the linear relations are reasonable, both methods indicate that the minimal model resolution needed to accurately simulate the annual cloud feedback response of the climate, to an annual 0.035 Wm^-2 of CO₂ forcing, is about 0.1% CF.

To achieve that level of resolution, the model must accurately simulate cloud type, cloud distribution and cloud height, as well as precipitation and tropical thunderstorms.

This analysis illustrates the meaning of the annual average ±4 Wm^-2 LWCF error. That error indicates the overall level of ignorance concerning cloud response and feedback.

The TCF ignorance is such that the annual average tropospheric thermal energy flux is never known to better than ±4 Wm^-2. This is true whether forcing from CO₂ emissions is present or not.

This is true in an equilibrated base-state climate as well. Running a model for 500 projection years does not repair broken physics.

GCMs cannot simulate cloud response to 0.1% annual accuracy. It is not possible to simulate how clouds will respond to CO₂ forcing.

It is therefore not possible to simulate the effect of CO₂ emissions, if any, on air temperature.

As the model steps through the projection, our knowledge of the consequent global air temperature steadily diminishes because a GCM cannot accurately simulate the global cloud response to CO₂ forcing, and thus cloud feedback, at all for any step.

It is true in every step of a simulation. And it means that projection uncertainty compounds because every erroneous intermediate climate state is subjected to further simulation error.

This is why the uncertainty in projected air temperature increases so dramatically. The model is step-by-step walking away from initial value knowledge, further and further into ignorance.

On an annual average basis, the uncertainty in CF feedback is ±144 times larger than the perturbation to be resolved.

The CF response is so poorly known, that even the first simulation step enters terra incognita.

Anhang 2: Über Korruption und Unehrlichkeit in der Konsens-Klimatologie

Die außerordentliche Art und Weise, in der Richard Lindzen den Dschungel von Unehrlichkeit, der die Konsens-Klimatologie nun einmal ist, sollte man unbedingt lesen. Keiner der Akademiker, die er namentlich als Teilhaber an den Schikanen nennt, verdient es, als Wissenschaftler weiter beschäftigt zu werden [6].

Falls man seine Kommentierung seit den frühesten Tagen bis heute verfolgt, wird seine Entmündigung [als Wissenschaftler] schmerzlich und offensichtlich [4 bis 7, 16, 17]. Sein Beitrag „Climate Science: Is it Currently Designed to Answer Questions?“ sollte man in ganzer Länge lesen!

—————————–

References:

[1] Jiang, J.H., et al., Evaluation of cloud and water vapor simulations in CMIP5 climate models using NASA “A-Train” satellite observations. J. Geophys. Res., 2012. 117(D14): p. D14105.

[2] Kiehl, J.T., Twentieth century climate model response and climate sensitivity. Geophys. Res. Lett., 2007. 34(22): p. L22710.

[3] Stephens, G.L., Cloud Feedbacks in the Climate System: A Critical Review. J. Climate, 2005. 18(2): p. 237-273.

[4] Lindzen, R.S. (2001) Testimony of Richard S. Lindzen before the Senate Environment and Public Works Committee on 2 May 2001. URL: http://www-eaps.mit.edu/faculty/lindzen/Testimony/Senate2001.pdf Date Accessed:

[5] Lindzen, R., Some Coolness Concerning Warming. BAMS, 1990. 71(3): p. 288-299.

[6] Lindzen, R.S. (1998) Review of Laboratory Earth: The Planetary Gamble We Can’t Afford to Lose by Stephen H. Schneider (New York: Basic Books, 1997) 174 pages. Regulation, 5 URL: https://www.cato.org/sites/cato.org/files/serials/files/regulation/1998/4/read2-98.pdf Date Accessed: 12 October 2019.

[7] Lindzen, R.S., Is there a basis for global warming alarm?, in Global Warming: Looking Beyond Kyoto, E. Zedillo ed, 2006 in Press The full text is available at: https://ycsg.yale.edu/assets/downloads/kyoto/LindzenYaleMtg.pdf Last accessed: 12 October 2019, Yale University: New Haven.

[8] Saitoh, T.S. and S. Wakashima, An efficient time-space numerical solver for global warming, in Energy Conversion Engineering Conference and Exhibit (IECEC) 35th Intersociety, 2000, IECEC: Las Vegas, pp. 1026-1031.

[9] Bevington, P.R. and D.K. Robinson, Data Reduction and Error Analysis for the Physical Sciences. 3rd ed. 2003, Boston: McGraw-Hill.

[10] Brown, K.K., et al., Evaluation of correlated bias approximations in experimental uncertainty analysis. AIAA Journal, 1996. 34(5): p. 1013-1018.

[11] Perrin, C.L., Mathematics for chemists. 1970, New York, NY: Wiley-Interscience. 453.

[12] Roy, C.J. and W.L. Oberkampf, A comprehensive framework for verification, validation, and uncertainty quantification in scientific computing. Comput. Methods Appl. Mech. Engineer., 2011. 200(25-28): p. 2131-2144.

[13] Rowlands, D.J., et al., Broad range of 2050 warming from an observationally constrained large climate model ensemble. Nature Geosci, 2012. 5(4): p. 256-260.

[14] Lauer, A. and K. Hamilton, Simulating Clouds with Global Climate Models: A Comparison of CMIP5 Results with CMIP3 and Satellite Data. J. Climate, 2013. 26(11): p. 3823-3845.

[15] Hartmann, D.L., M.E. Ockert-Bell, and M.L. Michelsen, The Effect of Cloud Type on Earth’s Energy Balance: Global Analysis. J. Climate, 1992. 5(11): p. 1281-1304.

[16] Lindzen, R.S., Climate Science: Is it Currently Designed to Answer Questions?, in Program in Atmospheres, Oceans and Climate. Massachusetts Institute of Technology (MIT) and Global Research, 2009, Global Research Centre for Research on Globalization: Boston, MA.

[17] Lindzen, R.S., Can increasing carbon dioxide cause climate change? Proc. Nat. Acad. Sci., USA, 1997. 94(p. 8335-8342

Link: https://wattsupwiththat.com/2019/10/15/why-roy-spencers-criticism-is-wrong/

Übersetzt von Chris Frey EIKE

Mit Klimaschutz zum Sozialismus, und dann wird die Natur geschrottet

geschrieben von AR Göhring | 22. Oktober 2019

Von Interesse ist freilich, warum es geht. Was genau bringt die sich immer mehr aufschaukelnde Klimahysterie in unseren Tagen zustande, was setzt die Massen in Aktion? Sind es säkulare Erlösungsbedürfnisse, die an den Platz der religiösen getreten sind? Oder pubertäre Allmachtphantasien, die nach einem Ventil suchen? Handelt es sich um eine Erscheinungsform des Generationenkonflikts, ähnlich wie zu den Zeiten der 1968er? Oder stecken raffinierte Macht- und Gewinninteressen dahinter? Wahrscheinlich sind all diese Faktoren beteiligt, wie denn die meisten Ereignisse nicht nur eine, sondern viele Ursachen haben, die erst durch ihr Zusammenwirken den beobachteten Effekt erzielen.

Bei dieser kurzen Tour d’Horizon bleibt indessen ein Gesichtspunkt unberücksichtigt, der besondere Aufmerksamkeit verdient. Wer die Äußerungen der Klimabewegten nämlich verfolgt, wird schnell bemerken, dass sie bei aller Verschiedenheit in einem Punkt unisono übereinstimmen: Der eigentlich Verantwortliche für den „menschengemachten Klimawandel“ ist nach ihrer Auffassung „der Kapitalismus“, also die Marktwirtschaft. Das aktuelle Gewinninteresse einiger weniger, so der allgemeine Tenor, wirke dahin, dass die Welt von morgen mit Wirkung für alle ruiniert werde. Der Kapitalismus erscheint auf diese Weise als Menschheitsfeind Nummer eins. Die folgerichtige Konsequenz dieser Hypothese ist die, dass eine wirksame Abhilfe nur durch den Sozialismus, das heißt durch Planwirtschaft und überhaupt durch die Vergesellschaftung aller menschlichen Beziehungen erfolgen kann.

Die Auseinandersetzung zwischen Kapitalismus und Sozialismus ist daher ein integraler Bestandteil der gegenwärtigen Klimadebatte. Ja, diese ist geradezu die Form, in der sich der sozialistische Gedanke erneut anschickt, die Welt zu erobern, nachdem er mit dem Ende des Ostblocks Schiffbruch erlitten hat. So gesehen, passt es recht gut ins Bild, dass sich Greta Thunberg, die kindliche Ikone der Klimabewegung, zur Freude aller „Antifaschisten“ in einem T-Shirt mit dem Aufdruck „Antifascist“ hat abbilden lassen. Eine deutlichere Parteinahme für den Sozialismus lässt sich schwer vortstellen. Sozialismus oder Weltuntergang, lautet dementsprechend der Weckruf, mit dem die Völker abermals zum letzten Gefecht aufgerufen werden sollen. Die Antwort steht bei dieser Gegenüberstellung bereits fest, denn erst kommt selbstverständlich das Überleben, dann erst alles übrige.

Fatale Klimabilanz des realen Sozialismus

Wer den Sozialismus noch aus der Nähe besichtigen durfte, weiß nicht, ob er wach ist oder träumt. Die sozialistischen Staaten hatten die schlechteste Umweltbilanz weltweit. Die Erreichung der vorgegebenen Planziele ließen es für die verantwortlichen Politiker gar nicht zu, an kostenintensive Umweltschutzmaßnahmen zu denken. Umweltschutz hätte bedeutet, die Produktionskosten zu erhöhen und damit die Produktivität der sozialistischen Wirtschaft noch weiter zu verringern. Das hätte die marxistische Verheißung einer Überflussproduktion, die Wohlstand für alle garantiert, vollends desavouiert.

Aus der Mitte der Bevölkerung konnte kein Gegendruck aufgebaut werden, weil die staatlich gelenkten Medien dies nicht zuließen. Wer daher Gelegenheit hatte, bei Halle und Merseburg an den Leuna- und Bunawerken vorbeizufahren – gewöhnlichen Transitreisenden war dies verwehrt, weil sie die Transitstrecken bei Strafe nicht verlassen durften –, konnte gelegentlich kaum die Hand vor den Augen sehen. Ein an der Universität Halle beschäftigter Mediziner berichtete mir Anfang der 80er Jahre, die schweren Atemwegserkrankungen der dortigen Arbeiter seien den Fachleuten sehr wohl bekannt. Man wusste, dass der Produktionsbetrieb dringend hätte modernisiert werden müssen, Filter eingebaut und so weiter. Diese Dinge mussten jedoch streng unter Verschluss gehalten werden und durften aus politischen Gründen auf keinen Fall an die Öffentlichkeit gelangen. Es war ein Teufelskreis, der nur mit einem Eklat enden konnte.

Nach dem Fall der Mauer und dem Ende des realen Sozialismus in Europa gingen die umweltschädlichen Emissionen rasch auf ein in den kapitalistischen Staaten übliches Maß zurück. Die Einführung kapitalistischer Produktionsmethoden hatte also keine Verschlechterung, sondern genau umgekehrt eine signifikante Verbesserung der Umweltbilanz zur Folge. Spricht man Klimaaktivisten darauf an, erhält man gewöhnlich zur Antwort, der reale Sozialismus des früheren Ostblocks sei kein „wahrer Sozialismus“ gewesen. In einem solchen verhalte es sich nämlich ganz anders. Diese Argumentation hat Tradition. Sie erinnert verblüffend an die Auskunft, die man früher erhielt, wenn man darauf hinwies, dass es den Arbeitern im sozialistischen Arbeiterparadies um vieles schlechter gehe als ihren ausgebeuteten Kollegen im kapitalistischen Westen, und zwar so sehr, dass sie nur durch Mauer und Stacheldraht am Weglaufen gehindert werden konnten. Auch hier hieß es, dass dies eben kein „wahrer Sozialismus“ sei; man müsse es besser machen. Wenn der Sozialismus erst richtig verwirklicht sei – und zwar weltweit, sonst könne er sich nicht zu voller Blüte entfalten –, verhalte sich alles genau umgekehrt.

Die Umweltbewegung kam wie gerufen

Ideologien haben es bekanntlich an sich, dass sie den Blick auf die Realität partiell verstellen. Sie filtern aus, was dem gewünschten Bild widerspricht, und färben den Rest so ein, dass die wahrgenommene Realität mit der Ideologie übereinstimmt. Wenn es gar nicht anders geht, wird die Ideologie unter Beibehaltung ihrer Grundstruktur ein wenig umformuliert. Das lässt sich an der Entwicklung des Sozialismus gut beobachten. Nachdem sich erwiesen hatte, dass die Arbeiter für die Weltrevolution nicht zu gewinnen waren, wurde das Ziel der Vergesellschaftung aller Verhältnisse keineswegs aufgegeben.

Vielmehr wandte sich der Sozialismus von der Arbeiterbefreiung allmählich ab und hielt nach anderen publikumswirksamen Zukunftsvisionen Ausschau. Da kam die durch den Club of Rome forcierte Umweltbewegung wie gerufen, denn diese hatte kein geringeres Anliegen, als den Globus vor dem menschengemachten Untergang zu retten. Unter den „Grünen“, die sich dieses Ziel zu eigen machten, fanden sich anfangs Akteure sehr unterschiedlicher Couleur zusammen. Im Ergebnis jedoch dominierten die Anhänger der K-Gruppen, weshalb die Grünen auch als Kürbispartei bezeichnet wurden: außen grün, aber innen rot und auf die Revolutionierung aller Verhältnisse aus. Die Melange aus neo-marxistischen Revolutionären und Umweltaktivisten erwies sich als zukunftsträchtig, die ökosozialistische Rettung der Welt vor dem drohenden Untergang avancierte zur neuen Form der sozialistischen Welteroberung.

Das ist gut an dem Wanderer zwischen den Welten Rudolf Bahro zu beobachten, der sich als Emigrant aus der DDR im Westen intensiv bemühte, die ökologische mit der sozialistischen „Sache“ zu verbinden. Aber auch in den sozialistischen Staaten selbst war man sich der Chance, die sich hier auftat, bewusst. Die DDR-Nomenklatura ließ ungescheut verlauten, dass nur die gesamtgesellschaftliche Planung der Produktion die Umweltprobleme lösen könnte. Nachdrücklich warb auch der DDR-Philosoph Wolfgang Harich für einen „Kommunismus ohne Wachstum“, der an die Stelle des von Marx verheißenen Reichs des allgemeinen Überflusses treten sollte: „Ein dem Überfluß abschwörender Kommunismus wäre die Lösung, auf die Naturschützer, Nostalgiker und geschlagene, mutlos gewordene Neue Linke sich … einigen könnten …“

Anstelle der Rettung der ausgebeuteten Arbeiterschaft wurde hier kurzerhand die Rettung des ausgebeuteten Globus zum Movens der sozialistischen Bewegung ins Auge gefasst. Damit ist freilich die Frage, warum genau die sozialistische Planwirtschaft dafür besser geeignet sein sollte als die kapitalistische Wettbewerbswirtschaft, noch nicht beantwortet. Wie Harichs Gesprächspartner festhielt, war Harichs Zielvorstellung „gewiß der totale Polizeistaat globaler Versorgung, den er offenbar bejaht“. Der ungehinderte obrigkeitliche Durchgriff war also der Grund, weshalb der Sozialismus dem bürgerlichen Rechtsstaat als überlegen angesehen wurde.

Umfassende Vergesellschaftung als Selbstzweck

Die hier sichtbar werdende ökologische Anreicherung des sozialistischen Zentralismus und Bürokratismus findet eine überraschende Bestätigung in dem Buch „Das Prinzip Verantwortung“ von Hans Jonas, das an sich gegen die sozialistischen Zukunftsvisionen Ernst Blochs gerichtet war. Aber ungewollt zeigt sich der Ökosozialismus hier in seiner wahren Gestalt. Denn wie Jonas darlegt, komme zu den, „im ganzen doch wohl besseren, Chancen für einen Geist der Rationalität in einer sozialistischen Gesellschaft“ hier noch „die größere Macht, ihn praktisch auch durchzusetzen und zu seinen Gunsten auch das Unpopuläre aufzuerlegen … Die Entscheidungen der Spitze, die ohne vorherige Zustimmung von Unten getroffen werden können, stoßen auf keinen Widerstand im Sozialkörper … und können bei einiger Zuverlässigkeit des Apparats der Ausführung sicher sein. Das schließt Maßnahmen ein, die das Eigeninteresse der Betroffenen sich spontan nicht auferlegt hätte, die demnach, wenn sie die Majorität treffen, im demokratischen Prozeß schwer zum Beschluß gebracht werden können. Solche Maßnahmen sind aber eben das, was die drohende Zukunft verlangt und immer mehr verlangen wird. Soweit also handelt es sich um die Regierungsvorteile einer jeden Tyrannis, die in unserem Zusammenhang eben eine wohlwollende, wohlinformierte und von der richtigen Erkenntnis beseelte Tyrannis sein muß.“

Was hier nur in Gedanken konzipiert wurde, soll heute real durchgezogen werden. Hysterisierte Massen, von gleichgerichteten Medien ideologisch aufgeladen und von der Dringlichkeit ihrer Mission überzeugt, fordern „CO₂-Steuern“ und andere planwirtschaftliche Maßnahmen, um die Welt im letzten Moment doch noch zu retten. Demokratie und Rechtsstaatlichkeit sind für die Klimabewegten nur etwas für Schönwetterzeiten, in Krisenzeiten jedoch sind sie nicht hilfreich.

Deshalb wird jede Opposition gegen die von den Klimaaktivisten errichtete Meinungsfront diabolisiert. Bis zu welchen Höhen sich der Hass gegen Andersdenkende aufschaukeln kann, hat vor wenigen Jahren ein Grazer Hochschullehrer demonstriert, der für „Klimaleugner“ allen Ernstes öffentlich die Todesstrafe gefordert hat. Diese sei „eine angemessene Sanktion für einflussreiche Klimaleugner“. („I am going to suggest that the death penalty is an appropriate punishment for influential Global Warming deniers.“)

Obwohl er, wie er sagte, an sich ein Gegner der Todesstrafe sei, gehe es hier doch um eine andere Kategorie, nämlich nicht darum, Vergeltung für ein in der Vergangenheit liegendes Delikt zu üben, sondern um ein künftiges Übel, nämlich Millionen, wenn nicht Milliarden von Klimatoten vorausschauend zu verhindern. Das sei lebenserhaltend und verdiene daher eine andere Beurteilung. („… to achieve that goal I think it is justified for a view heads to roll.“) Wem käme hier nicht Schillers Wort in den Sinn, dass „der schrecklichste der Schrecken … der Mensch in seinem Wahn“ ist? Zwar steht die reale Vaporisierung der „Klimaleugner“ nicht auf der offiziellen Tagesordnung. Aber der soziale Tod ist ihnen in dem von vielen geforderten Klimastaat so sicher wie das Amen in der Kirche.

Das sozialistische Chamäleon

Sieht man das Ganze aus der gehörigen Distanz, so ist leicht zu erkennen, dass das sozialistische Chamäleon sich aus zwei Bestandteilen zusammensetzt: einer zugkräftigen Zukunftsvorstellung und einer diese ergänzenden bürokratischen Herrschaftsordnung. Die Zukunftsvorstellung ist der austauschbare Köder, mit dem die Massen mobilisiert werden: das internationale Arbeiterparadies, die bedingungslos solidarische nationale Volksgemeinschaft, die allein das Weiterleben garantierende Klimarettung und so weiter. Die bürokratische Herrschaftsordnung dagegen ist der Weg, auf dem das große Ziel angeblich allein erreichbar ist.

Was dabei an rechtsstaatlicher Substanz unter die Räder kommt, wird als Kollateralschaden marginalisiert, wenn man die Ausschaltung einer freiheitlichen Ordnung nicht überhaupt zu einer vorübergehenden Erscheinung erklärt. In dem Letzteren waren die Marxisten groß. So sollte die Diktatur des Proletariats zum Sturz der überkommenen Ordnung zwar notwendig sein, der Staat nach Erreichung des angestrebten Fernziels aber irgendwann von selbst „absterben“, weil er nicht mehr gebraucht würde. Daran haben bis 1989 viele inbrünstig geglaubt, und zwar nicht nur unbedarfte Kretins, sondern auch renommierte Gesellschaftswissenschaftler.

George Orwell hat es beizeiten besser gewusst: „Die Macht ist kein Mittel“, schrieb er, „sie ist ein Endzweck. Eine Diktatur wird nicht eingesetzt, um eine Revolution zu sichern: sondern man macht eine Revolution, um eine Diktatur einzusetzen … Der Zweck der Macht ist die Macht.“ Und der Zweck der Zukunftsvision, könnte man fortfahren, ist es, eben dies zu kaschieren und der totalitären Vergesellschaftung aller menschlichen Beziehungen ein attraktives Mäntelchen umzuhängen. Was man dagegen unternehmen kann, hat Orwell leider nicht gesagt. Und so stehen wir denn vor dem offenbar unauflösbaren Widerspruch, dass die Wahrheit der für alle (außer den Bösen) offenen Gesellschaft die Diktatur ist, die Wahrheit der gegenüber allem (außer gegenüber Gedankenverbrechen) gepredigten Toleranz, die Zensur und die Wahrheit der Menschenliebe zu seinesgleichen und der unbändige Hass auf alle anderen.

Gewiss ist der Sozialismus auch eine Methode, angesichts einer überwältigenden Fülle von Partikularinteressen auch das „große Ganze“ der menschlichen Gesellschaft mitzubedenken und dem Individualismus nur auf sich selbst bezogener Egoisten das Recht der Menschheit als solcher entgegenzusetzen. Wenn Rudolf Bahro vor Jahren prognostizierte, das, was die verschiedenen Kräfte zusammenführen könne, werde „künftig kein besonderes Klasseninteresse, sondern langfristig-menschliches Interesse sein“, so wird ihm in dieser Allgemeinheit nicht leicht jemand widersprechen. Aber zu dem „Ganzen“, das es zu begreifen gilt, gehört auch die Wirkungsweise der sozialistischen Theorie selbst. Und diese ist bei der ganzen Diskussion unterbelichtet, um nicht zu sagen: unter einem Haufen ideologischen Mülls verborgen.

Zuerst erschienen bei der Achse des Guten. Mit freundlicher Genehmigung.

Johann Braun habilitierte sich für die Fächer Zivilprozessrecht, Bürgerliches Recht, Rechtsphilosophie und Privatrechtsgeschichte der Neuzeit und war von 1983 – 1988 ordentlicher Professor zunächst in Trier und von 1988 – 2011 in Passau.

Quellen:

Wolfgang Harich, Kommunismus ohne Wachstum? Sechs Interviews mit Freimut Duve und Briefen an ihn, 1975, 129.

Duve in: Harich (Fn. 1), 9.

Hans Jonas, Das Prinzip Verantwortung, 1979, 262.

Näher Johann Braun, MUT 44. Jg. (2013), Nr. 543, 10 – 17.

George Orwell, 1984, 3. Teil, 2. Kap.

Rudolf Bahro, Elemente einer neuen Politik. Zum Verhältnis von Ökologie und Sozialismus, 1980, 210.

Klima-Aktivisten hinterlassen Müll*

geschrieben von Klaus-eckart Puls | 22. Oktober 2019

Zur Kenntnis nehmen mussten die Berliner unter anderem, dass die Bewegung, die besonders laut vor „Klimanotstand“ und Artensterben warnen will, bei ihren Protestaktionen erstaunliche Müllberge hinterlassen hat. Allein nach der Protestaktion am Potsdamer Platz am 8. Oktober hat die Berliner Stadtreinigung (BSR) 11,5 Kubikmeter Müll eingesammelt. Nach Angaben eines BSR-Sprechers handelte es sich dabei „vor allem um Sperrmüll, zum Beispiel Matratzen und Stühle, sowie um Müllsäcke, die unter anderem mit Verpackungsabfällen gefüllt waren“. Zu den Hinterlassenschaften auf dem Potsdamer Platz gehörten sogar Zement und Badewannen. Nach einer Protestaktion von „Extinction Rebellion“ am Großen Stern im Berliner Tiergarten vielen abermals 8,5 Kubikmeter Müll an.

Anspruch und Realität klafften nicht allein in diesem Punkt weit auseinander: Erklärtermaßen will die radikale Gruppe so großen Druck auf die jeweiligen Regierungen ausüben, dass diese einen nationalen „Klimanotstand“ ausrufen. In Berlin hielten sich die Belastungen durch die Rebellionswoche für die Bundesregierung und die Politik allgemein jedoch in sehr überschaubaren Grenzen: „Extinction Rebellion“ hielt zwar im Regierungsviertel ein sogenanntes Klimacamp ab, auch gab es Proteste bei Parteizentralen, massivem Druck ausgesetzt waren aber überwiegend normale Bürger.

Seit dem 7. Oktober legten die Radikalen durch spontane Straßenblockaden immer wieder den Verkehr lahm, sodass es im Stadtgebiet immer wieder zu massiven Staus kam. Blockiert wurden mehrere verkehrswichtige Brü-cken in der Innenstadt. Aus Demonstrationen, die ordnungsgemäß angemeldet waren, starteten die Aktivisten immer wieder Blockaden von zentralen Verkehrsadern der Millionenstadt. Von solchen Aktionen waren der Kurfürstendamm, der Potsdamer Platz und der Große Stern betroffen.

Leidtragende waren dabei neben Autofahrern auch Fußgänger und Radfahrer. Sogar Nutzern des öffentlichen Nahverkehrs konnte es passieren, dass sie durch die rabiaten Blockadeaktionen der „Klimaschützer“ mit ihrem Bus im Stau steckenblieben.

Am Rande solcher Aktionen war immer wieder zu beobachten, wie insbesondere denjenigen, die aus beruflichen Gründen unterwegs waren, sprichwörtlich der Kragen platzte. Die spontanen Straßenblockaden in der Innenstadt stellten allerdings nicht nur die Geduld und Leidensfähigkeit vieler Berliner auf eine harte Probe. Strapaziert wurden auch das Gerechtigkeitsempfinden und das Vertrauen in den Rechtsstaat. Beobachter mussten abermals erleben, dass der Staat zwar Verstöße wie Falschparken konsequent ahndet, Blockaden des Straßenverkehrs, die Stunden und mitunter Tage andauerten, treffen allerdings bei Politikern des Berliner Senats auf erstaunlich viel Geduld und Nachsicht.

Berlins Innensenator Andreas Geisel (SPD) verteidigte gegenüber dem RBB das zurückhaltende Vorgehen der Beamten. Die Polizei schütze das Demonstrationsrecht und nicht den Inhalt von Versammlungen oder Demonstrationen. Dabei sei man gut beraten, mit professioneller Gelassenheit und Augenmaß zu handeln und die Situatuion nicht eskalieren lassen.

Sehr scharfe Kritik äußerte dagegen Marcel Luthe (FDP). Der Berliner Innenpolitiker sagte mit Blick auf die Straßenblockaden: „Wer statt mit Argumenten und durch Wahlen und Abstimmungen für seine Positionen zu werben, lieber anderen durch Einschränkung ihrer Freiheitsrechte seinen Willen aufzwingt, stellt sich außerhalb des demokratischen Konsenses.“ Tatsächlich könnten die rücksichtslosen Aktionen von Aktivisten der „Extinction Rebellion“-Bewegung dafür gesorgt haben, dass bei betroffenen Berlinern so manche bislang gehegte Illusion über die „Klimaschützer“ verflogen ist.

Auch die begleitende Berichterstattung zur Rebellionswoche wirkte teilweise wie ein Augenöffner: Hingewiesen wurde etwa auf die kaum zu übersehenden antidemokratischen Seiten der Bewegung. In einem „Spiegel“-Interview aus dem September hatte beispielsweise der Brite Roger Hallam, einer der Gründer von „Extinction Rebellion“, geäußert: „Wenn eine Gesellschaft so unmoralisch handelt, wird Demokratie irrelevant.“ Das heißt nichts anderes als: Wenn wir unsere Ziele nicht demokratisch erreichen, dann muss die Demokratie weg.

In der „Neuen Zürcher Zeitung“ sprach sich Annemarie Botzki, eine der deutschen Sprecherinnen von „Extinction Rebellion“, zudem für die Schaffung von „Bürgerinnenversammlungen“ aus. „Wir wollen die Demokratie erweitern“, so die Botzki. Kritiker wenden ein, diese vermeintliche „Erweiterung“ laufe in Wahrheit auf eine Kontrolle und Entmachtung der demokratisch gewählten Parlamente unter dem Vorwand des angeblichen „Klimanotstands“ hinaus.

=================================================================

)* Anmerkung der EIKE-Redaktion :

https://www.preussische-allgemeine.de/

=================================================================

Schadet uns Kohlenstoffdioxid?

geschrieben von Chris Frey | 22. Oktober 2019

Physikalische Grundlagen

₂soll zu Klimaerwärmung und Umweltkatastrophen führen. Stimmt diese Behauptung? Physiker kennen das Henry-Gesetz: Bei stärkerem Druck und bei niedrigerer Temperatur löst sich mehr Gas in einer Flüssigkeit. Wir können das beobachten, wenn wir kalte und warme Flaschen mit Mineralwasser öffnen. Die warme sprudelt viel stärker als die gekühlte. Ist die Luft kälter, löst sich mehr CO₂ aus der Luft in Seen, Flüssen, Regenwolken und im Meer. Weil Wasser viel mehr CO₂als Sauerstoff und Stickstoff aufnimmt¹, sinkt dabei der CO₂-Anteil in der Luft. Tiefenbohrungen im Meer und im Eis an den Polen haben bestätigt, dass das CO₂ der Luft dem Klima mit einer Zeitverzögerung folgt. Ein Ansteigen des CO₂-Anteils der Luft ist eine Folge der Klimaerwärmung und kommt daher als Ursache der Klimaerwärmung wohl nicht in Frage.

⁴

Temperaturverlauf seit Entstehung der Erde. Quelle: ZAMG

Das Klima wandelt sich seit seiner Entstehung

Klima beschreibt den typischen Zustand der Atmosphäre über lange Zeiträume von Jahren bis zu Jahrmillionen im Wechselspiel mit Gewässern, Landmassen, Eisflächen und Lebewesen.⁵ Nach heutigem Stand der Wissenschaft entstand unsere Erde vor 4,6 Milliarden Jahren zusammen mit der Sonne und den übrigen Planeten aus einem Urnebel. Sie kühlte zuerst rasch, dann immer langsamer ab. Dabei bildeten sich zuerst eine feste Kruste und später Ozeane. Vor 2,5 Milliarden Jahren war das heutige Temperaturniveau erreicht. Vor 2,2 Milliarden Jahren und nochmals vor 700 Millionen Jahren war die Erde ein gefrorener Schneeball. Die allermeiste Zeit ihrer Geschichte wie auch der letzten 542 Millionen Jahre, in denen Leben nachgewiesen werden kann (Phanerozoikum), war die Erde eisfrei. Ihr Klima war also wärmer als heute.⁶ Vor 5 Millionen Jahren pendelte das Klima hauptsächlich in den 23.000 bis 41.000-jährigen Zyklen der Schiefe und der Präzession der Erdachse, danach nahmen die Schwankungen weiter zu. Seit 900.000 Jahren dominiert der 100.000 Jahreszyklus der Exzentrizität der Erdbahn. Vor 2,6 Millionen Jahren vereiste die Antarktis. In der Arktis fror das Meer im Winter. Das fünfte Eiszeitalter, in dem wir leben, begann. Seit einer Million Jahren lösen sich Kalt- und kürzere Warmzeiten ab. Die Mitteltemperatur des Erdglobus schwankt um 5°C. Die letzte Kaltzeit unseres Eiszeitalters war vor 110.000 bis 12.000 Jahren. In ihr wechselte das Klima 24 Mal abrupt zwischen wärmeren und kälteren Perioden. Am kältesten war es vor 25.000 bis 20.000 Jahren. Damals waren Nordamerika, Grönland und weite Teile Europas und Asien von Eis bedeckt. Salzburg war unter 600 m, Rauris unter 1,5 km Eis begraben. Nur die höchsten Berge der Alpen waren eisfrei. Der Meeresspiegel sank weltweit um 120 m. Dadurch waren Meere wie die Adria verschwunden, Alaska war mit Sibirien und Britannien mit Europa verbunden. Der Kälteeinbruch muss plötzlich gekommen sein. In den Mägen von Mammuts, die das Eis in Sibirien freigibt, finden wir noch heute die Nahrung.⁷ Vor 11.700 Jahren begann die heutige Warmzeit, das Holozän. Der Großteil des Holozäns war etwas wärmer als das 20. Jahrhundert. In der warmen Periode Atlantikum vor 6.000 Jahren grünte die Sahara. Seit 5.000 Jahren kühlt das Klima langsam ab. Zwischen 300 vor Christus und 400 nach Christus erwärmte sich das Klima wieder (römisches Klimaoptimum). Mäßig kühlem Klima während der Zeit der Völkerwanderung folgte das mittelalterliche Klimaoptimum zwischen 950 und 1250. In Britannien wurde Wein anbaut. In Europa blühten Städte und Staaten auf, die Bevölkerung wuchs.⁸ 984 wurde der Wikinger Erich der Rote nach Grönland verbannt, das er das „grüne Land“ nannte. Er überzeugte 700 Landsleute, nach Grönland auszuwandern. Damals war die Durchschnittstemperatur höher als heute.⁹ Davon zeugen in Permafrost eingefrorene Wikinger-Gräber. Vom 15. bis 19. Jahrhundert hatten wir die Kleine Eiszeit. Missernten und Seuchen der frühen Neuzeit verschärften bestehende soziale Spannungen. Hexenverfolgung und französische Revolution sind in diesem Licht zu sehen. Die Alpengletscher erreichten um 1850 ihre größte Ausdehnung seit 6.300 Jahren. Danach erwärmte sich das Klima wieder.

Temperaturverlauf des Holozäns. Quelle: ZAMG

2. Dabei können sich diese winzigen Algen¹² unbegrenzt vermehren. Sie haben Kalkgebirge aufgebaut. Nicht nur die Steinbildung, sondern auch Chitinpanzer von Insekten und Pilzen binden CO₂. Heutzutage ist nur mehr so wenig CO₂ in der Atmosphäre, dass viele Gärtner CO₂ in ihre Gewächshäuser einbringen, damit die Pflanzen besser wachsen. In spätestens einer halben Million Jahren wird so wenig CO₂ in der Luft sein, dass die Pflanzen die Photosynthese nicht mehr ausführen und keine höheren Wirbeltiere und schon gar keine Menschen auf der Erde leben können.

CO₂ und Temperatur der Luft in der Antarktis. Quelle: ZAMG

Der Arktische Ozean ist bis zu 5.669 m tief. In ihm schwimmen die Eismassen des Nordpols. Selbst wenn sie schmölzen, würde der Meeresspiegel dadurch nicht dramatisch ansteigen. Jeder von uns kann das mit einem Eimer voller Eiswürfel beobachten. Er wird bis zum Rand mit Wasser gefüllt. Das Eis schwimmt an der Oberfläche. In der Wärme schmilzt es ohne dass auch nur ein Tropfen Wasser überläuft (Archimedisches Prinzip). Die Antarktis zählt dagegen zu den kältesten Gebieten der Erde. Auf dem Nordpol hat es im Winter konstant -65°C. Im Midsommer steigt die Temperatur auf -25°C.¹³ Eine Angst vor dem Schmelzen des Eises der Pole ist vollkommen unbegründet.

Sonne, Erde und Sterne schaffen das Klima

Obliquität dauert 41.000 Jahre. Sonnenflecken treten in einem 11 jährigen Zyklus auf, der zwischen 9 und 14 Jahren variieren kann. Sie sind immer paarweise, wobei ein Sonnenfleck in die Sonne, der andere aus der Sonne heraus reicht. Im nächsten Zyklus sind die Polaritäten vertauscht. Daher sprechen wir auch von einem 22 jährigen Zyklus. Weitere Sonnenzyklen mit einer Dauer von 88 (Gleissberg-Zyklus), 208 (Suess/de Vries-Zyklus), 500, 1.000 (Eddy-Zyklus) und 2.300 Jahren (Hallstatt-Zyklus) wurden beobachtet.¹⁴

Der Gleichklang zwischen Sonnenaktivität und mittlerer Erdtemperatur ist inzwischen lückenlos gesichert. Am wahrscheinlichsten erscheint die 1997 von den dänischen Forschern Eigil Friis-Christensen, Knud Lassen und Henrik Svensmark vorgeschlagene Hypothese der Wolkenbildung durch kosmische Strahlung, die vom Magnetfeld der Sonne abgeschwächt wird. Die Forscher Nicola Scafetta und Bruce J. West wandten dazu neuartige statistische Verfahren an und bestätigten die Gültigkeit dieses Gleichklangs auch für die wenigen Zeitabschnitte, in denen die mathematische Korrelation keine guten Ergebnisse ausweist.¹⁵

Der slowakische Klimaforscher Jan Veizer und der israelische Astrophysiker Nir J. Shaviv beschrieben einen komplexen Zusammenhang. Die kosmische Strahlung nimmt zu, wenn unser Sonnensystem alle 143 Millionen Jahre einen der vier Spiralarme unserer Milchstraße durchquert. Dieser Rhythmus stimmt mit den Eiszeiten überein. Mehr Sonnenflecken gehen mit einem erhöhten Magnetfeld der Sonne einher. Dieses verringert die kosmische Strahlung in der Erd-Atmosphäre. Die Strahlung erzeugt Keime, die zur Kondensation und Wolkenbildung führen. Wolken schirmen die Erde von der Sonne ab. Daher ist es auf der Erde kühler, wenn die Sonnenflecken abnehmen. Dieser Zusammenhang wird von Satellitenbeobachtungen der letzten Jahre bestätigt. Veizer und Shaviv fanden diesen kosmischen Ursprung von Klimaänderungen in der Strahlung von 50 verschiedenen Eisenmeteoriten bestätigt.¹⁶

Das Maunder-Minimum war die kühlste Periode der Kleinen Eiszeit am Ende des 17. Jahrhunderts. Damals wurden so gut wie keine Sonnenflecken beobachtet. Wie der Geologe Roger Higgs erforschte, folgt das Klima mit einer Verzögerung von 25 Jahren dem Magnetfeld der Sonne. Das Magnetfeld der Sonne hatte 1991 einen Höhepunkt. Das stimmt mit der Temperaturspitze 2016 überein. Mittlerweile sind die Sonnenflecken in dramatischer Abweichung von ihren bisherigen Zyklen verschwunden. Das Klima wird daher zumindest bis 2044 kühler.¹⁷ Bereits 1972 haben Klimaforscher vor einer bevorstehenden Kaltzeit gewarnt.¹⁸

Der Weltklimarat

Der Weltklimarat IPCC wurde 1988 von der UNO gegründet, um Ausmaß und Auswirkungen des Klimawandels aufzuzeigen und Gegenmaßnahmen anzuregen. Treibende Kraft war der sozialistische kanadische Milliardär Maurice Strong (1929-2015), der in dem Thema einen Hebel sah, die UNO zu einer Weltregierung auszubauen.¹⁹ Seine Cousine, die US Journalistin Anna-Louise Strong, unterstützte seit 1921 den Aufbau des Kommunismus in Russland propagandistisch. Nachdem sie Stalin 1949 als Spionin verhaften ließ, wanderte sie nach China aus wo sie die Freundschaft mit Mao Zedong und Zhu Enlai erlangte.²⁰ Strong selbst war mit vielen führenden Persönlichkeiten wie Justin Trudeau, Richard Nixon, den Rockefellers, Prinz Philip von Edinburgh, Saddam Hussein, George Soros und Mao Zedong gut vernetzt.²¹ Der Weltklimarat befasst sich entsprechend seinem Auftrag so gut wie ausschließlich mit dem menschengemachten Klimawandel. Dabei beruft er sich auf das längst widerlegte Hockeyschläger-Diagramm aus dem Jahr 1999.²² Die natürlichen Schwankungen des Klimas werden weitgehend ausgeblendet. Mittlerweile haben die meisten einschlägigen Naturwissenschaftler den Weltklimarat verlassen. Soziologen, Ökonomen und Politologen geben den Ton an.

Al Gore war von 1993 bis 2001 Vizepräsident der Vereinigten Staaten. Seine Vorträge über einen durch Treibhausgase ausgelösten Klimawandel fasste er 2006 im Film „Eine unbequeme Wahrheit“ (An Inconvenient Truth) zusammen. Wegen einiger Fehler und Übertreibungen darf dieser Film in britischen Schulen nicht ohne Richtigstellungen gezeigt werden. 2007 erhielt Al Gore für ihn den Oscar für den besten Dokumentarfilm und zusammen mit dem Weltklimarat IPCC den Friedensnobelpreis. Gore‘s Investmentfonds Generation Investment Management GIM besaß 10 % der Chicago Climate Exchange, der amerikanischen Terminbörse für den Handel mit Emissionsrechten und diese die Hälfte der European Climate Exchange.²³ Vor 2010 konnte Al Gore seinen Privatbesitz hauptsächlich mit Umweltgeschäften auf 100 Millionen Dollar verfünfzigfachen.²⁴ Im Kyoto-Protokoll verpflichteten sich 1997 einige Industriestaaten, den Ausstoß ihrer Treibhausgase zu reduzieren. Die USA haben das Protokoll zwar unterzeichnet, aber nicht ratifiziert. Auch als Al Gore Vizepräsident war, wurde es dem Senat nie zur Abstimmung vorgelegt.²⁵

97 % des CO₂, das in die Atmosphäre gelangt, ist natürlichen Ursprungs: Vulkane, Atemluft, Vegetation, Gewässer²⁶. Nur 3 % setzen Menschen durch das Verbrennen fossiler Energien frei. Davon stammen 27,5 % von der Volksrepublik China, 16,9 % von den USA, 5,9% von Indien und 4,7 % von Russland.²⁷ Keines dieser Länder hat sich verpflichtet, den CO₂ Eintrag zu verringern. Der Beitrag von Deutschland ist mit 2,2 % zu vernachlässigen. Selbst wenn Deutschland keinen Tropfen Öl mehr verbrannte, wäre das für den CO₂-Gehalt der Erdatmosphäre belanglos.

1896 berechnete der Schwedische Nobelpreisträger für Chemie Svante Arrhenius, dass eine Verdoppelung des CO₂-Gehalts der Atmosphäre durch einen Treibhauseffekt zu einer Temperaturerhöhung um 4 bis 6°C führt. Er erwartete dies in 3.000 Jahren und freute sich dabei auf gleichmäßigere und bessere klimatische Verhältnisse und um das Vielfache erhöhte Ernten.²⁸ Bis heute ist der Treibhauseffekt experimentell nicht nachgewiesen.

Die Grenzen der Klimamodellierung

Im SPIEGEL 13/2019 plaudern zwei führende Klimaforscher aus dem Nähkästchen. Bjorn Stevens vom Hamburger Max-Planck-Institut für Meteorologie forscht seit mehr als 20 Jahren auf dem Feld der Klimamodellierung. In den 1979er Jahren vermuteten Forscher, dass eine Verdoppelung des CO₂ Gehalts der Atmosphäre zu einer Temperaturerhöhung um 1,5 bis 4,5°C führen könnte. Diese Klimasensitivität legten sie ihren Computer-Simulationen zu Grunde. Die Rechenleistung der Computer ist auf das Vielmillionenfache gestiegen, aber die Vorhersage der globalen Erwärmung ist so unpräzise wie eh und je. Das empfindet Stevens als zutiefst frustrierend. „Unsere Computer sagen nicht einmal mit Sicherheit voraus, ob die Gletscher in den Alpen zu- oder abnehmen werden.“ Kondensiertes Wasser – also Wolken haben den größten Einfluss auf das Klima. Mal bilden sie zarte Streifen, mal treiben sie in Herden bauschiger Gebilde dahin, mal bäumen sie sich zu kilometerhohen Unwetterfronten auf. Manche bestehen aus winzigen Wassertröpfchen, andere aus kleinen Körnchen aus Eis. Schiebt sich eine Wolke vor die Sonne, wird es kühler. In der Nacht und im Winter verhindern Wolken, dass Wärme abgestrahlt wird. Alle Wolken zusammen würden zu Wasser kondensiert unseren Globus mit einer 0,1 mm dünnen Schicht bedecken. Durch eine Verringerung der tief hängenden Gewitterwolken (Cumulonimbus) um 4 % würde es weltweit um 2° C wärmer. (2015 wurde auf der Pariser Klimakonferenz beschlossen, die Erwärmung der Erde auf diese 2° C zu begrenzen.) Die Bildung von Wolken ist stark von kleinräumigen Wirbeln abhängig, die nach wie vor nicht erfasst, geschweige denn prognostiziert werden können. Wie vor 50 Jahren modellieren die Forscher die Erde möglichst exakt und geben vor, wie stark die Sonne in welcher Weltregion strahlt. Daraus simuliert der Computer Temperaturen. Wasser kann dabei nicht verdunsten, aufsteigen und kondensieren. So lässt sich nur die Großwetterlage abbilden. Tiefdruckwirbel ziehen wie in der Wirklichkeit über den Nordatlantik. Indien wird im Sommer vom regenreichen Monsun heimgesucht. In verschiedenen Klimamodellen klaffen die Temperaturen der Arktis um 10°C auseinander. Das lässt jede Prognose der Eisbedeckung als Kaffeesatzleserei erscheinen. „Wir brauchen eine neue Strategie“, sagt Stevens.

„Auch fehlen wichtige Daten wie die Feuchtigkeit und die Strömungen innerhalb der Wolken. Schneider hat berechnet, dass sich die Stratokumuli über den subtropischen Ozeanen großflächig auflösen könnten, falls der CO₂ Gehalt der Luft auf 0,1 % ansteigt. Das ist mehr als das Dreifache von heute und wird selbst in den düstersten Treibhausszenarien nicht erreicht. In diesem Modell verflüchtigte sich die Wolkendecke über Pazifik und Atlantik. Dabei stieg die Welttemperatur zu seiner Überraschung nur um 8°C. „Es scheint dort eine Nichtlinearität zu geben, die wir bisher nicht kannten“, sagt er. „Das zeigt, wie schlecht die Stratokumuli bisher verstanden sind.“ „Denkbar ist aber auch, dass es prinzipiell unvorhersehbare Klimaphänomene gibt“, sagt Stevens. „Dann können wir noch so genau simulieren und kommen trotzdem zu keinen verlässlichen Ergebnissen.“ Dann steuert die Menschheit auch weiterhin ins Ungewisse.²⁹

Wer finanziert die Klimapanik?

Westliche Politiker wollen Arbeitsplätze schaffen und zukunftsweisende Entscheidungen treffen. Zur Unterstützung holen sie Berater, die oft Interessen der Großindustrie vertreten. Die repräsentative Demokratie führt zu plakativen Slogans ohne Nuancierungen. Sachzwänge, Zeitdruck und die Interessen Einzelner bewirken, dass Neues eingeführt wird, bevor Vor- und Nachteile untersucht sind.

Institute, die Teilaspekte der Klimaerwärmung untersuchen, erhalten schier unbeschränkte Forschungsgelder, wenn ihre Studien die These eines menschengemachten Klimawandels stützen. So liefern enthusiastische Studenten und Lehrende trotz ihrer Bemühungen um Logik, Ehrlichkeit und Objektivität oft Mosaiksteinchen für ein Bild aus Dogmen und Lügen.

Wollen Milliardäre wie Bill Gates, Mark Zuckerberg, Jeff Bezos, Richard Branson³⁰ und George Soros³¹ mit dem Schüren einer Klimahysterie Macht und Reichtum vermehren, die Menschheit und unser Leben umkrempeln oder vielleicht sogar die Zahl der Menschen auf der Erde drastisch verringern?

Für die Staaten der Europäischen Union wurden Emissionszertifikate für 2 Milliarden Tonnen CO₂ ausgegeben³². Bei einem derzeitigen Kurs von 28 €³³ haben diese Zertifikate einen Börsenwert von 56 Milliarden €. Sie belasten damit jeden der 513 Millionen EU-Bürger³⁴ mit durchschnittlich 109 €. Dazu kommen unter anderem Strafzahlungen für nicht erreichte Klimaziele, der Aufwand für jährliche Klimakonferenzen seit dem Berliner Klimagipfel 1995³⁵ sowie Kosten für Verwaltung, Werbung, Forschung, Massenmedien und Demonstrationen. Das Denken und die Gefühle von Millionen von Menschen werden von wesentlichen Themen abgelenkt.

Neben den Nutznießern der CO₂-Emissionszertifikate³⁶ und ihres Handels gibt es eine Reihe von Branchen mit schier unerschöpflichem Werbebudget, die riesige Profite aus der Hysterie um eine menschengemachte Klimaerwärmung ziehen. Versicherungen können ihre Prämien erhöhen, wenn der Klimawandel vermehrte und verheerendere Unwetter als in der Vergangenheit erwarten lässt. Die Erdölindustrie hat in „grüne Energien“ investiert, für deren Herstellung immense fossile Energien verwendet werden.³⁷ Überdies möchte sie über eine längere Zeit weniger Öl teurer verkaufen.

³⁸

³⁹ für Elektroautos.

PR-Agenturen haben die Gefühle vieler Menschen aufgewühlt und sie überzeugt, dass nur ein sofortiger großer Kraftakt den Untergang unseres Planeten gerade noch verhindern könnte. Daher ordnen alle staatstragenden Parteien und Medien ihre Aussagen, Artikel, Filme und Gesetze diesem Ziel unter. In Krisenzeiten nähern sich die Ziele und Parolen der verschiedenen Parteien noch weiter aneinander an. Wer selber denkt oder Pluralismus fordert, wird als „Klimaleugner“ der Lächerlichkeit preisgegeben. Welcher Politiker kann der Versuchung widerstehen, ohne Gefahr einer Abwahl das Zusammenleben seiner Bürger bis ins kleinste Detail zu regeln? 2016 beschloss die deutsche Bundesregierung den Klimaschutzplan 2050. Rechtzeitig davor werden keine mit Benzin oder Diesel betriebenen Neuwagen zugelassen.

Das Heizen mit Kohle, Öl oder Erdgas wird verboten. Dabei ist genauso wenig wie die Endlagerung der radioaktiven Abfälle von Atomkraftwerken geklärt, welche Technologien Kohle, Erdöl und Erdgas ersetzen sollen. Nicht überall können oder dürfen Wasserkraftwerke gebaut werden. Ohne Förderung sind weder Windparks noch Photovoltaikanlagen oder Hackschnitzelkraftwerke wirtschaftlich. Transport und Speicherung des erzeugten Stroms sind nicht gelöst. Zur Versorgungssicherheit sind konventionelle Kraftwerke mit fast der gleichen Leistung notwendig.⁴⁰ Windräder sind laut, verschandeln die Landschaft und töten Fledermäuse und Vögel. Große Raubvögel wie der Weißkopfseeadler – das Wappentier der USA – brüten nicht jedes Jahr und haben nur ein Junges. Windkraftwerke drohen, sie auszurotten. In Österreich wurden geförderte Biogasanlagen mittlerweile stillgelegt.⁴¹ Wir könnten mehr Autos mit Erdgas antreiben. Das wird hintertrieben, um eine engere Beziehung zwischen Europa und Russland zu verhindern. Weil Methan als 25-mal so schädliches Treibhausgas wie CO₂gilt, können sich die Staaten im nächsten Schritt einigen, die Haltung von Rindern, Ziegen und Schafen und den Fleischkonsum zu reglementieren. So wird die Freiheit jedes einzelnen Menschen Schritt für Schritt beseitigt.

Das größte Interesse an der Klimahysterie haben jedoch die Militärs. 2018 wurden weltweit 1.822 Milliarden US Dollar für Militärs ausgegeben. Das sind 239 US Dollar pro Mensch. 36 % davon tätigten die USA, 14 % China, 3,7 % Saudi-Arabien und Indien, 3,5 % Frankreich, 3,4 % Russland, 2,7 % Großbritannien und Deutschland.⁴²

Zumindest die USA, Russland, China und Kanada arbeiten an Geoengineering als Waffe. Ein Memorandum der CIA vom 22.11.1960 erklärt: „Die Klimakontrolle in großem Maßstab erfordert die Veränderung der globalen Wettermuster durch Veränderung und Beeinflussung der physikalischen Prozesse in großem Maßstab, die verbunden sind mit den charakteristischen Bewegungen der allgemeinen atmosphärischen Zirkulationen im großen Maßstab.“ Die Ionosphäre muss kontrolliert werden, weil sie unberechenbar ist. Geologen haben das Klima zu simulieren und ihre Beeinflussung zu testen.⁴³

Die USA entwickelten den Hochfrequenzapparat zur Energieübertragung von Nikolai Tesla weiter. Entsprechende Patente beinhalten die Erhitzung der Erdatmosphäre. Mit HAARP (High Frequency Active Auroral Research Program) Anlagen bei Gakona in der Wildnis Alaskas und Marlow bei Rostock in Mecklenburg-Vorpommern wird ein Spiegel über der Atmosphäre errichtet, mit dem die Kommunikation mit U-Booten möglich ist, die Erdatmosphäre erhitzt und das Wetter verändert werden kann. Ziel ist nicht nur die Veränderung des Klimas sondern die Kontrolle über das Bewusstsein der Menschen.⁴⁴

Die westliche Demokratie erfordert, dass gravierende Eingriffe in das Leben der Menschen von einer Mehrheit zumindest toleriert werden. Das Dogma vom menschengemachten Klimawandel gipfelt in einem Ruf nach Eingriffen in die Klimahülle der Erde, dem der militärisch-industrielle Komplex gerne folgt. Die dazu notwendigen Technologien hat er in den letzten Jahrzehnten entwickelt und getestet.⁴⁵

Es ist erschreckend, welche Auswirkung der Einfluss von Wirtschaft und Staat auf die Lehrinhalte von Kindergärten, Schulen und Universitäten hat. Er lässt im Bewusstsein einer Mehrheit der Menschen Propaganda, Unwahrheiten und Lügen als ein Wissen erscheinen, dem 97 % aller Wissenschaftler zustimmen. Es wäre an der Zeit, Schulen und Universitäten die Lehrfreiheit zu gewähren bzw. zurück zu geben.

CO₂ könnte mithelfen, den Ausbruch der nächsten Kaltzeit erträglicher zu machen und die Zahl ihrer Todesopfer zu verkleinern. Milliarden Menschen wohnen in Städten und wünschen sich schönes, warmes, trockenes Wetter. Wünsche gehen öfter in Erfüllung als uns bewusst ist. Sind sie nicht zu Ende gedacht, haben sie oft unliebsame Auswirkungen. Nach Rudolf Steiner, dem Gründer der Anthroposophie beeinflussen wir mit allen unseren geistvollen und materialistischen Gedanken die Sonnenflecken und damit unser Klima.⁴⁶

Für mehr Umweltschutz

Auch wenn wir wissen, dass fossile Brennstoffe keine bedrohliche Klimaänderung hervorrufen, haben wir keinen Grund, uns entspannt zurück zu lehnen. Um unsere Umwelt lebenswert zu erhalten, brauchen wir einen konsequenten Umweltschutz, der viel tiefer geht als sich die meisten von uns vorstellen können. Voraussetzung ist, dass jeder Einzelne sich um Wahrheit bemüht und versucht, stets den gleichen Maßstab anzuwenden. Wir sollten uns angewöhnen, vor Beginn jeder Produktion und umso mehr vor Einführung einer neuen Technologie den gesamten Prozess vom Beginn der Planung über die Gewinnung und Herstellung der benötigten Rohstoffe, die Produktion und die Nutzung bis zur Entsorgung zu ermitteln und abzuwägen. Ein ganzheitliches Denken beinhaltet, dass wir uns und die Erde auch als geistige Wesen betrachten.

Extreme Ansichten bedingen einander. Vielen Bewohnern der USA ist nur der materielle Teil der Wirklichkeit bewusst. Anderseits dürfen in manchen Gegenden der USA Schulen und Museen nicht behaupten, dass vor 100 Millionen Jahren Saurier auf der Erde gelebt haben. Schließlich kann man aus der Bibel ausrechnen, dass Gott die Erde im Jahr 3761 vor Christus geschaffen hat. In der Volksrepublik China werden alle Menschen sowohl im realen Leben als auch digital streng überwacht. In einem „Sozialkreditsystem“ sollen alle Bürger bewertet und bei Abweichen von staatlichen Vorgaben bestraft werden.⁴⁷ Trotzdem kennt der Staat die Anzahl seiner Bürger nicht einmal auf 100 Millionen Menschen genau, weil durch die Ein-Kind-Politik von 1979 bis 2015⁴⁸ viele Menschen als U-Boot leben.

In unserem Wirtschaftssystem kann jedes Unternehmen das produzieren, was der Vorstand will und danach versuchen, die Produkte mit Werbekampanien an den Konsumenten zu bringen. Das ist eine große Vergeudung von Rohstoffen, Geld und Arbeit.

Die Zinseszinsrechnung zeigt, dass ein ständiges Wachstum nicht möglich ist. Hätte Josef zu Christi Geburt einen Cent mit 3,7 % Verzinsung angelegt, könnte heute mit dem Guthaben die ganze Erdkugel aus purem Gold bezahlt werden.⁴⁹

Rücksichtslos wird mit Dünger, Gentechnik und Pflanzenschutzmitteln möglichst viel Ernte aus dem Boden heraus gepresst. Um den Preis zu stützen, wird ein erheblicher Teil der Ernte vernichtet. Viele Supermarktketten vernichten unverkaufte Lebensmittel auch wenn sie noch einwandfrei sind. Kühe werden ihr Leben lang in Ställen gehalten, obwohl saftige Weiden davor liegen. Kälber werden systematisch von ihren Müttern getrennt und mit Milchersatz gefüttert⁵⁰, obwohl mehr Milch produziert als verkauft wird. Mit der Enthornung schaden wir nicht nur den Rindern sonder mindern auch die Qualität der Milch und des Fleisches.⁵¹^,⁵² Durch die Homogenisierung der Milch gelangen zerkleinerte Fettpartikel zu früh ins Blut.⁵³

Monokulturen, Hybridpflanzen und Patente auf Pflanzen nützen nur großen Chemie- und Agrarkonzernen. Sie richten sich gegen die Natur. In exakt in Reih und Glied gepflanzten Fichtenwäldern wachsen durch Samenanflug fast nur Laubbäume. Wir Menschen schneiden sie um und wundern uns, dass sich Borkenkäfer ausbreiten. Bei einer Vierfelder-Wirtschaft kann sich der Maiszünsler nicht bedrohlich vermehren. Das Abholzen von tropischen Regenwäldern sollte ähnlich wie Wilderei als Verbrechen gegen die Menschheit und die Erde geahndet werden.

Durch moderne Fischerei töten wir viele junge Fische und Tiere, die wir nicht essen wie Delphine und Pinguine. Die Leiter der Fischereiflotten wissen, dass ein nachhaltiger Fischfang ihren Fang vergrößern würde. Trotzdem machen sie weiter wie bisher, damit die Konkurrenz keinen Vorteil aus ihrer Nachhaltigkeit ziehen kann. Auch beim Umweltschutz kommt es auf ein gesundes Augenmaß an. Nicht die an den Küsten lebenden Fischer haben die Meere leergefischt, sondern die großen Trawler. So sollten die Inuit wie in den Jahrhunderten davor Robben jagen dürfen.

Naturgemäß können hier nur einige Themen angeschnitten werden. Viele Fragen bleiben offen wie:

Verhungern in der dritten Welt Menschen, weil wir mit Biosprit unser Gewissen beruhigen?

Wie werden wir die Berge aus weder verwertetem noch entsorgtem Plastik los?

Schadet uns Elektrosmog? Wie sehr schaden die verschiedenen Mobilfunknetze unserer Gesundheit? Bekommen wir ein 5G Netz, um noch schneller Musik und Filme herunter landen zu können? Oder weil Militärs es wollen?

Wie gefährlich sind Mikrowellen?

Wie viel Energie, Ressourcen und Lebenskräfte verbrauchen unsere Computer? Wie viel die Suchmaschinen wie Google und DuckDuckGo oder das Schürfen von Crypto-Währungen?

Führen wir in Europa Elektrofahrzeuge ein, weil die Volksrepublik China mit dieser Maßnahme den Smog bekämpft?

Walter Michael Hopferwieser

Stand: 13.10.2019

1 https://www.unternehmensberatung-babel.de/industriegase-lexikon/industriegase-lexikon-n-bis-z/ostwald-koeffizient/gase-geloest-in-wasser.html

2 https://www.ris.bka.gv.at/Dokumente/BgblAuth/BGBLA_2007_II_243/COO_2026_100_2_366060.pdfsig

3 https://de.wikipedia.org/wiki/Kohlenstoffdioxid

4 https://www.scinexx.de/news/geowissen/erdatmosphaere-reicht-bis-zum-mond/, abgerufen am 15.07.2019

5 https://www.zamg.ac.at/cms/de/klima

6 https://www.zamg.ac.at/cms/de/klima/informationsportal-klimawandel/klimavergangenheit/palaeoklima/4-6-mrd.-jahre

7 Axel Burkart Klimaschwandel 2

8 https://www.zamg.ac.at/cms/de/klima/informationsportal-klimawandel/klimavergangenheit/palaeoklima/2.000-jahre

9 https://akademie-zukunft-mensch.com/wp-content/uploads/Klimaschwandel.pdf, Seite 38 von 52