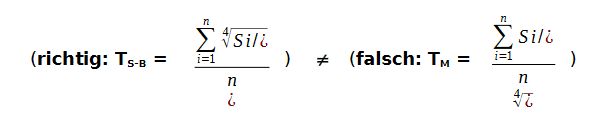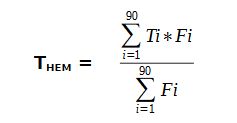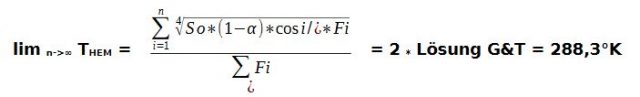Anmer­kungen zur hemisphä­rischen Mittelwert­bildung mit dem Stefan-Boltzmann-Gesetz

Der vorläufigen IPCC-Inquisition ist in ihrer Kritik meines hemisphärischen S-B-Ansatzes weiterhin eine rein „astrophysikalische“ Sicht auf unsere Erde vorzuwerfen. Ausgerechnet jener Anblick aus dem All, der das optische Bild unseres „Blauen Planeten“ prägt, ist nämlich derjenige Anteil der solaren Einstrahlung, der gar nicht an der globalen Temperaturgenese auf der Tagseite unserer Erde beteiligt ist. Und der ominöse „Faktor 4“ der vorläufigen IPCC-Inquisition beschreibt dann sofort eine Art globaler Abstrahlung.

Nun liegt die „Temperaturwerdung“ (Temperaturgenese) auf der Tagseite unserer Erde (@2πR²) aber genau zwischen solarer Einstrahlung (@πR²) und terrestrischer Abstrahlung (@4πR²) – denn kein vernünftiger Mensch dürfte abstreiten, dass es auf unserer Erde Tag und Nacht gibt. Es gilt auf unserer Erde also für das rechnerische S-B-Temperaturäquivalent (S-B-T):

(S-B-T Einstrahlung @ πR²)≠(S-B-T Tagseite @ 2πR²) ≠ (S-B-T Abstrahlung @ 4πR²)

Um den ominösen „Faktor 4“ der vorläufigen IPCC-Inquisition für die Temperaturgenese auf unserer Erde vermittels eines vorgeblich „natürlichen atmosphärischen Treibhauseffektes“ zu erschüttern, mag ein Verständnis der Entwicklungsgeschichte meines hemisphärischen Stefan-Boltzmann-Ansatzes hilfreich sein. Ich erlaube ich mir daher, alle meine Beiträge zum hemisphärischen S-B-Ansatz hier auf EIKE unter (*) in der Schlussbemerkung noch einmal komplett aufzulisten.

Mit keinem anderen physikalischen Gesetz wird so viel Schindluder getrieben wie mit dem Stefan-Boltzmann-Gesetz. Das Stefan-Boltzmann-Gesetz stellt eine Beziehung zwischen Temperatur und Strahlungsleistung eines Schwarzen Körpers in einem GLEICHZEITIGEN gemeinsamen thermischen Gleichgewicht her. Dieses physikalische Gesetz wird aber häufig dazu missbraucht, um beliebig ermittelte Durchschnittswerte der Strahlungsleistung in eine Temperatur oder umgekehrt beliebig ermittelte Durchschnittstemperaturen in eine Strahlungsleistung umzurechnen, die weder zeitgleich eintreten noch physikalisch direkt miteinander interagieren.

Die allgemeine Form des Stefan-Boltzmann-Gesetzes wird auch als Umgebungsgleichung bezeichnet:

P/A = σ _* (T⁴ – T₀⁴)

mit der Stefan-Boltzmann-Konstanten σ = 5,670 10 ^-8 [W m^-2 K^-4],

P = Strahlungsleistung in [W], A = Fläche [m²], T und T₀ Temperaturen in [K]

In der üblicherweise dargestellten Form lautet das Stefan-Boltzmann-Gesetz:

P/A = σ _* T⁴

Diese Form des Stefan-Boltzmann-Gesetzes stellt den astronomischen Spezialfall für eine Umgebungstemperatur T₀ von 0 Kelvin dar.

Das Stefan-Boltzmann-Gesetz stellt somit eine feste Beziehung zwischen Strahlungsleistung, Oberfläche und Temperatur eines Schwarzen Körpers her, oder anders ausgedrückt, es setzt für eine konkrete TEMPERATUR eine flächenkonstante SPEZIFISCHE Strahlungsleistung (P/A=konst. @A) voraus. Denn im S-B-Experiment hat ein Schwarzer Körper eine genau DEFINIERTE Temperatur, bei der er über seine gesamte Oberfläche ZEITGLEICH mit einer DEFINIERTEN konstanten Leistung abstrahlt.

Lediglich im ersten Bericht des IPCC von 1992 wird der „natürliche atmosphärische Treibhauseffekt“ noch irgendwie beschrieben; alle Folgeberichte beziehen sich dann nur noch auf seine vorgebliche Wirkungsweise durch heiße Luft (=„klimaaktive Gase“). Eine exakte Herleitung dieses „natürlichen atmosphärischen Treibhauseffektes“ sucht man auch in der physikalischen Literatur vergebens (Gerlich & Tscheuschner 2009). Selbst im Internet beschränkt sich die aktuelle Information über den atmosphärischen Treibhauseffekt auf wenig konkrete Allgemeinplätze und verallgemeinerte Flussdiagramme; das amerikanische Wikipedia bietet immerhin noch eine dünne Erklärung mit konkreten Zahlenwerten an, Zitat mit Hervorhebungen:

“…If an ideal thermally conductive blackbody were the same distance from the Sun as Earth is, it would have a temperature of about 5.3 °C. However, because Earth reflects about 30% of the incoming sunlight, this idealized planet’s effective temperature (the temperature of a blackbody that would emit the same amount of radiation) would be about −18 °C. The surface temperature of this hypothetical planet is 33 °C below Earth’s actual surface temperature of approximately 14 °C. The mechanism that produces this difference between the actual surface temperature and the effective temperature is due to the atmosphere and is known as the greenhouse effect…”

Dank an den neutralen Google-Übersetzer mit einer [Korrektur]:

„… Wenn ein idealer wärmeleitender Schwarzkörper genauso weit von der Sonne entfernt wäre wie die Erde, hätte er eine Temperatur von etwa 5,3 ° C. Da die Erde jedoch ungefähr 30% des einfallenden Sonnenlichts reflektiert, würde die effektive Temperatur dieses idealisierten Planeten (die Temperatur eines schwarzen Körpers, der dieselbe Strahlungsmenge [-leistung] emittieren würde) ungefähr –18 ° C betragen. Die Oberflächentemperatur dieses hypothetischen Planeten liegt 33 ° C unter der tatsächlichen Oberflächentemperatur der Erde von ungefähr 14 ° C. Der Mechanismus, der diese Differenz zwischen der tatsächlichen Oberflächentemperatur und der effektiven Temperatur erzeugt, ist atmosphärisch bedingt und wird als Treibhauseffekt bezeichnet. “

Anmerkung: Auch hier auf Wikipedia sind bereits gewisse „Anpassungen“ an den „menschengemachten“ Klimawandel zu erkennen. Ursprünglich wurde der Beitrag eines „natürlichen atmosphärischen Treibhauseffektes“ (THE) zur Globaltemperatur nämlich als Differenz von 33°C zwischen den -18°C aus der konventionellen globalen S-B-Ableitung und einer vorgeblich „gemessenen“ globalen Durchschnittstemperatur von 15°C bestimmt (Sekundärzitat auf Kiehl et al. (1997) für diese Globaltemperatur hier auf Seite 7 im 2. Absatz). Auf Wikipedia wird durch deren Reduzierung auf 14°C (THE32°C) nunmehr Platz für einen „anthropogenen“ Temperaturanstieg von etwa 1°C geschaffen, wodurch der Temperaturanstieg seit Beginn der Industrialisierung allein dem anthropogenen CO₂-Ausstoß zugerechnet wird.

Die WMO gibt die globalen Absoluttemperaturen für die vergangenen Jahre mit (14,57°C@2014, 14,76°C@2015, 14,83°C@2016, 14,76°C@2017 und 14,68°C@2018) an und bleibt damit sogar noch unter der Globaltemperatur von Kiehl et al. (1997).

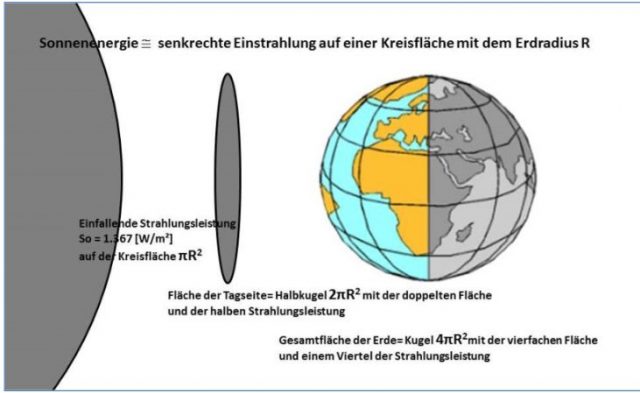
Ein „natürlicher atmosphärischer Treibhauseffekt“ scheint also heutzutage zum gesicherten allgemeinen Glaubensrepertoire zu gehören und bedarf offenbar keiner tieferen physikalischen Erklärung mehr. Versuchen wir trotzdem einmal, die dargestellten Eckwerte zu rekonstruieren und ihre Relevanz zu hinterfragen. Wenn wir in die Solarkonstante “S₀” (= 1.367 W/m²) in das S-B-Gesetz einfügen, dann erhalten wir für die temperaturwirksame Sonneneinstrahlung:

S_{0 *} (1-α) = P/A = σ _* T⁴ mit α = Albedo der Erde und (P/A=konst. @A)

Solange wir es mit selbststrahlenden Sternen und einheitlichen Werten der spezifischen Strahlungsleistung auf den betrachteten Flächen (P/A=konst.) zu tun haben, ist die Anwendung des Stefan-Boltzmann-Gesetzes trivial. Sehr viel komplizierter wird es, wenn wir uns mit einem passiv „beheizten“ Planeten wie der Erde (spezifische Einstrahlungsleistung = Funktion von Tageszeit und geographischer Breite) befassen. Denn das Stefan-Boltzmann-Gesetz muss vor einer jeglichen Mittelwertbildung für das S-B- Temperaturäquivalent zuerst auf die örtlich konstanten Individualwerte der spezifischen Strahlung angewendet werden (Gerlich 1995), wie auch meine nachstehende Ungleichung nachweist:

mit S_i = individuelle spezifische Strahlungsleistung (P_i/A_i) und
T_S-B = Gemittelte Durchschnittstemperatur aus den individuellen S-B-Temperaturäquivalenten
T_M = Durchschnittstemperatur als aus einer gemittelten Strahlungsleistung

Nur wenn die einzelnen S-B Temperaturäquivalente vor der Mittelwertbildung aus der jeweiligen örtlichen Strahlungsleistung (S_i=P_i/A_i=konst. @ A_i) berechnet werden, ergibt sich ein korrektes
Mittel für die Temperatur auf der Tagseite. Im S-B-Experiment strahlt ein Schwarzer Körper bei konstanter Temperatur mit einer konstanten Flächenleistung (P/A=konst. @A), aufgrund der Versuchsanordnung praktisch als Quasi-2-D-Strahler. Für eine Anwendung des S-B-Gesetzes auf eine beliebige bestrahlte Fläche „A“ ergibt sich also das folgende Dilemma:

Für die Anwendung des Stefan-Boltzmann-Gesetzes auf die passiv bestrahlte Erde ergibt sich damit die folgende Situation für das rechnerische S-B-Temperaturäquivalent (S-B-T):

S-B-T Einstrahlung @ πR²: Sonneneinstrahlung auf einer Kreisfläche mit (A = πR²) und (P/A=konst.)

=> eine direkte S-B Anwendung ist möglich

S-B-T Tagseite @ 2πR²: Sonnenstrahlung auf der Tagseite der Erde mit (A = 2πR²) und (P/A≠konst.)

=> eine S-B Anwendung ist lediglich auf Teilflächen mit (P/A=konst.) möglich

S-B-T Abstrahlung @ 4πR²: Mittelung der solaren Einstrahlung über die gesamte Erdoberfläche mit (A = 4πR²) und (P/A≠konst. @ Tagseite mit 2πR²) sowie (P/A=0 @ Nachtseite mit 2πR²)

=> es ist keine S-B-Anwendung über die Gesamtfläche der Erde möglich, denn die Nachtseite erfüllt die S-B-Bedingung eines gemeinsamen thermischen Gleichgewichtes NICHT (für die Abstrahlung @ 4πR² gilt vielmehr die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes)

Schaunmeralsomalgenauhin:

Eine S-B konforme Temperaturberechnung muss demnach additiv über die Mittelung aller Flächenelemente mit gleicher spezifischer Sonneneinstrahlung auf der Tagseite der Erde erfolgen, wie die nachfolgende Abbildung zeigt.

Berechnungsschema:

Lotrechter Sonnenstand auf dem Äquator,
Berechnung des S-B-Temperaturäquivalents aus der
lokalen solaren Einstrahlung auf Mantelringen mit dem Radius r_i
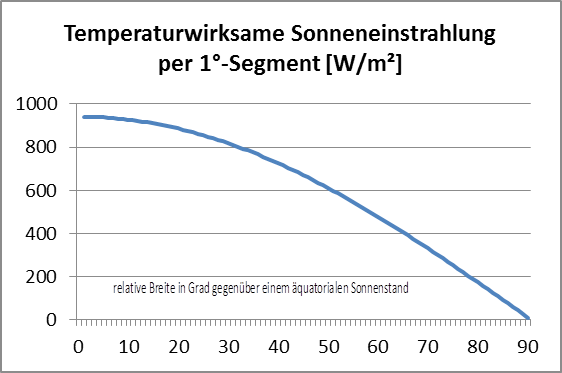
und dem Zenitwinkel _i nach der Formel: S_i = S_{0 *} (1-α) _* cos ?_i = σ _* T_i ⁴_S-B
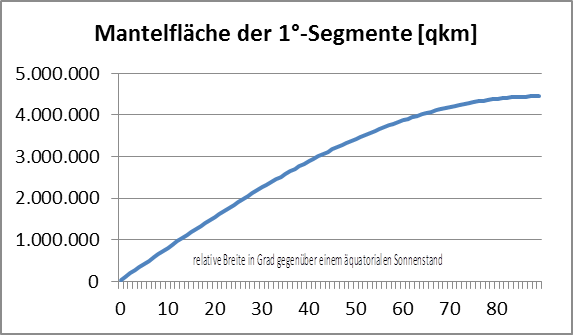
Summation von 0°-90° über konzentrische Mantelringe von 1° Breite

Die Gleichung für einen flächengewichteten Mittelwert der örtlichen S-B-Individualtemperaturen lautet dann:

Mittelwert der S-B-Temperaturäquivalente auf der Tagseite der Erde

Die Berechnungen für die nachfolgenden Abbildungen beruhen auf einem mittäglich zenitalen Sonnenhöchststand in äquinoktialer Position und wurden in konzentrischen 1°-Ringen des individuelle Zenitwinkels ?_i von 0° bis 90° gegenüber einem äquatorialen Sonnenstand durchgeführt:

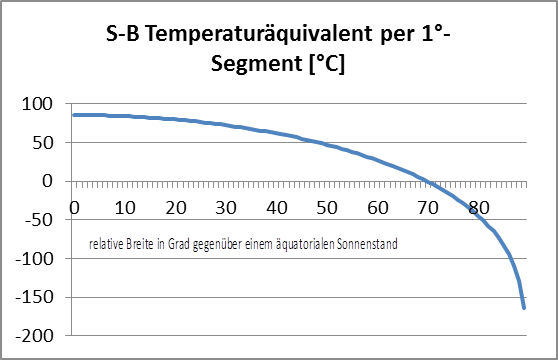
Dabei wurden die hemisphärischen Strahlungswerte S_i und das zugehörige S-B-Temperaturäquivalent T_i für die jeweilige Ringmitte ermittelt, also beispielsweise bei 1,5° für den Ring von 1°-2°:

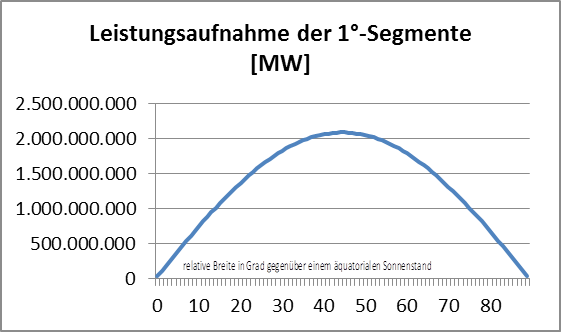
Die Berechnungen für diese Grafiken stellen lediglich eine Momentaufnahme bei konstantem äquatorialem Sonnenstand dar und repräsentieren für keine Position auf der Taghalbkugel der Erde einen vollen Tageszyklus. Wir berechnen trotzdem einmal einen flächengewichteten Temperaturdurchschnitt aus den konzentrischen 1°-Mantelringen der Tagseite für individuelle Zenitwinkel von 0° bis 90° bei einem äquatorialen Sonnenstand:

mit T_i=S-B-Temperaturäquivalent und F_i=Fläche eines 1°-Mantelrings mit r_i und ?_i (= ?_ri +/- 0,5°)

Anmerkung: Dieses Ergebnis für ein durchschnittliches hemisphärisches S-B-Temperaturäquivalent dürfte sich noch etwas erhöhen, wenn die Mantelringe schmaler gewählt werden.

Dieses Flächenmittel für das hemisphärische S-B-Temperaturäquivalent von 14,03 °C kommt schon recht nahe an die vorgeblich „gemessene“ globale Durchschnittstemperatur (NST) heran (S. dazu auch die obige Anmerkung zur Wikipedia-Übersetzung für den THE). Aus der „Brennglasperspektive“ der obigen hemisphärischen Summation erscheint die „Klimaküche“ zwischen den Wendekreisen gegenüber einem normalen Tagesverlauf unterrepräsentiert, während die randlichen Mantelringe in hohen relativen Breiten mit ihren negativen Celsius-Temperaturen überrepräsentiert sind. Aber die hier vorgestellte Approximation wird durch das Ergebnis von Gerlich and Tscheuschner (2009) gestützt, die eine Stefan-Boltzmann-Integrallösung für die Durchschnittstemperatur der gesamten Erdoberfläche (4R²) hergeleitet hatten. Diese physikalische Globaltemperatur T_phys beträgt -129 °C, respektive 144,15 °K für die gesamte Erdoberfläche (4R²). Wir haben aber gesehen, dass lediglich die Tagseite der Erde (2R²) im Strahlungsgleichgewicht zwischen Sonne und Erde mit dem Stefan-Boltzmann-Gesetz betrachtet werden darf. Von daher muss diese Lösung von Gerlich and Tscheuschner (2009) auf die Tagseite der Erde (2R²) reduziert werden:

Lösung G&T _* 4πR²

Die Differenz zwischen der hemisphärischen Summation über das zenitabhängige S-B-Temperaturäquivalent T_i und der korrigierten Lösung von G&T (2009) verwundert nicht. Vielmehr dürfte diese korrigierte Integrallösung den Grenzwert (zu:

(=15,15°C)

Die Temperaturgenese auf unserer Erde erfolgt also ausschließlich auf deren Tagseite (@ 2R²). Die Ableitung einer „theoretischen“ Durchschnittstemperatur für die gesamte Erdoberfläche muss also eine Fiktion bleiben, weil das Stefan-Boltzmann-Gesetz auf der Nachtseite der Erde nicht anwendbar ist, jedenfalls nicht in einem Zusammenhang mit der direkten Sonneneinstrahlung. Vielmehr gilt dort, wie natürlich auch auf der Tagseite (also insgesamt @ 4R²), die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes für die örtliche Abstrahlung aufgrund der thermischen Interaktion mit den globalen Wärmespeichern (Atmosphäre und Ozeane).

Die mit dem S-B Gesetz ermittelten Durchschnittstemperaturen für die Tagseite der Erde T_HEM und T_phys-korr lassen keinerlei Raum für einen „natürlichen atmosphärischen Treibhauseffekt“ von 33 °C, sondern sind vielmehr ein Beweis für meinen hemisphärischen Stefan-Boltzmann Ansatz.

—————————————

Danksagung: Der Autor bedankt sich bei der EIKE-Redaktion für Korrekturen am Text und fachliche Hinweise zur vorgeblich „gemessenen“ Globaltemperatur.

Schlussbemerkungen: Alle Strahlungswerte für die hier vorgestellten Berechnungen wurden aus den globalen Durchschnittswerten von KIEHL and TRENBERTH (1997) abgeleitet. Wegen der bereits darin enthaltenen Rundungen auf volle W/m² und weiteren Rundungen in den nachfolgenden Berechnungen, sowie unterschiedlichen Werten für die Albedo der Erde, kann es zu Differenzen gegenüber direkt abgeleiteten Strahlungswerten und S-B Temperaturäquivalenten kommen; das gilt beispielsweise für die „natürliche“ Temperatur der Erde von -18 °C respektive -19 °C.

(*) Die versprochene Auflistung meiner hemisphärischen S-B-Beiträge hier auf EIKE:

1. 23. Januar 2017: Über einen vergeblichen Versuch, unsere Welt vor der Dekarbonisierung zu retten
2. Februar 2017: Wer im Treibhaus sitzt…
3. 16. Februar 2017: Nachdem sich der Rauch verzogen hat: Stefan-Boltzmann auf den Punkt gebracht
4. 23. Juni 2017: Noch ein paar Fragen zum „natürlichen“ atmosphärischen Treibhauseffekt
5. Juli 2017: Beweist die Temperatur des Mondes den hemisphärischen Stefan-Boltzmann Ansatz?
6. 19. August 2017: Machen wir mal ein Gedankenexperiment: Es gibt gar keine Erde!
7. 26. November 2017: Rückblick: Ein Jahr hemisphärischer Stefan-Boltzmann Ansatz
8. 30. November 2017: Nicht immer passt wirklich alles zusammen
9. 22. Februar 2018: Eine barrierefreie Erklärung für die hemisphärische Temperaturgenese auf unserer Erde
10. Mai 2018: Fangen wir mit dem Stefan-Boltzmann-Gesetz noch einmal ganz von vorne an
11. 29. Juli 2019: Safety First: Zum besseren Verständnis meiner hemisphärischen Energiebilanz

Es ist abschließend anzumerken, dass es sich beim „Weber’schen Hemisphärenansatz“ um ein völlig neues Modell für die Temperaturgenese auf unserer Erde handelt. Mein Modell konkurriert also auf gleicher Ebene mit allen bestehenden Modellen, die diese Temperaturgenese ebenfalls zu beschreiben suchen. Eine Skandalisierung meines Modells anhand von bekanntem Lehrbuchwissen, in dem diese konkurrierenden Modelle dargestellt werden, ist also wissenschaftlich absolut unzulässig. Konkurrierende Modelle können sich untereinander weder bestätigen noch widerlegen; das geht nur über deren gemeinsame physikalische Grundlagen. Mein hemisphärischer Stefan-Boltzmann-Ansatz kann also jederzeit über die bestehenden grundlegenden physikalischen Gesetze widerlegt werden. Alle meine Kritiker sind daher höflich aufgefordert, meine bereits mehrfach erhobene Widerlegungsanforderung über einen physikalischen Gleichwertigkeitsnachweis von Tag und Nacht zu erbringen, Zitat:

„Wenn also wissenschaftlich eindeutig nachgewiesen würde, dass die Gleichsetzung der Energiebilanz unserer Erde (Fläche einer Kugel) mit der strengen thermischen Gleichgewichtsforderung des Stefan-Boltzmann Gesetzes für die bestrahlte Fläche (Halbkugel) physikalisch korrekt ist, dann bin ich tatsächlich widerlegt.“

Die Skandalisierungen meiner Erkenntnisse erheben mich ungewollt in den Status von solchen naturwissenschaftlichen Größen, die mit bahnbrechenden wissenschaftlichen NEUERUNGEN gegen den Mainstream angeschwommen sind. In meinem Fall müssten aber hunderttausende von Menschen mit einer akademischen Ausbildung in Physik meiner Korrektur von BESTEHENDEM unmittelbar folgen können; von Abiturienten im gymnasialen Physik-Leistungskurs einmal ganz zu schweigen.
Denn mein hemisphärischer Stefan-Boltzmann-Ansatz basiert lediglich auf der strengen physikalischen Randbedingung der GLEICHZEITIGKEIT im Stefan-Boltzmann-Gesetz, die dort seit Stefan und Boltzmann fest verankert ist und durch das mathematische Gleichheitszeichen repräsentiert wird. Auch der gemeine Physikprofessor mag daher das Stefan-Boltzmann-Gesetz noch nicht vollständig durchdrungen haben. Der Lernhelfer zum S-B-Gesetz könnte vielleicht auch ihm eine Hilfestellung zum besseren Verständnis geben – und „Simsalabim“ ist der auf einer „Gegenstrahlung“ aufbauende „natürliche atmosphärische Treibhauseffekt“ einfach verschwunden!