Safety First: Zum besseren Verständnis meiner hemisphärischen Energiebilanz
Denn ein „natürlicher atmosphärischer Treibhauseffekt“ wurde niemals wissenschaftlich nachgewiesen, weder experimentell noch theoretisch. Vielmehr basiert selbst seine theoretische Ableitung über die Schwarzschild-Gleichung und die Strahlungstransfergleichungen auf den ominösen minus 18° Celsius aus der konventionellen (und falschen) S‐B Schwarzkörperberechnung, gemittelt über die gesamte Erdoberfläche, und deren rechnerischer Differenz von 33° Celsius zu einer global gemessenen Mitteltemperatur (Near Surface Temperature = NST) von plus 14,8° Celsius.
Im letzten Artikel über meinen hemisphärischen Stefan-Boltzmann Ansatz hier auf EIKE mit dem Titel „Fangen wir mit dem Stefan-Boltzmann-Gesetz noch einmal ganz von vorne an“ hatte ich am Ende eine hemisphärische Gleichung für die globale Energiebilanz unserer Erde aufgestellt:
[1] (IN = 940 W/m² * R2) = (OUT = 235 W/m² * 4 R2) @ NST (= 14,8 °C)
Meine abschließende Erklärung lautete dort: „Wir haben hier auf unserer Erde also eine ausgeglichene globale Strahlungsbilanz bei einer konstanten global gemessenen Durchschnittstemperatur, wie immer diese auch ermittelt worden sein mag oder vielleicht erst viel später einmal korrekt ermittelt werden wird. Diese global gemessene Durchschnittstemperatur repräsentiert damit den durchschnittlichen globalen Netto-Wärmeinhalt von Atmosphäre und Ozeanen auf unserer Erde, um den herum permanent die hemisphärische Einstrahlung und die globale Abstrahlung erfolgen.“
Offenbar konnten die geschätzten Kommentatoren mit der Umgebungsgleichung des Stefan-Boltzmann-Gesetzes in der Form „P/A = * (T4-T04)“, die dieser Betrachtung zugrunde liegt, aber recht wenig anfangen, möglicherweise auch deshalb, weil es sich um ein richtiges Zitat aus einem „falschen Buch“ gehandelt haben soll. Und „falsche Bücher“ sind für wahre Gläubige bekanntermaßen höchst verwerflich. Immerhin hatte dort ein freundlicher Chronist die Zahl meiner häretischen Artikel für eine spätere IPCC-Inquisition bereits genauestens dokumentiert.
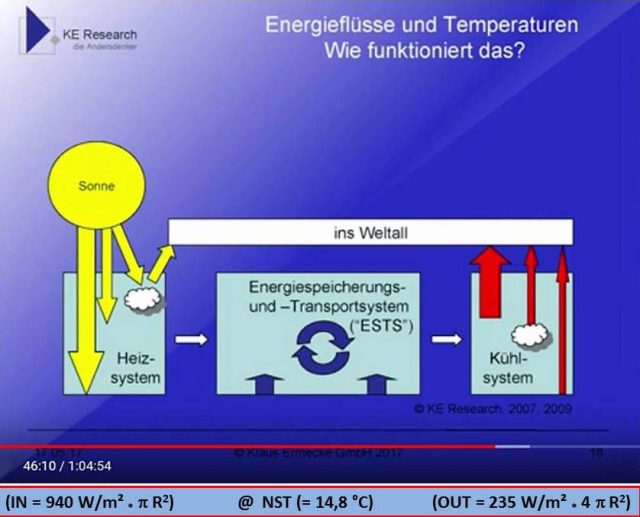
Aber eigentlich richten sich meine Artikel ja an interessierte Laien und ergebnisoffen denkende Fachleute: In den Kommentaren zu einem anderen EIKE-Artikel wurde gerade in einem Link auf den Vortrag von Klaus Ermecke „Energiepolitik im Konzeptnebel?“ verwiesen. Dort wiederum findet sich ab Minute 46:10 ein interessantes Diagramm, das die oben in Gleichungsform beschriebene Strahlungssituation auf unserer Erde grafisch verdeutlicht. Die nachstehende Abbildung von Herrn Ermecke ist daher für ein besseres Verständnis meiner Ausführungen zum hemisphärischen Stefan-Boltzmann Ansatz hervorragend geeignet:
Abbildung 1: Chart aus dem Vortrag von Klaus Ermecke „Energiepolitik im Konzeptnebel?“ © KE Research 2007/2009 mit freundlicher Genehmigung
Diese Abbildung von Ermecke hat gegenüber den bekannten Darstellungen von Kiehl und Trenberth zwei Vorteile und einen großen Nachteil: Einerseits beschränkt sie sich auf eine grundsätzliche Betrachtung der beiden wesentlichen Strahlungsvorgänge (IN und OUT) und beinhaltet insbesondere auch die Wärmespeicherung, andererseits fehlt hier eine Quantifizierung der Strahlungsflüsse. Diesen fehlenden Strahlungsflüssen ist nun mit meiner hemisphärischen Energiebilanz [1] sehr leicht abzuhelfen. Dort wird die temperaturwirksame hemisphärische Sonneneinstrahlung mit der durchschnittlichen globalen Abstrahlung gleichgesetzt. Und der Wärmeinhalt der globalen Zirkulationen (Atmosphäre und Ozeane) wird über die gemessene Durchschnittstemperatur unserer Erde (NST) definiert: Die NST wird üblicherweise mit 14,8 Grad Celsius angegeben. Sie stellt eine langjährige globale Durchschnittstemperatur dar, bei der im Idealfall alle Energieflüsse (IN und OUT) über den Tag- und Nachtverlauf sowie die Breitenverteilung und der Jahresverlauf aller benutzten Meßstationen bereits korrekt herausgemittelt worden sein sollten.
Der quasi-konstante NST-Wert wurde also bereits um die langjährige Ein-und Abstrahlung bereinigt und hat überhaupt nichts mehr mit der globalen Strahlungsbilanz zu tun. Er repräsentiert vielmehr die natürlichen Wärmespeicher unserer Erde, deren eigener Wärmefluss aus dem Erdinneren dabei vernachlässigbar ist. Wenn wir also bei der NST in einer langjährigen Betrachtung alle tages- und jahreszeitlich variablen Prozesse auf unserer Erde als durchschnittlich ausgeglichen voraussetzen können, dann lassen sich die Begrifflichkeiten aus der obigen Abbildung von Ermecke und mein hemisphärischer Ansatz für die globale Energiebilanz unserer Erde folgendermaßen zusammenfügen:
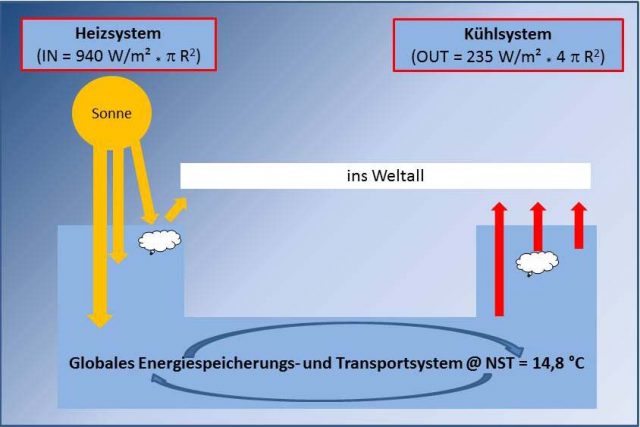
Wir können hier also folgende grafisch dargestellten Begrifflichkeiten und die physikalischen Größen aus der hemisphärischen Energiebilanz einander direkt zuordnen:Heizsystem: Die Sonne liefert auf der Tagseite der Erde netto 940 W/m2 temperaturwirksame Strahlung auf einer Kreisfläche von R2 (mit dem Erdradius „R“).
Energiespeicherungs- und Transportsystem: Die NST von 14,8 °C repräsentiert den global gemittelten Netto-Wärmeinhalt von Atmosphäre und Ozeanen im Gleichgewicht von Ein- und Abstrahlung.
Kühlsystem: Die Erde strahlt im Temperaturgleichgewicht (NST=const.) durchschnittlich 235 W/m2 über ihre Gesamtfläche 4R2 in den Weltraum ab.
Damit ergibt sich in Kombination der Darstellung und Begrifflichkeiten von Ermecke mit Gleichung [1] das folgende Bild:
Die Umgebungsgleichung des Stefan-Boltzmann-Gesetzes lautet in einer etwas ausführlicheren Form „S = S-S0 = * (T4-T04)“. Und jetzt wird hoffentlich auch deutlich, dass es entscheidend darauf ankommt, die S-B Umgebungstemperatur T0 bei allen Berechnungen korrekt zu definieren. Wenn man nämlich die Temperatur des Weltalls als Umgebungstemperatur der globalen Temperaturmeßstationen definiert, dann gelangt man zum konventionellen S-B Ansatz mit minus 18°C und einem „natürlichen atmosphärischen Treibhauseffekt“ von 33 Grad Celsius.Aber wo stehen eigentlich die Thermometer der Messstationen für die Berechnung der NST, etwa am Rande des Weltraums?
Nein, keine der globalen Temperatur-Messstationen steht am Rande des Weltraums mit seiner Umgebungstemperatur von fast null Grad Kelvin. Selbst in der Polarnacht der jeweiligen Winterhemisphäre bleibt die gemessene Temperatur deutlich oberhalb von minus 100°C. Das T0 der S-B Umgebungsgleichung repräsentiert also die örtliche Temperatur von Atmosphäre und Ozeanen in der Umgebung der jeweiligen Messstation. Und im langjährigen Durchschnitt über alle Messstationen auf der Erde gilt dann folglich, dass diese S-B Umgebungstemperatur gleich der global gemessenen Durchschnittstemperatur sein muss, also „T0 = NST“.
Es ist schon sehr erstaunlich, wie sich der Absolute Nullpunkt einfach so in die konventionelle S-B Temperaturberechnung für unsere Erde „einschleichen“ konnte, obwohl er in der Umgebung der Temperaturmessstationen gar nicht vorkommt. Dieser Wert hat sich nämlich allein aus einer Betrachtung unserer Erde vom Weltraum aus ergeben. Und nach dem Stefan-Boltzmann-Gesetz müsste ein selbstleuchtender Stern, der mit konstant 235 W/m2 abstrahlt, tatsächlich eine Temperatur von minus 18°C aufweisen. Daraus entsteht das Paradoxon, dass, aus dem Weltraum betrachtet, unsere Erde zwar eine gemessene Mitteltemperatur von 14,8°C besitzt, aber nur mit durchschnittlich 235 W/m² anstatt mit 390 W/m² abstrahlt. Durch die Einführung eines „natürlichen atmosphärischen Treibhauseffektes“ (THE), der durch eine sogenannte „atmosphärische Gegenstrahlung“ verursacht werden soll, wird dieses Paradoxon nun in die Erdatmosphäre verlegt, ohne es aufzulösen. Dieser THE soll nämlich die Erdoberfläche zusätzlich um 33 °C von minus 18°C auf 14,8°C erwärmen, ohne dass sich die globale Abstrahlung von 235 W/m² dadurch verändert, Zitat (mit leicht abweichenden Strahlungswerten):
„Die Erdoberfläche strahlt Wärme mit durchschnittlich 390 Watt pro Quadratmeter ab. Das entspricht der Wärmeabstrahlung eines sog. Schwarzen Körpers bei 15°C. In 70 km Höhe strahlt die Erde nach Absorption durch Treibhausgase und Wolken innerhalb der Atmosphäre nur noch Wärme mit durchschnittlich 240 Watt pro Quadratmeter ab. Das entspricht der Wärmeabstrahlung eines sog. Schwarzen Körpers bei -18°C. Die Differenz zwischen Boden und 70 km beträgt 150 Watt pro Quadratmeter und 33°C. Das ist die sog. Differenz für den natürlichen Treibhauseffekt.“
Dieses Zitat lässt sich allerdings auch umkehren:
Die Strahlungsdifferenz zwischen Erdboden und der Atmosphäre in 70 km Höhe beträgt angeblich 150 (ich rechne mit 155) Watt pro Quadratmeter und 33°C. Und die Abstrahlung eines Schwarzen Körpers mit einer beliebigen Temperatur (T) beträgt bei einer Umgebungstemperatur (T0 ungleich 0°K) nur dessen Strahlungsdifferenz entsprechend der S-B Umgebungsgleichung „S = * (T4-T04)“. Nach der Umgebungsgleichung des Stefan-Boltzmann-Gesetzes kann ein Schwarzer Körper also mit einer deutlich geringeren Leistung abstrahlen, als es das Stefan-Boltzmann-Gesetz in dem Spezialfall (T0=0°K) mit „P/A=*T4“ vorgibt, denn es kommt dabei allein auf seine Umgebungstemperatur T0 an. Dabei gilt, dass diese Strahlung umso geringer wird, je kleiner die Temperaturdifferenz ist.
Und nun wenden wir den Blickwinkel des obigen Zitates auf die S-B Umgebungsgleichung an:
Die Atmosphäre in 70 km Höhe strahlt bei (T0=minus18°C) mit 240 (ich rechne mit 235) W/m² in den Weltraum ab. Diese rechnerische Differenz zum Wärmeinhalt der oberflächennahen Atmosphäre und der Ozeane mit durchschnittlich (T=14,8°C) entspricht dann nach der Umgebungsgleichung des Stefan-Boltzmann-Gesetzes 150 (ich rechne mit 155) W/m². Bei diesen 150/155 W/m² handelt es sich also keineswegs um einen Wärmefluss vom Kälteren zum Wärmeren („Gegenstrahlung“), sondern um den Wärmefluss zwischen einem warmen und einem kälteren Körper nach der S-B Umgebungsgleichung. Und dazu bedarf es lediglich einer thermischen Schichtung der Erdatmosphäre, so wie sie sich nach obigem Zitat ja auch tatsächlich darstellt.
Die durchschnittliche Abstrahlung unserer Erde von 235 W/m2 (@ 4R2) steht bei einer durchschnittlichen „Speichertemperatur“ von 14,8°C von Atmosphäre und Ozeanen also im thermischen Gleichgewicht mit dem solaren Klimaantrieb von netto 940 W/m2 (@ R2). Und diese Beziehung lässt keinerlei Raum für einen „natürlichen atmosphärischen Treibhauseffekt“.
Übrigens findet man bereits bei Gerlich(†), und später auch bei Gerlich und Tscheuschner in der theoretischen Herleitung einer globalen Durchschnittstemperatur mit dem Stefan-Boltzmann-Gesetz eine Aufteilung der Strahlungsflüsse für die Tag- und Nachtseite der Erde. So wird in einem Vortragsskript von Professor Gerlich (1995), dort auf Seite 19, ein globaler S-B Ansatz mit einer breitenabhängigen Strahlungsmenge (σT4 = ν ⋅S⋅ cosϑ) auf der Tagseite und 0 W/m² auf der Nachtseite vorgestellt. Mit diesen beiden Randbedingungen wird dann allerdings über „0 bis 2π“ integriert, also über den gesamten Tagesverlauf von 24 Stunden. Das Ergebnis ist zwangsläufig eine konventionelle Mittelung der S-B Individualtemperaturen über die gesamte Erdoberfläche mit einem globalen Durchschnittswert von minus 129 °C bei 30% Albedo (dort Seite 20). Dieses Modell bildet einen einseitig bestrahlten und thermisch nicht speicherfähigen Schwarzkörper ab. Dasselbe Ergebnis findet man später auch bei Gerlich und Tscheuschner (2009), beispielsweise in Kapitel 3.7.4 der deutschen Übersetzung.
Die Temperaturgenese durch die Sonneneinstrahlung erfolgt aber ausschließlich auf der Tagseite der Erde (Integration über 0 bis π), während die Temperatur auf der Nachtseite der Erde (π bis 2π) wegen des Wärmeinhalts von Atmosphäre und Ozeanen niemals auf eine Temperatur von 0°Kelvin (entsprechend 0 W/m²) absinken kann. Das oben beschriebene Integral „0 bis 2π“ bildet also nicht die tatsächlich vorliegende Situation auf unserer Erde ab und ist deshalb wohl eher auf ihren Trabanten anwendbar (hier auf den Seiten 6 bis 8).
Fokussieren wir jetzt einmal auf die Tagseite der Erde: Die -129 °C aus der Berechnung von Professor Gerlich entsprechen 144°K und sind das rechnerische Temperaturmittel für die gesamte Erdoberfläche (nachfolgend FE) aus den individuellen S-B Ortstemperaturen. Folglich gilt:
Mittelung von T @ FE: (Σi=1n Ti + Σj=1m Tj)/(n+m) = 144°K
mit den Temperaturen Ti(i=1 bis n) auf der Nachtseite und Tj(j=1 bis m) auf der Tagseite
(n+m) = Anzahl aller Einzelwerte auf der Tag- und Nachtseite, die zur Mittelung beitragen
Tag- und Nachtseite der Erde sind symmetrische Halbkugeln, daher gilt (i=j) und (n=m):
für die Nachtseite @FE/2 gilt: Σi=1n Ti = 0°K
damit ergibt die Mittelung @ FE : (Σj=1m Tjj)/(2m) = 144°K
für die Tagseite @FE/2 gilt dann: (Σj=1m Tjj)/(m) = 2 * 144°K = 288°K = 15°C
Oder ganz einfach ausgedrückt: Bei der Mittelung von Professor Gerlich stammen alle Temperaturen ungleich Null von der Tagseite der Erde. Wenn wir uns bei der Durchschnittsbildung also auf diese Hälfte der Erdoberfläche beschränken, dann verdoppelt sich das Ergebnis auf 15°C. Und damit wären wir dann wieder bei meinem hemisphärischen Stefan-Boltzmann Ansatz…
Hier die beiden PDFs: