Experimentelle Verifikation des Treibhauseffektes
1. Einführung
In der ersten Mitteilung (1 hier ) wurde eine neuartige Apparatur vorgestellt, die im Gegensatz zu den bisher bekannten Untersuchungsmethoden nicht die austretende IR-Strahlung (Transmission), sondern die IR-Gegenstrahlung (Treibhauseffekt) von IR-aktiven Gasen untersucht. Die Apparatur enthält als wesentliche Bestandteile eine sogenannte Erd-Platte und in einem großen Abstand eine Aerosol-Platte, die stellvertretend für die Erdoberfläche und für eine Wolkenschicht stehen. Bei einem ersten Test mit Propan als Modell-Treibhausgas wurde gefunden, dass dieses Gas eine bereits vorhandene, konstruktionsbedingte Gegenstrahlung EG unter bestimmten Voraussetzungen erhöhen kann. Diese Untersuchung wurde nun mit Methan, CO2, Lachgas, Butan und Freon 134a wiederholt. Hierzu wurde die auf 16 °C temperierte Apparatur mit 1,3 Vol.-% des IR-Gases gefüllt und danach nur die Aerosol-Platte schrittweise bis auf – 18 °C abgekühlt. Bei jedem Abkühlungsschritt wurde die Heizleistung QE ermittelt, die für eine konstante Temperatur der Erd-Platte von 16,09 °C erforderlich ist (experimentelle Daten siehe Kap. 4).
Diese Art der Versuchsdurchführung wird „Abkühlungs-Modus“ genannt, da die Temperatur der Aerosol-Platte schrittweise gesenkt wird. Mit dieser Technik lässt sich die wechselseitige Beeinflussung von einer IR-Gas-Strahlung mit der Hintergrundstrahlung der Aerosol-Platte untersuchen. Bei der alternativen Versuchsdurchführung, dem „Konzentrations-Modus“, werden die Strahlungen der IR-Gase bei konstanten Temperaturen aber unterschiedlichen Konzentrationen der Gase analysiert. Hier ist von vornherein die Aerosol-Platte viel kälter als ihre Umgebung. Dieses Verfahren ist besser geeignet, die konzentrationsabhängigen Emissionsgrade der IR-Gase zu ermitteln, worüber in den folgenden Mitteilungen berichtet werden soll.
Die gefundenen Heizleistungen QE werden über die Temperatur der Aerosol-Platte TH (als T4/108, in Kelvin) in einem Excel-Diagramm aufgetragen (Abb. 1). Die zweite X-Achse TpH in °C dient der Orientierung. Der Übersicht halber werden die einzelnen Messpunkte von + 16 bis – 18 °C nur beim Freon angegeben.
In der ersten Mitteilung (1) wurde abgeleitet, dass die Heizung der Erd-Platte QE zahlenmäßig mit der Strahlungskühlung PE identisch ist. Die Strahlungskühlung PE ist die Energie, die die Erd-Platte als Differenz ihrer IR-Ausstrahlung ME und Empfang einer IR-Gegenstrahlung EG verlieren würde (Gleichung 1). ME ist in dieser Gleichung die IR-Ausstrahlung der Erd-Platte von 396,9 W/m2 (berechnet nach Stefan-Boltzmann, ε = 1).
Um ein Abkühlen der Erd-Platte durch Strahlungskühlung zu verhindern, muss ihr von außen Wärme zugeführt werden. Die Erd-Platte hat eine konstante Temperatur wenn QE = PE ist. Die Y-Achse zeigt somit auch die Strahlungskühlung PE an, die von den IR-Gasen beeinflusst wird.
Gleichung 1:
![]()
Man kann den Treibhauseffekt mit der Strahlungskühlung PE oder mit der Gegenstrahlung EG charakterisieren, da beide Größen, wie in Gleichung 1 angegeben, miteinander verknüpft sind. Aber ACHTUNG! Strahlungskühlung und Gegenstrahlung verhalten sich gegenläufig. Eine starke Gegenstrahlung hat eine geringe Strahlungskühlung zur Folge!
In der Literatur wird die Strahlungskühlung (Gleichung 1) als „effektive Ausstrahlung“ der Erde bezeichnet. Der alternative Begriff „Strahlungskühlung“ zeigt, dass es sich hier um eine Kühlung durch IR-Strahlung handelt. Damit soll deutlicher hervorgehoben werden, dass die Erde noch weitere Kühlungsmöglichkeiten, wie z.B. Wasserverdunstung oder Konvektion, hat.
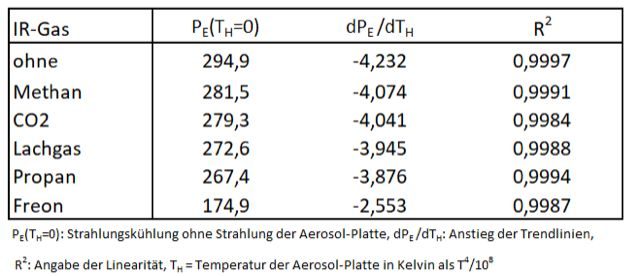
Aus den experimentell ermittelten Messpunkten werden die linearen Excel-Trendlinien berechnet (Tab. 1). Die Trendlinien bestehen aus einem konstanten Teil PE(TH=0) (maximale Strahlungskühlung ohne Gegenstrahlung von der Aerosol-Platte) und einem variablen Teil dPE/dTH (Verlauf der Geraden).
Alle neu untersuchten IR-aktiven Gase zeigen ein ähnliches Strahlungsverhalten wie Propan, aber mit deutlich unterschiedlichen Strahlungskühlungen PE. Damit erweist sich die sehr einfache Versuchsapparatur als durchaus geeignet, den erdnahen Treibhauseffekt zu überprüfen. Die IR-Gase sind in Tab. 1 nach der Wirksamkeit ihres Treibhauseffektes (Abnahme der Strahlungskühlung PE) angeordnet. Eine erste Überraschung ist die Reihenfolge von Methan und CO2. Methan, angeblich ein wesentlich stärkeres Treibhausgas als CO2, erweist sich hier als der schwächere IR-Gegenstrahler. Da bei der aktuellen Versuchsserie der Einfluss der Hintergrundstrahlung im Mittelpunkt stand, soll das unerwartete Resultat der Methan-Strahlung hier nicht weiter kommentiert werden.
In einer weiteren Versuchsserie (dann jedoch im Konzentrations-Modus) wurden alle o.g. IR-Gase noch einmal hinsichtlich ihrer Strahlungsfähigkeit untersucht. Dabei wurde die geringere IR-Strahlung des Methans im Vergleich zum CO2 erneut festgestellt, worüber später berichtet werden soll.
Tabelle 1: Excel-Trendlinien für die Strahlungskühlung der Erdplatte: PE = dPE /dTH ∙ TH + PE(TH=0)
Die Messung im Abkühlungs-Modus macht es möglich, die gegenseitige Beeinflussung der IR-Gas-Strahlung und einer Hintergrundstrahlung in einem Diagramm darzustellen. Dabei wird die Aerosol-Platte als Hintergrundstrahler bezeichnet, da sie sich aus Sicht der Erd-Platte hinter den IR-Gasen befindet. Die Aerosol-Platte scheint für den Treibhauseffekt von geringer Bedeutung, da der größte Teil ihrer Strahlung von den IR-Gasen verdeckt wird und sie also nur im Hintergrund agiert. Das ist eine fundamental falsche Einschätzung, wie im Folgenden gezeigt werden soll.
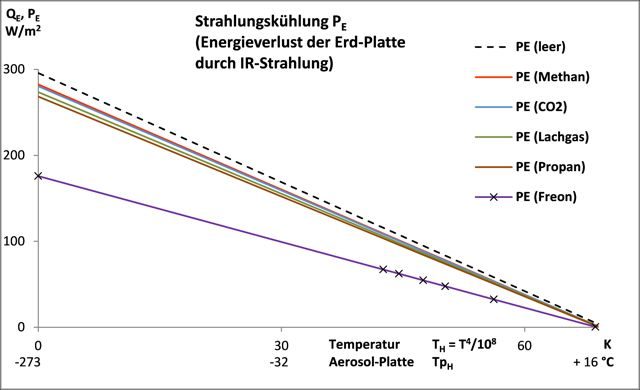
Abb. 1: Beeinflussung der Strahlungskühlung der Erd-Platte PE durch IR-Gase und durch die Temperatur TH der Aerosol-Platte
Aus Abb. 1 ist ersichtlich, dass die Strahlungskühlung der Erd-Platte PE nicht nur von der Wirksamkeit eines IR-Gases, sondern auch von der Temperatur der Aerosol-Platte TH abhängig ist.
Je größer das Strahlungsvermögen eines IR-Gases, desto geringer die Energieabgabe der Erd-Platte durch IR-Strahlung (Strahlungskühlung PE). Andererseits wird die Strahlungskühlung PE aber auch von der Temperatur der Aerosol-Platte beeinflusst, wie an dem abschüssigen (negativen) Verlauf der Trendlinien zu sehen ist. Die Wirkung der IR-Gase kann sogar null werden, wenn Erd- und Aerosol-Platte die gleiche Temperatur haben. Diese Relativierung des Treibhauseffektes durch einen Hintergrundstrahler wurde in der 1. Mitteilung ausführlich abgeleitet.
Die Verringerung des Treibhauseffektes wird durch eine Art Gegenbewegung verursacht. Wenn sich die Strahlung eines Treibhausgases EVG (als Vordergrund-Strahler) erhöht (verringert), verringert (erhöht) sich auch zu einem gewissen Umfang der Teil der Hintergrundes EHG(TH), der die Erd-Platte tatsächlich erreicht (Gleichung 2). Letztendlich ist durch diese Gegenbewegung die Zunahme (Abnahme) der gemeinsamen Gegenstrahlung beider Strahlungsquellen (EG) stets kleiner als die Summe der theoretischen Strahlungen von Vor-und Hintergrund. Vordergrund- und Hintergrundstrahler können als Strahlungskonkurrenten bezeichnet werden, die sich gegenseitig bei der IR-Bestrahlung der Erdoberfläche EG behindern (1).
Gleichung 2:
Dieser Zusammenhang ist von grundsätzlicher Bedeutung und gilt auch für Wolken. Wolken können einerseits je nach Schichtdicke und Wolkenart bis zu 90 % der Sonneneinstrahlung reflektieren (Wolken-Albedo, (2)) und damit die Erde abkühlen. Andererseits verursachen Wolken als IR-Strahler aber auch eine Erwärmung der Erde, was ihre Bewertung bisher so schwierig machte. Die Konkurrenz mit Treibhausgasen verringert nur den Beitrag der Wolken bei der IR-Bestrahlung der Erde (ihre wärmende Seite) und nicht die wolkenbedingte Streuung und Reflektion des Sonnenlichtes. Wegen dieser einseitigen Einflussnahme der Treibhausgase sollte eine Neubewertung von Wolken erforderlich sein. Es ist zu vermuten, dass, im Gegensatz zur Lehrmeinung, jede Form von Wolken zur Erdkühlung beiträgt! Bisher galt, dass nur tiefe, optisch dichte Wolken die Erde kühlen, aber hohe, optisch dünne Wolken die Erde erwärmen (3).
Die gegenseitige Konkurrenz bedeutet, dass auch umgekehrt Wolken/Aerosole die Wirksamkeit der Treibhausgase verringern. Deswegen sind Zweifel an der IPCC-Formel für den CO2-Strahlungsantrieb angebracht (Gleichung 3), da hier nur die theoretische CO2-Strahlung ohne Hintergrundstrahlung berechnet wird. Eine ausführliche Auseinandersetzung mit dieser IPCC-Formel und Vorstellung einer eigenen CO2-Strahlungsformel soll in der nächsten Mitteilung erfolgen.
Gleichung 3:
Aus Abb. 1 ist auch ersichtlich, dass eine Messung der IR-Gas-Strahlung (mit dieser Apparatur) nur vor einem wesentlich kälteren Hintergrund möglich ist. Wenn Erd- und Aerosol-Platte die gleiche Temperatur haben ist die Strahlungskühlung PE null, unabhängig ob Treibhausgase vorhanden sind oder nicht.
Hinzukommt, dass Treibhausgase (bei bestimmten Wellenlängen) durchsichtig sind. Der IR-Sensor (die Erd-Platte) „sieht“ nicht nur die IR-Gase, sondern auch den Hintergrund (Aerosol-Platte). Beide Strahlungsquellen gehen also in die IR-Messung ein. Ideal wäre ein Hintergrund mit der Temperatur TH = 0, von dem keine IR-Strahlung ausgeht. Die hohe Linearität R2 (Pearson-Funktion > 0,998) der gefundenen Trendlinien PE (Tab. 1) bei der Abkühlung bis -18 °C macht es aber möglich, durch Extrapolation bis TH = 0 rechnen zu können. So lässt sich die reine IR-Gas-Strahlung (ihr theoretisches Strahlungspotential), ohne Hintergrundstrahlung der Aerosol-Platte, ermitteln.
Zusätzlich zur Strahlung der Aerosol-Platte gibt es noch eine Strahlung der Aluminiumwand der Apparatur, die als eine Konstante die Messungen beeinflusst und bei der Messung „ohne IR-Gas“ mit 102 W/m2 ermittelt wurde (1).
Die vorgestellten Versuche sind nur Labor-Untersuchungen, die den Treibhauseffekt der erdnahen Atmosphäre modellieren. Aber wird die IR-Gegenstrahlung der realen Atmosphäre auch von Wolken beeinflusst? Das ist eine Frage, die sich schon die Pioniere der Klimaforschung stellten. Schon Anfang des 20. Jahrhunderts hat Knut Ångström ein Pyrgeometer entwickelt, das die „dunkle“ (IR) Strahlung der Atmosphäre ermitteln konnte (4). Wie auch bei der eigenen Apparatur wurde der elektrische Strom gemessen, der für eine gleichbleibende Temperatur eines geschwärzten, dem Himmel ausgesetzten Thermoelementes benötigt wird. So gesehen ist die vorgestellte, eigene Apparatur eine Anlehnung an das Pyrgeometer von Knut Ångström. Sein Sohn, Anders Ångström, und Sten Asklöf haben die nächtliche „Wärmeaustrahlung“ in verschiedenen Regionen der Erde untersucht und festgestellt, dass sie von der Lufttemperatur und der Luftfeuchtigkeit aber vor allem vom Bewölkungsgrad abhängt (5). Es wurde gefunden, dass die effektive Ausstrahlung (Strahlungskühlung) der Erde bei bewölktem Himmel nur rund 23 % im Vergleich zum klaren Himmel beträgt. Diese ersten, einfachen Messungen der effektiven IR-Ausstrahlung der Erde wurden durch spätere Messungen mit verbesserten Geräten überprüft. Dabei wurde festgestellt: „Bei bedecktem Himmel betrug die Intensität der effektiven Ausstrahlung im Mittel 18,5% des Wertes bei wolkenlosem Himmel“ (6).
Dass Wolken als starke IR-Strahler die nächtliche Abkühlung (z.B. im Winter) erheblich mindern können, gehört mittlerweile zum Allgemeinwissen. Angesicht der vielen bekannten Untersuchungen wären eigene Messungen eigentlich nicht nötig gewesen. In der Zwischenzeit sind jedoch die Geräte zur Messung der IR-Strahlung dank Mikroelektronik nicht nur wesentlich handlicher, sondern vor allem auch erschwinglicher geworden. Um mit eigenen Augen die atmosphärische Gegenstrahlung kennenzulernen, wurde die IR-Strahlung des Himmels über Berlin von Juli 2016 bis Mai 2017 in unregelmäßigen Abständen mit einem Pyrometer PCE-891 (ein Infrarot-Thermometer) bei unterschiedlichen Bewölkungsgraden gemessen. Die Messungen des bewölkten Himmels zeigten erwartungsgemäß eine sehr starke, durch Wolken verursachte Gegenstrahlung. Unerwartet spannend wurden die Messungen des wolkenfreien Himmels. Nach Auffassung von F. Möller sind nur die IR-Gase Wasserdampf, CO2 und in kleinem Umfang Ozon, Methan und Lachgas die Ursache der atmosphärischen Gegenstrahlung bei klarem Himmel, die sich mit seinen Strahlungsdiagrammen berechnen lassen (7). Die IR-Strahlung von Wasserdampf und CO2 wird nicht bestritten. In den folgenden Kapiteln wird jedoch gezeigt, dass mit hoher Wahrscheinlichkeit auch von den nicht sichtbaren Aerosolen eine erhebliche IR-Strahlung erzeugt wird und hier ein Umdenken erforderlich ist.
Der wolkenfreie Himmel – die Strahlung der nicht sichtbaren Aerosole?
Laut Wikipedia sind die IR-aktiven Gase die einzigen IR-Strahler, die bei klarem Himmel eine Gegenstrahlung zur Erde schicken. „Bei klarem Himmel besteht die Gegenstrahlung hauptsächlich aus der Wärmestrahlung der Atmosphärengase“ (8).
So wurde mit einem Pyrgeometer (im IR-Wellenlängenbereich von 5 bis 25 μm) von einer Wetterstation bei München am 6. Oktober 2005 der Verlauf der Gegenstrahlung während eines Tages gemessen. „Während des Vormittags herrschte Hochnebel. Die Nebeltröpfchen trugen als effiziente langwellige Strahler zu relativ hohen Strahlungswerten von ca. 370 W/m² bei. Gegen Mittag löste sich der Nebel auf und ließ einen klaren Himmel zurück. Die Atmosphärengase alleine sind weniger effiziente langwellige Strahler, die Strahlungswerte gingen daher merklich zurück, auf etwa 300 W/m². … Über das Jahr und den ganzen Globus gemittelt beträgt die Intensität der Gegenstrahlung etwa 300 W/m² “.
Die These einer exklusiven IR-Gas-Strahlung deckt sich mit der Aussage neuzeitlicher Meteorologen: „Der klare Himmel enthält nur wenige kleinste Partikel. Es liegt eine reine gasförmige Atmosphäre und kein Aerosol vor…“ (9).
Die Thesen provozieren allerdings Zweifel, denn dann hätten die großen Ballungsgebiete der Erde kein Feinstaubproblem, es gäbe keinen Sahara-Staub, die Pflanzen kämen ohne Pollen aus und es wäre fraglich wie sich Wolken überhaupt bilden können, denn: „Die Wassertröpfchen (der Wolken) bilden sich um Kondensationskerne (Aerosole, Anm. d Verf.) herum, wenn die relative Feuchtigkeit der Luft 100 % geringfügig (um höchstens 1 %) übersteigt“ (10).
Tatsächlich gibt es eine Reihe von Beobachtungen und Indizien, die alle darauf hinweisen, dass die atmosphärische Gegenstrahlung bei wolkenfreien Himmel gemeinsam von IR-aktiven Gasen (hauptsächlich Wasserdampf und CO2) und den nicht sichtbaren Aerosolen erzeugt wird. Aufgeführt werden drei völlig unterschiedliche Untersuchungen: Die eigenen Temperatur-Messungen des klaren Himmels über Berlin (Kap. 2.1), Messungen der Boden-Temperatur aus größerer Höhe (Kap. 2.2) und Berechnungen der Wasserdampf-Strahlung mit Formel von Ångström und anderen Forschern (Kap. 2.3). Jedes dieser Argumente mag für sich alleine fragwürdig sein, aber in ihrer Summe bilden sie ein schlüssiges Konzept einer Aerosol-Strahlung, die von der modernen Klimaforschung offensichtlich vernachlässigt wurde. Dabei waren sich die Vorväter der Meteorologie ursprünglich einig, dass sich: „Millionen von Staubteilchen in der Luft befinden und sogar einen Beitrag zur sogenannten Rückkehr- oder Kältekonvektion während der nächtlichen Abkühlung leisten“ (11).
Temperatur-Messungen des wolkenfreien Himmels
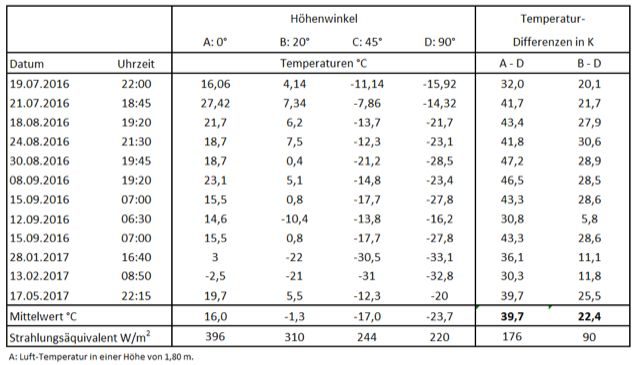
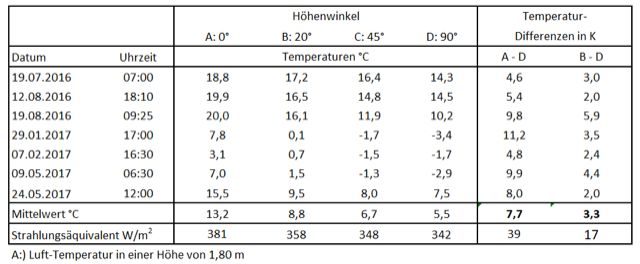
Zum Erforschung der atmosphärischen Strahlung wurde der wolkenfreie Himmel über Berlin zu unterschiedlichen Tag- und Nachtzeiten mit einem Pyrometer PCE-891 (ein Infrarot-Thermometer) gescannt. Das verwendete Pyrometer besitzt einen eingebauten Filter, der nur IR-Strahlen der Wellenlängen 8 – 14 µm durchlässt und ist mit einer Optik 50:1 ausgestattet, die eine Fokussierung ermöglicht. Damit misst das Pyrometer in einem Wellenlängenbereich, der nur wenig von CO2 oder Wasserdampf beeinflusst wird (atmosphärisches Fenster). Protokolliert wurde die Temperatur des Himmels bei Höhenwinkeln von 0 bis 90 Grad (Winkel über dem Horizont). Dabei wurde die Messung bei 0 Grad mit der Lufttemperatur in einer Höhe von 1,8 m gleichgesetzt. Die gefundenen Messwerte sind extrem vom Höhenwinkel abhängig (Tab. 2). Im Durchschnitt wurde ein Unterschied von 22 K zwischen den Winkelmessungen von 20 und 90 Grad gefunden. Die starke Winkelabhängigkeit lässt sich durch schwache IR-Strahler erklären, die eine große Schichtdicke (mehrere Kilometer) für die Sättigung ihrer Strahlungen benötigen. Dabei ist bei der senkrechten Messung der Anteil der kalten atmosphärischen Schichten größer als beim flachen 20 Grad Winkel. Um eine Vorstellung zu bekommen, was die Temperatur-Messungen bedeuten, wurde in der Tabelle ein „Strahlungsäquivalent“ in W/m2 angegeben. Es ist die Strahlungsdichte, die ein „Schwarz-Körper“ bei den gemessenen Temperaturen emittieren würde.
Wer oder was verursacht aber diese IR-Strahlungen? Der Messbereich des Pyrometers von 8 – 14 µm ist zu groß, um Treibhausgase per se auszuschließen zu können. Da wäre zunächst das Ozon, das bei 9,6 µm, also ziemlich mittig, ein Emissions-Maximum hat. Bei den Ozon-Emissionen handelt es sich um sehr kleine, selbst im Zentrum nicht gesättigte Banden, die vernachlässigt werden können. Aus den Messungen des Wettersatelliten Tiros im Wellenlängenbereich 7,5 – 13,5 µm weiß man, dass auch in geringem Umfange CO2 und Wasserdampf IR-Emissionen in diesem Wellenbereich aussenden (siehe Kap. 2.2). Diese beiden Treibhausgase können also teilweise die Winkelabhängigkeit erklären. Allerdings sind die beobachten Unterschiede der Himmels-Strahlung von 90 W/m2 zwischen der 20 und 90 Grad Messung (Tab. 2, B – D) zu hoch, um sie allein durch H2O- und CO2-Strahlung erklären zu können. Schließlich haben diese Gase im Wellenbereich des Pyrometers keinen Haupt-Peak sondern nur Ausläufer, die die Messung beeinflussen. So bleibt als plausible Erklärung nur die Annahme einer gemeinsamen Strahlung von Treibhausgase und Aerosolen. Aerosole, als feste oder flüssige Partikel, erzeugen eine kontinuierliche Strahlung mit einem Maximum zwischen 11 und 12 µm (Wiensches Verschiebungsgesetz), das perfekt mit dem Messbereich des Pyrometers übereinstimmt.
Tabelle 2: Temperaturmessung bei klarem Himmel: Pyrometer PCE-891
Die Winkelabhängigkeit der IR-Gegenstrahlung bei klarem Himmel ist keineswegs eine neue Entdeckung. So wurde bereits 1933 in der Nacht vom 19. zum 20. Mai in Föhren bei Trier mit einem „Effektiv-Aktinometer“ eine Abhängigkeit der effektiven Ausstrahlung (Strahlungskühlung) vom Höhenwinkel festgestellt (Tab. 3) (12).
Tabelle 3: „Meridionale Intensitätsverteilung der effektiven Ausstrahlung in relativen Einheiten, Zenit = 100“ nach Kessler und Kaempfert
 Temperaturmessung der Erdoberfläche aus größerer Höhe
Temperaturmessung der Erdoberfläche aus größerer Höhe
Im Juli 1961 wurde von der NASA der Wettersatellit TIROS III in eine Erdumlaufbahn gebracht, der u.a. mit einen IR-Sensor (Tiros Channel 2, IR-Empfindlichkeitsbereich von 7,5 – 13,5 µm) ausgerüstet war. Dabei stellte sich heraus, dass die im Orbit gemessenen Strahlungstemperaturen der Erdoberfläche stets niedriger sind als die tatsächlichen Temperaturen vor Ort. Es wurde erkannt, dass die Temperatur-Messungen von der (kalten) Atmosphäre beeinflusst wurden. Das „atmosphärische Fenster“ im Bereich 7,5 – 13,5 µm war offensichtlich nicht so transparent wie erhofft. Dabei wurden vor allem die IR-Strahlungen von Wasserdampf, CO2 und Ozon als Ursache dieser Atmosphären-Strahlung ausgemacht. Die nicht sichtbaren Aerosole als weitere Strahlungsquelle wurden merkwürdigerweise nicht beachtet. Dabei gab es einen deutlichen Hinweis auf eine mögliche Aerosol-Strahlung. So betrug die Abweichung 13,3 K bei einer „extrem feuchten“ Atmosphäre über Panama (15.11.1961). Über der trockenen Sahara- Wüste (Colomb-Bechar, 15.07.1961) betrug trotz geringer Wasser-Konzentration die Abweichung immer noch 8,8 K (13). Das ist ein Wert, der ausreichend Raum für eine Aerosol-Strahlung bietet.
Ein weiterer Hinweis findet sich im Bericht über Temperatur-Messungen von Wasseroberflächen aus einer Höhe von bis zu 2400 m (vom Flugzeug oder Hubschrauber) mit einem PRT-Radiometer im Spektralbereich 8 – 13 µm. Wie schon bei den Messungen des Tiros-Satelliten wurde eine Abweichung zwischen Strahlungs-Temperatur und tatsächlicher Oberflächen-Temperatur festgestellt. Wegen der geringeren Höhe war die Abweichung mit 2 – 3 K entsprechend kleiner. Dabei erwies sich der Einfluss der Luftfeuchte geringer als erwartet: „Die Erfahrung zeigt, dass die Luftfeuchtigkeit einen wesentlich geringeren Einfluss auf die Korrekturwerte für die Strahlungstemperatur hat als die Lufttemperatur“ (14). Auch wenn der Autor die Rolle der Aerosole nicht anspricht, können seine gefundenen Abweichungen als Aerosol-Strahlung interpretiert werden.
Die Wasserdampf-Strahlung bei wolkenfreiem Himmels
Die Messungen des wolkenfreien Himmels mit dem Ångström-Pyrgeometer zeigten, dass die atmosphärische Gegenstrahlung von Temperatur und Feuchtigkeit der Luft abhängig ist. Zur Berechnung dieser Strahlung ließ sich Ångström von der Überlegung leiten, dass die effektive IR-Ausstrahlung Ae der Erde durch die Differenz von ihrer Ausstrahlung (σ ∙ T4Erde) und der Gegenstrahlung der Atmosphäre (G) gebildet wird (Gleichung 4, siehe auch Gleichung 1) (5). Stellt man die Gleichung um, ist die Gegenstrahlung G die Differenz von Erd- und effektiver Ausstrahlung. Dabei wird nach Ångström die effektive Ausstrahlung Ae durch eine modifizierte Stefan-Boltzmann-Gleichung berechnet, deren Koeffizienten experimentell ermittelt wurden. Unter der Annahme, dass erdnahe Atmosphäre und Erdoberfläche die gleiche Temperatur haben lässt sich die Gegenstrahlung G nach Gleichung 4 berechnen.
Gleichung 4:

Umfangreiche Messungen in den nachfolgenden Jahren bestätigten, dass die Gegenstrahlung von Luft-Temperatur und -Feuchte abhängt. Dabei wurden die Koeffizienten von Bolz und Falkenberg korrigiert (15).
Gleichung 5:
![]()
In der Klimaforschung ist es heute üblich, Strahlungsdiagramme zur Berechnung der atmosphärischen Aus- und Gegenstrahlung auf Basis der Absorptionslinien der IR-aktiven Gase zu benutzen (7). Die Rechnungen benötigen Großrechner und sind für einen Außenstehenden schwer nachzuvollziehen und vor allem nicht überprüfbar. Da sie die Ergebnisse von Ångström aber im Grundsatz bestätigen, kann man weiterhin mit der einfachen bzw. korrigierten Ångström-Formel die Wasserdampf-Strahlung ermitteln. Vor allem sind die Rechnungen vertrauenswürdig, da sie von einer großen Zahl von Feldversuchen bestätigt wurden. Tab. 4 zeigt die atmosphärische Gegenstrahlung bei einer Lufttemperatur von 15 °C, berechnet nach der Formel von Bolz/Falkenberg für Luftfeuchten von 0 bis 100 % (Klammer-Werte wurden nach der Ångström-Formel berechnet). Der Anteil der Wasserdampf-Strahlung an der berechneten Gegenstrahlung wurde aus der Zunahme der IR-Strahlung zum Basiswert von 223 W/m2 (ohne Wasserdampf; rel. Feuchte = 0) ermittelt.
Die Rechnungen offenbaren zwei fundamentale Widersprüche: Die atmosphärische Gegenstrahlung wird bei klarem Himmel bei 15 °C nur zu einem kleinen Teil (30 % nach Bolz/Falkenberg) von Wasserdampf verursacht, und die H2O-Strahlung ist viel kleiner als nach den Absorptionsbanden des Wasserdampfes zu erwarten wäre.
Tabelle 4: Berechnungen der atmosphärischen Gegenstrahlung bei wolkenfreiem Himmel bei 15 °C nach Bolz/Falkenberg und Ångström (in Klammern)
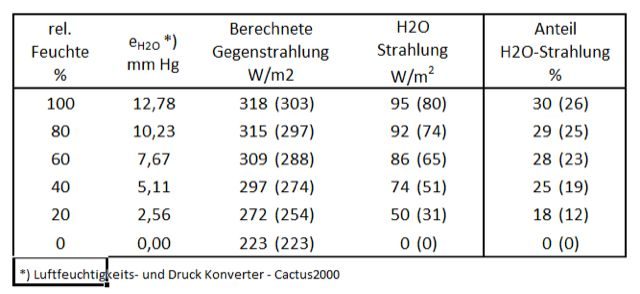
Die o.g. These: „Bei klarem Himmel besteht die Gegenstrahlung hauptsächlich aus der Wärmestrahlung der Atmosphärengase“ wird durch diese Rechnungen nicht bestätigt. Addiert man zur Wasserdampf-Strahlung noch die CO2-Strahlung (angeblich rund die Hälfte der H2O-Strahlung) kommen die beiden wichtigsten Treibhausgase nur auf rund 45 % der atmosphärischen Gegenstrahlung. 55 % der atmosphärischen Gegenstrahlung werden also nicht von Treibhausgasen erzeugt! Es muss noch eine weitere Strahlungsquelle (die Strahlung der Aerosole?) geben, um die gemessene Gegenstrahlung des Himmels erklären zu können.
Aber auch die maximal erreichbare H2O-Strahlung von 95 W/m2 bei 100 % rel. Feuchte ist verwunderlich. Dieser Wert ist nur 50 % der theoretischen H2O-Strahlung von rund 190 W/m2. Letzteres ist ein Schätzwert, der sich aus dem Planck’schen Strahlungsgesetz und der Annahme der Sättigung aller H2O-typischen Absorptionsbanden zwischen 5 – 8 und 17 – 100 µm bei 15 °C ergibt.
Diese Widersprüche lassen sich durch eine gemeinsame Gegenstrahlung von Wasserdampf und Aerosolen auflösen, worauf in Kap. 3 ausführlicher eingegangen wird.
Anmerkung: Das Pyrgeometer von Ångström hat keinen Strahlungs-Filter. Es werden alle relevanten Wellenlängen der atmosphärischen Gegenstrahlung erfasst. Damit wird hier, anders als bei den eigenen Messungen (Kap. 2.1), die gesamte atmosphärische Gegenstrahlung gemessen.
Die IR-Gegenstrahlung unter Wolken
1. Temperatur-Messungen des bedeckten Himmels
Nach der gleichen Methode, wie im Kap. Der wolkenfreie Himmel – die Strahlung der nicht sichtbaren Aerosole?.1 beschrieben, wurde der wolkenbedeckte Himmel (tiefe Schichtwolken) über Berlin mit dem Pyrometer PCE-891 gescannt (Tab. 5).
Wie schon bei der Temperatur-Messung bei klarem Himmel dargelegt, erfassen die Messungen nur einen Teil der atmosphärischen Gegenstrahlung (Wellenlängen-Bereich von 8 – 14 µm). Die starke Zunahme der IR-Strahlung von 122 W/m2 (90 Grad Messungen), im Vergleich zum wolkenlosen Himmel (Tab. 2 und Tab. 5), zeigt eindeutig, dass hier hauptsächlich die Strahlung der Wolken gemessen wird.
Ansonsten zeichnet sich diese Messreihe unter Wolken durch eine geringere Winkelabhängigkeit der Messwerte von 3,3 K zwischen der 20 und 90 Grad Messung aus, die sich aus dem relativ kurzen Abstand von Boden und Wolken ergibt. Damit bestätigt sich die These, dass die Winkelabhängigkeit der Temperatur-Messungen von schwachen Strahlern der Atmosphäre verursacht wird, die mehrere Kilometer Atmosphäre für eine gesättigte Strahlung benötigen, die unter Wolken nur bedingt vorhanden ist.
Tabelle 5: Temperaturmessung des bedeckten Himmels: Pyrometer PCE-891
 2. Die Wasserdampf-Strahlung bei bedecktem Himmel
2. Die Wasserdampf-Strahlung bei bedecktem Himmel
Übereinstimmend fanden Ångström und Asklöf, dass die effektive Ausstrahlung AW der Erde in Gegenwart von Wolken je nach Wolkenbedeckungsgrad und ihrer Höhe erheblich verringert wird. Aw wird aus der effektiven Ausstrahlung A0 (klarer Himmel) durch Multiplikation mit den Koeffizienten k und w erhalten (5).
Gleichung 6:
![]()
Die Gegenstrahlung für den vollständig bedeckten Himmel (w = 10) und einer durchschnittlichen Wolkenhöhe (k = 0,765) ergibt sich nach Gleichung 7, wobei für A0 der Ausdruck Ae aus Gleichung 4 eingesetzt wird.
Gleichung 7:
![]()
Tab. 6 zeigt die atmosphärische Gegenstrahlung bei vollständiger Wolkenbedeckung und einer Lufttemperatur von 15 °C bei rel. Luftfeuchten von 0 bis 100 %. Der Anteil der Wasserdampf-Strahlung an der berechneten Gegenstrahlung wurde aus der Zunahme der IR-Strahlung zum Basiswert von 351 W/m2 (ohne Wasserdampf; rel. Feuchte = 0) ermittelt.
Tabelle 6: Berechnungen der atmosphärischen Gegenstrahlung bei vollständiger Wolkenbedeckung und 15 °C nach Ångström/Asklöf
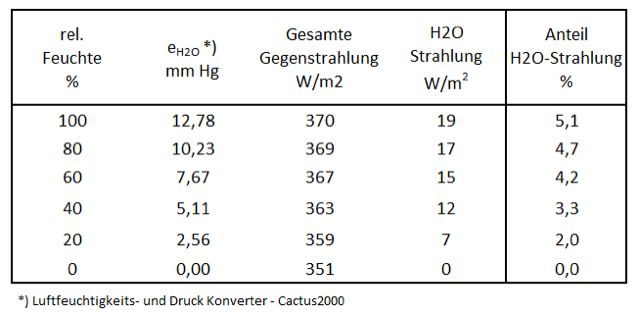 Als erstes fällt die geringe Auswirkung der Luftfeuchte auf. Selbst bei 100 % rel. Luftfeuchtigkeit beträgt der Anteil der Wasserdampf-Strahlung nur 5 % (19 W/m2) der berechneten Gegenstrahlung von 370 W/m2.
Als erstes fällt die geringe Auswirkung der Luftfeuchte auf. Selbst bei 100 % rel. Luftfeuchtigkeit beträgt der Anteil der Wasserdampf-Strahlung nur 5 % (19 W/m2) der berechneten Gegenstrahlung von 370 W/m2.
Wegen der geringen Wirkung des Wasserdampfes wurden von anderen Forschern alternative Formeln vorgeschlagen, die den Wasserdampf ganz weglassen („da er in der Messgenauigkeit untergeht“) und nur die Wolkenbedeckung als Parameter berücksichtigen (15).
Zur Erinnerung, die Gegenstrahlung (erdnaher Treibhauseffekt) wirkt sich nach Gleichung 1 unmittelbar und direkt auf die Kühlung (Strahlungskühlung) der Erde aus. Die Erde kann bei 15 °C (100 % Feuchte) nur 21 W/m2 (391 – 370) durch IR-Strahlung loswerden. Kein Wunder, dass die Temperaturen bei einer nächtlichen Abkühlung unter einer geschlossenen Wolkendecke kaum zurückgehen. Aber der entscheidende Punkt ist, dass Wasserdampf an diesem starken Effekt nur zu 5 % beteiligt ist. Diese Erkenntnis ist angesichts der aktuellen Global-Warming-Diskussion von besonderer Tragweite. Wasserdampf ist kein x-beliebiges Treibhausgas, sondern das wirksamste IR-aktive Gas der Atmosphäre, das angeblich für 66 bis 85 % aller absorbierten IR-Strahlungen verantwortlich sein soll (16).
Die Naturbeobachtungen (Formeln) der frühen Forscher bestätigen im vollen Umfang die eigenen Laborversuche und daraus abgeleiteten Schlussfolgerungen. Danach verlieren die Treibhausgase in Gegenwart einer geschlossenen Wolkendecke fast vollständig ihre Wirksamkeit.
Selbst moderne IR-spektroskopische Messungen der atmosphärischen Gegenstrahlung in Barrow (Alaska) zeigen, dass der erdnahe Treibhauseffekt der IR-aktiven Gase unter Wolken völlig verschwinden kann (17).
Auch ein Vergleich der beiden Strahlungs-Rechnungen (Tab. 4 und Tab. 6) für den klaren und bewölkten Himmel bietet einige interessante Aspekte:
Ohne Wasserdampf (rel. Feuchte = 0) verursachen Wolken eine Zunahme der Gegenstrahlung von 128 W/m2 (351 vs. 223 W/m2). Ein vergleichbarer Wert von 122 W/m2 wurde bei den eigenen Temperatur-Messungen, allerdings im Messbereich 8 – 14 µm, gefunden (Kap. 3.1).
Aber in einer feuchten Atmosphäre (100 % rel. Feuchte) ist der wolkenbedingte Zuwachs nur noch 67 W/m2 (auf Basis der Ångström-Werte 370 vs. 303 W/m2) (Tab. 4 vs. Tab. 6).
Diese Betrachtungen sind ein weiterer Beweis, dass bei einer gemeinsamen Strahlung von Treibhausgasen und Wolken beide Strahlungsquellen ihre Wirksamkeit einbüßen. Die im Labor gefundenen Zusammenhänge sind also keinesfalls neu, sondern weisen nur experimentell nach, was ursprünglich Lehrmeinung und festes Wissen von Meteorologen und Klimaforschern war.
Die moderne Klimatologie hat die früheren Bestimmungen der erdnahen Gegenstrahlung durch spektroskopische Messungen der IR-Ausstrahlung (Transmission) am oberen Rand der Atmosphäre TOA (Top of the Atmosphere) aus Sicht von Wetter-Satelliten (z.B. Nimbus 4) ersetzt. Die TOA-Spektren zeigen auffällige Absorptions-Kegel für Ozon aber vor allem für CO2, die zu einer Verringerung der gesamten Transmission beitragen. Es wird geschlussfolgert, dass sich die Erde erwärmen muss, um mit den anderen Wellenlängen die fehlenden Transmissionen auszugleichen. Diese Interpretation setzt voraus, dass sich zwischen TOA und Erdoberfläche keine weiteren Strahler befinden. Akzeptiert man aber die Existenz der Aerosole und Wolken als weitere Strahler der Atmosphäre lässt sich schlussfolgern, dass nicht unmittelbar die Erdoberfläche, sondern die Aerosole und die Oberseiten der Wolken sich etwas erwärmen. Ein Vorgang, der indirekt auch die Temperatur der Erdoberfläche beeinflussen sollte, allerdings wesentlich abgeschwächter als die unmittelbar wirksame IR-Gegenstrahlung des erdnahen Treibhauseffektes.

Abb. 2: Berlin am 14.06.2017, 12:20 Uhr, Luft: 20,0 °C (1,8 m): Temperatur-Messungen unterschiedlich dichter Wolken und wolkenfreier Abschnitte.
Die IR-Strahlungen der Wolken und Aerosole sind ähnliche Strahlungskomponenten der Atmosphäre mit kontinuierlichen Übergängen. Aerosole und Wassertropfen zeichnen sich durch eine sehr große Oberfläche (bezüglich ihrer Masse) aus. Das ist eine wichtige Voraussetzung einer Oberflächen-Strahlung von festen und flüssigen Stoffen. In der Atmosphäre ist diese Partikel-Strahlung von ihrer Konzentration (Partikel pro m3 Luft) und der Temperatur ihrer Umgebung abhängig, wie in Abb. 2 deutlich zu sehen ist.
Anhang- Experimentelle Daten
QE ist die elektrische Heizung einer fiktiven Erd-Platte mit einer Fläche von 1 m2. Die tatsächlich gemessenen Werte der verwendeten Erd-Platte (219,04 cm2) sind um den Faktor 0,0219 kleiner. UH ist die Spannung von 5 in Reihe geschalteten Peltier-Elementen (TEC1-12706) auf der Aerosol-Platte, die mit dem Voltmeter (Voltacraft VC 250) gemessen wurden. Diese Elemente registrieren die IR-Ausstrahlung (Strahlungen der Erd-Platte, der Seitenwand und der IR-Gase) und die Wärmeleitung der unmittelbaren Umgebung. Da die Wärmeleitung beim Abkühlen der Aerosol-Platte ständig zunimmt, wird UH bei Experimenten im Abkühlungs-Modus nicht ausgewertet, sondern nur zur Information in den folgenden Tabellen angegeben.
Tabelle 7: ohne IR-Gase
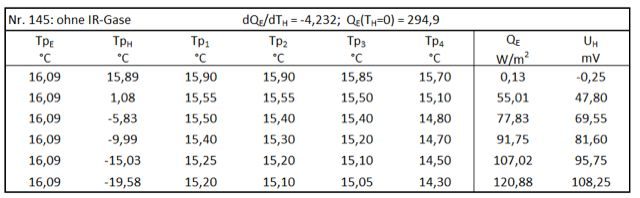
Tabelle 8: Methan
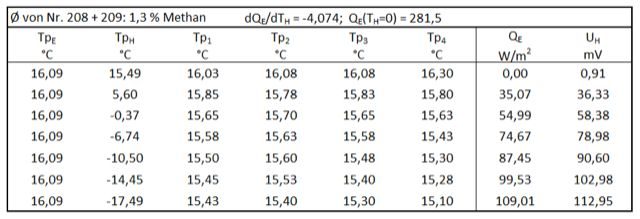
Tabelle 9: CO2
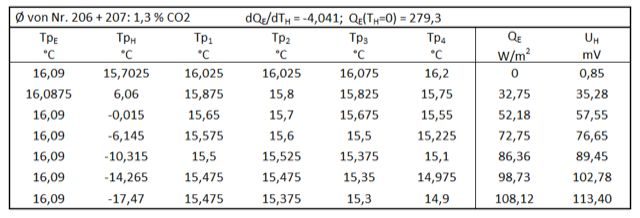
Tabelle 10: Lachgas
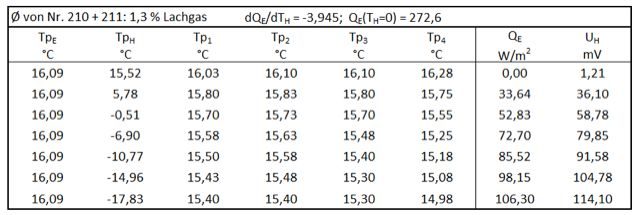
Tabelle 11: Propan
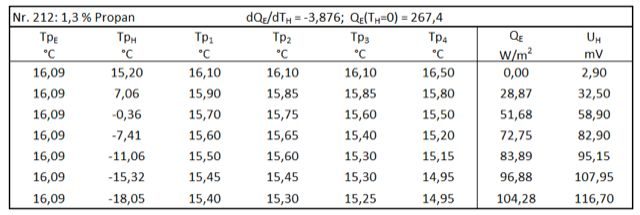
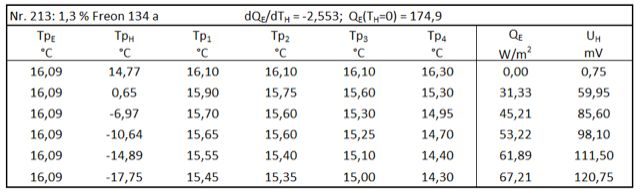
Tabelle 12: Freon 134a
Literaturverzeichnis
1. Schnell, Michael. Experimentelle Verifikation des Treibhauseffektes Teil 1: Die gegenseitige Beeinflussung von Wolken und Treibhausgasen. [Online] 25. März 2018. https://www.eike-klima-energie.eu/2018/03/25/experimentelle-verifikation-des-treibhauseffektes-teil-1-die-gegenseitige-beeinflussung-von-wolken-und-treibhausgasen/.
2. Schönwiese, Christian-Dietrich. Klimatologie. Stuttgart : Eugen Ulmer GmbH, 1994.
3. Wagner, Thomas. Strahlungsprozesse in der Atmosphäre. [Online] [Zitat vom: 28. Mai 2018.] https://www.mpic.de/fileadmin/user_upload/pdf/Physik_der_Atmosphaere_Lecture_Wagner.pdf.
4. Michael Krueger. Das Pyrgeometer von Knut Angström und die Bestimmung der Gegenstrahlung des atmosphärischen „Treibhauseffekts. [Online] 8. Oktober 2014. http://www.science-skeptical.de/blog/das-pyrgeometer-von-knut-angstroem-und-die-bestimmung-der-gegenstrahlung-des-atmosphaerischen-treibhauseffekts/0012776/.
5. Albrecht, Fritz. Untersuchungen über den Wärmehaushalt der Erdoberßäche in verschiedenen Klimagebieten. Reichsamt für Wetterdient. Berlin : Julius Springer, 1940.
6. F. Sauberer. Registrierungen der nächtlichen Ausstrahlung. Archiv für Meteorologie, Geophysik und Bioklimatologie, Serie B. 1951, Bde. Vol. 2, Seiten 347-359.
7. Möller, Fritz. Einführung in die Meteorologie. Mannheim/Wien/Zürich : Bibliographisches Institut, 1973. Bd. II.
8. Atmosphärische Gegenstrahlung. [Online] 17. April 2017. [Zitat vom: 1. Mai 2017.] https://de.wikipedia.org/.
9. Ewald Zmarsly, Wilhelm Kuttler, Hermann Pethe. Meteorologisch-klimatologisches Grundwissen: Eine Einführung mit Übungen, Aufgaben und Lösungen. Stuttgart : Eugen Ulmer GmbH & Co., 2002. S. 142.
10. Wolke. [Online] 13. Januar 2006. [Zitat vom: 01. Mai 2018.] https://de.wikipedia.org/wiki/Wolke.
11. Geiger, Rudolf. Das Klima der bodennahen Luftschicht. Braunschweig : Friedr. Vieweg & Sohn, 1942. S. 64.
12. Otto Wilhelm Kessler, Wolfgang Kaempfert. Die Frostschadenverhütung. Berlin Heidelberg : Springer-Verlag, 1940. S. 37.
13. Lönnqvist, Olov. A window radiation chart for estimating surface temperature from satellite observations. [Online] 19. Oktober 1963. https://www.tandfonline.com/doi/pdf/10.3402/tellusa.v15i4.8856.
14. LORENZ, DIETER. Der Einflus einer Luftzwischenschicht auf meteorologische 0berflächentemperaturmessungen mit Radiometern. [Online] 22. Januar 1968. https://onlinelibrary.wiley.com/doi/pdf/10.1111/j.2153-3490.1969.tb00419.x.
15. Schulze, Rudolf. Strahlenklima der Erde. Darmstadt : Dr. Dietrich Steinkopff, 1970. S. 103. Bd. 72.
16. Winter, Maiken. Welche Rolle hat der Wasserdampf beim Treibhauseffekt? [Online] 01. Januar 2008. [Zitat vom: 24. Mai 2018.] https://www.cleanenergy-project.de/gesellschaft/green-lifestyle/wasserdampf-treibende-kraft-beim-treibhauseffekt/.
17. Christopher J. Cox, Penny M. Rowe, Steven P. Neshyba, and Von P. Walden. A synthetic data set of high-spectral-resolution infrared spectra for the Arctic atmosphere. [Online] Earth Syst. Sci. Data, 8, 199–211, 2016, 18. 01 2016. [Zitat vom: 23. 01 2018.] https://www.earth-syst-sci-data.net/8/199/2016/essd-8-199-2016.pdf.
Hier die englische Version des Beitrages 2. Communication – Experimental verification of the greenhouse effect