Fangen wir mit dem Stefan-Boltzmann-Gesetz noch einmal ganz von vorne an

Das Gleichheitszeichen im S-B Gesetz stellt nun aber die physikalische Bedingung „gleichzeitig in einem thermischen Gleichgewicht“ dar und keineswegs eine mathematische Rechenanweisung, Zitat aus dem Handbook of Chemistry and Physics [1], 55^thEdition 1974-1975, CRC Press 1974, Seite F-110:

„Stefan-Boltzmann law of radiation – The energy radiated in unit time by a black body is given by, E=K(T⁴-T₀⁴), where T is the absolute temperature of the body, T₀the absolute temperature of the surroundings, and K is a constant.”

Das Stefan-Boltzmann-Gesetz bezieht sich also auf die Betrachtung eines einzelnen Schwarzen Körpers mit einer definierten Temperatur, aus der sich unmittelbar zum Betrachtungszeitpunkt dessen aktuelle Strahlungsleistung gegenüber der Umgebung ableitet. Das Stefan-Boltzmann-Gesetz ist also keine mathematische Rechenanweisung zur Umrechnung von räumlich und zeitlich beliebig ermittelter durchschnittlicher Temperaturwerte in durchschnittliche Strahlungswerte oder umgekehrt. Vielmehr verbindet es ausschließlich gleichzeitige Individualwerte von Strahlung und Temperatur eines ganz konkreten einheitlichen Schwarzen Körpers. Das Stefan-Boltzmann-Gesetz bildet also eine unmittelbar zeitgleiche physikalische Beziehung ab und darf mithin keinesfalls zur mathematischen Umrechnung von irgendwelchen zeitlich und/oder räumlich zusammengefassten Durchschnittswerten benutzt werden – wie das leider trotzdem immer wieder geschieht.
Wenn wir auf unserer Erde über Temperaturentwicklungen reden, dann beziehen wir uns aber gemeinhin genau auf solche Durchschnittswerte. Für die Zeit vor den ersten Thermometermessungen stehen uns nämlich nur sogenannte Temperaturproxys zur Verfügung, um die Paläotemperaturen unserer Erde für frühere Zeiträume abzuschätzen. Unter dem Begriff Temperaturproxy werden natürliche Abfolgen zusammengefasst, die über ihren jahreszyklischen Aufbau Informationen über diejenige Temperatur enthalten, bei der sie entstanden sind. Das bekannteste Beispiel sind Baumringe, es können aber auch Tropfsteine, Korallen, Sedimentabfolgen oder Eisbohrkerne sein.  All diesen Temperaturproxys ist gemeinsam, dass sich daraus meist nur durchschnittliche Jahreswerte ableiten lassen, die üblicherweise auch noch eine jahreszeitlich oder regional begrenzte Aussagekraft besitzen. Und es gibt Klimaphänomene, die sich dort ebenfalls abbilden, mit der Temperatur aber gar nichts zu tun haben und daher zu fehlerhaften Aussagen führen können, beispielsweise wirkt Trockenheit auf Baumringe ähnlich wie niedrige Temperatur.
Dem Paläoklima unserer Erde können wir uns also bestenfalls über Durchschnittswerte der Temperatur nähern, weil es für die geologische Vergangenheit eben nichts anderes gibt. Daher erhält auch die ominöse „gemessene“ globale Durchschnittstemperatur ein gewisses Gewicht. Diese Durchschnittstemperatur wird zwar an vielen Stellen erwähnt, aber wenn man dann versucht in die Tiefe zu gehen, werden üblicherweise irgendwelche Scheinbezüge hergestellt. Selbst wenn dort konkret zugrunde liegende Datensätze genannt werden, fehlt der eindeutige Hinweis auf das statistische „Kochrezept“, das auf diesen Datensatz angewendet worden sein soll, um zu dem genannten Ergebnis zu kommen. Die „gemessene“ globale Durchschnittstemperatur erweist sich damit als höchst spekulativ und wissenschaftlich nicht nachvollziehbar. Der Deutsche Wetterdienstbeschreibt die globale Durchschnittstemperatur folgendermaßen, Zitat:

„Unter der globalen Durchschnittstemperatur versteht man die über die gesamte Erdoberfläche (Land/Wasser) gemittelte Temperatur in einem bestimmten Zeitraum. Da klimatologische Messungen über längere Zeiträume nur punktuell vorliegen, lassen sich Zeitreihen der globalen Mitteltemperatur nur annähernd bestimmen…

Die Angabe einer globalen Durchschnittstemperatur ist allerdings mit noch größeren Unsicherheiten behaftet als die Angabe von Abweichungen, da eigentlich kleinräumige Besonderheiten berücksichtigt werden müssten, während die Abweichungen räumlich einheitlicher sind. Daher werden bei den Zeitreihen meist nur die Abweichungen und nicht deren Absolutwerte angegeben.“
Diese Beschreibung geht nun also noch einen Schritt weiter, indem sie den Absolutbetrag der „gemessenen“ globalen Durchschnittstemperatur entwertet und irgendwelchen rechnerischen Differenzen eine geringere Unsicherheit zumisst. Das allerdings ist ganz große Zauberei, denn jede berechnete Differenz zu einem ungenauen Durchschnittswert ist natürlich vollautomatisch mit dessen Ungenauigkeit behaftet. Selbst bei der Beschränkung auf regionale Durchschnittswerte würde  bei kleinen Differenzen die relative Unsicherheit der Aussage ansteigen, beispielsweise ergibt sich allein bei einer Ungenauigkeit eines absoluten Messwertes von +/-0,5°C bereits eine Unsicherheit von +/-50% für einen auf dessen Basis ermittelten Differenzwert von 1,0°C.
Aber wie dem auch sei, es könnte tatsächlich eine gemessene globale Durchschnittstemperatur geben, wenn es ein ausreichendes globales Netz von ortsfesten primären Meßstationen geben würde, wenn von allen diesen Stationen eine ausreichend lange Zeitreihe vorliegen würde, wenn es ein wissenschaftlich abgestimmtes „Kochrezept“ für die statistische Berechnung gäbe, und wenn… wenn… wenn… Die Problematik solcher Temperaturmessreihen wird hierausführlich untersucht.
Und jetzt nehmen wir einfach einmal an, es gäbe eine solche gemessene globale Durchschnittstemperatur wirklich. Und daher lassen wir hier einfach einmal den vorgeblichen Wert von 14,8 °C für die gemessene globale Durchschnittstemperatur (NST) stehen, denn dieser Zahlenwert selbst hat auf die nachfolgende Betrachtung keinerlei Einfluss.
Schauen wir uns jetzt einmal an, was wir tatsächlich über den Klimamotor unserer Erde wissen:

• Die Einstrahlung der Sonne erfolgt mit durchschnittlich 940 W/m² temperaturwirksamer Strahlung auf einer Kreisfläche mit dem Erdradius und beleuchtet die Tagseite der Erde.
• Die Abstrahlung der Erdeerfolgt mit durchschnittlich 235 W/m² über ihre Gesamtfläche.
• Die „gemessene Durchschnittstemperatur der Erde“(NST) soll im langjährigen Mittel 14,8 °C betragen.
• Das Stefan-Boltzmann-Gesetzverknüpft Strahlung und Temperatur eines Schwarzen Strahlers im thermischen Gleichgewicht:
• P / A = s_*T⁴    mit  der Stefan-Boltzmann-Konstante  s= 5,670 10 ^-8[W m^-2K^-4]
• und P = Strahlung [W], A = Fläche [m²], T = Temperatur [°K]

Anmerkung:Die hier dargestellte S-B Fassung repräsentiert den vereinfachten Fall (T₀=0°K) des unter [1] beschriebenen vollständigen S-B Gesetzes, das in seiner ausführlichen Form auch als S-B Umgebungsgleichung bezeichnet wird.             
Und was fangen wir jetzt mit diesen Aussagen an?
Wir können die oben genannten Strahlungs-/ Temperaturwerte direkt miteinander in Beziehung setzen oder versuchen, ihnen mit dem Stefan-Boltzmann-Gesetz ihre jeweiligen S-B Äquivalente zuweisen:

1. 940 W/m² @ Kreisfläche =  235 W/m² @ Kugelfläche      Globale Energiebilanz
2. 235 W/m²~  -18 °C                          vorgeblich „natürliche“ S-B Temperatur der Erde (*)
3. (940/2=)470 W/m² ~ +28,6 °C     rechnerische S-B Temperatur der Tagseite (*)
4. 14,8 °C  ~  390 W/m²                       S-B Strahlungsäquivalent der Durchschnittstemperatur (*) 

Ergebnis: Alle mit (*) gekennzeichneten Aussagen verletzen das Stefan-Boltzmann-Gesetz!
Das S-B Gesetz beschreibt nämlich eine physikalisch eindeutige Verknüpfung von gleichzeitigen Werten von Strahlung und Temperatur für einen konkreten Schwarzen Körper. Wegen der diesem S-B Gesetz zugrunde liegenden T⁴-Beziehung lässt es keine mathematische Umrechnung von irgendwelchen durchschnittlichen Strahlungs- oder Temperaturwerten auf ein entsprechendes S-B Durchschnittsäquivalent zu. Daher muss beispielsweise eine Durchschnittstemperatur aus der Summe der beteiligten individuellen Ortstemperaturen ermittelt werden und nicht etwa aus dem Durchschnitt der individuellen örtlichen Strahlungswerte.
 (1) RICHTIG:Das wäre, unter der Voraussetzung einer langjährig konstanten gemessenen Durchschnittstemperatur, die durchschnittliche Energiebilanz unserer Erde. Der tatsächliche Ausgleich zwischen Ein- und Abstrahlung findet dabei über den gespeicherten Wärmeinhalt von Atmosphäre und Ozeanen statt. Dadurch ergibt sich bei der Abstrahlung eine permanente Zeitverzögerung über den Tages- und Jahresverlauf. Die aktuelle Sonneneinstrahlung wird also durch die Abstrahlung von Wärmeinhalten ausgeglichen, die teilweise schon längere Zeit von den globalen Zirkulationen verfrachtet worden waren. Aber insgesamt ist diese langjährige durchschnittliche Energiebilanz korrekt, solange die gemessene Durchschnittstemperatur tatsächlich konstant bleibt.
(2) FALSCH:Diese Berechnung ist falsch, weil sie die Gleichgewichtsbedingung des S-B Gesetzes missachtet und über eine Durchschnittsbildung mit der Nachseite der Erde die temperaturwirksame Sonneneinstrahlung willkürlich halbiert. Es wird üblicherweise versucht, diesen Ansatz dadurch zu retten, dass man dessen Differenz zur gemessenen Durchschnittstemperatur durch einen „natürlichen“ atmosphärischen Treibhauseffekt von 155 W/m² zu erklären sucht, für den es aber keinerlei wissenschaftlichen Nachweis gibt.
(3) FALSCH:Eine hemisphärische Betrachtung der globalen Temperaturgenese wäre eigentlich der richtige Ansatz. In dieser stark vereinfachten Form mit einer hemisphärischen Durchschnittsbildung widerspricht er jedoch dem Stefan-Boltzmann-Gesetz. Wenn man’s aber korrekt zu Ende denkt, landet man schließlich bei meinem hemisphärischen S-B Ansatz ohne Treibhauseffekt…
(4) FALSCH:Es gibt gar keine mittlere globale Abstrahlung von 390 W/m². Nur eine individuell gemessene Ortstemperatur von 14,8 °C hätte nach dem S-B Gesetz ein Strahlungsäquivalent von 390 W/m². Da sich die NST von 14,8 °C  aber aus der statistischen Bearbeitung von individuell gemessenen Ortstemperaturen zusammensetzt, müsste hier eine ebensolche statistische Mittelung über die jeweiligen örtlichen S-B Strahlungsäquivalente erfolgen. In der nachstehende Abbildung wird die globale Durchschnittstemperatur als ein Mittel aus +14,8°C +/- 35 °C betrachtet. Dabei stellen wir fest, dass sich die zugehörigen S-B Strahlungsäquivalente nicht proportional zu den Temperaturänderungen verhalten:

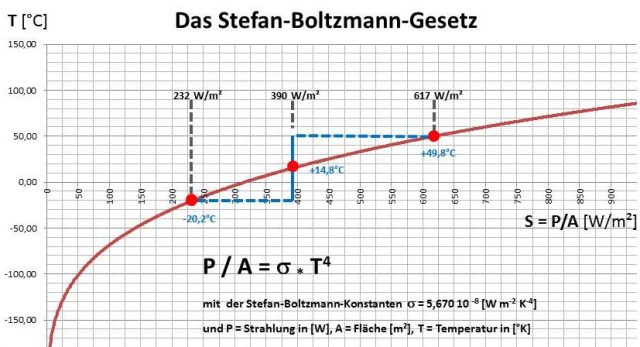
Wie bei einem T⁴-Gesetz zu erwarten ist, erhöht sich das individuelle S-B Strahlungsäquivalent mit ansteigenden Temperaturen überproportional. Wir erhalten für die ausgewählten Temperaturen damit folgende S-B Strahlungsäquivalente:

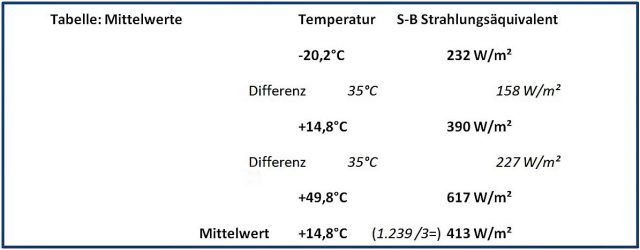
Eine beliebige symmetrische Temperaturverteilung um einen globalen Mittelwert von 14,8°C kann also niemals ein S-B Strahlungsäquivalent von 390 W/m² ergeben. Daher kann aus einem solchen falsch berechneten S-B Strahlungsäquivalent übrigens auch kein „natürlicher“ atmosphärischer Treibhauseffekt von 155 W/m² abgeleitet werden. Die hier vorgestellte einfache lineare Abschätzung aus 3 Einzelwerten liefert vielmehr rechnerisch einen „natürlichen“ Treibhauseffekt von

(413W/m²-235W/m²=) 178 W/m² anstelle der üblicherweise behaupteten 155 W/m²

und führt schon damit zu einem Widerspruch. Der „natürliche“ atmosphärische Treibhauseffekt resultiert also aus einer mangelhaften Kenntnis des Stefan-Boltzmann-Gesetzes, Zitat aus [1] zum ganz langsamen Mitdenken: „…energy radiated in unit time by a black body…where T is the absolute temperature of the body…“. Das Stefan-Boltzmann-Gesetz ist demnach nur unmittelbar „just in time“ gültig, es dürfen damit also weder zeitlich noch räumlich zusammenfassende Durchschnittswerte verknüpft werden.
ABER:Die NST selbst stellt eine langjährige globale Durchschnittstemperatur dar, bei der im Idealfall alle Energieflüsse (IN and OUT) über den Tag- und Nachtverlauf sowie die Breitenverteilung und der Jahresverlauf aller benutzten Meßstationen bereits korrekt herausgemittelt worden sein sollten. Dieser quasi-konstante NST-Wert ist damit um die langjährige Ein-und Abstrahlung bereinigt worden und hat überhaupt nichts mehr mit der globalen Strahlungsbilanz zu tun.Ihr tatsächlicher Wert spielt bei dieser Betrachtung also keine Rolle, und sein S-B Strahlungsäquivalent ist irrelevant.
Für den Fall, dass wir alle wetterabhängigen sowie tages- und jahreszeitlich variablen Prozesse auf unserer Erde in einer langjährigen Betrachtung als durchschnittlich ausgeglichen voraussetzen können, wie das bei einer konstanten NST ja der Fall sein sollte, lässt sich aus der richtigen Beziehung (1) und dem „ABER“-Kommentar zu (4) schließlich eine konkrete Aussage herleiten.
Die Gleichung für die globale Energiebilanz unserer Erde heißt damit:
(IN =940 W/m² _*pR²)  =  (OUT = 235 W/m² _*4 pR²)  @  NST (= 14,8 °C)
Wir haben hier auf unserer Erde also eine ausgeglichene globale Strahlungsbilanz bei einer konstanten global gemessenen Durchschnittstemperatur, wie immer diese auch ermittelt worden sein mag oder vielleicht erst viel später einmal korrekt ermittelt werden wird. Diese global gemessene Durchschnittstemperatur repräsentiert damit den durchschnittlichen globalen Netto-Wärmeinhalt von Atmosphäre und Ozeanen auf unserer Erde, um den herum permanent die hemisphärische Einstrahlung und die globale Abstrahlung erfolgen.