Signalanalyse – Randbedingungen für die Klimaforschung

Obere Grenzfrequenz

Die obere Grenzfrequenz – auch Nyquist-Frequenz genannt – ist in der Messtechnik wohlbekannt und besagt, dass ein analoges Signal mit der höchsten enthaltenen Frequenz f_max nur dann digital rekonstruiert werden kann, wenn es mit einer Frequenz größer als 2*f_maxabgetastet wurde.
Ein Sinussignal der Frequenz 50 Hz kann also nur dann nachgewiesen werden, wenn es mit mehr als 100 Hz abgetastet wird.
Umgekehrt gilt: Ein Signal der (Perioden-)Dauer x kann nur dann nachgewiesen werden, wenn die Messreihe eine zeitliche Auflösung von besser als x/2 hat. Für den Nachweis eines Sinussignals der Frequenz 50 Hz (d.h. der Periodendauer 0,02 s) muss die Abtastschrittweite kürzer als 0,01 s sein. Angewendet auf Zeiträume, die für die Klimaforschung wichtig sind: Um eine Variation von Größen wie Temperatur oder Meeresspiegel über einen Zeitraum von beispielsweise 30 Jahren zu erfassen, müssen Messreihen eine zeitliche Auflösung von weniger als 15 Jahren aufweisen.
Ist die zeitliche Auflösung (also die Abtastschrittweite) einer Messreihe schlechter als die halbe Dauer eines Ereignisses, so ist dieses Ereignis in der digitalen Aufzeichnung prinzipiell nicht rekonstruierbar. Beispiel: Sinussignal der Periodendauer 100 (Einheit beliebig, z.B. Millisekunde, Sekunde oder Jahrzent).
Periode=100; Dauer=600; Abtastintervall=1:

 
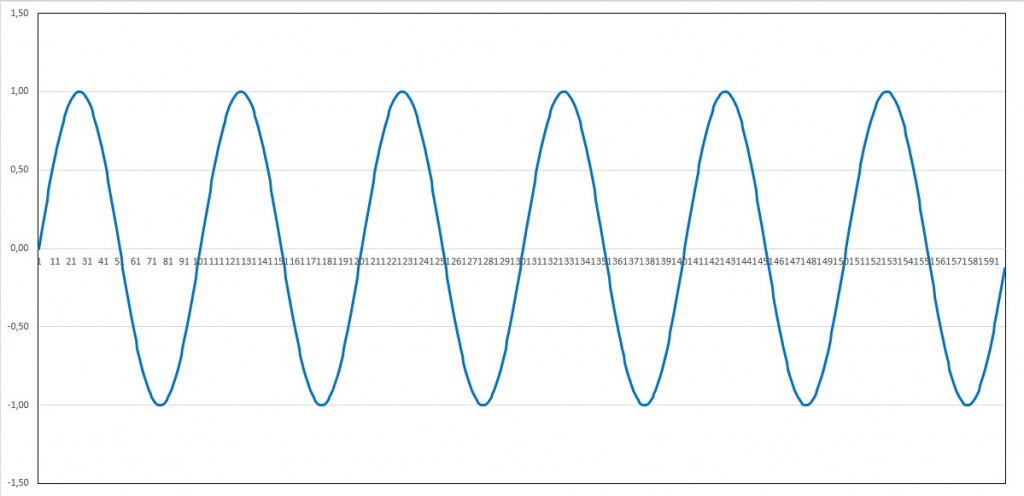
Bei einer Abtastschrittweite von einem Viertel der Periodendauer ist das Signal gut rekonstruierbar:
Periode=100; Dauer=600; Abtastintervall=25:

 
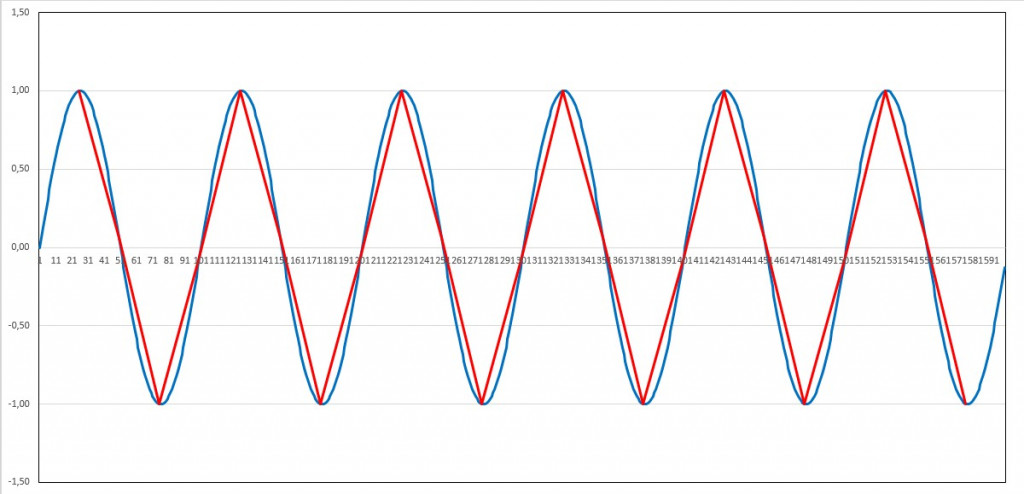
Auch mit einer Abtastschrittweite von einem Drittel der Periodendauer ist die Periodizität gut nachweisbar:
Periode=100; Dauer=600; Abtastintervall=33:

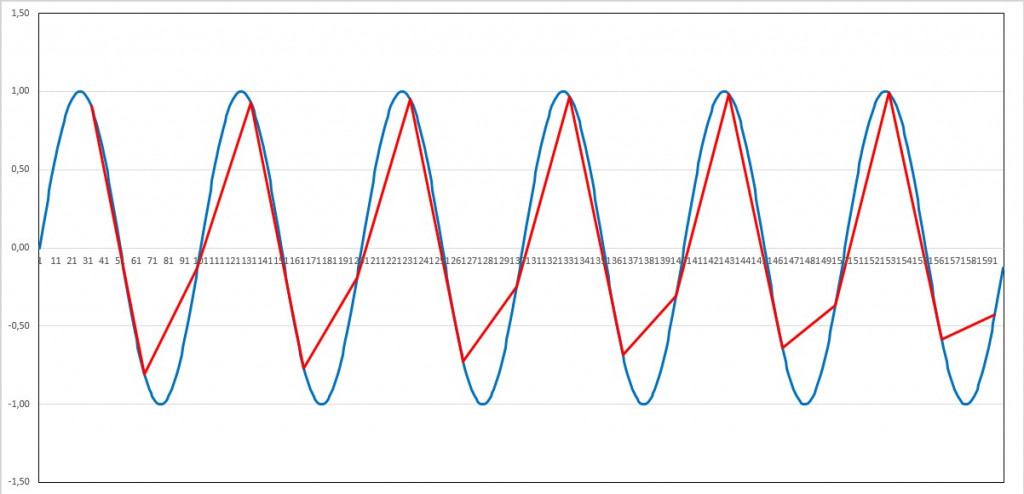
Bei einer Abtastschrittweite minimal kürzer als die Hälfte der Periodendauer sind zwar die Amplituden stark verfälscht, ein Nachweis der Periodendauer gelingt dennoch.
Periode=100; Dauer=600; Abtastintervall=49:

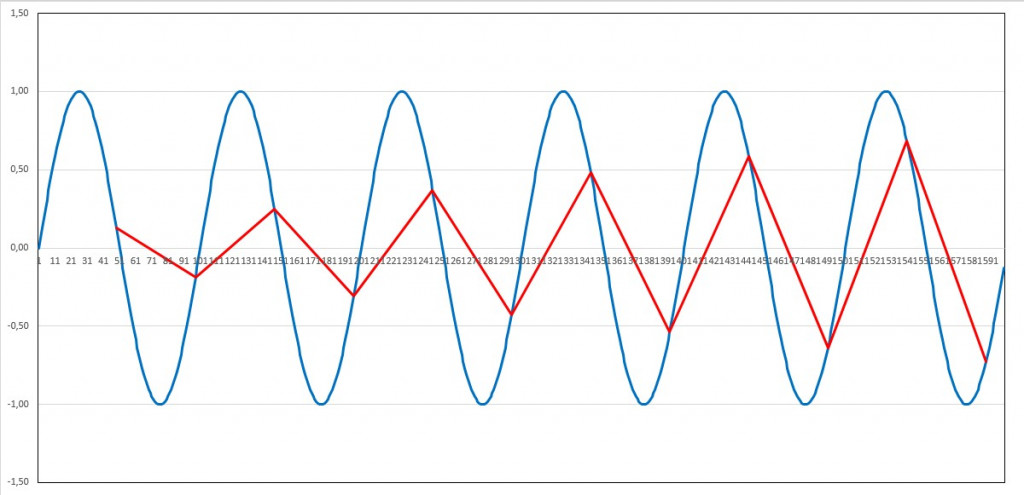
Bei einer gröberen Abtastung ist die Periodendauer nicht mehr nachweisbar. In dem abgetasteten Signal können sogar Schein-Frequenzen auftreten. Bei einer Abtastschrittweite von 2/3 der Periodendauer wird eine doppelt so große Periode (also halbe Frequenz) wie im ursprünglichen Signal „nachgewiesen“:
Periode=100; Dauer=600; Abtastintervall=67:

 
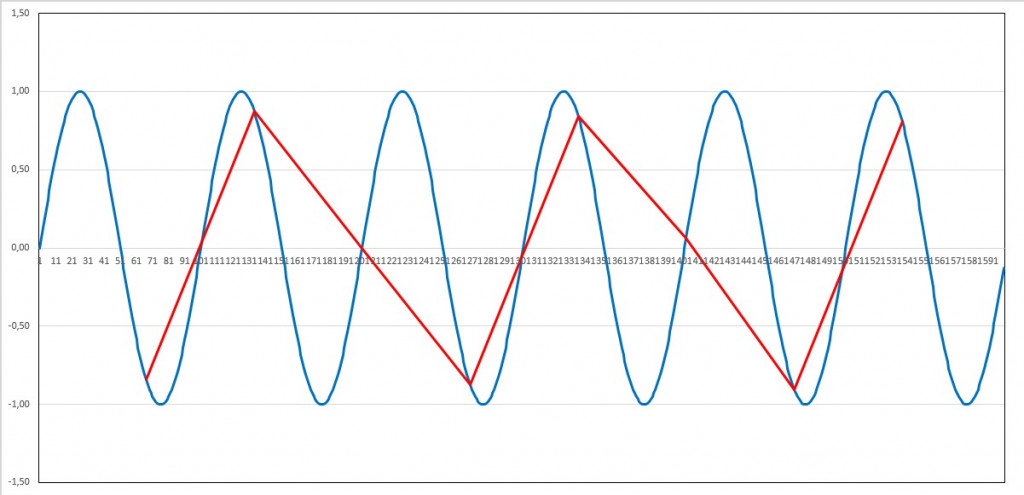
Bei einer Abtastung mit der Schrittweite von ¾ der Signalperiode entsteht eine Schein-Periode der 3-fachen Dauer:
Periode=100; Dauer=600; Abtastintervall=75:

 
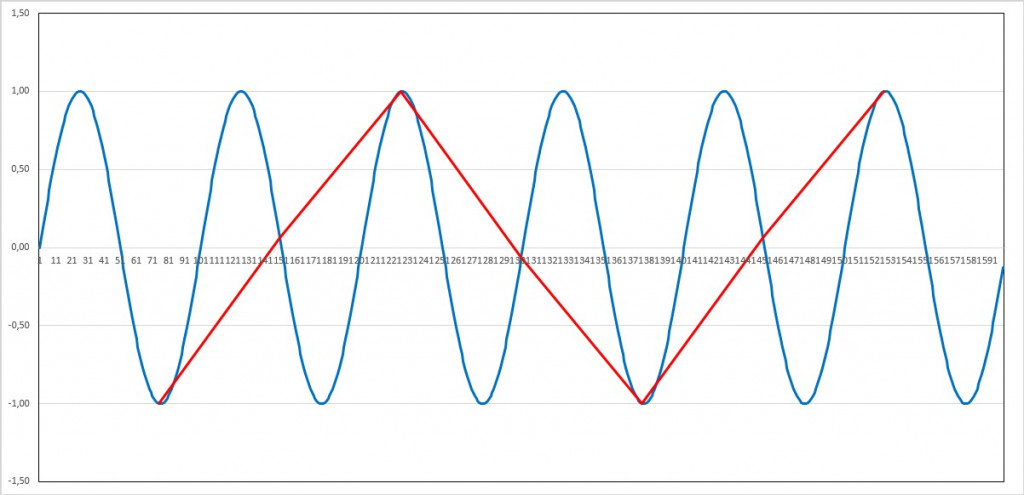
Dieser Effekt wird „Aliasing“ genannt.
Fassen wir zusammen:
Phänomene (d.h. Signale) einer bestimmten Dauer bzw. Periodizität können nur dann nachgewiesen werden, wenn deren Messung mit einer zeitlichen Auflösung von weniger als der halben Dauer erfolgt.
Paradebeispiele für die Verletzung dieses Prinzips sind die Publikation „A Reconstruction of Regional and Global Temperature for the Past 11,300 Years“ von Marcott et al. und deren Diskussion im Blog von Prof. Rahmstorf.
In der Arbeit wurde der regionale und globale Temperaturverlauf während des Holozäns untersucht. Dieser wurde anhand von Sedimentschichtungen bestimmt. Der Leitautor Marcott bemerkte hierzu:

„We showed that no temperature variability is preserved in our reconstruction at cycles shorter than 300 years, 50% is preserved at 1000-year time scales, and nearly all is preserved at 2000-year periods and longer“

Daraus ist zu schließen, dass die Abtastrate gröber als 150 Jahre war, in 50% der Fälle sogar zwischen als 500 und 1000 Jahren lag. Dies ist bemerkenswert, vergleichen die Autoren diesen rekonstruierten Temperaturverlauf doch mit dem Temperaturverlauf einiger Jahrzehnte des 20. Jahrhunderts, dessen zeitliche Auflösung typischerweise bei einem Monat liegt. Dazu schreibt Prof. Rahmstorf:

„Entscheidend ist vielmehr, dass der rasche Anstieg im 20. Jahrhundert im ganzen Holozän einmalig ist.“

Diese Behauptung ist wissenschaftlich nicht haltbar, da aufgrund der geringen zeitlichen Auflösung der Sedimentdaten ein potentieller abrupter Temperaturanstieg analog zum 20. Jahrhundert prinzipiell nicht nachweisbar ist. Sedimentdaten sind für eine solche Analyse ungeeignet.
Eine Grafik wie in Abb. 1 von Rahmstorfs Diskussion stellt wegen massiv unterschiedlicher zeitlicher Auflösung keinen seriösen Vergleich zweier Messreihen dar und dient eigentlich nur zur Stimmungsmache.
 
Merke:
Immer dann, wenn behauptet wird, dass augenblickliche Veränderungen oder Trends einmalig in der Geschichte seien, sollte man sehr genau hinschauen, mit welchen historischen Aufzeichnungen verglichen wird und ob ein solcher Vergleich überhaupt statthaft ist. Nicht immer werden Publikationen bzw. deren Schlussfolgerungen wissenschaftlichen Standards gerecht.
 

Untere Grenzfrequenz

Die untere Grenzfrequenz basiert auf der Gesamtdauer einer Messreihe. Eine solche Messreihe der Dauer T kann prinzipiell keine periodischen Vorgänge (bzw. Oszillationen) erfassen, deren Periodendauer größer ist als T. Dies bedeutet, dass zumindest eine volle Periode eines zyklischen Vorgangs in der Messreihe enthalten sein muss, um diesen zu erfassen. Wird eine Analyse über einen kürzeren Zeitraum durchgeführt, so wird diese Periode nicht zu erkennen sein. Beispiel: Sinussignal der Periodendauer 100 (Einheit beliebig, z.B. Millisekunde, Sekunde oder Jahrzehnt). Wird ein Signal der Periodendauer T hinreichend lange gemessen, d.h. die Messdauer beträgt mindestens T, so lässt sich die Periode nachweisen:

 
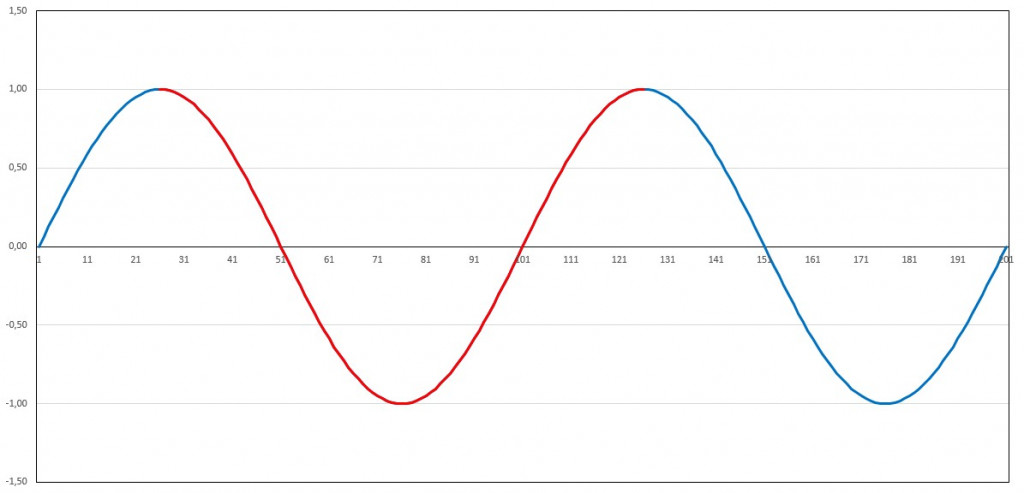
Ist die gesamte Messdauer kürzer, so lässt sich die Periodizität nicht rekonstruieren. Bei zu kurzer Messdauer können aus periodischen Vorgängen Schein-Trends ermittelt werden, die zu absurden Schlussfolgerungen führen. Erfolgt die Messung entlang des absteigenden Astes eines solchen Sinussignals, so ergibt sich – rein zufällig –  ein negativer Trend:

 
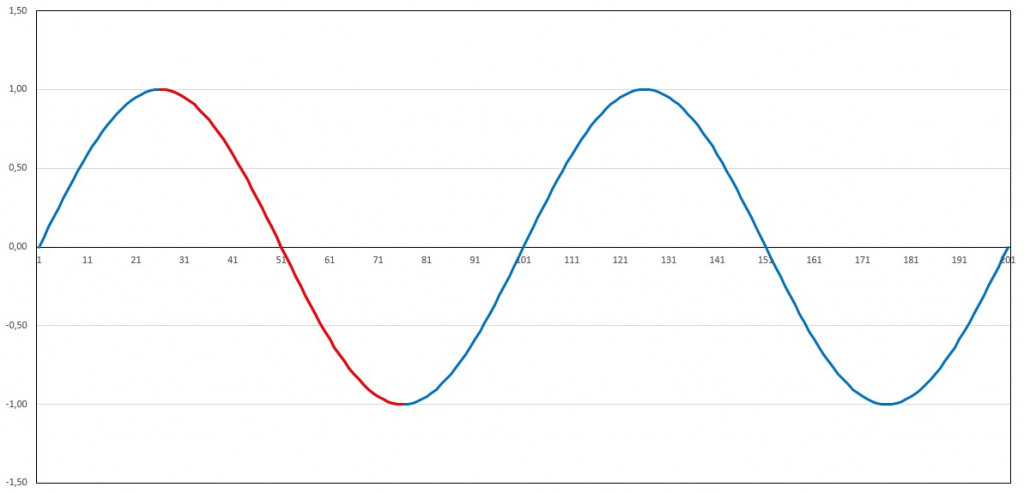
Bei einer Messung entlang des aufsteigenden Astes, wird – bei identischem Signal – ein positiver Trend ermittelt:

 
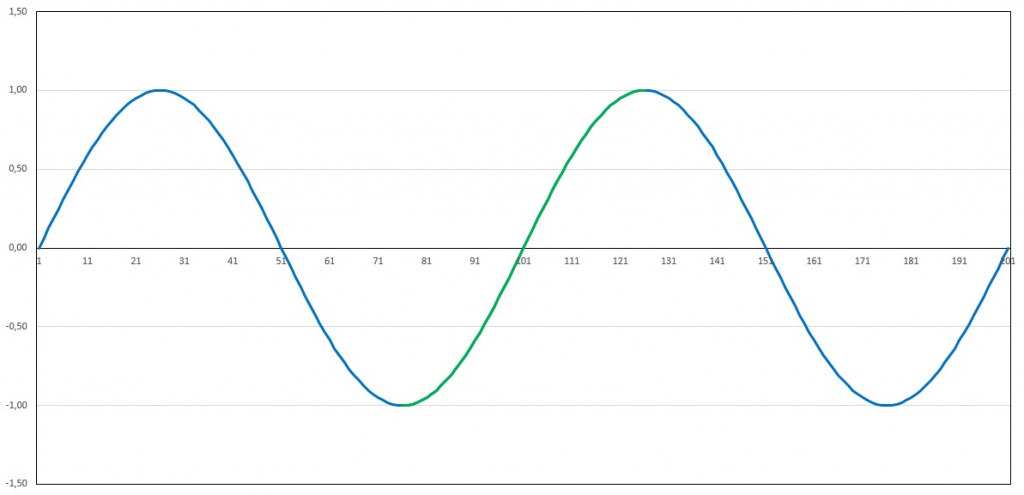
Es ist unschwer zu erkennen, dass die Ermittlung von Langzeittrends aus zu kurzen Messkampagnen zu unsinnigen Ergebnissen führt. Seit Ende der Kleinen Eiszeit ist ein Anstieg der globalen Temperatur zu verzeichnen. Dieser ist überlagert durch multidekadische Oszillationen mit Periodendauern von 50-70 Jahren (u.a. die Atlantische Multidekaden-Oszillation = AMO):

 
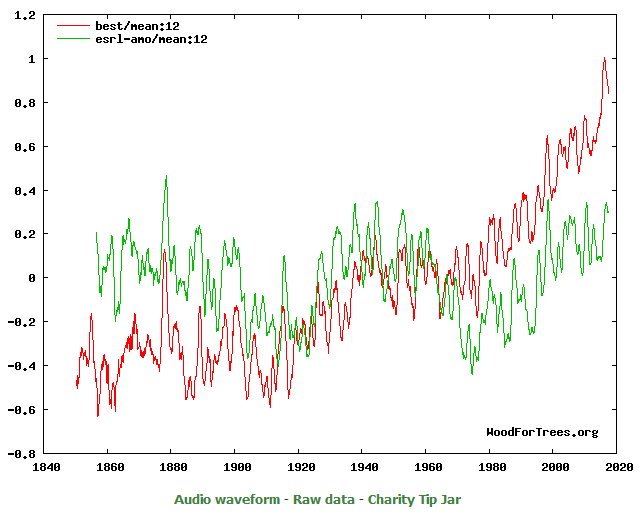
Quelle: http://woodfortrees.org/plot/best/mean:12/plot/esrl-amo/mean:12
Übertragen auf unser fiktives Beispiel erhalten wir folgende Grafik:

 
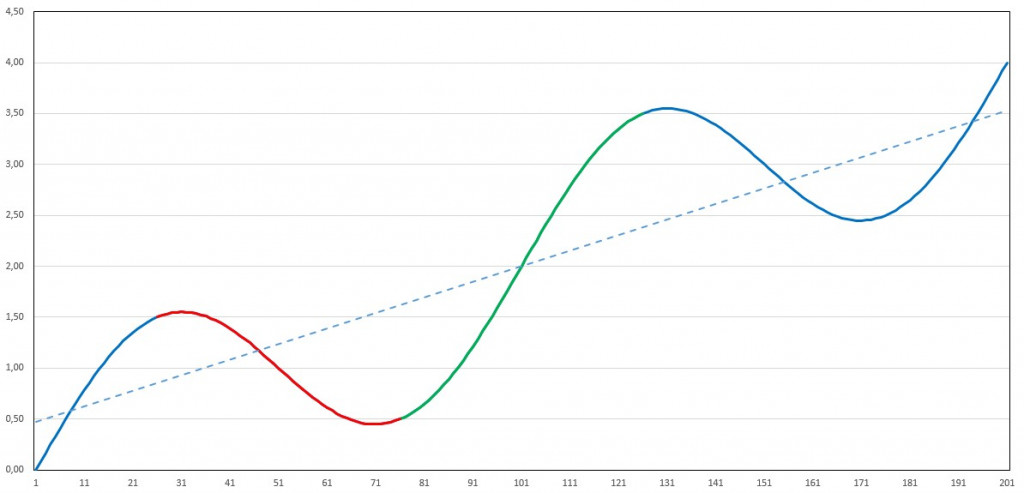
Erfasst die Messkampagne nur den absteigenden Ast der Oszillation (rote Teilkurve), so wird fälschlicherweise ein – wenn auch abgeschwächter – negativer Trend des gesamten Signals ermittelt. Bei Messung über den ansteigenden Ast (grüne Teilkurve) hinweg wird ein viel zu großer positiver Trend ermittelt.
Die Satellitenaufzeichnungen begannen 1979 bzw. 1980, dauern also bisher ca. 38 Jahre an. Dies ist etwa die halbe Periodendauer der Atlantischen Multidekaden-Oszillation. Zufälligerweise umfasst die Messdauer den ansteigenden Ast von AMO. Der seit Ende der Kleinen Eiszeit andauernde globale Temperaturanstieg wird in diesem Zeitraum durch diese ansteigende Phase verstärkt. Den daraus resultierenden Trend beispielsweise auf das Jahr 2100 zu extrapolieren, ist offensichtlich absurd. Aus der Analyse der Satellitendaten können multidekadische Oszillationen, deren Periode größer ist als 38 Jahre, prinzipiell nicht nachgewiesen und damit für Trendrechnungen auch nicht berücksichtigt werden.
Dass solche Analysen dennoch – entgegen der Prinzipien der Signalanalyse – durchgeführt werden, sieht man beispielsweise an der Publikation „Climate-change–driven accelerated sea-level rise detected in the altimeter era“ von Nerem et al.
Die Autoren unternehmen genau diese diskutierte Analyse für den Anstieg des Meeresspiegels, dessen Trend durch die ansteigende AMO-Phase verstärkt wurde. Dabei analysierten sie Satellitendaten, die bis 1993 zurückreichen, also über einen Zeitraum von lediglich 25 Jahren. Die daraus abgeleitete Prognose zum Meeresspiegelanstieg für das Jahr 2100 hält daher wissenschaftlichen Standards nicht stand. Ein anderes Beispiel für eine ungenügend lange Messdauer sind die Satellitenaufzeichnungen des arktischen Meereises, die ebenfalls seit 1979 stattfinden. Während der bisher 38-jährigen Analyse zeigte sich durchaus ein signifikanter Rückgang der eisbedeckten Fläche. Eine Extrapolation dieses negativen Trends in die Zukunft verbietet sich aber aus dem gleichen Grund.
Der Beitrag erschien zuerst bei Die Kalte Sonne hier