Experimentelle Verifikation des Treibhauseffektes Teil 1: Die gegenseitige Beeinflussung von Wolken und Treibhausgasen
Einführung
(an english version is provided hereEN – Experimental verification of the greenhouse effect)
Die ersten Erklärungsversuche des CO2-Treibhauseffektes wurden von der IR-Absorptions-Spektroskopie abgeleitet. Bei dieser Messmethode wird ein IR-Lichtstrahl aus einer Strahlungsquelle hoher Energiedichte durch eine mit CO2 gefüllte Küvette geleitet, wobei eine Schwächung seiner Intensität festgestellt wird. Dabei führt die von CO2 absorbierte Energie zu einer leichten Erwärmung der Küvette. Überträgt man diese Messmethode auf die Erde, ist die Erdoberfläche die Strahlungsquelle und die Atmosphäre ist die Küvette mit einem gewissen CO2-Gehalt.
In der Klimaforschung ist es üblich, die Atmosphäre als Ganzes zu betrachten und mit einem Emissions-Spektrometer von einem Satelliten (Upwelling Radiance, TOA = top of the atmosphere) die atmosphärische IR-Ausstrahlung zu messen. Bei der Interpretation dieser Spektren darf jedoch nicht übersehen werden, dass rund 60 % der Erdoberfläche von Wolken oder Dunst bedeckt sind und sie die größten Unsicherheiten bei der Klimamodellierung verursachen (1).
Wolken behindern die IR-Ausstrahlung der Erde durch Reflektion, Streuung, Absorption und Re-Emission. Zusätzlich können Energieströme durch Phasenübergänge (latente Wärme), Turbulenzen, Luftströmungen, Fall- und Aufwinde beeinflusst werden. Eine Laborapparatur wird all diese Einflussgrößen nicht simulieren können, sollte aber zumindest zwei Flächen mit verschiedenen Temperaturen, für die Erdoberfläche und für eine Wolkenschicht, enthalten. Einfache Vorrichtungen, die wie ein Gewächshaus von außen bestrahlt wurden, werden dieser Anforderung nicht gerecht. Transparente aber geschlossene Räume erwärmen sich bei Sonnenbestrahlung, weil sie hauptsächlich das Entweichen der erwärmten Innenluft verhindern (2), (3).
Eine Wolkenschicht ist in der Regel kälter als die Erdoberfläche und kann deswegen Energie von der Erde durch IR-Strahlung, Wärmeleitung, Konvektion und Evapotranspiration empfangen. Das neue Konzept zur Verifikation des Treibhauseffektes orientiert sich an der Energieübertragung, die durch IR-Strahlung erfolgt. Die Versuchsapparatur enthält als IR-Sender eine warme und als IR-Empfänger eine kalte Fläche mit den gleichen Temperaturen, die auch typisch für Erde und Wolken sind. In dieser ersten Mitteilung wird nur die IR-Strahlung von der kalten zu der warmen Fläche untersucht. Da diese Strahlungsrichtung dem vorherrschenden Energietransport von warm nach kalt widerspricht, wird sie auch als Gegenstrahlung bezeichnet. Die warme Fläche, Erd-Platte genannt, wird von dieser IR-Bestrahlung (Gegenstrahlung) beeinflusst und steht im Mittelpunkt der Untersuchung. Die Apparatur simuliert eine Erdoberfläche unter Wolken und kann somit als ein Modell der erdnahen Atmosphäre betrachtet werden. Wird die Röhre mit IR-aktiven Gasen gefüllt, kann ein möglicher Treibhauseffekt dieser Gase unter naturnahen Bedingungen untersucht werden.
Eine völlig andere Methode zum experimentellen Nachweis des Treibhauseffektes geht vom Aufbau eines IR-Spektrometers aus (4). Schon der Titel „Absorption thermischer Strahlung durch atmosphärische Gase“ verrät, dass hier nicht die IR-Strahlung, sondern nur die Absorption der Treibhausgase studiert wird, die durch eine Erwärmung charakterisiert ist. Diese bei vielen Experimenten beobachtete Erwärmung CO2-haltiger Luft war ursprünglich eine „einfache“ Erklärung für die relativ hohen Erd-Temperaturen. Das hat sich allerdings weitgehend gewandelt. Die Erkenntnis, dass der größte Teil der IR-Ausstrahlung in das Weltall nicht von der Erdoberfläche, sondern von der Atmosphäre ausgeht, führte zu einem neuen Verständnis der Wärmeströme. Heutige Klimamodelle gehen von einer IR-Ausstrahlung von 240 W/m2 am Oberrand der Atmosphäre (TOA) aus (5). Nach dem IPCC hat CO2 diese Strahlungsbilanz beeinflusst, was als Strahlungsantrieb, eine von außen wirkende Kraft (radiative forcing, RF), bezeichnet wurde. Die Veränderung dieses Strahlungsantriebs dF wurde durch ein logarithmisches Verhältnis der CO2-Konzentration C (in ppm) zu einer vorindustriellen Konzentration C0 von 280 ppm beschrieben.
Gleichung 1: CO2-Strahlungsantrieb: dF = 5,35 ∙ ln(C/C0) W/m2
Nach der differentiellen Form des Stefan-Boltzmann Gesetzes (dT = dS/S/4 ∙ T) errechnet sich eine Temperaturerhöhung von 1,11 K pro CO2-Verdoppelung (IPCC-Basiswert = CO2-Klimasensitivität), allerdings ohne Berücksichtigung von Wolken, Wasserdampf und Rückkopplungen (6).
Gleichung 2: CO2-Klimasensitivität: dT = 5,35 ∙ ln(2)/240/4 ∙ 288 = 1 ,11 K
NASA-Satelliten messen oberhalb der Atmosphäre (TOA) neben der IR-Strahlung von 240 W/m2 eine Sonnenreflektion von 101 W/m2 (= 30 % der 341 W/m2 Sonneneinstrahlung, Albedo=0,3). Diese Werte führten zu der These, dass eine Erde ohne Atmosphäre eine Temperatur von – 18 °C hätte (Abbildung 1, A) und angeblich durch Treibhausgase um 33 K auf eine Temperatur von + 15 °C erwärmt wird1.
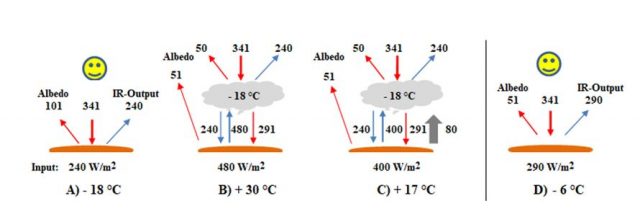
Abbildung 1: Energiebilanzen (W/m²) und Erd-Temperaturen (°C): Sonnenstrahlung (rot), IR-Strahlung (blau), Wasserverdunstung (grau) mit/ohne Wolken; Albedo 101 (A – C) bzw. 51 (D) W/m²
Eine Rechnung mit einem Schönheitsfehler, die „nackte“ Erdoberfläche hat nur eine Albedo von 0,15 = 51 W/m2 (7), (8), (9). Die 30%ige Reflektion (sphärische Albedo, gemessen vom Satelliten) wird nur zusammen mit den Wolken erreicht. Die Bezeichnung „Erde ohne Atmosphäre“ erweist sich als falsch und müsste korrekt „Erde mit Wolken“ heißen. Mit Hilfe der Wolken konnte man die Erd-Albedo (Erdkühlung) von 51 auf 101 W/m2 verdoppeln, wodurch der Erd-Input auf 240 W/m2 reduziert wurde und – 18 °C nach Fußnote 1 erhalten wird. Wenn man schon die „kalte“ Seite der Wolken in die Strahlungsrechnung mit aufnimmt, sollte man aber auch ihre IR-Emissionen, ihre erwärmende Seite, berücksichtigen. Ein Gedankenexperiment (Abbildung 1, B + C) zeigt, die Fragwürdigkeit eine „Erde mit Wolken, Albedo = 0,3“ berechnen zu wollen. Folgt man nur der Logik eines reinen Strahlungsaustausches nach Abbildung 1 B, so hätte eine Erde, die vollständig von Wolken bedeckt ist eine Temperatur von 30 °C (vorausgesetzt man billigt einer Wolkenschicht von -18 °C eine IR-Strahlung von 240 W/m2 zu, die sie in alle Richtungen gleichmäßig aussendet). Diese Rechnung ist unrealistisch, da sie als reine Strahlungsrechnung die Energieströme ignoriert, die zur Bildung von Wolken aber dazugehören. Ein realistischer Wert für eine „Erde mit Wolken“ wäre + 8 °C, wenn Wasserverdunstung und Wolkenbedeckungsgrad berücksichtigt werden2!
Die Strahlungsrechnungen offenbaren aber auch eine Überraschung! Wolken haben ein ähnliches Strahlungsverhalten wie Treibhausgase (9)! Sie lassen rund 85 % des Sonnenlichtes passieren (15 % werden reflektiert, Wolkenalbedo = 0,15; Absorption soll vernachlässigt werden, rote Pfeile), aber nicht das IR-Licht, das sie viel stärker absorbieren, streuen und emittieren (blaue Pfeile). Wolken und IR-Gase sind gemeinsame Komponenten des Treibhauseffektes mit vergleichbaren aber auch unterschiedlichen Eigenschaften. IR-Gase absorbieren nur bestimmte Wellenlängen des IR-Lichtes, dafür sind sie aber gleichmäßiger in der Atmosphäre verteilt. Wolken, die nur einen Teil der Erde bedecken, können jedoch als Schwarz-Strahler alle Wellenlängen des IR-Lichtes absorbieren. Im Unterschied zu IR-Gasen bewirken sie durch eine Reflektion der Sonnenstrahlen aber auch eine Kühlung der Erde, was ihre Beurteilung so schwierig macht.
Das Gedankenexperiment zeigt, dass für eine „Erde mit Wolken “ (Abbildung 1, B + C) verschiedene, aber vor allem sehr hohe Temperaturwerte erhalten werden. Die Rechnung nach Abbildung 1, A ist eine bewusste Täuschung der Öffentlichkeit mit der Absicht, den Treibhausgasen eine möglichst große Wirkung von 33 K zuzuschreiben.
Dabei wäre eine ehrliche, eindeutige Rechnung mit der „nackten Erde“ durchaus möglich gewesen, denn ihre Albedo = 0,15 (51 W/m2) ist bekannt (9) und hätte einen Temperaturbereich von – 3 °C (ε = 0,96) bis – 6 °C ergeben (ε = 1, Abbildung 1, D). Die tatsächliche, rund 20 K höhere Erd-Temperatur von + 15 °C ist die Folge verschiedener Einflussgrößen eines Wasserplaneten mit seinen Wolken, Treibhausgasen, seiner Wasserverdunstung und Strömungen der Atmosphäre. Der Beitrag der Treibhausgase an dieser Temperaturerhöhung ist noch zu bestimmen, ist aber auf jeden Fall deutlich kleiner als 20 K3.
Üblicherweise wird der CO2-Anstieg als Ursache und nicht als Folge einer Erderwärmung erklärt. Wird das aber in Fragegestellt, ergeben sich andere Interpretationen. So wurden auch Wolkenveränderungen durch kosmische Ereignisse als primäre Ursache von Temperaturschwankungen angenommen (10). Ebenfalls könnte auch ein geringerer, vom Menschen verursachter Wolkenbedeckungsgrad (Feinstaubminderung durch Rauchgasfilter) eine Erwärmung ausgelöst haben (11). In diesen Fällen wäre die CO2-Zunahme seit 1750 auch als Folge dieser Erderwärmung zu erklären.
Beschreibung des Versuchsaufbaus
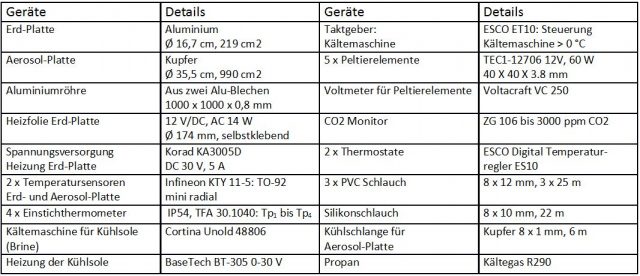
Die verwendete Apparatur besteht aus einer senkrecht stehenden Aluminiumröhre mit einem Volumen von 107 Litern und zwei domartigen Enden (Abbildung 2). In ihr befinden sich zwei 1,11 m entfernte Platten unterschiedlicher Temperatur. Die obere Platte (Erd-Platte) ist sowohl IR-Sender als auch Empfänger einer IR-Bestrahlung (Gegenstrahlung) und wird durch eine elektrische Heizfolie auf konstante 16,1 °C geregelt. Während eines Versuches wird die elektrische Leistung aufgezeichnet, die für eine konstante Temperatur der Erd-Platte benötigt wird.
Die untere Platte (Aerosol-Platte) kann durch eine integrierte Kühlschlange und ein externes Kälteaggregat bis -20 °C gekühlt werden. Diese Platte ist der Empfänger der IR-Ausstrahlung am Ende der Röhre und simuliert gleichzeitig die IR-Strahlung von Wolken/Aerosolen. Auf ihr befinden sich 5 Peltier-Elemente, die die IR-Ausstrahlung registrieren. Beide Platten besitzen einen Temperatursensor, dessen Werte über einen A/D-Wandler an einen Computer weitergeleitet werden.
Die warme und die kalte Fläche befinden sich in einer Aluminiumröhre, deren Wand zu einer dritten, unerwünschten Strahlungsfläche wird. Die Atmosphäre hat für diese Fläche keine Entsprechung. Dadurch entstand zunächst die Aufgabe, den Einfluss dieser Wand, ihre Wechselwirkung mit den anderen Strahlungsflächen zu verstehen, bevor mit den Messungen der IR-Gas-Strahlungen begonnen werden konnte. Aus Sicht der Erd-Platte ist die Wand der Aluminiumröhre ein Vordergrund-Strahler und die kalte Aerosol-Platte ist eine Wolkenschicht, die eine Hintergrund-Strahlung erzeugt.
Die Wand der Röhre und des oberen Doms ist mit Schläuchen umwickelt, die von zwei unabhängigen Thermostaten mit konstanter Wassertemperatur versorgt werden. Die Erd-Platte befindet sich dadurch in einer Wärmezone ähnlicher Temperaturen, die den körperlichen Wärmefluss von der Erd-Platte zu ihrer Umgebung minimiert. Die Temperatur des Innenraumes der Röhre wird alle 25 cm, beginnend mit Tp1 im oberen Dom, mit vier digitalen Einstichthermometern (Tp1 -Tp4) gemessen und wird manuell protokolliert. In diesem Bereich bildet sich von oben nach unten ein negativer Temperaturgradient von ca. 1 °C. Dadurch wird eine Thermik (Konvektion) der Innenluft in der senkrechtstehenden Apparatur verhindert.
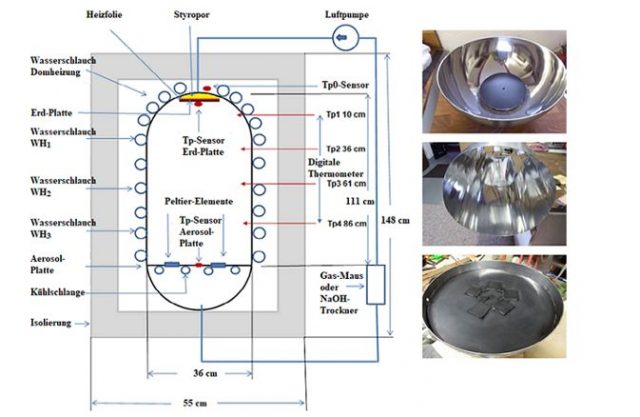
Abbildung 2: Links: Schematischer Aufbau des Experimentes; Rechts: von oben nach unten: Erd-Platte, Aluminiumröhre und Aerosol-Platte

Abbildung 3: Heizfolie unter der Erd-Platte; thermische Isolierung oberer Dom und Seitenwand; Schlauchumwicklung der Röhre
Das Strahlungsverhalten aller beteiligten Flächen
Der Innenraum der Versuchsapparatur enthält drei Flächen, Erd-Platte, Seitenwand und Aerosol-Platte, die IR-Strahlen aussenden können. Grundsätzlich gilt, dass jeder Punkt dieser Flächen IR-Strahlung in einem Raumwinkel von 0 – 180° aussendet1. Alle drei Flächen tauschen untereinander IR-Strahlen (Photonen) aus, wodurch Energie übertragen wird.
Abbildung 4 zeigt die Bestrahlung der Erd-Platte durch die Aerosol-Platte, wobei Erd-Platte und Wand immer die gleiche Temperatur haben. Die Aerosol-Platte ist ein Hintergrund-Strahler mit der IR-Ausstrahlung MH. Seine Photonen können die Erd-Platte auf direktem Wege oder durch (mehrfache) Reflektion an den verspiegelten Wandflächen erreichen. Ein Teil der HG-Strahlung MH wird jedoch von der Wand absorbiert (Strichlinie) und erreicht nicht die Erd-Platte. Die Aerosol-Platte trägt nur mit einem Teil ihrer Ausstrahlung MH zur Bestrahlung der Erd-Platte bei. Dieser Anteil wird effektive Hintergrund-Strahlung EH genannt.
In Abbildung 4 A ist die Aerosol-Platte (blau) kälter als die Wand (TpH < TpV). Die IR-Strahlung der Wand EV (roter Pfeil) ist größer als die absorbierte Energie von der Aerosol-Platte (blauer Strichpfeil). Die Wand ist hier ein Vordergrund-Strahler (Buchstabe „V“) und muss zusätzlich von außen geheizt werden (Wandheizung QV, Energie für den Vordergrund), um den Energieverlust auszugleichen2.
In Abbildung 4 B haben alle drei Flächen die gleiche Temperatur. Es gilt das Kirchhoffsche Gesetzt, wonach die absorbierte Strahlung der Aerosol-Platte (rot) und die emittierte Strahlung der Wand EV gleich groß sind. Die Bestrahlung der Erd-Platte durch die Aerosol-Platte wird de facto nicht behindert (adiabatischer Strahlungstransport). Die Wand benötigt keine Energiezufuhr, sie ist energetisch neutral.
Es soll die Energiebilanz der Erd-Platte ermittelt werden. Jeder feste (und flüssige) Körper mit einer Temperatur > 0 K sendet IR-Strahlen aus, die sich nach Stefan-Boltzmann berechnen lassen. Die IR-Ausstrahlung der Erd-Platte ME ist mit einem Energieverlust verbunden. Für eine konstante Temperatur muss der Erd-Platte die gleiche Energiemenge wieder zugeführt werden, die sie durch ihre IR-Emission verloren hat. Die Energiezufuhr erfolgt durch IR-Bestrahlung EG („G“ = Gegenstrahlung = Summe der IR-Strahlungen von Wand EV(Wand) und Aerosol-Platte EH) und Heizung der Erd-Platte QE (Gleichung 3).
Gleichung 3: Energiebilanz der Erd-Platte: ME = EG + QE; EG = EV(Wand) + EH ; ME = EV(Wand) + EH + QE
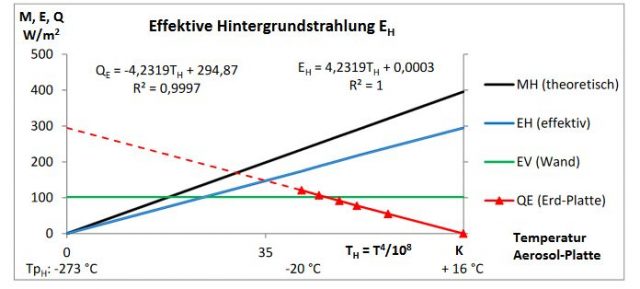
Die effektive Hintergrundstrahlung der Aerosol-Platte EH
Die Bestrahlung der Erd-Platte durch die Aerosol-Platte soll durch ein Abkühlungs-Experiment (Response-Versuch) untersucht werden.
Versuchsbeschreibung: Die Temperaturen der beiden Thermostate und des Kühlaggregates für die Aerosol-Platte wurden auf 16 °C eingestellt. Die Erd-Platte zeigte dabei eine Temperatur (TpE) von 16,09 °C an. Die elektrische Heizung QE (Indikator der Gegenstrahlung) und die elektrische Spannung der Peltier-Elemente UH (Indikator der Ausstrahlung der Röhre) waren nahezu Null. Danach wurde die Temperatur des Kühlaggregates in fünf Schritten auf -24 °C gesenkt, wodurch sich die Temperatur der Aerosol-Platte TpH auf -19,58 °C verringerte. Die Heizung der Erd-Platte QE musste kontinuierlich erhöht werden, um eine konstante Temperatur der Erd-Platte TpE sicherzustellen (Tabelle 1).
Tabelle 1: Response-Versuch (Nr. 145) ohne IR-Gase
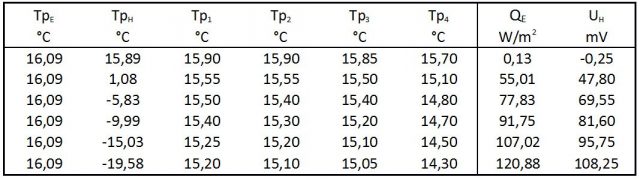
TpE, TpH = Temperaturen der Erd-, Aerosol-Platte und der Wandthermometer Tp1 bis Tp4
QE = Heizung der Erd-Platte, UH = Spannung, die von den Peltier-Elemente auf der Aerosol-Platte erzeugt wird
Auswertung (Abbildung 5): Die Temperatur der Aerosol-Platte wird als X-Achse in der Form von T4/108 aufgetragen6. Die theoretische IR-Ausstrahlung der Aerosol-Platte MH (schwarze Linie) wird nach dem Stefan-Boltzmann-Gesetz (ε = 1) berechnet. Beim Abkühlen der Aerosol-Platte von TpH = + 16 auf -20 °C wurde die elektrische Heizung QE(TH) fünfmal erhöht (rote Linie). Sollte die Aerosol-Platte weiter abgekühlt werden (rote Strichlinie), ließe sich aus der Trendlinie QE = -4,2319 ∙ TH + 294,87 die hierzu nötige Heizung der Erd-Platte QE berechnen. Bei TH = 0 K (absoluter Nullpunkt) müsste die Heizung QE demnach 295 W/m2 betragen. Da bei dieser Temperatur die Aerosol-Platte keine IR-Strahlung erzeugt, lässt sich nun Gleichung 3 in Gleichung 4 überführen und die Vordergrund-Strahlung der Wand EV zu 102,0 W/m2 (grüne Linie) berechnen. Dabei wurde eine IR-Ausstrahlung der Erd-Platte ME nach Stefan-Boltzmann zu 397 W/m2 zugrunde gelegt.
Gleichung 4: Strahlung der Wand EV (TH = 0 K): ME = EV + QE(TH=0)
EV = ME – QE(TH=0)
EV = 396,87 – 294,87 = 102,0 W/m2
Die effektive HG-Strahlung der Aerosol-Platte EH(TH) (blaue Linie) wird nach Gleichung 5 aus dem Anstieg der Trendlinie dQE/dTH berechnet.
Gleichung 5: Effektive HG-Strahlung EH(TH): ME = EH(TH) + EV + QE(TH)
EH(TH) = ME – EV – QE(TH)
EH(TH) = dQE /dTH ∙ TH
Von der theoretischen Ausstrahlung der Aerosol-Platte MH erhält die Erd-Platte nur einen gewissen Anteil EH (die effektive HG-Strahlung), da ein Teil der Photonen von der Wand absorbiert wird (schwarze vs. blaue Linie).
Das Experiment zeigt aber auch, dass die Erd-Platte von der Aerosol-Platte Energie EH erhält, obwohl letztere eine kleinere Temperatur TpH < TpE hat. Die Bestrahlung der Erd-Platte durch die Aerosol-Platte ist keine Verletzung des 2. Hauptsatzes der Thermodynamik, da letztlich der totale Wärmestrom weiterhin stets von der warmen Erd-Platte zur kalten Aerosol-Platte fließt, was an Heizung bzw. Kühlung beider Platten erkannt werden kann.
Es liegt in der Natur der „Response-Versuche“, dass die umgekehrte Strahlungsrichtung, die IR-Bestrahlung der Aerosol-Platte, nicht ausgewertet werden kann. Durch die schrittweise Abkühlung der Aerosol-Platte überlagern sich Bestrahlung und mechanische Wärmeströme (Diffusion und Wärmeleitung) und werden nur als Summe UH von den Peltier-Elementen auf der Aerosol-Platte angezeigt. Die Bestrahlung der Aerosol-Platte lässt sich jedoch ermitteln, wenn die Emissionsgrade von Treibhausgasen bei konstanten Temperaturen aller beteiligten Flächen bestimmt werden. Worüber gesondert berichtet werden soll.
Die effektive Hintergrundstrahlung EH in Gegenwart von Propan
Um die gemeinsame IR-Strahlung von Wolken und erdnahen IR-Gasen zu erforschen, wurden zwei Response-Versuche in Gegenwart von 1,3 bzw. 60 Vol.-% Propan (IR-aktives Modell-Gas) durchgeführt (Abbildung 6). In Gegenwart von Propan verringert sich die notwendige Heizung der Erd-Platte QE (rote Linien). Aus den beiden Trendlinien QE werden, wie im Kapitel Die effektive Hintergrundstrahlung der Aerosol-Platte EH beschrieben, die VG-Strahlung EV (grüne Linien, nach Gleichung 4) und die effektive HG-Strahlung der Aerosol-Platte EH (blaue Linien, nach Gleichung 5) erhalten.
Die Erhöhung der Propan-Konzentration verursacht gegenläufige Veränderungen. Einerseits erhöht sich die VG-Strahlung EV von 130 auf 272 W/m2 (grüne Linien)7, und andererseits verringert sich die effektive HG-Strahlung der Aerosol-Platte dEH/dTH von 3,88 auf 1,81 (blaue Linien). Propan absorbiert die Photonen der Aerosol-Platte (HG-Strahlung) und ersetzt sie durch eigene IR-Emissionen. Der tatsächliche Einfluss der Aerosol-Platte (blaue Linie) auf die Heizung der Erd-Platte QE verringert sich, obwohl ihre eigentliche Ausstrahlung MH (schwarze Linie) unverändert ist. Aus Sicht der Erd-Platte wird die Hintergrund- von der Vordergrund-Strahlung des Propans verdeckt.
Dieses Phänomen ist die Ursache, dass der Weltklimarat glaubt, dass der Beitrag der Wolken zum erdnahen Treibhauseffekt nur 30 W/m2 beträgt (9). Dabei wurde die tatsächliche, fast zehnmal stärkere HG-Strahlung der Wolken MH übersehen. Das hat letztlich dazu geführt, dass die Relativierung des Treibhauseffektes durch Wolken nicht erforscht wurde8.
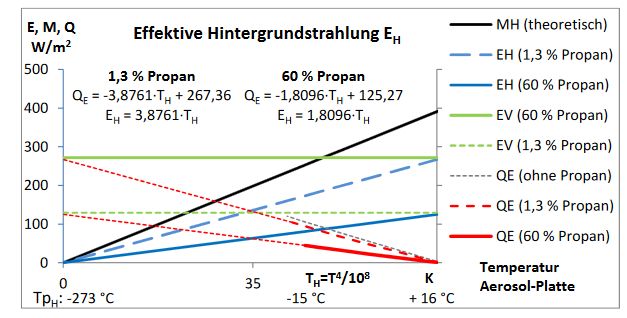
Abbildung 6: Verringerung der effektiven HG-Strahlung der Aerosol-Platte E<sub>H</sub> durch Propan
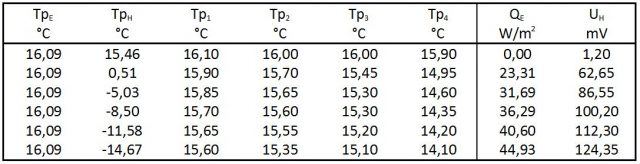
Tabelle 2: Response-Versuch (Nr. 212) in 1,3 Vol.-% Propan
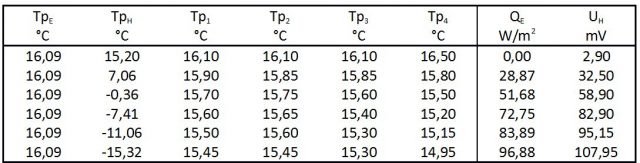
Tabelle 3: Response-Versuch (Nr. 156) in 60 Vol.-% Propan
Die Relativierung der Propan-Strahlung
Die gemeinsame Bestrahlung der Erd-Platte EG von nunmehr drei Strahlungsquellen (Wand, Propan und Aerosol-Platte) ergibt sich aus der Summe der beiden VG-Strahler (EV(Wand) und EV(Propan)) und der effektiven HG-Strahlung der Aerosol-Platte EH(TH) (Gleichung 6).
Gleichung 6: Bestrahlung der Erd-Platte EG: EG = EV(Wand) + EV(Propan) + EH(TH)
Durch die zusätzliche VG-Strahlung des Propans EV(Propan) erhöht sich die Bestrahlung der Erd-Platte EG (Abbildung 7, rote Linien), wodurch sich die Strahlungskühlung der Erd-Platte PE (die Differenz von ihrer IR-Ausstrahlung ME und ihrer IR-Bestrahlung EG) verringert (Gleichung 7).
Gleichung 7: Strahlungskühlung PE: PE = ME – EG
Setzt man in Gleichung 7 für ME den Ausdruck EG + QE (aus Gleichung 3) ein erhält man Gleichung 8.
Gleichung 8: PE = EG + QE – EG; => PE = QE
Die Übereinstimmung von Strahlungskühlung PE und Wärmezufuhr QE ist ein grundlegendes Prinzip für den Gleichgewichtszustand einer warmen Fläche, die IR-Strahlung abgibt. Eine Fläche kann im Gleichgewicht nur so viel Energie durch IR-Strahlung abgeben wie ihr auf anderem Wege zugeführt wird (PE = QE). Verringert sich die Strahlungskühlung PE (wie bei den Propan-Versuchen) muss für eine konstante Temperatur der Erd-Platte die Wärmezufuhr QE adäquat verringert werden.
Setzt man aber bei der realen Erde eine konstante Wärmezufuhr QE durch Sonneneinstrahlung voraus, würde eine stärkere Bestrahlung der Erdoberfläche EG (durch Treibhausgase) zunächst PE verkleinern. Die Erde müsste sich erwärmen um nach Gleichung 7 durch einen Anstieg der Erd-Ausstrahlung ME die Gleichheit von PE und QE wieder herzustellen9.
Mit dem Propan-Versuch wurde somit nachgewiesen, dass IR-aktive Gase die Bestrahlung der Erdoberfläche EG erhöhen und grundsätzlich einen Treibhauseffekt haben, der die Strahlungskühlung PE beeinflusst.
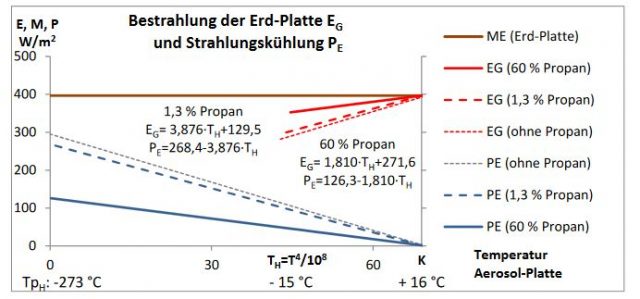
Abbildung 7: Verringerung der Strahlungskühlung PE (Treibhauseffekt) durch Propan
Abbildung 7 zeigt, dass die Strahlungskühlung PE sowohl von der Propan-Konzentration als auch von der Temperatur der Aerosol-Platte abhängt. Daraus ergibt sich eine Relativierung (Abschwächung) des Propan-Treibhauseffektes, wenn die Temperatur der Aerosol-Platte TH berücksichtigt wird.
Bei der Aerosol-Platten-Temperatur TH = 0 K wird die Strahlungskühlung PE nur vom Propan und seiner Konzentration beeinflusst. Der Abstand der blauen Linien zur grauen Linie (PE ohne Propan) markiert bei dieser Temperatur den maximalen, theoretischen Treibhauseffekt des Propans. Mit zunehmender Temperatur der Aerosol-Platte TH verringert sich der reale Propan-Treibhauseffekt (die Abstände der Linien verkleinern sich). Bei TpH = 16 °C ist die Strahlungskühlung PE bei allen Versuchen null, unabhängig ob Propan vorhanden ist oder nicht. Erd- und Aerosol-Platte haben hier die gleiche Temperatur, und die von Propan absorbierte und emittierte Energie ist gleich groß (adiabatischer Strahlungstransport, siehe auch Abbildung 4, B).
Tabelle 4 zeigt diese Verringerung (Relativierung) des Treibhauseffektes10 als Faktor Feff, der aus dem Verhältnis des realen zum theoretischen Treibhauseffekt für beide Versuche errechnet wurde. Der Effektivitäts-Faktor Feff ist offensichtlich nicht von der Konzentration des Propans (seinem Treibhauseffekt), sondern nur von seiner Temperatur und der Hintergrund-Temperatur abhängig. Der reale Treibhauseffekt eines IR-aktiven Gases errechnet sich somit aus dem Strahlungsantrieb RF (seinem theoretischen Wert) durch Multiplikation mit dem Feff Faktor.
Tabelle 4: Verringerung des Propan-Treibhauseffektes in Abhängigkeit von der Temperatur der Aerosol-Platte TpH

Der erdnahe Treibhauseffekt hängt (wie beim Propan-Versuch) von einer HG-Strahlung, nämlich der IR-Strahlung der Wolken ab. Wolken bestehen aus Wassertropfen bzw. Eiskristallen, die wegen ihrer großen Oberfläche einem Schwarzstrahler nahe kommen, und wie die Aerosol-Platte die Wirkung der IR-aktiven Gase relativieren. Diese Relativierung des Treibhauseffektes durch Wolken wurde vom Weltklimarat bisher nicht berücksichtigt. Werden Wolken aber berücksichtigt, beträgt die reale CO2- Klimasensitivität nur rund 0,35 K, etwa ein Drittel des IPCC-Wertes von 1,11 K11.
Die Relativierung des Treibhauseffektes betrifft auch die Wasserdampf-Strahlung und damit die umstrittene CO2-Wasser-Rückkopplung. Hinzukommt, dass bei einer Erhöhung der Wolkenbedeckung (durch mehr Wasserdampf in der Atmosphäre) die Strahlung durch Wolken zunimmt, wodurch der Effektivitätsfaktor Feff kleiner wird.
Aber auch bei klarem Himmel ergibt sich eine unerwartete Abschwächung des Treibhauseffektes. Die Energie für die Propan-IR-Strahlung wird gemeinsam von der HG-Strahlung MH und der Wandheizung QV geliefert (Abbildung 4). QV ist ein verborgener Wärmestrom, der bei dem Experiment nicht quantifiziert wurde und mit abnehmender Temperatur der Aerosol-Platte ansteigt. Er lässt sich aber am Temperaturrückgang von Tp1 beim Abkühlen der Aerosol-Platte erkennen (Tabelle 2 und Tabelle 3). Bei der Erde bedeutet dieser Wärmestrom QV eine Zunahme der Konvektion von der Erdoberfläche zu den bodennahen IR-Gasen, wodurch die Erdoberfläche gekühlt wird.
Dass Wolken den erdnahen CO2-Treibhauseffekt verringern, ist keine neue Erkenntnis (1), (6), (12), (13) , (14). Auch direkte Messungen der atmosphärischen Gegenstrahlung in der Nähe von Barrow, Alaska (71.325 N, 156.615 W) bei verschiedenen Bewölkungsgraden zeigen diesen Zusammenhang (15).
Die Testung der Apparatur mit Propan zeigt, dass die Versuchsanordnung geeignet ist, das Strahlungsvermögen (Emissionsgrade) von Treibhausgasen aber auch ihre Relativierung (Abschwächung) durch eine HG-Strahlung zu bestimmen. Einzige Ausnahme ist die Wasserdampf-Strahlung, die mit dieser Apparatur nicht untersucht werden kann, da Wasserdampf auf der kalten Aerosol-Platte kondensieren bzw. gefrieren würde.
Zusammenfassung
Wolken und Treibhausgase tragen beide zum Treibhauseffekt der Atmosphäre mit ähnlichen aber auch unterschiedlichen Strahlungseigenschaften bei. In Gegenwart von Wolken kommt es zu einer Verstärkung der erdnahen Gegenstrahlung aber auch zu Überlagerungen. Einerseits verdecken die Treibhausgase den größten Teil der Wolken-Strahlung, aber andererseits relativieren Wolken die Wirkung der IR-aktiven Gase. Maßgeblich für die Abschwächung des Treibhauseffektes der IR-aktiven Gase sind Höhe (Temperatur) der Wolken und ihre optische Dichte.
Modell-Versuche mit Propan zeigen, dass sein tatsächlicher, realer Treibhauseffekt unter Wolken nur rund ein Drittel seines theoretischen Wertes betragen würde. Diese Relativierung, die alle Treibhausgase und auch die umstrittene CO2-Wasser-Rückkopplung betrifft, wurde vom Weltklimarat bisher nicht berücksichtigt, wodurch seine Berechnungen und Prognosen zu hoch ausfallen und korrigiert werden sollten.
Die Untersuchungen dienten der Testung einer neuen Apparatur, mit der die Strahlung der atmosphärischen Treibhausgase aber auch ihre Relativierung durch Wolken quantifiziert werden können.
Danksagung
Ich bin meiner Frau, Dr. Renate Schnell, für Geduld, Verständnis und Beistand zu großem Dank verpflichtet. Dipl.-Ing. Peter Dietze, Prof. Dr. Jörg Gloede, Dipl.-Ing. Michael Limburg, Prof. Dr. Horst-Joachim Lüdecke, Dr. Heinz Hug, Dr. Gerhard Stehlik, Dr. Fritz Theil danke ich für ihr Interesse, rege Diskussionen und wertvolle Hinweise.
Anhang
Literaturverzeichnis
1. Zellner, Reinhard. Klimaforschung, Die Fakten und ihre Wahrnehmung. Nachrichten aus der Chemie. 2017, Bde. 65, S. 662 – 666, Juni 2017.
2. Anthony Watts. Anthony Watts Thrashes Al Gore’s Climate Change Experiment. [Online] 20. 11 2011. [Zitat vom: 12. 01 2018.] https://shortlittlerebel.com/2011/10/20/anthony-watts-thrashes-al-gores-climate-change/.
3. Nahle, Nasif S. Repeatability of Professor Robert W. Wood’s 1909 experiment on the Hypothesis of the Greenhouse Effect. [Online] [Zitat vom: 14. 01 2018.] http://www.biocab.org/Experiment_on_Greenhouses__Effect.pdf.
4. Stephan Sirtl. Absorption thermischer Strahlung durch atmosphärische Gase. [Online] 12. 11 2010. [Zitat vom: 15. 01 2018.] http://hpfr03.physik.uni-freiburg.de/arbeiten/diplomarbeiten/sirtl_staatsexamen_2010.pdf.
5. Claußen, Martin. http://www.t-y-a.at/docs/070918_Absorptionsspektren-H2o+Co2.pdf. [Online] [Zitat vom: 01. 02 2018.]
6. Peter Dietze. Berechnung der CO2-Klimasensitivität. [Online] 19. 10 2016. [Zitat vom: 21. 01 2018.]
7. Schönwiese, Christian-Dietrich. Klimatologie. Stuttgart : Eugen Ulmer GmbH, 1994.
8. NASA. Measuring Earth’s Albedo. [Online] 21. 10 2014. [Zitat vom: 11. 02 2018.] https://earthobservatory.nasa.gov/IOTD/view.php?id=84499.
9. Wolken im Klimasystem. [Online] 08. 03 2018. [Zitat vom: 08. 03 2018.] http://wiki.bildungsserver.de/klimawandel/index.php/Wolken_im_Klimasystem.
10. Henrik Svensmark. [Online] 20. 02 2017. [Zitat vom: 24. 01 2018.] https://de.wikipedia.org/wiki/Henrik_Svensmark.
11. Graßl, Hartmut. Was stimmt? Klimawandel Die wichtigsten Antworten. Freiburg im Breisgau : Verlag Herder, 2007.
12. Moll, Udo. Klimawandel oder heisse Luft? Hamburg : Tredition GmbH, 2016.
13. Lindzen, Richard S. How Cold Would We Get Under CO2‐Less Skies? PhysicsToday. 1995, Bde. 48, 2, S. 78-80.
14. Wagner, Thomas. thomas.wagner@iup.uni-heidelberg.de. [Online] [Zitat vom: 13. 01 2018.] http://www.mpic.de/fileadmin/user_upload/pdf/Physik_der_Atmosphaere_Lecture_Wagner.pdf.
15. Christopher J. Cox, Penny M. Rowe, Steven P. Neshyba, and Von P. Walden. A synthetic data set of high-spectral-resolution infrared spectra for the Arctic atmosphere. [Online] Earth Syst. Sci. Data, 8, 199–211, 2016, 18. 01 2016. [Zitat vom: 23. 01 2018.] https://www.earth-syst-sci-data.net/8/199/2016/essd-8-199-2016.pdf.