Warnung: Dieser Beitrag enthält die Aussage Trends können keine zukünftigen Werte prognostizieren und tun es auch nicht. Wem dieser Gedanke zuwider ist, sollte jetzt aufhören zu lesen.

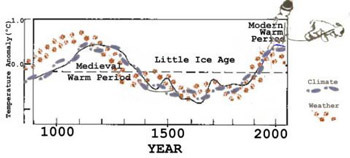
Ich beginne diesen Beitrag mit einem früheren Kommentar auf den ersten, oben verlinkten Beitrag von Andrew C. Rifkin mit dem Titel „Warming Trend and Variations on a Greenhouse-Heated Planet” vom 8. Dezember 2014. Darin verlinkt er auch meine Erwiderung. Der folgende Kommentar stammt von Dr. Eric Steig. Dieser ist Professor des Fachbereiches Earth & Space Sci. an der University of Washington, wo er als Direktor des IsoLab fungiert. Auf der Website der Fakultät wird er als Gründungsmitglied und Beitragender zu der einflussreichen (deren Bezeichnung) klimawissenschaftlichen Website RealClimate.org gelistet. Steig sagt:

Kip Hansens „Kritik“ des Cartoons ist clever – und geht vollständig an der Sache vorbei. Ja, die Kommentatoren hätten nicht sagen sollen, „der Trend bestimmt die Zukunft“, das war schlecht formuliert. Aber der Klima-Antrieb (zumeist CO2) bestimmt doch den Trend, und der Trend (wo Herrchen läuft) bestimmt, wohin der Hund gehen wird, im Mittel. (Hervorhebung von mir, Hansen)

Ich glaube, dass Dr. Steig seine Erwiderung einfach „schlecht formuliert“ hat. Er meinte sicherlich, dass die Klimaantriebe, welche selbst nach oben tendieren, die zukünftigen Temperaturen bestimmen („wohin der Hund laufen wird, im Mittel“). Diese Meinung steht ihm zu, aber er irrt sich, wenn er darauf besteht, dass „der Trend (wo Herrchen läuft) bestimmt, wohin der Hund läuft“. Es ist diese wiederholte und fast überall benutzte, ungenaue Wortwahl, welche einen erheblichen Teil der Missverständnisse auslöst sowie Schwierigkeiten in der englischsprachigen Welt (und ich vermute, auch in anderen Sprachen nach einer direkten Übersetzung), wenn es um Zahlen, Statistiken, Graphiken und Trendlinien geht. Menschen, Studenten, Journalisten, Leser, Publikum … fangen an, tatsächlich zu glauben, dass der Trend selbst zukünftige Werte bestimmt.

Viele werden nun sagen „Unsinn! Niemand glaubt so etwas!“ Das glaubte ich auch, aber man lese die Kommentare zu meinen beiden Beiträgen zuvor, und man wird erstaunt sein.

Datenpunkte, Linien und Graphiken:

Betrachten wir zunächst die Definition einer Trendlinie: „Eine Linie in einer Graphik, welche die allgemeine Richtung anzeigt, in die eine Gruppe von Datenpunkten zu laufen scheint“. Oder eine andere Version: „Eine Trendlinie (auch die Linie des besten Fits genannt) ist eine Linie, die man einer Graphik hinzufügt, um die allgemeine Richtung anzuzeigen, in welche die Punkte zu gehen scheinen“.

Hier folgt ein Beispiel (zumeist mit Bildern):

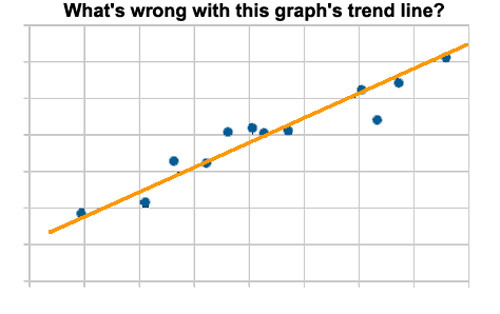
Trendlinien werden Graphiken bestehender Daten hinzugefügt, um die „allgemeine Richtung zu zeigen, in welche die Datenpunkte zu laufen scheinen“. Genauer, zur Klarstellung, die Trendlinie allein zeigt tatsächlich die allgemeine Richtung, in welche die Datenpunkte gelaufen sind – und man könnte hinzufügen „bisher jedenfalls“.

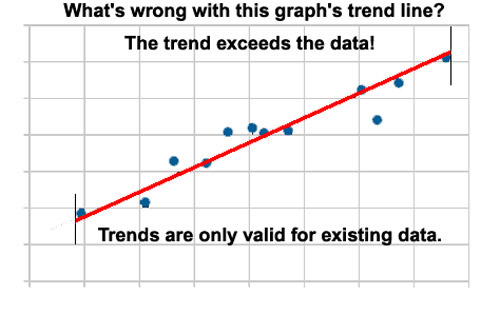
Das sieht sehr pingelig aus, oder? Aber es ist sehr wichtig für das Verständnis, was ein Datengraph wirklich ist – nämlich eine Visualisierung bestehender Daten – also der Daten, wie wir wirklich haben – und die gemessen sind. Wir würden alle zustimmen, dass die Hinzufügung von Datenpunkten an beiden Enden des Graphen betrügerisch ist – Daten, die wir gerade erst bekommen haben und die nicht wirklich gemessen oder experimentell gefunden worden sind. Aber trotzdem haben wir kaum jemanden gesehen, der gegen „Trendlinien“ ist, die weit über die auf dem Graphen liegenden Datenpunkte hinausgehen – gewöhnlich in beide Richtungen. Manchmal ist es Bequemlichkeit bei der Erstellung der Graphik. Manchmal liegt aber auch die absichtliche (ungerechtfertigte) Implikation zugrunde, dass Daten in Vergangenheit und Zukunft auf der Trendlinie liegen. Aber klar gesagt: falls es keine Daten „vorher“ und „nachher“ gibt, dann kann und sollte eine solche Hypothese nicht aufgestellt werden.

Hier noch ein oder zwei kleine Argumente:

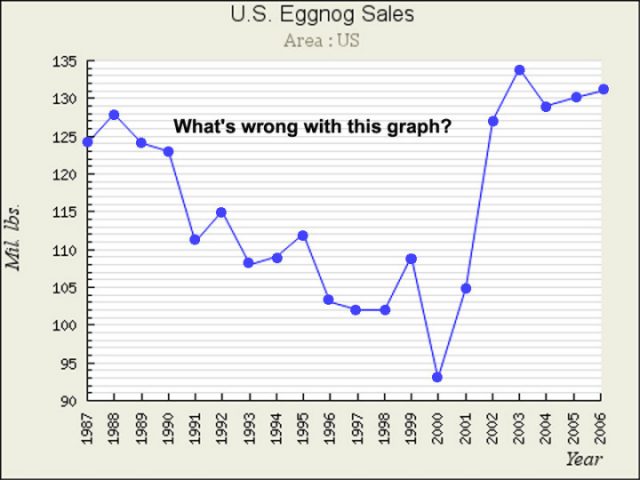
[Eggnog = Eierlikör]

Ich werde mit einer Graphik antworten:

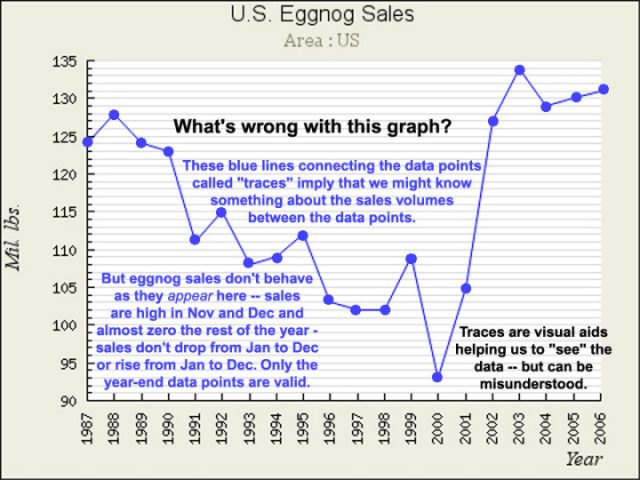
Aber (gibt es nicht immer ein ,Aber‘?):

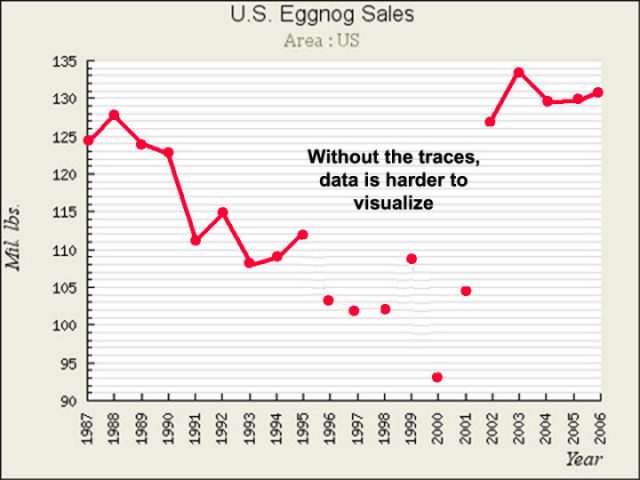
Fügt man den Datenpunkten auf einem Graphen Zwischenschritte hinzu, kann dies manchmal dazu führen, dass man diese Zwischenschritte als Daten ansieht, die zwischen den gezeigten Datenpunkten liegen. Angemessener würde der Graph NUR die Datenpunkte zeigen, falls das alles ist, was wir haben – aber wie oben gezeigt sind wir es nicht wirklich gewöhnt, Zeitreihen-Graphen auf diese Weise zu sehen – wir wollen die kleinen Linien über die Zeit laufen sehen, welche die Werte verbinden. Das ist gut, solange wir nicht auf den närrischen Gedanken kommen, dass die Linien irgendwelche Daten repräsentieren. Das ist nicht so, und man sollte sich nicht durch kleine Linien dazu bringen lassen zu glauben, dass zwischenzeitliche Daten sich entlang dieser kleinen Linien positionieren. Das kann so sein … oder auch nicht … aber es gibt keine Daten, zumindest nicht auf dem Graphen, die diesen Gedanken stützen.

Für Eierlikör-Verkäufe habe ich Teile des Graphen zwecks Anpassung an die Realität modifiziert:

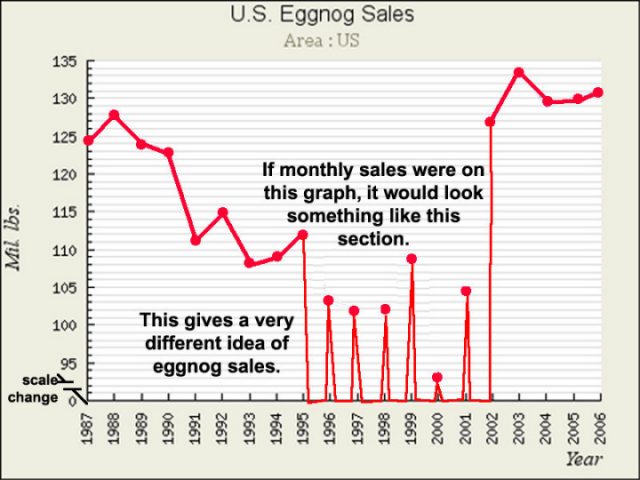
Dies ist einer der Gründe, warum Graphiken von so etwas wie „jährliche mittlere Daten“ erheblich irreführende Informationen vermitteln – die Spurlinien zwischen den jährlichen mittleren Datenpunkten können leicht dahingehend missverstanden werden, dass sie zeigen, wie sich die Daten in der dazwischen liegenden Zeit verhalten haben – zwischen year-end totals oder jährlichen Mittelwerten. Die graphische Darstellung jährlicher Mittelwerte oder globaler Mittelwerte verdeckt leicht wichtige Informationen über die Dynamik des Systems, welches die Daten hervorbringt. In einigen Fällen, wie Eierlikör wäre es sehr entmutigend, lediglich auf individuelle monatliche Verkaufszahlen zu schauen wie die Zahl der Verkäufe im Juli (die traditionell nahe Null liegen). So etwas könnte einen Eierlikör-Produzenten dazu verleiten, das jährliche Verkaufspotential erheblich zu unterschätzen.

Es gibt viele gute Informationsquellen, wie man eine Graphik angemessen anwendet – und über die allgemeinen Wege, auf denen Graphen missbraucht und missgebildet werden – entweder aus Ignoranz oder mit Absicht, um Propagandazwecke zu unterstützen. Sie treten fast überall auf, nicht nur in der Klimawissenschaft.

Hier folgen zwei klassische Beispiele:

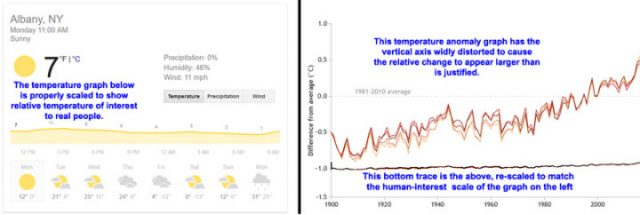
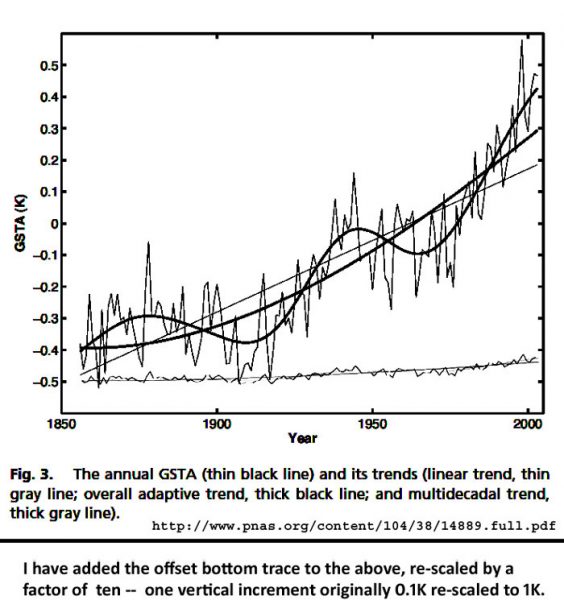
In beiden Graphiken gibt es noch ein weiteres, unsichtbares Element – Fehlerbalken (oder Vertrauensintervalle, wenn man so will) – unsichtbar, weil sie vollständig fehlen. In Wirklichkeit sind Werte vor 1990 „vage geraten“, Vertrauen nimmt von 1900 bis 1950 zu aufgrund von „Schätzungen [erraten] aus sehr ungenauen und räumlich sehr dünn verteilten Daten“. Vertrauen nimmt weiter zu von 1950 bis zu den neunziger Jahren aufgrund „besserer Schätzungen“ und schließlich in der Satelliten-Ära „bessere Schätzungen auf der Grundlage von rechenintensiver Hybris“.

Soweit die Einführung und die Beschreibung von Punkten, an die wir alle uns immer wieder mal erinnern sollten.

Der Knopf-Sammler [the button collector]: überarbeitet

Meine früheren beiden Beiträge über Trends konzentrierten sich auf den button collector, den ich hiermit noch einmal einführen möchte:

Ich habe einen Bekannten, der ein fanatischer Sammler von Knöpfen ist. Er sammelt Knöpfe bei jeder Gelegenheit, verwahrt sie, denkt jeden Tag an sie, liest über Knöpfe und Knöpfe sammeln; er bringt jeden Tag Stunden damit zu, seine Knöpfe in verschiedene kleine Schachteln zu sortieren und sorgt sich um die Sicherheit seiner Sammlung. Ich nenne ihn einfach den button collector*. Natürlich sammelt er nicht wirklich Knöpfe, sondern er sammelt Dollars, Yen, Lira, Pfund Sterling, Escudos, Pesos usw. Aber er verwendet sie nie für irgendeinen brauchbaren Zweck; sie helfen weder ihm noch anderen, also könnten es genauso gut auch Knöpfe sein.

[*Im Folgenden behalte ich den Begriff kursiv bei. Anm. d. Übers.]

Er hat nach der jüngsten Zählung Millionen über Millionen Knöpfe, genau, Sonntag Abend. Also können wir die „Millionen über Millionen“ ignorieren und einfach sagen, dass er Montag früh, zu Beginn seiner Woche, keine Knöpfe hat, um die Dinge vereinfacht darzustellen. (Man sieht schon, der Gedanke von „Anomalien“ hat schon ein paar Vorteile). Montag, Dienstag und Mittwoch gehen vorüber, und Mittwoch Abend zeigt ihm sein Buchhalter die folgende Graphik:

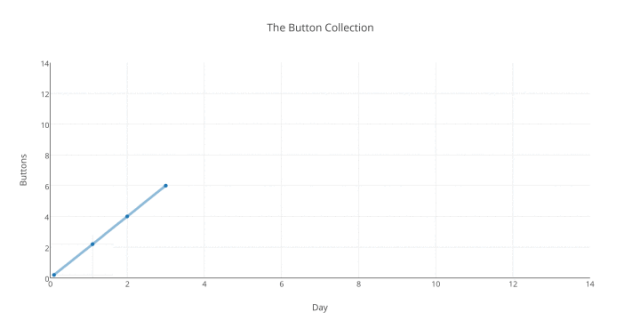
Wie in meinem Beitrag zuvor frage ich: „wie viele Knöpfe wird BC am Freitag Abend haben, also am Tag 5?“

Bevor wir antworten wollen wir darüber sprechen, was man tun muss, um diese Frage auch nur zu beantworten versuchen. Wir müssen einen Gedankengang formulieren, welches Verfahren mit diesem kleinen Datensatz modelliert wird. (Mit „modellieren“ meine ich einfach, dass die täglichen Ergebnisse irgendeines Systems visuell dargestellt werden).

„Nein, müssen wir nicht!“ werden Einige sagen. Wir nehmen einfach ein kleines Lineal zur Hand und zeichnen eine kleine Linie wie folgt (oder verwenden komplizierte mathematische Prozeduren auf unseren Laptops, die das für uns tun) und – voila! Die Antwort ist enthüllt:

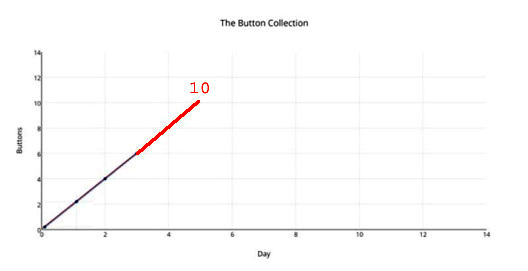
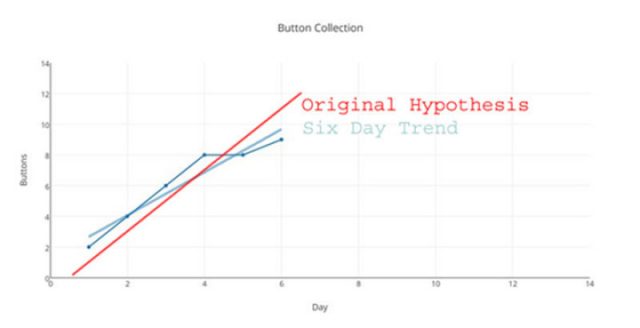
Und unsere Antwort lautet „10“ … … (und wird natürlich falsch sein).

Es gibt keinerlei mathematische oder statistische oder physikalische Gründe oder Rechtfertigung zu glauben, dass wir die korrekte Antwort gezeigt haben. Wir haben einen sehr wichtigen Schritt ausgelassen. Wir sind einfach zu schnell vorgegangen. Wir müssen zuerst versuchen zu ergründen, welcher Prozess dahinter steckt (mathematisch, welche Funktion hier graphisch dargestellt wird), der die Zahlen erzeugt, die wir sehen. Dieses Ergründen wird wissenschaftlicher eine „Hypothese“ genannt, ist aber an diesem Punkt nicht anders als jeder andere Guess. Wir können sicher annehmen, dass der Prozess (die Funktion) lautet, „der Gesamtwert von morgen wird der Gesamtwert von heute plus 2 sein“. Dies ist tatsächlich der einzige vernünftige Ansatz für die Daten der ersten drei Tage – und geht sogar konform mit formalen Prognose-Prinzipien (wenn man fast nichts weiß, prognostiziere man mehr des Gleichen).

Schauen wir mal auf den Donnerstag-Graphen:

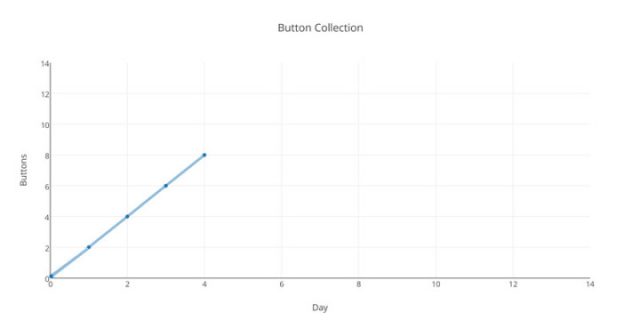
Klasse! Genau wie gedacht! Und jetzt Freitag:

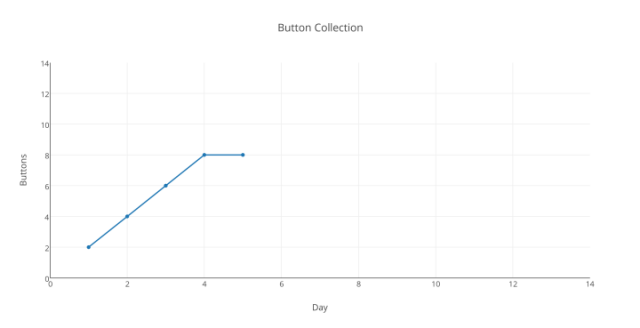
Hoppla! Was ist passiert? Unsere Hypothese ist mit Sicherheit korrekt. Vielleicht eine Störung…? Versuchen wir es mit Sonnabend (wir arbeiten über das Wochenende, um verlorene Zeit aufzuholen)

Aha, das sieht schon besser aus. Bewegen wir unsere kleine Trendlinie etwas, um sicher zu gehen…:

Na ja, sagen wir, immer noch ziemlich nah dran … jene verdammten Störungen!

Aber einen Moment … wie lautete unsere Original-Hypothese, unser guess hinsichtlich des Systems, des Prozesses, der Funktion, welche die Ergebnisse der ersten drei Tage ergab? Sie lautete „Die Gesamtzahl morgen ist die Gesamtzahl heute plus 2“. Stützen unsere Ergebnisse unsere Original-Hypothese, unseren first guess, bis zum Tag 6? (Klarstellung: diese Ergebnisse kommen einfach durch Zählen zustande – das ist unser Verfahren der Datengewinnung – zählen). Nein, tun sie nicht. Keine wie auch immer geartete Schummelei – etwa zu sagen „aufwärts ist aufwärts“ oder „der Trend ist immer noch steigend“ – lassen diese Ergebnisse unsere Hypothese stützen.

Was würde ein Wissenschaftler, der etwas auf sich hält, an diesem Punkt tun? Er darf viele Dinge nicht tun, als da wären: 1) Die Ergebnisse so frisieren, dass sie zur Hypothese passen, 2) so tun, als ob „nahe“ das Gleiche ist wie Unterstützung ist („erkennen Sie, wie eng die Trends korrelieren?“), 3) Die Option „warten wir bis morgen, wir sind uns sicher, dass sich die Störung aufklären wird“ übernehmen, 4) eine Neuzählung anordnen und sicherstellen, dass die Knopf-Zähler verstehen, welche Zahlen sie zu finden haben, 5) eine Re-Analyse durchzuführen, incremental hourly in-filling, krigging, de-trending and re-analysis and anything else, bis die Ergebnisse auf der Linie liegen, auf der sie „liegen sollten“.

Während unsere Kollegen diese Tricks durchführen, wollen wir schauen, was am Tag 7 passiert:

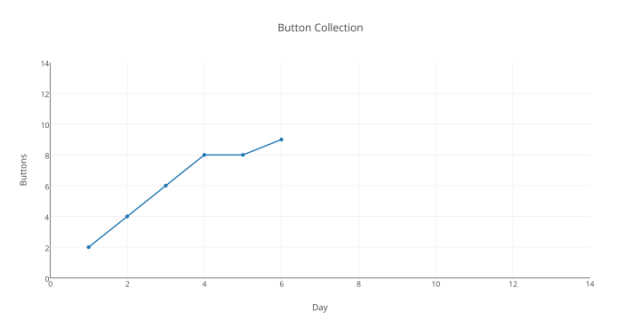
Oh Mann … mitten in unserem „immer noch steigend“-Mantra müssen wir erkennen, dass wir die Daten nicht mehr weiter verwenden können, um unsere Original-Hypothese zu stützen – irgendetwas Anderes, was wir nicht erwartet haben, muss hier geschehen sein.

Ein wahrer Wissenschaftler macht an diesem Punkt Folgendes:

Er stellt eine neue Hypothese auf, welche die tatsächlichen Ergebnisse besser erklärt, normalerweise mittels Modifizierung der Original-Hypothese.

Das ist schwer – erfordert es doch das Eingeständnis, dass man beim ersten Mal falsch gelegen hatte. Es kann bedeuten, einen wirklich schönen Gedanken aufzugeben – einen Gedanken, der professionell, politisch oder sozial ist, unabhängig davon, ob er die Frage, um die es hier geht, beantwortet. Aber – an diesem Punkt MUSS man das tun!

Tag 8, obwohl „in die richtige Richtung weisend“, hilft unserer Original-Hypothese auch nicht:

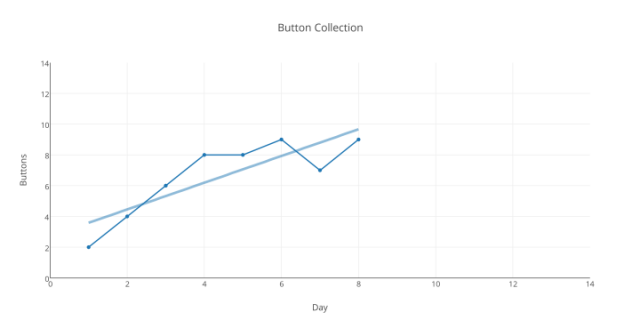
Der gesamte Trend der Woche „geht immer noch aufwärts“ – aber dafür ist eine Trendlinie nicht geeignet.

Warum also eine Trendlinie?

● Um uns zu helfen, das System oder den Prozess zu visualisieren und zu verstehen, der die Zahlen (tägliche Zählung der Knöpfe) hervorbringt (verursacht), die wir sehen – das ist vor allem nützlich bei Daten, die viel mehr durcheinander sind als hier.

● Um uns bei der Beurteilung zu helfen, ob die Hypothese korrekt ist oder nicht.

Solange wir nicht verstehen, was vor sich geht, welcher Prozess zugrunde liegt, werden wir kaum in der Lage sein, bedeutsame Prognosen abzugeben darüber, was die tägliche Zählung der Knöpfe in Zukunft ergibt. An diesem Punkt müssen wir einräumen, dass wir es nicht wissen, weil wir die zugrunde liegenden Prozesse nicht vollständig verstehen.

Trendlinien sind zum Austesten einer Hypothese sinnvoll. Sie können den Forschern visuell oder numerisch zeigen, ob sie einerseits das System oder den Prozess korrekt erkannt haben, welcher ihren Ergebnissen zugrunde liegt, oder ihnen andererseits aufzeigen, wo sie vom Weg abgekommen sind und ihnen Gelegenheit geben, Hypothesen umzuformulieren oder sogar „zurück auf Los gehen“, falls das notwendig ist.

Diskussion

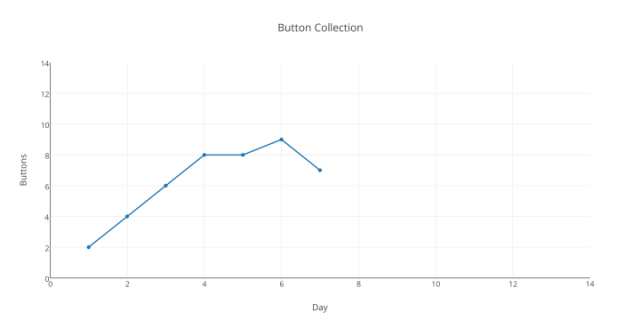
Mein Beispiel ist für die Leserschaft ein wenig unfair, weil es für Tag 10 keine offensichtliche Antwort auf die Frage gibt, die wir beantworten müssen: Welcher Prozess oder welche Funktion erzeugt diese Ergebnisse?

Das ist der ganze Punkt dieses Beitrags!

Ich will bekennen: Die Ergebnisse dieser Woche sind zufällig ausgesucht – es gibt kein zugrunde liegendes System, das es in den Ergebnissen zu entdecken gibt.

Derartiges tritt viel öfter bei Forschungsergebnissen auf als allgemein bekannt – man sieht scheinbar zufällige Ergebnisse, hervorgehend aus einer schlecht durchgeführten Studie, aus einer zu geringen Datenmenge, aus einer ungenauen Selektion der Parameter und einer „Hypothese weit daneben liegend“. Dies hat zu unsäglichen Bearbeitungen unschuldiger Daten geführt, die unablässig „bearbeitet werden, um Geheimnisse zu ergründen, die sie gar nicht enthalten“.

Wir glauben oft, dass wir ziemlich klar und offensichtlich sehen, was verschiedene Visualisierungen numerischer Ergebnisse uns sagen können. Wir kombinieren diese mit unserem Verständnis der Dinge, und wir geben kühne Statements ab, oftmals mit übertriebener Sicherheit. Haben wir diese erst einmal aufgestellt, sind wir versucht, aus falschem Stolz bei unseren first guesses zu bleiben. Falls unsere Zeiträume im obigen Beispiel nicht Tage, sondern Jahre gewesen wären, würde diese Versuchung sogar noch stärker sein, vielleicht unwiderstehlich – unwiderstehlich, falls wir zehn Jahre mit dem Versuch zugebracht haben zu zeigen, wie richtig unsere Hypothese ist, nur um zu sehen, dass die Daten uns betrügen.

Wenn unsere Hypothesen daran scheitern, die Daten zu prognostizieren oder zu erklären, die bei unseren Ergebnissen oder bei Messungen in Systemen der realen Welt zutage treten, brauchen wir neue Hypothesen – neue guesses – modifizierte guesses. Wir müssen uns dem Umstand stellen, dass unsere Hypothese nicht stimmt – oder noch schlimmer, dass sie vollständig falsch ist.

Von Linus Pauling, brillanter Chemiker und Nobelpreisträger, glaubt man allgemein, dass er sich zum Ende seines Lebens zu viele Jahre lang dem Kampf gegen eine Krebs-Kur mit Vitamin C verschrieben hat, und der es stets abgelehnt hat seine Hypothese neu zu evaluieren, als die Daten gegen sie sprachen und andere Gruppen seine Ergebnisse nicht nachvollziehen konnten. Dick Feynman machte für Derartiges etwas verantwortlich, dass er ,sich selbst zum Narren halten‘ nannte. Andererseits kann Pauling recht haben hinsichtlich der Fähigkeit von Vitamin C, gewöhnliche Erkältungen zu verhindern oder deren Dauer zu verkürzen. Dieses Thema war noch nicht ausreichend Gegenstand guter Experimente, um Schlussfolgerungen ziehen zu können.

Wenn unsere Hypothese nicht zu den Daten passt wie im oben ausführlich beschriebenen Beispiel – und es scheint dafür keine vernünftige, belastbare Antwort zu geben – dann müssen wir zurück zu den Grundlagen gehen und unsere Hypothesen testen:

1) Ist unser Experiment-Aufbau valide?

2) Sind unsere Messverfahren angemessen?

3) Haben wir die richtigen, zu messenden Parameter gewählt? Reflektieren/repräsentieren unsere gewählten Parameter (physisch) das, was wir glauben, dass sie reflektieren/repräsentieren?

4) Haben wir alle möglichen Störvariablen berücksichtigt? Sind die Störfaktoren um Größenordnungen größer als das, was wir zu messen versuchen? (Hier steht ein Beispiel).

5) Verstehen wir das größere Bild gut genug, um ein Experiment dieser Art angemessen durchzuführen?

Darum geht es heutzutage – das ist der Fragenkatalog, den ein Forscher aufstellen muss, wenn die Ergebnisse einfach nicht zur Hypothese passen, unabhängig von wiederholten Versuchen und Modifizierungen der Original-Hypothese.

„Moment“, kann man jetzt sagen, „was ist mit Trends und Prognosen?“

● Trends sind einfach nur graphische Visualisierungen der Änderungen während der Vergangenheit oder von vorhandenen Ergebnissen. Das möchte ich wiederholen: es sind Ergebnisse von Ergebnissen – Auswirkungen von Auswirkungen – es sind keine Ursachen und können auch keine sein.

● Wie wir oben sehen, können selbst offensichtliche Trends nicht herangezogen werden, um zukünftige Werte beim Fehlen eines wahren (oder zumindest „ziemlich wahren“) und klaren Verständnisses der Prozesse, Systeme und Funktionen (Ursachen) zu prognostizieren, welche zu den Ergebnissen, den Datenpunkten führen, welche die Grundlagen des Trends sind.

●  und falls man eine Größe verwendet, welche die Prozesse genau genug spiegelt, dann kann man dies heranziehen, um mögliche zukünftige Werte innerhalb bestimmter Grenzen zu prognostizieren – fast mit Sicherheit, falls Wahrscheinlichkeiten allein als Prognosen akzeptabel sind. Aber es ist das Verständnis des Prozesses, der Funktion, dass es gestattet, die Prognose abzugeben, nicht der Trend – und das tatsächliche kausative Agens ist immer der zugrunde liegende Prozess selbst.

● Falls man durch Umstände, Druck der Öffentlichkeit oder seitens der Politik oder einfach durch Hybris gezwungen wird, eine Prognose trotz des Fehlens von Verständnis abzugeben – mit großer Unsicherheit – ist es das Sicherste, „weiterhin das Gleiche“ zu prognostiziere und selbst bei einer solchen Prognose sehr viel Spielraum zuzulassen.

Anmerkungen:

Studien aus jüngerer Zeit zu Trends in nicht linearen Systemen (hier) geben nicht viel Hoffnung, abgeleitete Trends für Prognosen nutzen zu können. Meist reicht es nur zu „vielleicht wird es so weitergehen wie in der Vergangenheit – aber vielleicht wird es auch eine Änderung geben“. Klimaprozesse sind fast mit Sicherheit nicht linear – folglich ist es für Zahlen physikalischer Variablen als Ergebnis von Klimaprozessen (Temperatur, Niederschlag, atmosphärische Zirkulation, ENSO/AMO/PDO) unlogisch, wenn man davon gerade Linien (oder Kurven) über Graphiken numerischer Ergebnisse dieser nicht linearen Systeme zeichnet, um Projektionen zu erhalten und zu nicht physikalischen Schlussfolgerungen zu kommen.

Es gibt immer mehr Arbeiten zum Thema Prognose. (Hinweis: Die Konstruktion gerader Linien in Graphiken ist kein Beweis). Scott Armstrong bemühte sich viele Jahre lang, einen Satz von Prognose-Prinzipien zu entwickeln, um „wissenschaftliches Prognostizieren allen Forschern, Praktikanten, Klienten und Anderen zugänglich zu machen, die sich um Prognose-Genauigkeit kümmern“. Seine Arbeit findet sich hier. Auf seiner Website gibt es viele Beiträge zu Schwierigkeiten, Klima und globale Erwärmung zu prognostizieren (nach unten scrollen).

# # # # #

…

Der größte Teil der Leserschaft hier ist skeptisch hinsichtlich des Mainstreams und des IPCC-Konsens‘ der Klimawissenschaft, welche meiner Ansicht nach zu verzweifelten Versuchen verkommen ist, eine gescheiterte Hypothese namens „CO2-induzierte katastrophale globale Erwärmung“ mit aller Gewalt am Leben zu halten – Treibhausgase mögen allgemein eine gewisse Erwärmung bewirken, aber wie stark, wie schnell, wie lange sowie vorteilhaft oder schädlich – das sind alles Fragen, die bisher in keiner Weise beantwortet sind. Und außerdem steht immer noch die Frage im Raum, ob sich das Klima der Erde selbst reguliert trotz sich ändernder Konzentrationen von Treibhausgasen oder solarer Fluktuationen.

…

Link: https://wattsupwiththat.com/2018/01/04/the-button-collector-revisited-graphs-trends-and-hypotheses/

Übersetzt von Chris Frey EIKE