Delta T und Delta F
Aus einer Reihe von Gründen halte ich diese Theorie für äußerst zweifelhaft. Ich untersuchte das dieser Behauptung zugrunde liegende Problem für alle Interessierten mathematisch in einem Beitrag „The Cold Equations“. Heute spreche ich jedoch nicht über Theorie, sondern ich möchte einige der empirischen Daten unter die Lupe nehmen.
Der CERES-Datensatz enthält Messungen der Ausstrahlung an der TOA. Es gibt darin aber auch viele subsidiäre Datensätze, welche sowohl aus CERES-Daten als auch anderen Satellitendaten und Messungen am Boden berechnet werden. Darunter sind die ausgehende IR-Strahlung von der Erdoberfläche. Ich wende die Stefan-Boltzmann-Gleichung auf jene Daten der IR-Ausstrahlung an, um die Oberflächen-Daten zu berechnen. Diese Daten habe ich einem Vergleich mit den Temperaturdaten von HadCRUT unterzogen. Sie stimmten gut überein mit Ausnahme bestimmter Gebiete in der Nähe der Pole. Ich schreibe dies der sehr dünnen Bestückung mit Wetterstationen in diesen Gebieten zu. Daher wurden für diese Gebiete die Daten der nächst gelegenen Stationen extrapoliert. Aber selbst mit jener Differenz in den Polargebieten beträgt die Standardabweichung der Differenz zwischen CERES und HadCRUT bei den monatlichen Daten lediglich 0,08°C, ist also extrem gering. Die CERES-Daten sind vollständiger als die HadCRUT-Daten, weshalb ich erstere als Oberflächentemperatur heranzog.
Jetzt wollen wir Änderungen des Antriebs-Ungleichgewichtes an der TOA vergleichen mit Änderungen der Temperatur an der Erdoberfläche. Zu diesem Zweck müssen wir die Saison-Einflüsse entfernen. Dies tun wir, indem wir das Mittel des gesamten Datensatzes für jeden Monat von den Daten für jenen Monat subtrahieren. Für jeden Monat bleibt dann die „Anomalie“ übrig – um wie viel jener Monat wärmer oder kälter ist im Vergleich zum Mittel.
Beispielsweise sind hier die Temperaturdaten, wobei die obere Graphik die Rohdaten zeigt, die mittlere Graphik die jährlich sich wiederholenden jahreszeitlichen Variationen und die untere Graphik die „Anomalie“, um wie viel der Globus wärmer oder kälter ist im Vergleich mit dem Mittel.
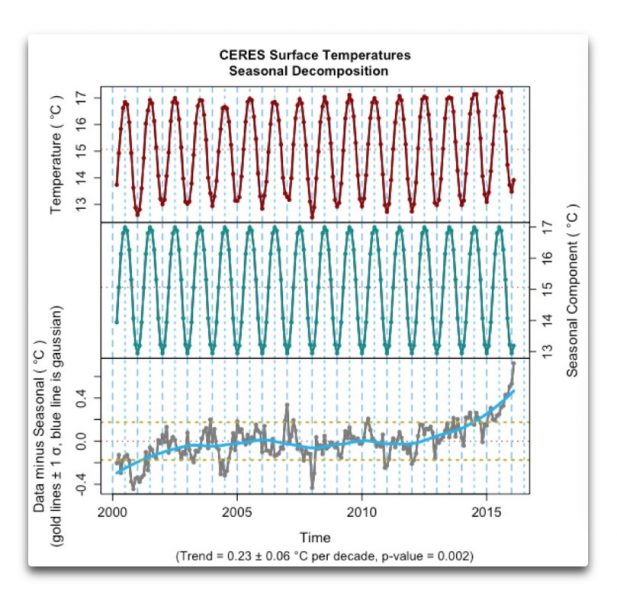
Abbildung 1: Rohdaten, jahreszeitliche Änderungen und Anomalie des CERES-Temperaturdatensatzes. Man beachte den Aufwärtstrend am Ende aufgrund des jüngsten El Nino. Seitdem ist es wieder kälter geworden, aber die CERES-Daten sind seit Februar 2016 nicht mehr aktualisiert worden.
Dem unrichtigen Paradigma zufolge, wonach Temperaturänderungen den Änderungen des Antriebs folgen, sollten wir eine Relation zwischen beiden in den CERES-Daten erkennen – wenn der Antrieb an der TOA einen großen Sprung macht, sollte dies auch die Temperatur tun, und umgekehrt. Allerdings zeigt sich, dass dies nicht der Fall ist:
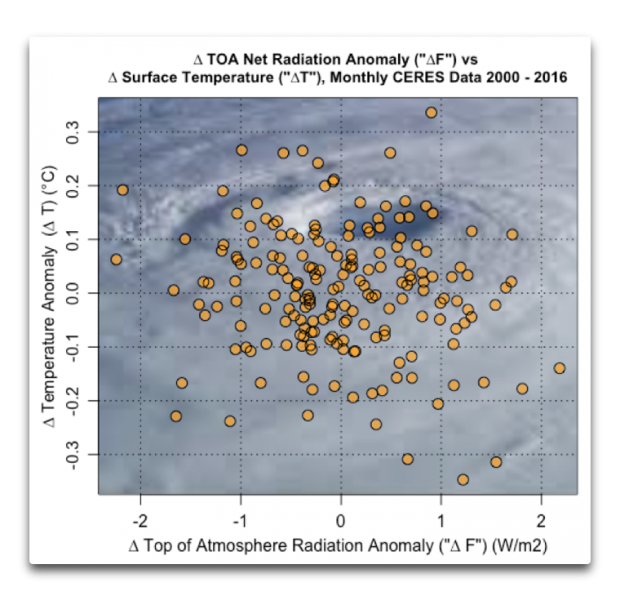
Abbildung 2: Änderungen der Strahlung an der TOA (Antrieb) ∆F vs. Änderungen der Temperatur am Boden ∆T. Delta (∆) ist das Standardsymbol für „Änderung“. In diesem Falle sind das die Änderungen von Monat zu Monat. Der Hintergrund ist ein Hurrikan aus Satellitenperspektive. Diesen habe ich hinzugefügt, weil ich des ewigen alten Weiß‘ überdrüssig bin.
Wie man leicht erkennt, gibt es im CERES-Datensatz keine statistisch signifikante Relation zwischen den Änderungen des Antriebs an der TOA ∆F und den Änderungen der Temperatur an der Oberfläche ∆T.
Nun höre ich jetzt schon einige Individuen etwas sagen wie „Aber Moment, das ist ein viel zu kurzer Zeitraum, um Auswirkungen so geringer Änderungen zu erkennen … also 1 W/m² über einen Monat? Die Erde weist thermische Trägheit auf, sie würde also gar nicht reagieren…“
Betrachten wir also einen anderen Scatterplot. Diesmal betrachten wir die Änderung der gesamt-Energieabsorption an der Erdoberfläche (kurz- und langwellig) im Vergleich zur Änderung der Temperatur.
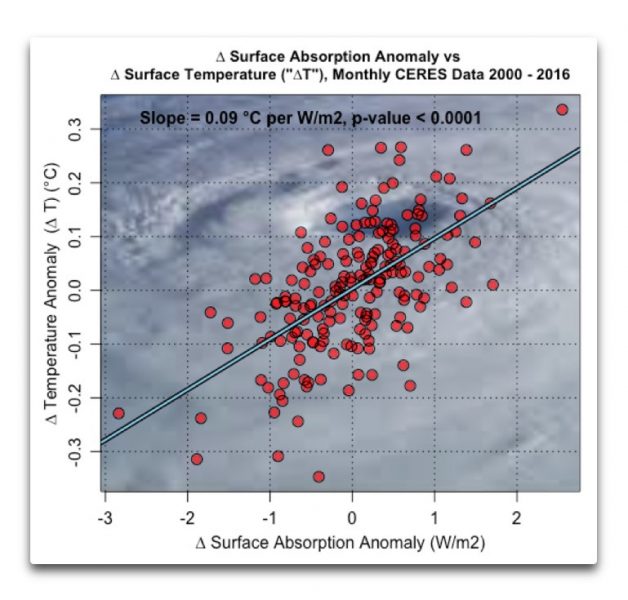
Abbildung 3: Änderungen der Energie-Absorption an der Oberfläche im Vergleich mit Änderungen der Temperatur an der Oberfläche ∆T.
Damit ist der Einwand der zu kurzen Zeitspanne annulliert. Eine Änderung von 1 W/m² über einen Monat ist in der Tat in der Lage, die Temperatur an der Oberfläche zu ändern, und zwar um ein Zehntelgrad.
Und schließlich: Ist dies lediglich ein Artefakt, weil wir CERES-Daten sowohl für die Temperatur als auch die Gesamt-Energieabsorption an der Oberfläche heranziehen? Dies können wir mittels Wiederholung der Analyse herausfinden, aber diesmal mit den HadCRUT-Daten anstatt der CERES-Daten …
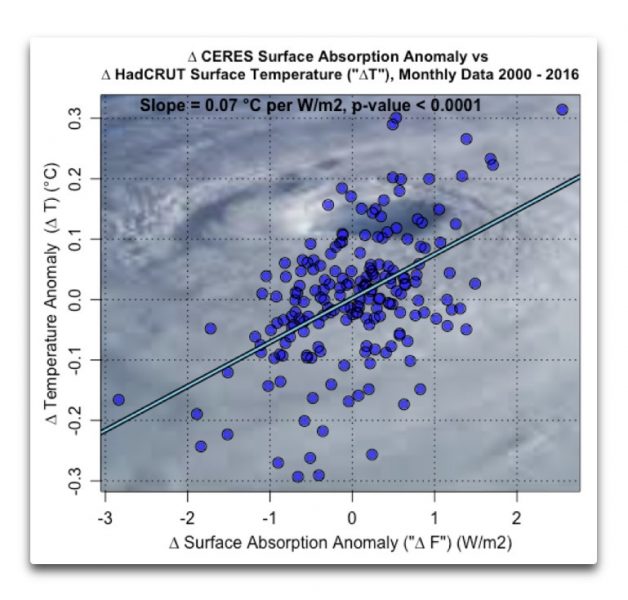
Wie wir erwartet haben, gibt es Differenzen bei der Verwendung unterschiedlicher Temperatur-Datensätze. In beiden ist die Oberfläche in der Lage, die Temperatur im Verlauf eines Monats aus einer Differenz von 1 W/m² heraus zu ändern.
Also bleiben wir zurück mit Abbildung 2: Sie zeigt, dass es keine signifikante Relation gibt zwischen Änderungen des Antriebs an der TOA und Temperaturen an der Erdoberfläche.
Man beachte, dass ich hier NICHT behaupte, dass man mit diesem Verfahren die so genannte „Klimasensitivität“ berechnen kann. Vielmehr weise ich lediglich darauf hin, dass die CERES-Daten nicht die erwartete Relation zwischen Änderungen des Strahlungs-Ungleichgewichtes an der TOA und Änderungen der Temperatur an der Erdoberfläche zeigen.
Link: https://wattsupwiththat.com/2017/12/18/delta-t-and-delta-f/
Übersetzt von Chris Frey EIKE